1. Computer Basics
Computers are useless. They can only give you answers.
1.1. Problem: Buying a computer
We begin almost every chapter of this book with a motivating problem. Why? Sometimes it helps to see how tools can be applied in order to see why they’re useful. As we move through each chapter, we cover background concepts needed to solve the problem in the Concepts section, the specific technical details (usually in the form of Java syntax) required in the Syntax section, and eventually the solution to the problem in the Solution sections. If you’re not interested in the problem, that’s fine! Feel free to skip ahead to Section 1.2 on hardware and software or to Section 1.3 on data representation, especially if you already have some programming experience. Then, if you’d like to see another detailed example, the solution to this problem is available in Section 1.4 as a reference.
We’ll start with a problem that’s not about programming and may be familiar to you. Imagine you’re just about to start college and need a computer. Should you buy a Mac or PC? What kind of computer is going to run programs faster? Do some kinds of computers crash more than others? Which features are worth paying more for? Why are there so many buzzwords and so much impenetrable jargon associated with buying a computer?
When many people hear “computer science,” these are often the first questions that come to mind. Most of this book is about programming computers in a language called Java and not about the computers themselves. We try to present all material so that almost any kind of computer can be used when programming the problems and examples. Nevertheless, both the hardware that makes up your computer and the other software running on it affect the way the programs you write work.
1.2. Concepts: Hardware and software
Computers are ubiquitous. We see them nearly everywhere. They are found in most homes, shops, cars, aircraft, phones, and inside many other devices. Sometimes they are obvious, like a laptop sitting on a desk, but most computers are hidden inside other devices such as a watch or a flat-panel television. Computers can be complex or relatively simple machines. Despite their diversity, we can think of all computers in terms of their hardware and the software that runs on it.
1.2.1. Hardware
Hardware consists of the physical components that make up a computer but not the programs or data stored on it. Hardware components can be seen and touched, if you are willing to open the computer case. One way to organize hardware is to break it down into three categories: the processor, the memory, and input and output (I/O) devices.
This view of a computer is a simplified version of what is called the von Neumann architecture or a stored-program computer. It’s a good (but imperfect) model of most modern computers. In this model, a program (a list of instructions) is stored in memory. The processor loads the program and performs the instructions, some of which require the processor to do a lot of number crunching. Sometimes the processor reads data out of memory or writes new data into it. Periodically, the processor may send output to one of the output devices or receive input from one of the input devices.
In other words, the processor thinks, the memory stores, and the I/O devices talk to the outside world. The processor sits between the memory and the I/O devices. Let’s examine these categories further.

CPU
The processor, or central processing unit (CPU), is the “brain” of a computer. It fetches instructions, decodes them, and executes them. It may send data to or from memory or I/O devices. The CPU on virtually all modern computers is a microprocessor, meaning that all the computation is done by an integrated circuit fabricated out of silicon. What are the important features of CPUs? How do we measure their speed and power?
| Frequency |
The speed of a CPU (and indeed a computer as a whole) is often quoted in gigahertz (GHz). Hertz (Hz) is a measurement of frequency. If something happens once per second, it has a frequency of exactly 1 Hz. Perhaps the second hand on your watch moves with a frequency of 1 Hz. In North America, the current in electrical outlets alternates with a frequency of approximately 60 Hz. Sound can also be measured by frequency. The lowest-pitched sound the human ear can hear is around 20 Hz. The highest-pitched sound is around 20,000 Hz. Such a sound pulses against your eardrum 20,000 times per second. That sounds like a lot, but many modern computers operate at a frequency of 1 to 4 gigahertz. The prefix “giga” means “billion.” So, we’re talking about computers doing something more than a billion (1,000,000,000) times per second. But what are they doing? This frequency is the clock rate, which marks how often a regular electrical signal passes through the CPU. On each tick, the CPU does some computation. How much? It depends. On some systems, simple instructions (like adding two numbers) can be computed in a single clock cycle. Other instructions can take ten or more clock cycles. Different processor designs can take different numbers of cycles to execute the same instructions. Instructions are also pipelined, meaning that one instruction is being executed while another one is being fetched from memory or decoded. Different processors can have different ways of optimizing this process. Because of these differences, the frequency of a processor as measured in gigahertz is not an accurate way to compare the effective speed of one processor to another, unless the two processors are very closely related. Even though it doesn’t really make sense, clock rate is commonly advertised as the speed of a computer. |
| Word size |
Perhaps you have heard of a 32-bit or 64-bit computer. As we discuss in the subsection about memory, a bit is a 0 or a 1, the smallest amount of information you can record. Most new laptop and desktop computers are 64-bit machines, meaning that they operate on 64 bits at a time and can use 64-bit values as memory addresses. The instructions that they execute often perform calculations on 64-bit quantities, i.e., numbers made up of 64 0s and 1s. The size of data that a computer can operate on with a single instruction is known as its word size. In day-to-day operations, word size is not important to most users. Certain programs that interact directly with the hardware, such as the operating system, may be affected by the word size. For example, most modern 32-bit operating systems are designed to run on a 64-bit processor, but most 64-bit operating systems do not run on a 32-bit processor. Programs often run faster on machines with a larger word size, but they typically take up more memory. A 32-bit processor (or operating system) cannot use more than 4 gigabytes (defined below) of memory. Thus, a 64-bit computer is needed to take advantage of the larger amounts of memory that are now available. |
| Cache |
Human brains both perform computations and store information. A computer CPU performs computations, but for the most part, does not store information. The CPU cache is the exception. Most modern CPUs have a small, very fast section of memory built right onto the chip. By guessing what information the CPU is going to use next, it can pre-load it into the cache and avoid waiting around for the slower regular memory. Over time, caches have become more complicated and often have multiple levels. The first level is very small but incredibly fast. The second level is larger and slower. And so on. It would be preferable to have a large, first-level cache, but fast memory is expensive memory. Each level is larger, slower, and cheaper than the last. Cache size is not a heavily advertised CPU feature, but it makes a huge difference in performance. A processor with a larger cache can often outperform a processor that’s faster in terms of clock rate. |
| Cores |
Most laptops and desktops available today have multicore processors. These processors contain two, four, six, or even more cores. Each core is a processor capable of independently executing instructions, and they can all communicate with the same memory. In theory, having six cores could allow your computer to run six times as fast. In practice, this speedup is hard to achieve. Learning how to get more performance out of multicore systems is a major themes of this book. Chapter 13 and Chapter 14 as well as sections marked Concurrency in other chapters are specifically tailored for students interested in programming these multicore systems to work effectively. If you aren’t interested in concurrent programming, you can skip these chapters and sections and use this book as a traditional introductory Java programming textbook. On the other hand, if you are interested in the increasingly important area of concurrent programming, Section 1.4.1 near the end of this chapter is the first Concurrency section of the book and discusses multicore processors more deeply. |
Memory
Memory is where all the programs and data on a computer are stored. The memory in a computer is usually not a single piece of hardware. Instead, the storage requirements of a computer are met by many different technologies.
At the top of the pyramid of memory is primary storage, memory that the CPU can access and control directly. On desktop and laptop computers, primary storage usually takes the form of random access memory (RAM). It is called random access memory because it takes the same amount of time to access any part of RAM. Traditional RAM is volatile, meaning that its contents are lost when it’s unpowered. All programs and data must be loaded into RAM to be used by the CPU.
After primary storage comes secondary storage. The realm of secondary storage is dominated by hard drives that store data on spinning magnetic platters though flash technology is beginning to replace them. Optical drives (such as CD, DVD, and Blu-ray) and the now virtually obsolete floppy drives also fall into the category of secondary storage. Secondary storage is slower than primary storage, but it is non-volatile. Some forms of secondary storage such as CD-ROM and DVD-ROM are read only, but most are capable of reading and writing.
Before we can compare these kinds of storage effectively, we need to have a system for measuring how much they store. In modern digital computers, all data is stored as a sequence of 0s and 1s. In memory, the space that can hold either a single 0 or a single 1 is called a bit, which is short for “binary digit.”
A bit is a tiny amount of information. For organizational purposes, we call a sequence of eight bits a byte. The word size of a CPU is two or more bytes, but memory capacity is usually listed in bytes not words.

Both primary and secondary storage capacities have become so large that it is inconvenient to describe them in bytes. Computer scientists have borrowed prefixes from physical scientists to create suitable units.
Common units for measuring memory are bytes, kilobytes, megabytes, gigabytes, and terabytes. Each unit is 1,024 times the size of the previous unit. You may have noticed that 210 (1,024) is almost the same as 103 (1,000). Sometimes it’s not clear which value is meant. Disk drive manufacturers always use powers of 10 when they quote the size of their disks. Thus, a 1 TB hard disk might hold 1012 (1,000,000,000,000) bytes, not 240 (1,099,511,627,776) bytes. Standards organizations have advocated that the terms kibibyte (KiB), mebibyte (MiB), gibibyte (GiB), and tebibyte (TiB) be used to refer to the units based on powers of 2 while the traditional names be used to refer only to the units based on powers of 10, but the new terms have not yet become popular.
| Unit | Size | Bytes | Practical Measure |
|---|---|---|---|
byte |
8 bits |
20 = 100 |
a single character |
kilobyte (KB) |
1,024 bytes |
210 ≈ 103 |
a paragraph of text |
megabyte (MB) |
1,024 kilobytes |
220 ≈ 106 |
a minute of MP3 music |
gigabyte (GB) |
1,024 megabytes |
230 ≈ 109 |
an hour of standard definition streaming video |
terabyte (TB) |
1,024 gigabytes |
240 ≈ 1012 |
80% of human memory capacity, |
We called memory a pyramid earlier in this section. At the top there’s a small but very fast amount of memory. As we work down the pyramid, the storage capacity grows, but the speed slows down. Of course, the pyramid for every computer is different. Below is a table that shows many kinds of memory moving from the fastest and smallest to the slowest and largest. Effective speed is hard to measure (and is changing as technology progresses), but note that each layer in the pyramid tends to be 10-100 times slower than the previous layer.
| Memory | Typical Capacity | Use |
|---|---|---|
Cache |
kilobytes or megabytes |
Cache is fast, temporary storage for the CPU itself. Modern CPUs have two or three levels of cache that get progressively bigger and slower. |
RAM |
gigabytes |
The bulk of primary memory is RAM. RAM comes on sticks that can be swapped out to upgrade a computer. |
Flash drives |
gigabytes up to terabytes |
Flash drives provide some of the fastest secondary storage available to regular consumers. Flash drives come as USB keychain drives but also as drives that sit inside the computer (sometimes called solid state drives or SSDs). As the price of flash drives drops, they are expected to replace hard drives entirely. Some SSDs already have capacities in the terabyte range. |
Hard drives |
terabytes |
Hard drives are still the most common secondary storage for desktops, laptops, and servers. They are limited in speed partly because of their moving parts. |
Tape backup |
terabytes and beyond |
Some large companies still store huge quantities of information on magnetic tape. Tape performs well for long sequential accesses. |
Network storage |
terabytes and beyond |
Storage that is accessed through a network is limited by the speed of the network. Many companies use networked computers for backup and redundancy as well as distributed computation. Amazon, Google, Microsoft, and others rent their network storage systems at rates based on storage size and total data throughput. These services are part of what is called cloud computing. |
I/O devices
I/O devices have much more variety than CPUs or memory. Some I/O devices, such as USB ports, are permanently connected by a printed circuit board to the CPU. Other devices called peripherals are connected to a computer as needed. Their types and features are many and varied, and this book does not go deeply into how to interact with I/O devices.
Common input devices include mice, keyboards, touch pads, microphones, game pads, and drawing tablets. Common output devices include monitors, speakers, and printers. Some devices perform both input and output, such as network cards.
Remember that our view of computer hardware as CPU, memory, and I/O devices is only a model. A PCI Express socket can be considered an I/O device, but the graphics card that fits into the socket can be considered one as well. And the monitor that connects to the graphics card is yet another one. Although the graphics card is an I/O device, it has its own processor and memory, too. It’s pointless to get bogged down in details unless they are relevant to the problem you’re trying to solve. One of the most important skills in computer science is finding the right level of detail and abstraction to view a given problem.
1.2.2. Software
Without hardware computers would not exist, but software is equally important. Software consists of the programs and data that are executed and stored by the computer. The focus of this book is learning to write software.
Software includes the nearly infinite variety of computer programs. With the right tools (many of which are free), anyone can write a program that runs on a Windows, Mac, or Linux machine. Although it would be nearly impossible to list all the different kinds of software, a few categories are worth mentioning.
| Operating Systems |
The operating system (OS) is the software that manages the interaction between the hardware and the rest of the software. Programs called drivers are added to the OS for each hardware device. For example, when an application wants to print a document, it communicates with the printer via a printer driver that’s customized for the specific printer, the OS, and the computer hardware. The OS also schedules, runs, and manages memory for all other programs. The three most common OSes for desktop machines are Microsoft Windows, Apple macOS, and Linux. At the present time, all three run on similar hardware based on the Intel x86 and x64 architectures. Microsoft does not sell desktop computers, but many desktop and laptop computers come bundled with Windows. For individuals and businesses who assemble their own computer hardware, it’s also possible to purchase Windows separately. In contrast, almost all computers running macOS are sold by Apple, and macOS is usually bundled with the computer. Linux is open-source software, meaning that all the source code used to create it is freely available. In spite of Linux being free, many consumers prefer Windows or macOS because of ease of use, compatibility with specific software, and technical support. Many consumers are also unaware that hardware can be purchased separately from an OS or that Linux is a free alternative to the other two. Other computers have OSes as well. Many kinds of mobile telephones use the Google Android OS. The Apple iPad and iPhone use the competing Apple iOS. Phones, microwave ovens, automobiles, and countless other devices have computers in them that use some kind of embedded OS. Consider two applications running on a mobile phone with a single core CPU. One application is a web browser and the other is a music player. The user may start listening to music and then start the browser. In order to function, both applications need to access the CPU at the same time. Since the CPU only has a single core, it can execute only one instruction at a time. Rather than forcing the user to finish listening to the song before using the web browser, the OS switches the CPU between the two applications very quickly. This switching allows the user to continue browsing while the music plays in the background. The user perceives an illusion that both applications are using the CPU at the same time. |
| Compilers |
A compiler is a kind of program that’s particularly important to programmers. Computer programs are written in special languages, such as Java, that are human readable. A compiler takes this human-readable program and turns it into instructions (often machine code) that a computer can understand. To compile the programs in this book, you use the Java compiler
|
| Business Applications |
Many different kinds of programs fall under the umbrella of business or productivity software. Perhaps the best known is the Microsoft Office suite of tools, which includes the word-processing software Word, the spreadsheet software Excel, and the presentation software PowerPoint. Programs in this category are often the first to come to mind when people think of software, and this category has had tremendous historical impact. The popularity of Microsoft Office led to the widespread adoption of Microsoft Windows in the 1990s. A single application that’s so desirable that a consumer is willing to buy the hardware and the OS just to be able to run it is sometimes called a killer app. |
| Video Games |
Video games are software like other programs, but they deserve special attention because they represent an enormous, multi-billion dollar industry. They are usually challenging to program, and the video game development industry is highly competitive. The intense 3D graphics required by modern video games have pushed hardware manufacturers such as Nvidia, AMD, and Intel to develop high-performance graphics cards for desktop and laptop computers. At the same time, companies like Nintendo, Sony, and Microsoft have developed computers such as the Switch, PlayStation 4, and Xbox One that specialize in video games but are not designed for general computing tasks. |
| Web Browsers |
Web browsers are programs that can connect to the Internet and download and display web pages and other files. Early web browsers could only display relatively simple pages containing text and images. Because of the growing importance of communication over the Internet, web browsers have evolved to play sounds, display video, and allow for sophisticated real-time communication. Popular web browsers include Microsoft Edge, Mozilla Firefox, Apple Safari, and Google Chrome. Each has advantages and disadvantages in terms of compatibility, standards compliance, security, speed, and customer support. The Opera web browser is not well known on desktop computers, but it is used on many mobile telephones. |
1.3. Syntax: Data representation
After each Concepts section, this book usually has a Syntax section. Syntax is the set of rules for a language. These Syntax sections generally focus on concrete Java language features and technical specifics related to the concepts described in the chapter.
In this chapter, we’re still trying to describe computers at a general level. Consequently, the technical details we cover in this section will not be Java syntax. Although everything we say applies to Java, it also applies to many other programming languages.
1.3.1. Compilers and interpreters
This book is primarily about solving problems with computer programs. From now on, we only mention hardware when it has an impact on programming. The first step to writing a computer program is deciding what language to use.
Most humans communicate via natural languages such as Chinese, English, French, Russian, or Tamil. However, computers are poor at understanding natural languages. As a compromise, programmers write programs (instructions for a computer to follow) in a language more similar to a natural language than it is to the language understood by the CPU. These languages are called high-level languages, because they are closer to natural language (the highest level) than they are to machine language (the lowest level). We may also refer to machine language as machine code or native code.
Thousands of programming languages have been created over the years, but some of the most popular high-level languages of all time include Fortran, Cobol, Visual Basic, C, C++, Python, Java, JavaScript (which is almost entirely unrelated to Java) and C#.
As we mentioned in the previous section, a compiler is a program that translates one language into another. In many cases, a compiler translates a high-level language into a low-level language that the CPU can understand and execute. Because all the work is done ahead of time, this kind of compilation is known as static or ahead-of-time compilation. In other cases, the output of the compiler is an intermediate language that’s easier for the computer to understand than the high-level language but still takes some translation before the computer can follow the instructions.
An interpreter is a program with many similarities to a compiler. However, an interpreter takes code in one language as input and, on the fly, runs each instruction on the CPU as it translates it. Interpreters generally execute code more slowly than if it had been translated to machine language before execution.
Note that both compilers and interpreters are normal programs. They are usually written in high-level languages and compiled into machine language before execution. This raises a philosophical question: If you need a compiler to create a program, where did the first compiler come from?

Java is the popular high-level programming language we focus on in this book. The standard way to run a Java program has an extra step that many compiled languages do not. Most compilers for Java, though not all, translate a program written in Java to an intermediate language known as bytecode. This intermediate version of the high-level program is used as input for another program called the Java Virtual Machine (JVM). Most popular JVMs translate the bytecode into machine code that is executed directly by the CPU. This conversion from bytecode into machine code is done with a just-in-time (JIT) compiler. It’s called “just-in-time” because sections of bytecode are not compiled until the moment they’re needed. Since the output is going to be used for this specific execution of the program, the JIT can do optimizations to make the final machine code run particularly well in the current environment.
Why does Java use the intermediate step of bytecode? One of Java’s design goals is to be platform independent, meaning that it can be executed on any kind of computer. This is a difficult goal because every combination of OS and CPU will need different low-level instructions. Java attacks the problem by keeping its bytecode platform independent. You can compile a program into bytecode on a Windows machine and then run the bytecode on a JVM in a macOS environment. Part of the work is platform independent, and part is not. Each JVM must be tailored to the combination of OS and hardware that it runs on. Sun Microsystems, Inc., the original developer of the Java language and the JVM, marketed this feature of the language with the slogan “Write once, run anywhere.”
Sun Microsystems was bought by Oracle Corporation in 2009. Oracle continues to produce HotSpot, the standard JVM, but many other JVMs exist, including Apache Harmony and Dalvik, the Google Android JVM.
1.3.2. Numbers
All data inside of a computer is represented with numbers. Although humans use numbers in our daily lives, the representation and manipulation of numbers by computers function differently. In this subsection we introduce the notions of number systems, bases, conversion from one base to another, and arithmetic in arbitrary number systems.
A few number systems
A number system is a way to represent numbers. It’s easy to confuse the numeral that represents the number with the number itself. You might think of the number ten as “10”, a numeral made of two symbols, but the number itself is the concept of ten-ness. You could express that quantity by holding up all your fingers, with the symbol “X”, or by knocking ten times.
Representing ten with “10” is an example of a positional number system, namely base 10. In a positional number system, the position of the digits determines the magnitude they represent. For example, the numeral 3,432 contains the digit 3 twice. The first time, it represents three groups of one thousand. The second time, it represents three groups of ten. In contrast, the Roman numeral system is an example of a number system that is not positional.
The numeral 3,432 and possibly every other normally written number you’ve seen is expressed in base 10 or the decimal system. It’s called base 10 because, as you move from the rightmost digit leftward, the value of each position goes up by a factor of 10. Also, in base 10, ten is the smallest positive integer that requires two digits for representation. Each smaller number has its own digit: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Representing ten requires two existing digits to be combined. Every base has the property that the number it’s named after takes two digits to write, namely “1” and “0.” (An exception is base 1, which does not behave like the other bases and is not a normal positional number system.)
The number 723 can be written as 723 = 7 · 102 + 2 · 101 + 3 · 100.
Note that the rightmost digit is the ones place, which is equivalent to 100. Be sure to start with b0 and not b1 when considering the value of a number written in base b, no matter what b is. The second digit from the right is multiplied by 101, and so on. The product of a digit and the corresponding power of 10 tells us how much a digit contributes to the number. In the above expansion, digit 7 contributes 700 to the number 723. Digits 2 and 3 contribute, respectively, 20 and 3 to 723.
As we move to the right, the power of 10 goes down by one, and this pattern works even for negative powers of 10. If we expand the fractional value 0.324, we get 0.324 = 3 · 10-1 + 2 · 10-2 + 4 · 10-3.
We can combine the above two numbers to get 723.324 = 7 · 102 + 2 · 101 + 3 · 100 + 3 · 10-1 + 2 · 10-2 + 4 · 10-3.
We can extend these ideas to any base, checking our logic against the familiar base 10. Suppose that a numeral consists of n symbols sn-1, sn-2, …, s1, s0. Furthermore, suppose that this numeral belongs to the base b number system. We can expand the value of this numeral as:
sn-1 sn-2 … s1 s0 = sn-1 · bn-1 + sn-2 · bn-2 + … + s1 · b1 + s0 · b0
The leftmost symbol in the numeral is the highest order digit and the rightmost symbol is the lowest order digit. For example, in the decimal numeral 492, 4 is the highest order digit and 2 the lowest order digit.
Fractions can be expanded in a similar manner. For example, a fraction with n symbols s1, s2, …, sn-1, sn in a number system with base b can be expanded to:
0.s1 s2 … sn-2 sn-1 = s1 · b-1 + s2 · b-2 + … + sn-1 · b-n+1 + sn · b-n
As computer scientists, we have a special interest in base 2 because that’s the base used to express numbers inside of computers. Base 2 is also called binary. The only symbols allowed to represent numbers in binary are “0” and “1”, the binary digits or bits.
In the binary numeral 10011, the leftmost 1 is the highest order bit and the rightmost 0 is the lowest order bit. By the rules of positional number systems, the highest order bit represents 1 · 24 = 16.
Examples of numbers written in binary are 1002, 1112, 101012, and 110000012. Recall that the base of the binary number system is 2. Thus, we can write a number in binary as the sum of products of powers of 2. For example, the numeral 100112 can be expanded to:
100112 = 1 · 24 + 0 · 23 + 0 · 22 + 1 · 21 + 1 · 20 = 16 + 0 + 0 + 2 + 1 = 19
By expanding the number, we’ve also shown how to convert a binary numeral into a decimal numeral. Remember that both 100112 and 19 represent the same value, namely nineteen. The conversion between bases changes only the way the number is written. As before, the rightmost bit is multiplied by 20 to determine its contribution to the binary number. The bit to its left is multiplied by 21 to determine its contribution, and so on. In this case, the leftmost 1 contributes 1 · 24 = 16 to the value.
Another useful number system is base 16, also known as hexadecimal. Hexadecimal is surprising because it requires more than the familiar 10 digits. Numerals in this system are written with 16 hexadecimal digits that include the ten digits 0 through 9 and the six letters A, B, C, D, E, and F. The six letters, starting from A, correspond to the values 10, 11, 12, 13, 14, and 15.
Hexadecimal is used as a compact representation of binary. Although binary numbers can get very long, four binary digits can be represented with only a single hexadecimal digit.
39A16, 3216, and AFBC1216 are examples of numbers written in hexadecimal. A hexadecimal numeral can be expressed as the sum of products of powers of 16. For example, the hexadecimal numeral A0BF16 can be expanded to:
A · 163 + 0 · 162 + B · 161 + F · 160
To convert a hexadecimal numeral to decimal, we must substitute the values 10 through 15 for the digits A through F. Now we can rewrite the sum of products from above as:
10 · 163 + 0 · 162 + 11 · 161 + 15 · 160 = 40,960 + 0 + 176 + 15 = 41,151
Thus, we get A0BF16 = 41,151.
The base 8 number system is also called octal. Like hexadecimal, octal is used as a shorthand for binary. A numeral in octal uses the octal digits 0, 1, 2, 3, 4, 5, 6, and 7. Otherwise the same rules apply. For example, the octal numeral 377 can be expanded to:
3778 = 3 · 82 + 7 · 81 + 7 · 80 = 255
You may have noticed that it is not always clear which base a numeral is written in. The digit sequence 337 is a legal numeral in octal, decimal, and hexadecimal, but it represents different numbers in each system. Mathematicians use a subscript to denote the base in which a numeral is written.
Thus, 3378 = 25510, 37710 = 37710,
and 37716 = 88710. Base numbers are always written
in base 10. A number without a subscript is assumed to be in base 10. In
Java, there’s no way to mark subscripts, so prefixes are used. A
prefix of 0 is used for octal, no prefix is used for decimal, and a prefix
of 0x is used for hexadecimal. A numeral cannot be marked as binary in
Java. The corresponding numerals in Java code would thus be written 0377, 377,
and 0x377. Be careful not to pad numbers with zeroes in Java since they might be interpreted as base 8! Remember that
the value 056 is not the same as the value 56 in Java.
The following table lists a few characteristics of the four number systems we have discussed with representations of the numbers 7 and 29.
| Number System | Base | Digits | Math Numerals |
Java Numerals |
|---|---|---|---|---|
Binary |
2 |
0, 1 |
1112, 111012 |
N/A |
Octal |
8 |
0, 1, 2, 3, 4, 5, 6, 7 |
78, 358 |
|
Decimal |
10 |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
7, 29 |
|
Hexadecimal |
16 |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
716, 1D16 |
|
Conversion across number systems
It’s useful to know how to convert a number represented in one base to the equivalent representation in another base. Our examples have shown how to convert a numeral in any base to decimal by expanding the numeral in the sum-of-product form and then adding the different terms together. But how do you convert a decimal numeral to another base?
Decimal to binary conversion
There are at least two different ways to convert a decimal numeral to binary. One way is to write the decimal number as a sum of powers of two as in the following conversion of the number 23.
23 = 16 + 0 + 4 + 2 + 1 = 1 · 24 + 0 · 23 + 1 · 22 + 1 · 21 + 1 · 20 = 101112
First, find the largest power of two that’s less than or equal to the number. In this case, 16 fits the bill because 32 is too large. Subtract that value from the number, leaving 7 in this case. Then repeat the process. The last step is to collect the coefficients of the powers of two into a sequence to get the binary equivalent. We used 16, 4, 2, and 1 but skipped 8. If we write a 1 for every place we used and a 0 for every place we skipped, we get 23 = 101112. While this is a straightforward procedure for decimal to binary conversion, it can be cumbersome for larger numbers.
An alternate way to convert a decimal numeral to an equivalent binary numeral is to divide the given number by 2 until the quotient is 0 (keeping only the integer part of the quotient). At each step, record the remainder found when dividing by 2. Collect these remainders (which will always be either 0 or 1) to form the binary equivalent. The least significant bit is the remainder obtained after the first division, and the most significant bit is the remainder obtained after the last division. In other words, this approach finds the digits of the binary number in backward order.
Let’s use this method to convert 23 to its binary equivalent. The following table shows the steps need for the conversion. The leftmost column lists the step number. The second column contains the number to be divided by 2 at each step. The third column contains the quotient for each step, and the last column contains the current remainder.
| Step | Number | Quotient | Remainder |
|---|---|---|---|
1 |
23 |
11 |
1 |
2 |
11 |
5 |
1 |
3 |
5 |
2 |
1 |
4 |
2 |
1 |
0 |
5 |
1 |
0 |
1 |
We begin by dividing 23 by 2, yielding 11 as the quotient and 1 as the remainder. The quotient 11 is then divided by 2, yielding 5 as the quotient and 1 as the remainder. This process continues until we get a quotient of 0 and a remainder of 1 in Step 5. We now write the remainders from the most recent to the least recent and get the same result as before, 23 = 101112.
Other conversions
A decimal number can be converted to its hexadecimal equivalent using either of the two procedures described above. Instead of writing a decimal number as a sum of powers of 2, one writes it as a sum of powers of 16. Similarly, when using the division method, instead of dividing by 2, one divides by 16. Octal conversion is similar.
We use hexadecimal because it’s straightforward to convert from it to binary or back. The following table lists binary equivalents for the 16 hexadecimal digits.
| Hexadecimal Digit |
Binary Equivalent |
Hexadecimal Digit |
Binary Equivalent |
|
|---|---|---|---|---|
0 |
0000 |
8 |
1000 |
|
1 |
0001 |
9 |
1001 |
|
2 |
0010 |
A |
1010 |
|
3 |
0011 |
B |
1011 |
|
4 |
0100 |
C |
1100 |
|
5 |
0101 |
D |
1101 |
|
6 |
0110 |
E |
1110 |
|
7 |
0111 |
F |
1111 |
With the help of the table above, let’s convert 3FA16 to binary. By simple substitution, 3FA16 = 0011 1111 10102. Note that we’ve grouped the binary digits into clusters of 4 bits each. Of course, the leftmost zeroes in the binary equivalent are useless as they do not contribute to the value of the number.
Integer representation in a computer
In mathematics, binary numerals can represent arbitrarily big numbers. Inside of a computer, the size of a number is constrained by the number of bits used to represent it. For general purpose computation, 32- and 64-bit integers are commonly used. The largest integer that Java represents with 32 bits is 2,147,483,647, which is good enough for most tasks. For larger numbers, Java can represent up to 9,223,372,036,854,775,807 with 64 bits. Java also provides representations for integers using 8 and 16 bits.
These representations are easy to determine for positive numbers: Find
the binary equivalent of the number and then pad the left side with
zeroes to fill the remaining space. For example,
19 = 100112. If stored using 8 bits, 19 would be
represented as 0001 0011. If stored using 16 bits, 19 would be
represented as 0000 0000 0001 0011. (We separate groups of 4 bits for
easier reading.)
Binary arithmetic
Recall that computers deal with numbers in their binary representation,
meaning that all arithmetic is done on binary numbers. Sometimes it’s
useful to understand how this process works and compare it to decimal arithmetic.
The table below lists rules for
binary addition.
+ |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
10 |
As indicated above, the addition of two 1s leads to a 0 with a carry of 1 into the next position to the left. Addition for numbers composed of more than one bit use the same rules as any addition, carrying values that are too large into the next position. In decimal addition, values over 9 must to be carried. In binary addition, values over 1 must be carried. The next example shows a sample binary addition. To simplify its presentation, we assume that the integers are represented with only 8 bits.
Let’s add the numbers 60 and 6 in binary. Using the conversion
techniques described above, we can find that 60 = 1111002
and 6 = 1102. Inside the computer, these numbers would
already be in binary and padded to fill 8 bits.
| Binary | Decimal | |
|---|---|---|
|
|
|
+ |
|
|
|
|
The result is no surprise, but note that the addition can proceed in binary without conversion to decimal at any point.
Subtraction in binary is also similar to subtraction in decimal. The rules are given in the following table.
- |
0 |
1 |
0 |
0 |
1 |
1 |
(1)1 |
0 |
When subtracting a 1 from a 0, a 1 is borrowed from the next left position. The next example illustrates binary subtraction.
Again, we’ll use 60 and 6 and their binary equivalents given above.
| Binary | Decimal | |
|---|---|---|
|
|
|
- |
|
|
|
|
Negative integers in a computer
Negative integers are also represented in computer memory as binary numbers, using a system called two’s complement. When looking at the binary representation of a signed integer in a computer, the leftmost (most significant) bit will be 1 if the number’s negative and 0 if it’s positive. Unfortunately, there’s more to finding the representation of a negative number than flipping this bit.
Suppose that we need to find the binary equivalent of the decimal number
-12 using 8 bits in two’s complement form. The first step
is to convert 12 to its 8-bit binary equivalent. Doing so we get 12 =
0000 1100. Note that the leftmost bit of the representation is a 0,
indicating that the number is positive. Next, we take the two’s
complement of the 8-bit representation in two steps. In the first step,
we flip every bit, i.e., change every 0 to 1 and every 1 to 0. This
gives us the one’s complement of the number, 1111 0011. In the
second step, we add 1 to the one’s complement to get the two’s
complement. The result is 1111 0011 + 1 = 1111 0100.
Thus, the 8-bit, two’s complement binary equivalent of -12 is
1111 0100. Note that the leftmost bit is a 1, indicating that this is
a negative number.
Let’s convert -29 to its binary equivalent assuming that the number will
be stored in 8-bit, two’s complement form. First we convert positive 29 to its 8-bit binary equivalent, 29 = 0001 1101.
Next we obtain the one’s complement of the binary representation by
flipping 0s to 1s and 1s to 0s. This gives us 1110 0010. Finally, we
add 1 to the one’s complement representation to get 1110 0010 + 1 =
1110 0011, which is the desired binary equivalent of -29.
Let’s convert the 8-bit, two’s complement value 1000 1100 to
decimal. We note that the leftmost bit of this number is 1, making it a
negative number. Therefore, we reverse the process of making a two’s
complement. First, we subtract 1 from the representation, yielding
1000 1100 - 1 = 1000 1011. Next, we flip all the bits in this
one’s complement form, yielding 0111 0100.
We convert this binary representation to its decimal equivalent,
yielding 116. Thus, the decimal equivalent of 1000 1100 is -116.
Why do computers use two’s complement? First of all, they need a system that can represent both positive and negative numbers. They could have used the leftmost bit as a sign bit and represented the rest of the number as a positive binary number. Doing so would require a check on the bit and some conversion for negative numbers every time a computer wanted to perform an addition or subtraction.
Because of the way it’s designed, positive and negative integers stored in two’s complement can be added or subtracted without any special conversions. The leftmost bit is added or subtracted just like any other bit, and values that carry past the leftmost bit are ignored. Two’s complement has an advantage over one’s complement in that there is only one representation for zero. The next example shows two’s complement in action.
We’ll add -126 and 126. After performing the needed conversions, their
8-bit, two’s complement representations are 1000 0010 and 0111 1110.
| Binary | Decimal | |
|---|---|---|
|
|
|
+ |
|
|
|
|
As expected, the sum is 0.
Now, let’s add the two negative integers -126 and -2, whose 8-bit, two’s
complement representations are 1000 0010 and 1111 1110.
| Binary | Decimal | |
|---|---|---|
|
|
|
+ |
|
|
|
|
The result is -128, which is the smallest negative integer that can be represented in 8-bit two’s complement.
Overflow and underflow
When performing arithmetic on numbers, an overflow is said to occur when the result of the operation is larger than the largest value that can be stored in that representation. An underflow is said to occur when the result of the operation is smaller than the smallest possible value.
Both overflows and underflows lead to wrapped-around values. For example, adding two positive numbers together can result in a negative number or adding two negative numbers together can result in a positive number.
Let’s add the numbers 124 and 6. Their 8-bit, two’s complement
representations are 0111 1100 and 0000 0110.
Binary |
Decimal |
|
|
|
|
+ |
|
|
|
|
This surprising result happens because the largest 8-bit two’s complement integer is 127. Adding 124 and 6 yields 130, a value larger than this maximum, resulting in overflow with a negative answer.
The smallest (most negative) number that can be represented in 8-bit two’s complement is -128. A result smaller than this will result in underflow. For example, -115 - 31 = 110. Try out the conversions needed to test this result.
Bitwise operators
Although we most commonly manipulate numbers using traditional mathematical operations such as addition, subtraction, multiplication, and division, there are also operations that work directly on the binary representations of the numbers. Some of these operators have clear relationships to mathematical operations, and some don’t.
| Operator | Name | Description |
|---|---|---|
|
Bitwise AND |
Combines two binary representations into a new representation which has a 1 in every position where both the original representations have a 1 |
|
Bitwise OR |
Combines two binary representations into a new representation which has a 1 in every position where either of the original representations has a 1 |
|
Bitwise XOR |
Combines two binary representations into a new representation which has a 1 in every position that the original representations have different values |
|
Bitwise complement |
Takes a representation and creates a new representation in which every bit is flipped from 0 to 1 and 1 to 0 |
|
Signed left shift |
Moves all the bits the specified number of positions to the left, shifting 0s into the rightmost bits |
|
Signed right shift |
Moves all the bits the specified number of positions to the right, padding the left with copies of the sign bit |
|
Unsigned right shift |
Moves all the bits the specified number of positions to the right, padding with 0s |
Bitwise AND, bitwise OR, and bitwise XOR take two integer representations and combine them to make a new representation. In bitwise AND, each bit in the result will be a 1 if both of the original integer representations in that position are 1 and 0 otherwise. In bitwise OR, each bit in the result will be a 1 if either of the original integer representations in that position are 1 and 0 otherwise. In bitwise XOR, each bit in the result will be a 1 if the two bits of the original integer representations in that position are different and 0 otherwise.
Bitwise complement is a unary operator like the negation operator (-).
Instead of merely changing the sign of a value (which it will also do),
its result changes every 1 in the original representation to 0 and
every 0 to 1.
The signed left shift, signed right shift, and unsigned right shift operators all create a new binary representation by shifting the bits in the original representation a certain number of places to the left or the right. The signed left shift moves the bits to the left, padding with 0s. If you do a signed left shift by n positions, it’s equivalent to multiplying the number by 2n (until overflow occurs). The signed right shift moves the bits to the right, padding with whatever the sign bit is. If you do a signed right shift by n positions, it’s equivalent to dividing the number by 2n (with integer division). The unsigned right shift moves the bits to the right, including the sign bit, filling the left side with 0s. An unsigned right shift will always make a value positive but is otherwise similar to a signed right shift. A few examples follow.
Here are a few examples of the result of bitwise operations. We’ll assume that the values are represented using 32-bit two’s complement, instead of using 8-bit values as before. In Java, bitwise operators automatically convert smaller values to 32-bit representations before proceeding.
Let’s consider the result of 21 & 27.
| Binary | Decimal | |
|---|---|---|
|
21 |
|
|
|
27 |
|
17 |
Note how this result is different from 21 | 27.
| Binary | Decimal | |
|---|---|---|
|
21 |
|
|
|
27 |
|
31 |
And also from 21 ^ 27.
| Binary | Decimal | |
|---|---|---|
|
21 |
|
|
|
27 |
|
14 |
Ignoring overflow, signed left shifting is equivalent to repeated
multiplications by 2. Consider 11 << 3. The representation
0000 0000 0000 0000 0000 0000 0000 1011 is shifted to the left to make
0000 0000 0000 0000 0000 0000 0101 1000 = 88 = 11 · 23.
Signed right shifting is equivalent to repeated integer divisions by 2.
Consider -104 >> 2. The representation
1111 1111 1111 1111 1111 1111 1001 1000 is shifted to the right to
make 1111 1111 1111 1111 1111 1111 1110 0110 = -26 = -104 ÷ 22.
Unsigned right shifting is the same as signed right shifting except when
it is done on negative numbers. Since their sign bit is replaced by 0,
an unsigned right shift produces a (generally large) positive number.
Consider -104 >>> 2. The representation
1111 1111 1111 1111 1111 1111 1001 1000 is shifted to the right to
make 0011 1111 1111 1111 1111 1111 1110 0110 = 1,073,741,798.
Because of the way two’s complement is designed, bitwise complement is
equivalent to negating the sign of the number and then subtracting
1. Consider ~(-104). The
representation 1111 1111 1111 1111 1111 1111 1001 1000 is complemented
to 0000 0000 0000 0000 0000 0000 0110 0111 = 103.
Rational numbers
We’ve seen how to represent positive and negative integers in computer memory, but this section shows how rational numbers, such as 12.33, -149.89, and 3.14159, can be converted into binary and represented.
Scientific notation
Scientific notation is closely related to the way a computer represents a rational number in memory. Scientific notation is a tool for representing very large or very small numbers without writing a lot of zeroes. A decimal number in scientific notation is written a × 10b where a is called the mantissa and b is called the exponent.
For example, the number 3.14159 can be written in scientific notation as 0.314159 × 101. In this case, 0.314159 is the mantissa, and 1 is the exponent. Here a few more examples of writing numbers in scientific notation.
3.14159 |
= |
3.14159 × 100 |
3.14159 |
= |
314159 × 10-5 |
-141.324 |
= |
-0.141324 × 103 |
30,000 |
= |
.3 × 105 |
There are many ways of writing any given number in scientific notation. A more standardized way of writing real numbers is normalized scientific notation. In this notation, the mantissa is always written as a number whose absolute value is less than 10 but greater than or equal to 1. Following are a few examples of decimal numbers in normalized scientific notation.
3.14159 |
= |
3.14159 × 100 |
-141.324 |
= |
-1.41324 × 102 |
30,000 |
= |
3.0 × 104 |
A shorthand for scientific notation is E notation, which is written with the mantissa followed by the letter ‘E’ followed by the exponent. For example, 39.2 in E notation can be written 3.92E1 or 0.392E2. The letter ‘E’ should be read “multiplied by 10 to the power.” It’s legal to use E notation to represent numbers in scientific notation in Java.
Fractions
A rational number can be broken into an integer part and a fractional part. In the number 3.14, 3 is the integer part, and .14 is the fractional part. We’ve already seen how to convert the integer part to binary. Now, we’ll see how to convert the fractional part into binary. We can then combine the binary equivalents of the integer and fractional parts to find the binary equivalent of a decimal real number.
A decimal fraction f is converted to its binary equivalent by successively multiplying it by 2. At the end of each multiplication step, either a 0 or a 1 is obtained as an integer part and is recorded separately. The remaining fraction is again multiplied by 2 and the resulting integer part recorded. This process continues until the fraction reduces to zero or enough binary digits for the desired precision have been found. The binary equivalent of f then consists of the bits in the order they have been recorded, as shown in the next example.
Let’s convert 0.8125 to binary. The table below shows the steps to do so.
| Step | f | 2f | Integer part | Remainder |
|---|---|---|---|---|
1 |
0.8125 |
1.625 |
1 |
0.625 |
2 |
0.625 |
1.25 |
1 |
0.25 |
3 |
0.25 |
0.5 |
0 |
0.5 |
4 |
0.5 |
1.0 |
1 |
0 |
We then collect all the integer parts and get 0.11012 as the binary equivalent of 0.8125. We can convert this binary fraction back into decimal to verify that it’s correct.
0.11012 = 1 · 2-1 + 1 · 2-2 + 0 · 2-3 + 1 · 2-4 = 0.5 + 0.25 + 0 + 0.0625 = 0.8125
In some cases the process described above will never have a remainder of 0. Then, we can only find an approximate representation of the given fraction as demonstrated in the next example.
Let’s convert 0.3 to binary assuming that we have only five bits in
which to represent the fraction. The following table shows the five
steps in the conversion process.
| Step | f | 2f | Integer part | Remainder |
|---|---|---|---|---|
1 |
0.3 |
0.6 |
0 |
0.6 |
2 |
0.6 |
1.2 |
1 |
0.2 |
3 |
0.2 |
0.4 |
0 |
0.4 |
4 |
0.4 |
0.8 |
0 |
0.8 |
5 |
0.8 |
1.6 |
1 |
0.6 |
Collecting the integer parts we get 0.010012 as the binary representation of 0.3. Let’s convert this back to decimal to see how accurate it is.
0.010012 = 0 · 2-1 + 1 · 2-2 + 0 · 2-3 + 0 · 2-4 + 1 · 2-5 = 0 + 0.25 + 0 + 0 + 0.03125 = 0.28125
Five bits are not enough to represent 0.3 fully. Indeed, perfect accuracy would require an infinite number of bits! In this case, we have an error of 0.3 - 0.28125 = 0.01875. Most computers use many more bits to represent fractions and obtain much better accuracy in their representation.
Now that we understand how integers as well as fractions can be converted from one number base to another, we can convert any rational number from one base to another. The next example demonstrates one such conversion.
Let’s convert 14.3 to binary assuming that we’ll only use six bits to represent the fractional part. First we convert 14 to binary using the technique described earlier. This gives us 14 = 11102. Taking the method outlined in Example 1.14 one step further, our six bit representation of 0.3 is 0.0100112. Combining the two representations gives 14.3 = 1110.0100112.
Floating-point representation
Floating-point representation is a system used to represent rational numbers in computer memory. In this notation a number is represented as a × be, where a gives the significant digits (mantissa) of the number and e is the exponent. The system is very similar to scientific notation, but computers usually use base b = 2 instead of 10.
For example, we could write the binary number 1010.12 in floating-point representation as 10.1012 × 22 or as 101.012 × 21. In any case, this number is equivalent to 10.5 in decimal.
In standardized floating-point representation, a is written so that only the most significant non-zero digit is to the left of the decimal point. Most computers use the IEEE 754 floating-point representation to represent rational numbers. In this notation, the memory to store the number is divided into three segments: one bit used to mark the sign of the number, m bits to represent the mantissa (also known as the significand), and e bits to represent the exponent.
In IEEE floating-point representation, numbers are commonly represented using 32 bits (known as single precision) or using 64 bits (known as double precision). In single precision, m = 23 and e = 8. In double precision, m = 52 and e = 11. To represent positive and negative exponents, the exponent has a bias added to it so that the result is never negative. This bias is 127 for single precision and 1,023 for double precision. The packing of the sign bit, the exponent, and the mantissa is shown in Figure 1.4 (a) and (b).
The following is a step-by-step demonstration of how to construct the single precision binary representation in IEEE format of the number 10.5.
-
Convert 10.5 to its binary equivalent using methods described earlier, yielding 10.510 = 1010.12. Unlike the case of integers, the sign of the number is taken care of separately for floating-point. Thus, we would use 1010.12 for -10.5 as well.
-
Write this binary number in standardized floating-point representation, yielding 1.01012 × 23.
-
Remove the leading bit (always a 1 for non-zero numbers), leaving
0101. -
Pad the fraction with zeroes on the right to fill the 23-bit mantissa, yielding
0101 0000 0000 0000 0000 000. Note that the decimal point is ignored in this step. -
Add 127 to the exponent. This gives us an exponent of 3 + 127 = 130.
-
Convert the exponent to its 8-bit unsigned binary equivalent. Doing so gives us 13010 = 100000102.
-
Set the sign bit to 0 if the number is positive and to 1 otherwise. Since 10.5 is positive, we set the sign bit to 0.
We now have the three components of 10.5 in binary. The memory representation of 10.5 is shown in Figure 1.4 (c). Note in the figure how the sign bit, the exponent, and the mantissa are packed into 32 bits.

Largest and smallest numbers
Fixing the number of bits used for representing a real number limits the
numbers that can be represented in computer memory using the floating-point
notation. The largest rational number that can be represented in
single precision has an exponent of 127 (254 after bias) with a mantissa
consisting of all 1s:
0 1111 1110 1111 1111 1111 1111 1111 111
This number is approximately 3.402 × 1038. To
represent the smallest (closest to zero) non-zero number, we need to
examine one more complication in the IEEE format. An exponent of 0
implies that the number is unnormalized. In this case, we no longer
assume that there is a 1 bit to the left of the mantissa. Thus, the
smallest non-zero single precision number has its exponent set to 0 and
its mantissa set to all zeros with a 1 in its
23rd bit:
0 0000 0000 0000 0000 0000 0000 0000 001
Unnormalized single precision values are considered to have an exponent
of -126. Thus, the value of this number is
2-23 × 2-126 =
2-149 ≈ 1.4 × 10-45. Now that we know the rules for
storing both integers and floating-point numbers, we can list the
largest and smallest values possible in 32- and 64-bit representations
in Java in the following table. Note that largest means the
largest positive number for both integers and floating-point values, but
smallest means the most negative number for integers and the smallest
positive non-zero value for floating-point values.
| Format | Largest number | Smallest number |
|---|---|---|
32-bit integer |
2,147,483,647 |
-2,147,483,648 |
64-bit integer |
9,223,372,036,854,775,807 |
-9,223,372,036,854,775,808 |
32-bit floating-point |
3.4028235 × 1038 |
1.4 × 10-45 |
64-bit floating-point |
1.7976931348623157 × 10308 |
4.9-324 |
Using the same number of bits, floating-point representation can store much larger numbers than integer representation. However, floating-point numbers are not always exact, resulting in approximate results when performing arithmetic. Always use integer formats when fractional parts aren’t needed.
Special numbers
Several binary representations in the floating-point representation correspond to special numbers. These numbers are reserved and do not have the values that would be expected from normal multiplication of the mantissa by the power of 2 given by the exponent.
- 0.0 and -0.0
-
When the exponent and the mantissa are both 0, the number is interpreted as a 0.0 or -0.0 depending on the sign bit. For example, in a Java program, dividing 0.0 by -1.0 results in -0.0. Similarly, -0.0 divided by -1.0 is 0.0. Positive and negative zeroes only exist for floating-point values. -0 is the same as 0 for integers. Dividing the integer 0 by -1 in Java results in 0 and not in -0.
- Positive and negative infinity
-
An overflow or an underflow might occur while performing arithmetic on floating-point values. In the case of an overflow, the resulting number is a special value that Java recognizes as infinity. In the case of an underflow, it is a special negative infinity value. For example, dividing 1.0 by 0.0 in Java results in infinity and dividing -1.0 by 0.0 results in negative infinity. These values have well defined behavior. For example, adding 1.0 to infinity yields infinity.
Note that floating-point values and integers do not behave in the same way. Dividing the integer 1 by the integer 0 creates an error that can crash a Java program. - Not-a-number (
NaN) -
Some mathematical operations may result in an undefined number. For example, the square root of a negative number is an imaginary number. Java has a value set aside for results that are not rational numbers. When we discuss how to find the square root of a value in Java, this not-a-number value will be the answer for the square root of a negative number.
Errors in floating-point arithmetic
As we have seen, many rational numbers can only be approximately
represented in computer memory. Thus, arithmetic done on the approximate
values yields approximate answers. For example, 1.3 cannot be
represented exactly using a 64-bit value. In this case, the product
1.3 * 3.0 will be 3.9000000000000004 instead of 3.9. This error will propagate as
additional operations are performed on previous results. The next
example illustrates this propagation of errors when a sequence of
floating-point operations are performed.
Suppose that the price of several products is added to determine
the total price of a purchase at a cash register that uses floating-point arithmetic with a 32-bit variable (the equivalent of a float in Java).
For simplicity, let’s assume that all items have a
price of $1.99. We don’t know how many items will be purchased ahead of
time and simply add the price of each item until all items have been
scanned at the register. The table below shows the value of the total
cost for different quantities of items.
| Items | Correct Cost | Calculated Cost | Absolute Error | Relative Error |
|---|---|---|---|---|
100 |
199.0 |
1.9900015E02 |
1.5258789E-04 |
7.6677333E-07 |
500 |
995.0 |
9.9499670E02 |
3.2958984E-03 |
3.3124606E-06 |
1000 |
1990.0 |
1.9899918E03 |
8.1787109E-03 |
4.1099051E-06 |
10000 |
19900.0 |
1.9901842E04 |
1.8417969E00 |
9.2552604E-05 |
The first column in the table above is the number of items. The second column is the correct cost of all items purchased. The third column is the cost calculated by adding each item using single precision floating-point addition. The fourth and fifth columns give the absolute and relative errors, respectively, of the calculated value. Note how the error increases as the number of additions goes up. In the last row, the absolute error is almost two dollars.
While the above example may seem unrealistic, it does expose the inherent dangers of floating-point calculations. Although the error is less when using double precision representations, it still exists.
1.4. Solution: Buying a computer
We pose a motivating problem in the Problem section near the beginning of most chapters. Whenever there is a Problem section, there is a Solution section near the end in which we give a solution to the earlier problem.
After all the discussion of the hardware, software, and data representation inside of a computer, you might feel more confused about which computer to buy than before. As a programmer, it’s important to understand how data is represented, but this information plays virtually no role in deciding which computer to buy. Unlike most problems in this book, there’s no concrete answer we can give here. Because the development of technology progresses so rapidly, any advice about computer hardware or software has a short shelf-life.
Software is a huge consideration, beginning with the OS. Because the choice of OS usually affects choice of hardware, we’ll start there. The three major choices for a desktop or laptop OS are Microsoft Windows, Apple macOS, and Linux.
Windows is heavily marketed for business use. Windows suffered from many stability and security issues, but Microsoft has worked hard to address these. Apple macOS and the computers it’s installed on are marketed to an artistic and counter-culture population. Linux is popular among tech savvy users. Putting marketing biases aside, the three operating systems have become more similar over time, and most people could be productive using any of the three. The following table lists some pros and cons for each OS.
| OS | Pros | Cons |
|---|---|---|
Microsoft Windows |
|
|
Apple macOS |
|
|
Linux |
|
|
Once you’ve decided on an OS, you can pick hardware and other software that’s compatible with it. For macOS, almost all your hardware choices will be computers sold by Apple. For Windows and Linux, you can either have a computer built for you or build your own. Although computer hardware changes quickly, let’s examine some general guidelines.
- CPU
-
Remember that the speed of a CPU is measured in GHz (billions of clock cycles per second). Higher GHz is generally better, but it’s hard to compare performance across different designs of CPU. There’s also a diminishing returns effect: The very fastest, very newest CPUs are often considerably more expensive even if they only provide slightly better performance. It’s usually more cost effective to select a CPU in the middle of the performance spectrum.
Cache size also has a huge effect on performance. The larger the cache, the less often the CPU has to read data from slower memory. Since most new CPUs available today are 64-bit, the question of word size is no longer significant.
Although some specialists may prefer one or the other, both Intel and AMD make powerful, competitive consumer CPUs.
- Memory
-
Memory includes RAM, hard drives, optical drives, and any other storage. RAM is usually easy to upgrade for desktop machines and less easy (though often possible) for laptops. The price of RAM per gigabyte goes down over time. It may be reasonable to start with a modest amount of RAM and then upgrade after a year or two when it becomes cheaper to do so. It takes a little bit of research to get exactly the right kind of RAM for your CPU and motherboard. The amount of RAM is dependent on what you want to do with your system. The minimum amount of RAM to run Microsoft Windows 10 is 1 GB for 32-bit versions and 2 GB for 64-bit versions. The minimum amount of RAM to run Apple macOS Mojave is 2 GB. One rule of thumb is to have at least twice the minimum required RAM.
Hard drive space is dependent on how you expect to use your computer. 1 TB and 2 TB drives are not very expensive, and either represents a huge amount of storage. Only if you plan to have enormous libraries of video or uncompressed audio data will you likely need more. Corporate level databases and web servers and some other business systems can also require vast amounts of space. Hard drive speed is greatly affected by the hard drive’s cache size. As always, a bigger cache means better performance. Using a solid state drive (SSD) instead of a traditional hard drive has much better performance but higher cost per megabyte. If you can afford an SSD, this single upgrade is likely to feel like the greatest increase in overall computer speed.
Installing optical drives and other storage devices depends on individual needs. With the rise of streaming services and cloud backup, optical drives have become less popular.
- I/O Devices
-
The subject of I/O devices is personal. It’s difficult to say what anyone should buy without considering his or her specific needs. A monitor is the essential visual output device while a keyboard and mouse are the essential input devices. Speakers are important as well. Most laptops have all of these elements integrated in some form or another. Laptops often have inexpensive web cameras installed as well.
Someone interested in video games might want to invest in a powerful graphics card. Newer cards with more video RAM are generally better than older cards with less, but which card is best at a given price point is the subject of continual discussion at sites like AnandTech and Tom’s Hardware.
Printers are still useful output devices. Graphics tablets can make it easier to create digital art on a computer. The number of potentially worthwhile I/O devices is limitless.
This section is a jumping off point for purchasing a computer. As you learn more about computer hardware and software, it will become easier to know what combination of the two will serve your needs. Of course, there’s always more to know, and technology changes quickly.
1.4.1. Concurrency: Multicore processors
In the last decade, the word “core” has been splattered all over CPU packaging. Intel in particular has marketed the idea heavily with its older Core and Core 2 models and its modern Core i3, Core i5, Core i7, and Core i9 chips. What are all these cores?
Looking back into the past, most consumer processors had a single core, or brain. They could only execute one instruction at a time. Even this definition is hazy, because pipelining kept more than one instruction in the process of being executed, but overall execution proceeded sequentially.
The advent of multicore processors has changed this design significantly. Each processor has several independent cores, each of which can execute different instructions at the same time. Before the arrival of multicore processors, a few desktop computers and many supercomputers had multiple separate processors that could achieve a similar effect. However, since multicore processors have more than one effective processor on the same silicon die, the communication time between processors is much faster and the overall cost of a multi-processor system is cheaper.
The Good
Multicore systems have impressive performance. The first multicore processors had two cores, but current designs have four, six, eight, or higher. A processor with eight cores can execute eight different programs at the same time. Or, when faced with a computationally intense problem like matrix math, code breaking, or scientific simulation, a processor with eight cores could solve the problem eight times as fast. A desktop processor with 100 cores that can solve a problem 100 times faster is not out of reach.
In fact, modern graphics cards are already blazing this trail. Consider the 1080p standard for high definition video, which has a resolution of 1,920 × 1,080 pixels. Each pixel (short for picture element) is a dot on the screen. A screen whose resolution is 1080p has 2,073,600 dots. To maintain the illusion of smooth movement, these dots should be updated around 30 times per second. Computing the color for more than 2 million dots based on 3D geometry, lighting, and physics effects 30 times a second is no easy feat. Some of the cards used to render computer games have hundreds or thousands of cores. These cores are not general purpose or completely independent. Instead, they’re specialized to do certain kinds of matrix transformations and floating-point computations.
The Bad
Although chip-makers have spent a lot of money marketing multicore technology, they haven’t spent much money explaining that one of the driving forces behind the “multicore revolution” is a simple failure to make processors faster in other ways. In 1965, Gordon Moore, one of the founders of Intel, remarked that the density of silicon microprocessors had been doubling every year (though he later revised this to every two years), meaning that twice as many transistors (computational building blocks) could fit in the same physical space. This trend, often called Moore’s Law, has held up reasonably well. For years, clever designs relying on shorter communication times, pipelining, and other schemes succeeded in doubling the effective performance of processors every two years.
At some point, the tricks became less effective and exponential gains in processor clock rate could no longer be sustained. As clock frequency increases, the signal becomes more chaotic, and it becomes more difficult to tell the difference between the voltages that represent 0s and 1s. Another problem is heat. The energy that a processor uses is related to the square of the clock rate. This relationship means that increasing the clock rate of a processor by a factor of 4 will increase its energy consumption (and heat generation) by a factor of 16.
The legacy of Moore’s Law lives on. We’re still able to fit more and more transistors into tinier and tinier spaces. After decades of increasing clock rate, chip-makers began using the additional silicon density to make processors with more than one core instead. Since 2005 or so, increases in clock rate have stagnated.
The Ugly
Does a processor with eight cores solve problems eight times as fast as its single core equivalent? Unfortunately, the answer is, “Almost never.” Most problems are not easy to break into eight independent pieces.
For example, if you want to build eight houses and you have eight construction teams, then you probably can get pretty close to completing all eight houses in the time it would have taken for one team to build a single house. But what if you have eight teams and only one house to build? You might be able to finish the house a little early, but some steps necessarily come after others: The concrete foundation must be poured and solid before framing can begin. Framing must be finished before the roof can be put on. And so on.
Like building a house, most problems you can solve on a computer are difficult to break into concurrent tasks. A few problems are like painting a house and can be completed much faster with lots of concurrent workers. Other tasks simply cannot be done faster with more than one team on the job. Worse, some jobs can actually interfere with each other. If a team is trying to frame the walls while another team is trying to put the roof onto unfinished walls, neither will succeed, the house might be ruined, and people could get hurt.
On a desktop computer, individual cores generally have their own level 1 cache but share level 2 cache and RAM. If the programmer isn’t careful, he or she can give instructions to the cores that will make them fight with each other, overwriting memory that other cores are using and crashing the program or giving an incorrect answer. Imagine if different parts of your brain were completely independent and fought with one another. The words that came out of your mouth might be gibberish.
To recap, the first problem with concurrent programming is finding ways to break down problems so that they can be solved faster with multiple cores. The second problem is making sure that the different cores cooperate so that the answer is correct and makes sense. These are not easy problems, and many researchers are still working on finding better ways to do both.
Some educators believe that beginners will be confused by concurrency and should wait until later courses to confront these problems. We disagree: Forewarned is forearmed. Concurrency is an integral part of modern computation, and the earlier you get introduced to it, the more familiar it’ll be.
1.5. Summary
This introductory chapter focused on the fundamentals of a computer. We began with a description of computer hardware, including the CPU, memory, and I/O devices. We also described the software of a computer, highlighting key programs such as the operating system and compilers as well as other useful programs like business applications, video games, and web browsers.
Then, we introduced the topic of how numbers are represented inside the computer. Various number systems and conversion from one system to another were explained. We discussed how floating-point representation is used to represent rational numbers. A sound knowledge of data representation helps a programmer decide what kind of data to use (integer or floating-point and how much precision) as well as what kind of errors to expect (overflow, underflow, and floating-point precision errors).
The next chapter extends the idea of data representation into the specific types of data that Java uses and introduces representation systems for individual characters and text.
1.6. Exercises
Conceptual Problems
-
Name a few programming languages other than Java.
-
What’s the difference between machine code and bytecode?
-
What are some advantages of JIT compilation over traditional, ahead-of-time compilation?
-
Without converting to decimal, how can one find out whether a given binary number is odd or even?
-
Convert the following positive binary numbers into decimal.
-
1002
-
1112
-
1000002
-
1111012
-
101012
-
-
Convert the following positive decimal numbers into binary.
-
1
-
15
-
100
-
1,025
-
567,899
-
-
What’s the process for converting the representation of a binary integer given in one’s complement into two’s complement?
-
Perform the conversion from one’s complement to two’s complement on the representation
1011 0111, which uses 8 bits for storage. -
Convert the following decimal numbers to their hexadecimal and octal equivalents.
-
29
-
100
-
255
-
382
-
4,096
-
-
Create a table that lists the binary equivalents of octal digits, similar to the one in Section 1.3.2.4. Hint: Each octal digit can be represented as a sequence of three binary digits.
-
Use the table from Exercise 1.10 to convert the following octal numbers to binary.
-
3378
-
248
-
7778
-
-
The ternary number system has a base of 3 and uses symbols 0, 1, and 2 to construct numbers. Convert the following decimal numbers to their ternary equivalents.
-
23
-
333
-
729
-
-
Convert the following decimal numbers to 8-bit, two’s complement binary representations.
-
-15
-
-101
-
-120
-
-
Given the following 8-bit binary representations in two’s complement, find their decimal equivalents.
-
1100 0000 -
1111 1111 -
1000 0001
-
-
Perform the following arithmetic operation on the following 8-bit, two’s complement binary representations of integers. Check your answers by performing arithmetic on equivalent decimal numbers.
-
0000 0011+0111 1110= -
1000 1110+0000 1111= -
1111 1111+1000 0000= -
0000 1111-0001 1110= -
1000 0001-1111 1100=
-
-
Extrapolate the rules for decimal and binary addition to rules for the hexadecimal system. Then, use these rules to perform the following additions in hexadecimal. Check your answers by converting the values and their sums to decimal.
-
A2F16 + BB16 =
-
32C16 + D11F16 =
-
-
Expand Example 1.14 assuming that you have ten bits to represent the fraction. Convert the representation back to base 10. How far off is this value from 0.3?
-
Will the process in Example 1.14 ever terminate, assuming that we can use as many bits as needed to represent 0.3 in binary? Why or why not?
-
Derive the binary representation of the following decimal numbers assuming 32-bit (single) precision representation using the IEEE 754 floating-point format.
-
0.0125
-
7.7
-
-10.3
-
-
The IEEE 754 standard also defines a 16-bit (half) precision format. In this format there is one sign bit, five bits for the exponent, and ten bits for the mantissa. This format is the same as single and double precision in that it assumes that a bit with a value of 1 precedes the ten bits in the mantissa. It also uses a bias of 15 for the exponent. What’s the largest decimal number that can be stored in this format?
-
Let a, b, and c denote three real numbers. With real numbers, each of the equations below is true. Now suppose that all arithmetic operations are performed using floating-point representations of these numbers. Indicate which of the following equations are still always true and which are sometimes false.
-
(a + b) + c = a + (b + c)
-
a + b = b + a
-
a · b = b · a
-
a + 0 = a
-
(a · b) · c = a · (b · c)
-
a · (b + c) = (a · b) + (a · c)
-
-
What’s a multicore microprocessor? Why do you think a multicore chip might be better than a single core chip? Search the Internet to find the specifications for a few common multicore chips. Which chip does your computer use?
2. Problem Solving and Programming
If you can’t solve a problem, then there is an easier problem you can solve: find it.
2.1. Problem: How to solve problems
How do we solve problems in general? This question is the motivating problem (or meta-problem, even) for this chapter. In fact, this question is the motivating problem for this book. We want to understand the process of solving problems with computers.
As we mentioned in the previous chapter, many computer programs such as business applications and web browsers have already been created to help people solve problems, but we want to solve new problems by writing our own programs. The art of writing these programs is called computer programming or just programming.
Many people reading this book will be computer science students, and that’s great. However, computers have found their way into every segment of commercial enterprise and personal life. Consequently, programming has become a general-purpose skill that can aid almost anyone in their career, whether it’s in transportation, medicine, the military, commerce, or innumerable other areas.
2.1.1. What is a program?
If you don’t have a lot of experience with computer science, writing a computer program may seem daunting. The programs that run on your computer are complex and varied. Where would you start if you wanted to create something like Microsoft Word or Adobe Photoshop?
A computer program is a sequence of instructions that a computer follows. Even the most complex program is just a list of instructions. The list can get very long, and the computer can jump around the list when it makes decisions about what to do next.
Researchers continue to make progress in the field of artificial intelligence, but there is still an enormous gulf between artificial intelligence and human intelligence. Furthermore, it is the software whose intelligence those researchers strive to improve. Computer hardware is neither smart nor stupid because a computer has no intelligence to measure. A computer is a machine like a sewing machine or an internal combustion engine. It follows the instructions we give it blindly. It doesn’t have feelings or opinions about the instructions it receives. Computers do exactly what we tell them to and rarely make mistakes.
Once in a while, a computer will make a mistake due to faulty construction, a bad power source, or cosmic rays, but well over 99.999% of the things that go wrong with computers are because some human somewhere gave a bad instruction. This point highlights one of the most challenging aspects of programming a computer. How do you organize your thoughts so that you express to the computer exactly what you want it to do? If you give a person directions to a drug store, you might say, “Walk east for two blocks and then go into the third door on the right.” The human will fill in all the necessary details: Stopping for traffic, crossing at crosswalks, watching out for construction, and so on. Given a robot body, a computer would do exactly what you say. The instructions never mentioned opening the door, and so a computer might walk right through the closed door, shattering glass in the process.
2.1.2. What is a programming language?
What’s the right level of detail for instructions for a computer? It depends on the computer and the application. But how do we give these instructions? Programs are composed of instructions written in a programming language. In this book, we will use the Java programming language.
Why can’t the instructions be given in English or some other natural language? If the previous example of a robot walking through a glass door didn’t convince you, consider the quote from Groucho Marx, “One morning I shot an elephant in my pajamas. How he got into my pajamas, I’ll never know.”
Natural languages are filled with idioms, metaphors, puns, and other ambiguities. Good writers use these to give life to their poetry and prose, but our goal in this book is not to write poetry or prose. We want to write crystal clear instructions for computers.
Learning Java is not like learning Spanish or Swahili. Like most programming languages, Java is highly structured. It has fewer than 100 reserved words and special symbols. There are no exceptions to its grammatical rules. Don’t confuse the process of designing a solution to a problem with the process of implementing that solution in a programming language. Learning to organize your thoughts into a sequential list of instructions is different from learning how to translate that list into Java or another programming language, but there’s a tight connection between the two.
Learning to program is patterning your mind to think like a machine, to break everything down into simple logical steps. At first, Java code will look like gobbledygook. Eventually, it’ll become so familiar that a glance will tell you volumes about how a program works. Learning to program is not easy, but the kind of logical analysis involved is valuable even if you never program afterward. If you do need to learn other programming languages in the future, it will be easy once you’ve mastered Java.
2.1.3. An example problem
This chapter takes a broad approach to solving problems with a computer, but we need an example to make some of the steps concrete. We use the following problem from physics as an example throughout this chapter.
A rubber ball is dropped on a flat, hard surface from height h. What’s the maximum height the ball will reach after the kth bounce? We’ll discuss the steps needed to create a program to solve this problem in the next section.
2.2. Concepts: Developing software
2.2.1. Software development lifecycle
The engineers who built the first digital computers also wrote the programs for them. In those days, programming was closely tied to the hardware, and the programs were not very long. As the capabilities of computers have increased and programming languages have evolved, computer programs have grown more and more complicated. Hundreds of developers, testers, and managers are needed to write a set of programs as complex as Microsoft Windows 10.
Organizing the creation of such complicated programs is challenging, but the industry uses a process called the software development lifecycle to help. This process makes large projects possible, but we can apply it to the simpler programs we’ll write in this book as well. There are many variations on the process, but we’ll use a straightforward version with the following five steps:
-
Understand the problem: It seems obvious, but when you go to write a program, all kinds of details need to be worked out. Consider a program that stores medical records. Should the program give an error if a patient’s age is over 150 years? What if advances in long life or cryogenic storage make such a thing possible? What about negative ages? An unborn child (or more outlandishly, someone who had traveled back into the past using a time machine) could be considered to have a negative age.
Even small details like these must be carefully considered to understand a problem fully. In industry, understanding the problem is often tied to a requirements document, in which a client lays out the features and functionality that the final program should have. The “client” could also be a manager or executive officer of the company you work for who wants your development team to create a certain kind of program. Sometimes the client does not have a strong technical background and creates requirements that are difficult to fulfill or vaguely specified. The creation of the requirements document can be a negotiation process in which the software development team and their client decide together what features are desirable and reasonable.
If you’re taking a programming class, you can think of your instructor as your client. Then, you can view a programming assignment as a requirements document and your grade as your payment awarded based on how well the requirements were fulfilled.
-
Design a solution: Once you have a good grasp on the problem, you can begin to design a solution. For large scale projects, this may include decisions about the kinds of hardware and software packages that will be needed to solve the problem. For this book, we’ll only talk about problems that can be solved on standard desktop or laptop computers with Java installed.
We’ll be interested only in the steps that the computer will have to take to solve the problem. A finite list of steps taken to solve a problem is called an algorithm. If you’ve ever done long division (or any other kind of arithmetic) by hand, you’ve executed an algorithm. The steps for long division will work for any real numbers, and most human beings can follow the algorithm without difficulty.
An algorithm is often expressed in pseudocode, a high level, generic, code-like system of notation. Pseudocode is similar to a programming language, but it doesn’t have the same detail. Algorithms are often designed in pseudocode so that they aren’t tied to any one programming language.
When attacking a problem, it’s typical to break it into several smaller subproblems and then create algorithms for the subproblems. This approach is called top-down programming.
-
Implement the solution: Once you have your solution planned, you can implement it in a programming language. This step entails taking all the pseudocode, diagrams, and any other plans for your solution and translating them into code in a programming language. We use Java for our language in this book, but real developers use whichever language they feel is appropriate.
If you’ve designed your solution with several parts, you can implement each one separately and then integrate the solutions together. Professional developers often assign different parts of the solution to different programmers or even different teams of programmers.
Students are often tempted to jump into the implementation step, but never forget that this is the third step of the process. If you don’t fully understand the problem and have a plan to attack it, the implementation process can become bogged down and riddled with mistakes. At first, the problems we introduce and the programs needed to solve them will be simple. As you move into more complicated problems in this book and in your career as a programmer, a good understanding of the problem and a good plan for a solution will become more and more important.
-
Test the solution: Expressing your algorithm in a programming language is difficult. If your algorithm was wrong, your program won’t always give the right answer. If your algorithm was right but you made a mistake implementing it in code, your program will still be wrong. Programming is a very detail-oriented activity. Even experienced developers make mistakes all the time.
Good design practices help, but all code must be thoroughly tested after it’s been implemented. It should be tested exhaustively with expected and unexpected input. Tiny mistakes in software called bugs can lie hidden for months or even years before they’re discovered. Sometimes a software bug is a source of annoyance to the user, but other times, as in aviation, automotive, or medical software, people die because of bugs.
Most of this book is dedicated to designing solutions to problems and implementing them in Java, but Chapter 16 is all about testing and debugging.
-
Maintenance: Imagine you’ve gone through the previous four steps: You understood all the details of a problem, planned a solution to it, implemented that solution in a programming language, and tested it until it was perfect. What happens next?
Presumably your program is shipped to your customers and they happily use it. But what if a bug is discovered that slipped past your testing? What if new hardware comes out that’s not compatible with your program? What if your customers demand that you change one little feature?
Particularly with complex programs that have a large number of consumers, a software development company must spend time on customer support. Responsible software developers are expected to fix bugs, close security vulnerabilities, and polish rough features. This process is called maintenance. Developers are often working on the next version of the product, which could be considered maintenance or a new project entirely.
Although we cannot stress the importance of the first four steps of the software development lifecycle enough, maintenance is not something we talk about in depth.
The software development lifecycle we presented above is a good guide, but it does not go into details. Different projects require different amounts of time and energy for each step. It’s also useful to focus on the steps because it’s less expensive to fix a problem at an earlier stage in development. It’s impossible to set the exact numbers, but some developers assume that it takes ten times as much effort to fix a problem at the current step than it would have at the previous step.
Imagine that your company works on computer-aided design (CAD) software. The requirements document for a new program lists the formula for the area of a triangle as base · height when the real formula is ½ base · height. If that mistake were caught while understanding the problem, it would mean changing one line of text. Once the solution to the problem has been designed, there might be more references to the incorrect formula. Once the solution has been implemented, those references will have turned into code that is scattered throughout the program. If the project were poorly designed, several different pieces of code might independently calculate the area of a triangle incorrectly. Once the implementation has been tested, a change to the code will mean that everything has to be tested from the very beginning, since fixing one bug can cause other bugs to surface. Finally, once the maintenance stage has been reached, the requirements, plan, implementation, and testing would all need to be updated to fix the bug. Moreover, customers would already have the faulty program. Your company would have to create a patch to fix the bug and distribute it over the Internet.
Most bugs are more complicated and harder to fix, but even this simple one causes greater and greater repercussions as it goes uncaught. A factor of ten for each level implies that it takes 10,000 times more effort to fix it in the maintenance phase than at the first phase. Since fixing it at the first phase would have required a few keystrokes and fixing it in the last phase would require additional development and testing with web servers distributing patches and e-mails apologizing for the mistake, a factor of 10,000 could be a reasonable estimate.
Now that we have a sense of the software development lifecycle, let’s look at an example using the sample ball bouncing problem to walk some of its steps.
Recall the statement of the problem from the Problem section:
A rubber ball is dropped on a flat, hard surface from height h. What is the maximum height the ball will reach after the kth bounce?
-
Understand the problem: This problem requires an understanding of some physics principles. When a ball is dropped, the height of its first bounce depends on a factor known as the coefficient of restitution.
If c is the coefficient of restitution, then the ball will bounce back the first time to a height of hc. Then, we can act as if the ball were being dropped from this new height when calculating the next bounce. Thus, it will bounce to a height of hc2 the second time. By examining this pattern for the third and fourth bounce, it becomes clear that the ball will bounce to a height of hck on the kth time. See Figure 2.1 for a graphic description of this process.
We’re assuming that k > 0 and that c < 1. Note that c depends on many factors, such as the elasticity of the ball and the properties of the floor on which the ball is dropped. However, if we know that we will be given c, we don’t need to worry about any other details.
Figure 2.1 A ball is dropped from height h. The ball rises to height hc after the first bounce and to hc2 after the second. -
Design a solution: This problem is straightforward, but it’s always useful to practice good design. Remember that you’ve got to plan your input and output as well as the computation in a program. As practice for more complicated problems, let’s break this problem down into smaller subproblems.
- Subproblem 1
-
Get the values of h, c, and k from the user.
- Subproblem 2
-
Compute the height of the ball after the kth bounce.
- Subproblem 3
-
Display the calculated height.
The solution to each of the three subproblems requires input and generates an output. Figure 2.2 shows how these solutions are connected. The first box in this figure represents the solution to subproblem 1. It asks a user to input values of parameters h, c, and k. It sends these values to the next box, which represents a solution to subproblem 2. This second box computes the height of the ball after k bounces and makes it available to the third box, which represents a solution to subproblem 3. This third box displays the calculated height.
Figure 2.2 Connections between solutions to the three subproblems in the bouncing ball problem.
Before we can continue on to Step 3, we need to learn some Java. Section 2.3 introduces you to the Java you’ll need to solve this problem.
2.2.2. Acquiring a Java compiler
Before we introduce any Java syntax, you should make sure you have a Java compiler set up so that you can follow along and test your solution. Programming is a hands-on skill. It’s impossible to improve your programming abilities without practice. No amount of reading about programming is a substitute for the real thing.
Where can you get a Java compiler? Fortunately, there are free options for almost every platform. Non-Windows computers may already have the Java Runtime Environment (JRE) installed, allowing you to run Java programs; however, many Java development options require you to have the Java Development Kit (JDK). Oracle may change the website, but at the time of writing you can download the JDK from the Oracle downloads site. Download a current version (e.g., Java SE 8 or 11) of the Java Platform, Standard Edition JDK and install it.
After having done so, you should be able to compile programs using the
javac command, whose name is short for “Java compiler.” To do so,
open a terminal window, also known as a command line interface or the
console. To open the terminal in Windows, choose the Windows Powershell
option from the Start Menu. To open the
terminal in macOS, select Terminal from the Utilities folder. Different distributions of
Linux have different ways of accessing the terminal, but Linux users are usually
familiar with their terminal.
Provided that you have your path set correctly, you should be able to
open the terminal, navigate to a directory containing files that end in
.java, and compile them using the javac command. For example, to
compile a program called Example.java to bytecode, you would type:
javac Example.java
Compiling the program creates a .class file, in this case,
Example.class. To run the program contained in Example.class, you
would type:
java Example
Doing so fires up the JVM, which uses the JIT compiler to compile the
bytecode inside Example.class into machine code and run it. Note that
you type only Example not Example.class when specifying the
program to run. Using just these commands from the terminal, you can
compile and run Java programs. The command line interface used to be the
only way to interact with a computer, and though it seems primitive at
first, the command line has amazing power and versatility.
To use the command line interface to compile your own Java program, you must first create a text file with your Java code in it. The world of programming is filled with many text editor applications whose only purpose is to make writing code easier. These editors are not like Microsoft Word: They are not used to format the text into paragraphs or apply bold or italics. Their output is a “plain” text file, containing only unformatted characters, similar to the files created by Notepad. Some text editors have advanced features useful for programmers, such as syntax highlighting (marking special words and symbols in the language with colors or fonts), language-appropriate auto-completion, and powerful find and replace tools. Two of the most popular text editors for command line use are vi-based editors, particularly Vim, and Emacs-based editors, particularly GNU Emacs.
Many computer users, however, are used to a graphical user interface (GUI), where a mouse can be used to interact with windows, buttons, text boxes, and other elements of a modern user interface. There are Java programming environments that provide a GUI from which a user can write Java code, compile it, execute it, and even test and debug it. Because these tools are integrated into a single program, these applications are called integrated development environments (IDEs).
Two of the most popular Java IDEs are Eclipse and IntelliJ IDEA. Eclipse is open-source, free, and available here. Although some versions of IntelliJ IDEA cost money, the Community edition of IntelliJ IDEA is free and available here.
Which text editor or graphical IDE you use is up to you. Programming is a craft, and every artisan has favorite tools. Most of the content of this book is completely independent from the tools you use to write and compile your code. One exception is Chapter 16, in which we briefly discuss the debugging tools in Eclipse and IntelliJ IDEA.
If you choose Eclipse, IntelliJ IDEA, or another complex IDE, you may wish to read online tutorials to get started. These IDEs often require the user to make a project and then create Java files inside. The idea of a project containing related source code files is a useful one and is very common in software engineering, but it is not a part of Java itself.
2.3. Syntax: Java basics
In this section, we start with the simplest Java programs and work up to the solution to the bouncing ball problem. Syntax is the rules for constructing legal programs, just as English grammar is the rules for constructing legal English sentences. Java was first released in 1995, a long time ago in the history of computer science, but it was based on even older languages. Its syntax inherits ideas from C, C++, and other languages.
Some critics have complained about elements of the syntax or semantics of Java. Semantics are rules for what code means. Remember that Java is an arbitrary system, designed by fallible human beings. The rules for building Java programs are generally logical, but they are artificial. Learning a new programming language is a process of accepting a set of rules and coming up with ways to use those rules to achieve your own ends.
There are reasons behind the rules, but we won’t always be able to explain those reasons in this book. As you begin to learn Java, you’ll have to take it on faith that such-and-such a rule is necessary, even though it seems useless or mysterious. In time, these rules will become familiar and perhaps sensible. The mystery will fade away, and the rules will begin to look like an organic and logical (though imperfect) system.
2.3.1. Java program structure
The first rule of Java is that all code goes inside of a class. A class is a container for blocks of code called methods, and it can also be used as a template to create objects. We’ll talk a bit more about classes in this chapter and then focus on them heavily in Chapter 9.
For now, you only need to remember that every Java program has at least
one class. It is possible to put more than one class in a file, but you
can only have one top-level public class per file. A public class is
one that can be used by other classes. Almost every class in this book
is public, and they should be clearly marked as such. To create a public
class called Example, you would type the following:
public class Example {
}A few words in Java have a special meaning and cannot be used for
other purposes (like the name you give a class). These are called keywords or
reserved words. The keyword public marks the class as public. The
keyword class states that you are declaring a class. All keywords are lowercase in Java.
The name Example gives the name of the class. By convention, all class names
start with a capital letter. The braces ({ and }) mark the start
and end of the contents of the class. Right now, our class contains
nothing.
This text should be saved in a file called Example.java. It’s
required that the name of the public class matches the file that it’s
in, including capitalization. Once Example.java has been saved, you
can compile it into bytecode. However, since there’s nothing in class
Example, you can’t run it as a program.
A program is a list of instructions, and that list has to start
somewhere. For a normal Java application, that place is the main()
method. Throughout this book, we always append parentheses () to mark
the name of a method. If we want to do something inside of Example,
we’ll have to add a main() method like so:
public class Example {
public static void main(String[] args) {
}
}There are several new items now. As before, public means that other
classes can use the main() method. The static keyword means that the
method is associated with the class as a whole and not a particular
object. The void keyword means that the method does not give back a result.
The word main is obviously the name of the method, but it has
to be spelled exactly that way (including capitalization) to work.
Perhaps the most confusing part is the expression String[] args, which
is a list of text (strings) given as input to the main() method from
the command line. As with the class, the braces mark the start and end
of the contents of the main() method, which is currently empty.
Right now, you don’t need to understand any of this. All you need to
know is that, to start a program, you need a main() method and its
syntax is always the same as the code listed above. If you save this
code, you can compile Example.java and then run it, and…nothing
happens! It’s a perfectly legal Java program, but the list of
instructions is empty.
2.3.2. Command line input and output
An important thing for a Java program to do is to communicate with the outside world (where humans live). First, let’s look at printing data to the command line and reading data in from the command line.
The System.out.print() method
Methods allow us to perform actions in Java. They are blocks of code packaged up with a name so that we can run the same piece of code repeatedly but with different inputs. We discuss them in much greater depth in Chapter 8.
A common method for output is System.out.print(). The input (usually
called arguments) to a method are given between its parentheses. Thus,
if we want to print 42 to the terminal, we type:
System.out.print(42);Note that the use of the method has a semicolon (;) after it. An
executable line of code in Java generally ends with a semicolon to
separate it from the next instruction. We can add this code to our
Example class, yielding:
public class Example {
public static void main(String[] args) {
System.out.print(42);
}
}If we want to print out text, we give it as the argument to
System.out.print(), surrounded by double quotes ("). It’s necessary
to surround text with quotes so that Java knows it’s text and not the
name of a class, method, or variable. Text surrounded by double quotes
is called a string. The following program prints Forty two onto the
terminal.
public class Example {
public static void main(String[] args) {
System.out.print("Forty two");
}
}Printing out one thing is great, but programs are usually composed of many instructions. Consider the following program:
public class Example {
public static void main(String[] args) {
System.out.print(2);
System.out.print(4);
System.out.print(6);
System.out.print(8);
}
}As you can see, each executable line ends with a semicolon, and they are
executed in sequence. This code prints 2, 4, 6, and 8 onto the screen.
However, we did not tell the program to move the cursor to a new line at
any point so the output on the screen is 2468, which looks like a
single number. If we want them to be on separate lines, we can achieve
this with the System.out.println() method, which moves to a new line
after it finishes output.
public class Example {
public static void main(String[] args) {
System.out.println(2);
System.out.println(4);
System.out.println(6);
System.out.println(8);
}
}This change makes the output into the following:
2 4 6 8
In Java, it’s possible to insert math almost anywhere. Consider
the following program, which uses the + operator.
public class Example {
public static void main(String[] args) {
System.out.print(35 + 7);
}
}This code prints out 42 to the terminal just like our earlier example,
because it does the addition before giving the result to
System.out.print() for output.
The Scanner class
We want to be able to read input from the user as well. For command line
input, we need to create a Scanner object. This object is used to read
data from the keyboard. The following program asks the user for an
integer, reads in an integer from the keyboard, and then prints out the
value multiplied by 2.
import java.util.Scanner;
public class Example {
public static void main(String[] args) {
Scanner in;
in = new Scanner(System.in);
System.out.print("Enter an integer: ");
int value;
value = in.nextInt();
System.out.print("That number doubled is: ");
System.out.println(value * 2);
}
}This program introduces several new elements. First, note that it begins
with
import java.util.Scanner;. This line of code tells the compiler to use
the Scanner class that is in the java.util package. A package is a
way of organizing a group of related classes. Someone else wrote the
Scanner class and all the other classes in the java.util package,
but by importing the package, we’re able to use their code in our
program.
Then, skip down to the first line in the main() method. The code
Scanner in; declares a variable called in with type Scanner.
A variable can hold a value. The variable has a specific type, meaning
the kind of data that the value can be. In this case the type is
Scanner, meaning that the variable in holds a Scanner object.
Declaring a variable creates a box that can hold things of the specified
type. To declare a variable, first put the type you want it to have,
then put its identifier or name, and then put a semicolon. We chose to
call the variable in, but we could have called it input or even
marmalade if we wanted. It’s always good practice to name your
variable so that it’s clear what it contains.
The next line assigns a value to in. The assignment operator (=)
looks like an equal sign from math, but think of it as an arrow that
points left. Whatever’s on the right side of the assignment operator
will be stored into the variable on the left. The variable in was
an initially empty box that could hold a Scanner object. The code
new Scanner(System.in) creates a brand new Scanner object based on
System.in, which means that the input will be from the keyboard. The
assignment stored this object into the variable in. The fact that
System.in was used has nothing to do with the fact that our variable
was named in. Again, don’t expect to understand all the details at
first. Any time you need to read data from the keyboard, you’ll need
these two lines of code, which you should be able to copy verbatim. It’s
possible to both declare a variable and assign its value in one line.
Instead of the two line version, most programmers would type:
Scanner in = new Scanner(System.in);Similarly, the line int value; declares a variable for holding integer
types. The next line uses the object in to read an integer from the
user by calling the nextInt() method. If we wanted to read a floating-point
value, we would have called the nextDouble() method. If we
wanted to read some text, we would have called the next() method.
Unfortunately, these differences means that we have to know what type of
data the user is going to enter. If the user enters an unexpected type,
our program could have an error. As before, we could combine the
declaration and the assignment into a single line:
int value = in.nextInt();The final two lines give output for our program. The former prints
That number doubled is: to the terminal. The latter prints out a
value that is twice whatever the user entered. The next two examples
illustrate how Scanner can be used to read input while solving
problems. The first example shows how these elements can be applied to
subproblem 1 of the bouncing ball problem, and the second example
introduces and solves a new problem.
Subproblem 1 requires us to get the height, coefficient of restitution, and number of bounces from the user. Program 2.1 shows a Java program to solve this subproblem.
import java.util.*; (1)
public class GetInputCLI { (2)
public static void main(String[] args) { (3)
// Create an object named in for input
Scanner in = new Scanner(System.in); (4)
// Declare variables to hold input data
double height, coefficient; (5)
int bounces;
// Prompt the user and read data from the keyboard
System.out.println("Bouncing Ball: Subproblem 1"); (6)
System.out.print("Enter the height: ");
height = in.nextDouble(); (7)
System.out.print("Enter restitution coefficient: "); (8)
coefficient = in.nextDouble();
System.out.print("Enter the number of bounces: ");
bounces = in.nextInt();
}
}| 1 | Unlike our earlier example, the first line of GetInputCLI.java is
import java.util.*;. Instead of importing only the Scanner class,
this line imports all the classes in the java.util package. The
asterisk (*) is known as a wildcard. The wildcard notation is
convenient if you need to import several classes from a package or if
you don’t know in advance the names of all the classes you’ll need. |
| 2 | The class declaration names the class GetInputCLI. We put a CLI at the end of the name to mark that
it uses the command line interface, contrasting with the GUI version that we’re going to show next. |
| 3 | Inside the class declaration is the
definition of the main() method, showing where the program starts. The text that comes after double slashes (//) is called a comment. Comments allow us to make our code more readable to humans, but the
compiler ignores them. |
| 4 | After the comments, we declare and instantiate a Scanner variable called in for reading from the keyboard. |
| 5 | Next, we declare two double
variables (for holding double precision floating-point numbers) and an
int variable (for holding an integer value). |
| 6 | We print out the name of the problem and then print out "Enter the height: ". |
| 7 | The line height = in.nextDouble(); tries to read in the height from the user. It waits until the user hits enter before reading the value and moving on to the next line. |
| 8 | The last four lines of the program prompt and read in the coefficient of restitution and then the number of bounces. If you compile and run this program, the execution should match the steps described. Note that it only reads in the values needed to solve the problem. We haven’t added the code to compute the answer or display it. |
Let’s write a program that takes as input the speed of a moving object and the time it’s been moving. The goal is to compute and display the total distance it travels. We can divide this problem into the following three subproblems.
- Subproblem 1
-
Input speed and duration.
- Subproblem 2
-
Compute distance traveled.
- Subproblem 3
-
Display the computed distance.
Program 2.2 solves each of these subproblems in order, using the command-line input and output tools we have just discussed.
import java.util.*; (1)
public class Distance {
public static void main(String[] args) {
// Create an object named in for input
Scanner in = new Scanner(System.in); (2)
double speed, time;
double distance; // Distance to be computed
// Solution to subproblem 1: Read input
// Prompt the user and get speed and time
System.out.print("Enter the speed: "); (3)
speed = in.nextDouble();
System.out.print("Enter the time: ");
time = in.nextDouble();
// Solution to subproblem 2: Compute distance
distance = speed*time; (4)
// Solution to subproblem 3: Display output
System.out.print("Distance traveled: "); (5)
System.out.print( distance );
System.out.println(" miles.");
}
}| 1 | The program starts with import statements, the class definition, and the
definition of the main() method. |
| 2 | At the beginning of the main()
method, we have code to declare and initialize a variable of type
Scanner named in. We also declare variables of type double to hold
the input speed and time and the resulting distance. |
| 3 | We start solving subproblem 1, prompting the user for the speed and the time and using our Scanner object to read them in. Because they are both floating-point values with type double, we use the nextDouble() method for input. |
| 4 | We compute the distance traveled by multiplying speed by time and storing the result in
distance. |
| 5 | The last three lines of the main() method solve subproblem 3 by outputting "Distance traveled: ", the computed distance, and " miles.". If you run the program, all three items are printed on the same line on the terminal. |
2.3.3. GUI input and output
If you’re used to GUI-based programs, you might wonder how to do input and output with a GUI instead of on the command line. GUIs can become complex, but in this chapter we introduce a simple way to do GUI input and output and expand on it further in Chapter 7. Then, we go into GUIs in much more depth in Chapter 15.
A limited tool for displaying output and reading input with a GUI is the
JOptionPane class. This class has a complicated method called
showMessageDialog() that opens a small dialog box to display a
message to the user. If we want to create the equivalent of the
command-line program that displays the number 42, the code would be as
follows.
import javax.swing.JOptionPane; (1)
public class Example {
public static void main(String[] args) {
JOptionPane.showMessageDialog(null, "42", "Output Example", (2)
JOptionPane.INFORMATION_MESSAGE);
}
}| 1 | Like Scanner, we need to import JOptionPane as shown above in order
to use it. |
| 2 | The showMessageDialog() method takes several arguments to
tell it what to do. For our purposes, the first one is always the
special Java literal null, which represents an empty value. The next
is the message you want to display, but it has to be text. That’s why
"42" appears with quotation marks. The third argument is the title
that appears at the top of the dialog. The final argument gives
information about how the dialog should be presented.
JOptionPane.INFORMATION_MESSAGE is a flag values that specifies that
the dialog is giving information (instead of a warning or a question),
causing an appropriate, system-specific icon to be displayed on the
dialog. |
Figure 2.3 shows what the resulting GUI might look like.
showMessageDialog() used for output.One way to do input with a GUI uses the showInputDialog() method,
which is also inside the JOptionPane class. The showInputDialog()
method returns a value. This means it gives back an answer which
you can store into a variable by putting the method call on the right
hand side of an assignment statement. Otherwise, it’s nearly the same
as showMessageDialog(). The following program prompts the user for his
or her favorite word with a showInputDialog() method and then displays
it again using a showMessageDialog() method.
import javax.swing.JOptionPane;
public class Example {
public static void main(String[] args) {
String message = "What is your favorite word?";
String title = "Input Example";
String word =
JOptionPane.showInputDialog(null, message, title, JOptionPane.QUESTION_MESSAGE);
JOptionPane.showMessageDialog(null, word, title, JOptionPane.INFORMATION_MESSAGE);
}
}Note that whatever the user typed in will be stored in word. Finally,
the last line of the program displays this information with
showMessageDialog(). Figure 2.4 shows the
GUI as the user is entering input.
showInputDialog() used for input.Remember that the value returned from the showInputDialog() method is
always text; that is, it always has type String. Although there are
lots of great things you can do with a String value, you can’t do
normal arithmetic like you can with an integer or a floating-point
number. However, there are ways to convert a String representation of
a number to the number itself. If you have a String that represents an
integer, you use the Integer.parseInt() method to convert it. If you
have a String that represents a floating-point number, you use the
Double.parseDouble() method to convert it. The following segment of
code illustrates these issues.
// Text cannot be multiplied by an integer
int x = "41" * 3;
// Correctly converts the text "23" to the integer 23
int y = Integer.parseInt("23");
// Correctly converts the text "3.14159" to 3.14159
double z = Double.parseDouble("3.14159");
// Causes the program to crash
int a = Integer.parseInt("Twenty three");
// Causes the program to crash
double b = Double.parseDouble("pi");You might wonder why the computer isn’t smart enough to know that "23"
means 23. Remember, the computer has no intelligence. If something is
marked as text, it doesn’t know that it can interpret it as a number.
What kind of data something is depends on its type, which doesn’t
change. We’ll discuss types more deeply in Chapter 3.
The next example uses these two type conversion methods with methods
from JOptionPane in a GUI-based solution to subproblem 1 of the
bouncing ball problem.
We can change the solution given in Program 2.1 to
use the GUI-based input tools in JOptionPane.
Program 2.3 is the equivalent GUI-based Java program.
import javax.swing.*;
public class GetInputGUI {
public static void main(String[] args) {
String title = "Bouncing Ball: Subproblem 1";
// Declare variables to hold input data
double height, coefficient;
int bounces;
// Prompt the user, get data, and convert it
String response = JOptionPane.showInputDialog(null, (1)
"Enter the height: ", title, JOptionPane.QUESTION_MESSAGE);
height = Double.parseDouble(response); (2)
response = JOptionPane.showInputDialog(null, (3)
"Enter restitution coefficient: ", title, JOptionPane.QUESTION_MESSAGE);
coefficient = Double.parseDouble(response);
response = JOptionPane.showInputDialog(null,
"Enter the number of bounces: ", title,
JOptionPane.QUESTION_MESSAGE);
bounces = Integer.parseInt(response);
}
}| 1 | At this point the code uses the showInputDialog() method to read a String version of the height from the user. |
| 2 | On the next line, we have to
convert this String version into the double version that we store in
the height variable. |
| 3 | The next four lines read in the coefficient of restitution and the number of bounces and convert them to their appropriate numerical types. |
2.3.4. A few operations
Basic math
To make our code useful, we can perform operations on values and
variables. For example, we used the expression 35 + 7 as an argument
to the System.out.print() method to print 42 to the screen. We can
use the add (+), subtract (-), multiply (*), and divide(/)
operators on numbers to solve arithmetic problems. These operators work
the way you’d expect them to (except that division has a few surprises).
We’ll go into these operators and others more deeply in
Chapter 3. Here are examples of
these four operators used with integer and floating-point numbers.
int a = 2 + 3; // a will hold 5
int b = 2 - 3; // b will hold -1
int c = 2 * 3; // c will hold 6
int d = 2 / 3; // d will hold 0 (explained later)
double x = 1.6 + 3.2; // x will hold 4.8
double y = 1.6 - 3.2; // y will hold -1.6
double z = 1.6 * 3.2; // z will hold 5.12
double w = 1.6 / 3.2; // w will hold 0.5Other operations
These basic operations can mix values and variables together. As we’ll
discuss later, they can be arbitrarily complicated with order of
operations determining the final answer. Nevertheless, we also need ways
to accomplish other mathematical operations such as raising a number to
a power or finding its square root. The Math class has methods that
perform these and other functions. To raise a number to a power, we call
Math.pow() with two arguments: first the base and then the exponent.
To find a square root, we pass a number to the Math.sqrt() method.
// Raises 3.0 to the power 2.5, approximately 15.588457
double p = Math.pow(3.0, 2.5);
// Finds the square root of 2.0, approximately 1.4142136
double q = Math.sqrt(2.0);We compute the final height of the ball in subproblem 2 of the bouncing
ball problem. To do so, we have to multiply the height by the
coefficient of restitution raised to the power of the number of bounces.
The following program does so, using the Math.pow() method.
public class ComputeHeight {
public static void main(String[] args) {
// Use dummy values to test subproblem 2
double height = 15, coefficient = 0.3;
int bounces = 10;
// Compute height after bounces
double bounceHeight = height*Math.pow(coefficient,bounces);
System.out.println(bounceHeight); // For testing
}
}Program 2.4 is only focusing on subproblem 2, but,
if we want to test it, we need to supply some dummy values for height,
coefficient, and bounces, since these are read in by the solution to
subproblem 1. Likewise, the output statement on the last line of the
main() method is just for testing purposes. The complete solution has
more complex output.
String concatenation
Just as we can add numbers together, we can also “add” pieces of text
together. In Java, text has the type String. If you use the +
operator between two values or variables of type String, the result is
a new String that is the concatenation of the two previous String
values, meaning that the result is the two pieces of text pasted
together, one after the other. Concatenation doesn’t change the String
values you’re concatenating.
The results may be illegal or at least unexpected if you mix types (String, int,
double) together when doing mathematical operations. However, feel
free to concatenate String values with any other type using the +
operator. When you do so, the other type is automatically converted into
a String. This behavior is useful since any String is easy to
output. Here are a few examples of String concatenation.
String word1 = "tomato";
String word2 = "sauce";
String text1 = word1 + word2; // text1 contains "tomatosauce"
String text2 = word1 + " " + word2; // text2 contains "tomato sauce"
String text3 = "potato " + word1; // text3 contains "potato tomato"
String text4 = 5 + " " + word1 + "es"; // text4 contains "5 tomatoes"With String concatenation, subproblem 3 becomes a bit easier. We
concatenate the results together with an appropriate message and then
use the System.out.println() method for output.
public class DisplayHeightCLI {
public static void main(String[] args) {
// Use dummy values to test subproblem 3
int bounces = 10;
double bounceHeight = 2.0;
String message = "After " + bounces +
" bounces the height of the ball is: " + bounceHeight + " feet";
System.out.println(message);
}
}Program 2.5 is only focusing on subproblem 3,
but if we want to test it, we need to supply dummy values for bounces
and bounceHeight, since these are generated by the solution to earlier
subproblems.
The same concatenation can be used for GUI output as well. The only
difference is the use of
JOptionPane.showMessageDialog() instead of System.out.println().
import javax.swing.*;
public class DisplayHeightGUI {
public static void main(String[] args) {
String title = "Bouncing Ball: Subproblem 3";
// Use dummy values to test subproblem 3
int bounces = 10;
double bounceHeight = 2.0;
String message = "After " + bounces +
" bounces the height of the ball is: " + bounceHeight + " feet";
JOptionPane.showMessageDialog(null, message, title,
JOptionPane.INFORMATION_MESSAGE);
}
}2.3.5. Java formatting
Writing good Java code has some similarities to writing effectively in English. There are rules you have to follow in order to make sense, but there are also guidelines you should follow to make your code easier to read for yourself and everyone else.
Variable and class naming
Java programs are filled with variables, and each variable should be named to reflect its contents. Variable names are essentially unlimited in length (although the JVM you use may limit this length to thousands of characters). A tremendously long variable name can be hard to read, but abbreviations can be worse. You want the meaning of your code to be obvious to others and to yourself when you come back days or weeks later.
Imagine you’re writing a program that sells fruit. Consider the following names for a variable that keeps track of the number of apples.
| Name | Attributes |
|---|---|
|
Too short, gives no useful information |
|
Too short, vague, could mean applications or appetizers |
|
Too short, vague, could mean center |
|
Not bad, but counting what? |
|
Too long for no good reason |
|
Very clear |
|
Concise and clear, unless there are multiple apple quantities
such as |
Mathematics is filled with one letter variables, partly because there’s
a history of writing mathematics on chalkboards and paper. Clarity is
more important than brevity with variables in computer programs. Some
variables need more than one word to be descriptive. In that case,
programmers of Java are encouraged to follow camel case. In camel
case, multi-word variables and methods start with a lowercase letter and
then use an uppercase letter to mark the beginning of each new word. It’s
called camel case because the uppercase letters are reminiscent of
the humps of a camel. Examples include lastValue, symbolTable, and
makeHamSandwich().
By convention, class names should always begin with a capital letter,
but they also use camel case, marking the beginning of
each new word with an uppercase letter. Examples include LinkedList, JazzPiano, and
GlobalNuclearWarfare.
Another convention is that constants, variables whose values never
change, have names in all uppercase, separated by underscores. Examples
include PI, TRIANGLE_SIDES, and
UNIVERSAL_GRAVITATIONAL_CONSTANT.
Spaces are not allowed in variable, method, or class names. Recall that
a name in Java is called an identifier. The rules for identifiers
specify that they must start with an uppercase or lowercase letter (or
an underscore) and that the remaining characters must be letters,
underscores, or numerical digits. Thus, Tupac and
the absurd _5 are legal identifiers, but Motley Crue and
2Pac are not.
In Java, letters can mean more than just the Latin letters A through Z.
Java has support for many of the world’s languages,
allowing identifiers to contain characters from Chinese, Thai,
Devanagari, Cyrillic, and other scripts. For example, m\u00F6tleyCr\u00FCe
is a legal variable name because \u00F6 is way of encoding ö and
\u00FC is a way of encoding ü. In some systems, this variable name might
be rendered mötleyCrüe, but the compiler could complain if you type those characters in directly. In short, Java supports a huge range of
characters, but making that support work for you is sometimes more challenging.
Section 3.3.2.10 discusses character encoding further.
Remember that keywords also cannot be used as identifiers. For example,
public, static, and class are all keywords in Java and can never
be the names of classes, variables, or methods.
White space
Although you are not allowed to have spaces in a Java identifier, you can usually use white space (spaces, tabs, and new lines) wherever you want. Java ignores extra space. Consider the following line of code.
int x = y + 5;It’s equivalent to the next one.
int x=y+5;We chose to type our earlier example of a program performing output as follows.
public class Example {
public static void main(String[] args) {
System.out.print(42);
}
}However, we could have been more chaotic with our use of whitespace.
public
class Example {
public
static void
main (String [
] args
) {
System.
out
.print(42
) ; } }Or we could have used almost no whitespace at all.
public class Example{public static void main(String[]args){System.out.print(42);}}These three programs are identical in the eyes of the Java compiler, but the first one is easier for a human to read. You should use whitespace to increase readability. Don’t add too much whitespace with lots of blank lines between sections of code. On the other hand, don’t use too little and cramp the code together. Whenever code is nested inside of a set of braces, indent the contents so that it’s easy to see the hierarchical relationship.
The style we present in this book puts the left brace ({) on the line
starting a block of code. Another popular style puts the left brace on
the next line. Here is the same example program formatted in this style:
public class Example
{
public static void main(String[] args)
{
System.out.print(42);
}
}There are people (including some authors of this book) who prefer this style because it’s easier to see where blocks of code begin and end. However, the other style uses less space, so we use it throughout the book. You can make your own choices about style, but be consistent! If you work for a software development company, they may have strict standards for code formatting.
Comments
As we mentioned before, you can leave comments in your code whenever you
want someone reading the code to have extra information. Java has three
different kinds of comments. We described single-line comments, which
start with a // and continue until the end of the line.
If you have a large block of text you want as a comment, you can create
a block comment, which starts with a /* and continues until it reaches
a */.
Beyond leaving messages for other programmers, you can also “comment out” existing code. By putting Java code inside a comment, it no longer affects program execution. This practice is common when programmers want to remove or change some code but are reluctant to delete it until the new version of the code has been tested. Don’t overuse the practice of commenting out code! Large programs become hard to navigate when they’re cluttered with many chunks of commented-out code.
The third kind of comment is called a documentation comment and
superficially looks a lot like a block comment. A documentation comment
starts with a /** and ends with a */. These comments are supposed to
come at the beginning of classes and methods and explain what they’re
used for and how to use them. A tool called javadoc is used to run
through documentation comments and generate an HTML file that users can
read to understand how to use the code. This tool is a feature
that has contributed greatly to the popularity of Java, keeping its
libraries well-documented and easy to use. However, we do not
discuss documentation comments deeply in this book.
Here is our example output program, heavily commented.
/**
* Class Example prints the number 42 to the screen.
* It contains an executable main() method.
*/
public class Example {
/*
* The main() method was last updated by Barry Wittman.
*/
public static void main(String[] args) {
System.out.print(42); // answer to everything
}
}Comments are a wonderful tool, but clean code with meaningful variable names and careful use of whitespace doesn’t require too much commenting. Never hesitate to comment, but always ask yourself if there is a way to write the code so clearly that a comment is unnecessary.
2.4. Solution: How to solve problems
The problem solving steps given in Section 2.2 are sound, but they depend on being able to implement your planned solution in Java. In this chapter we have introduced far too little Java to expect to solve all the problems that can be solved with a computer. However, we can show the solution to the bouncing ball problem and explain how our solution works through the software development lifecycle.
2.4.1. Bouncing ball solution (command line version)
In Example 2.2, we made sure we understood the problem and then formed a three-part plan to read in the input, compute the height of the bounce, and then output it.
In Program 2.1, we implemented subproblem 1, reading the input from the command line. In Program 2.4, we implemented subproblem 2, computing the height of the final bounce. In Program 2.5, we implemented subproblem 3, displaying the height that was computed. In the final, integrated program, the portion of the code that corresponds to solving subproblem 1 is below.
import java.util.*;
public class BouncingBallCLI {
public static void main(String[] args) {
// Solution to subproblem 1
// Create an object named in for input
Scanner in = new Scanner(System.in);
// Declare variables to hold input data
double height, coefficient;
int bounces;
System.out.println("Bouncing Ball");
// Prompt the user and read data from the keyboard
System.out.println("Bouncing Ball: Subproblem 1");
System.out.print("Enter the height: ");
height = in.nextDouble();
System.out.print("Enter restitution coefficient: ");
coefficient = in.nextDouble();
System.out.print("Enter the number of bounces: ");
bounces = in.nextInt();With the imports, class declaration, and main() method set up by the
solution to subproblem 1, the solution to subproblem 2 is very short.
// Solution to subproblem 2
double bounceHeight = height*Math.pow(coefficient,bounces);The solution to subproblem 3 and the braces that mark the end of the
main() method and then the end of the class only take up a few
more lines.
// Solution to subproblem 3
String message = "After " + bounces +
" bounces the height of the ball is: " + bounceHeight + " feet";
System.out.println(message);
}
}2.4.2. Bouncing ball solution (GUI version)
If you prefer a GUI for your input and output, we can integrate the GUI-based versions of the solutions to subproblems 1, 2, and 3 from Program 2.1, Program 2.4, and Program 2.6. The final program is below. It only differs from the command line version in a few details.
import javax.swing.*;
public class BouncingBallGUI {
public static void main(String [] args) {
// Solution to sub-problem 1
String title = "Bouncing Ball";
double height, coefficient;
int bounces;
// Prompt the user, get data, and convert it
String response = JOptionPane.showInputDialog(null,
"Enter the height: ", title, JOptionPane.QUESTION_MESSAGE);
height = Double.parseDouble(response);
response = JOptionPane.showInputDialog(null,
"Enter restitution coefficient: ", title, JOptionPane.QUESTION_MESSAGE);
coefficient = Double.parseDouble(response);
response = JOptionPane.showInputDialog(null,
"Enter the number of bounces: ", title, JOptionPane.QUESTION_MESSAGE);
bounces = Integer.parseInt(response);
// Solution to sub-problem 2
double bounceHeight = height*Math.pow(coefficient,bounces);
// Solution to sub-problem 3
String message = "After " + bounces +
" bounces the height of the ball is: " + bounceHeight + " feet";
JOptionPane.showMessageDialog(null,
message, title, JOptionPane.INFORMATION_MESSAGE);
}
}2.4.3. Testing and maintenance
Testing and maintenance are key elements of the software engineering lifecycle and often take more time and resources than the rest. However, we only discuss them briefly here.
The ball bouncing problem is not complex. There are a few obvious things to test. We should pick a “normal” test case such as a height of 15 units, a coefficient of restitution of 0.3, and 10 bounces. The height should be 15 · 0.310 = 0.0000885735. The result computed by our program should be the same, ignoring floating-point error. We can also check some boundary test cases. If the coefficient of restitution is 1, the ball should bounce back perfectly, reaching whatever height we input. If the coefficient of restitution is 0, the ball doesn’t bounce at all, and the final height should be 0.
Our code does not account for users entering badly formatted data like
two instead of 2. Likewise, our code does not detect invalid values
such as a coefficient of restitution greater than 1 or a negative number
of bounces. An industrial-grade program should. We’ll discuss testing
further in Chapter 16.
As with most of the problems we discuss in this book, issues of maintenance will not apply: we don’t have a customer base to keep happy. Even so, it’s a good thought exercise to imagine a large-scale version of this program that can solve many different kinds of physics problems. Who are likely to be your clients? What kinds of bugs are likely to creep into such a program? How would you provide bug-fixes and develop new features?
2.5. Concurrency: Solving problems in parallel
2.5.1. Parallelism and concurrency
The terms parallelism and concurrency are often confused and sometimes used interchangeably. Parallelism or parallel computing occurs when multiple computations are being performed at the same time. Concurrency occurs when multiple computations may interact with each other. The distinction is subtle since many parallel computations are concurrent and vice versa.
An example of parallelism without concurrency is two separate programs running on a multicore system. They are both performing computations at the same time, but for the most part, they aren’t interacting with each other. Concurrency issues might arise if these programs try to access a shared resource, such as a file, at the same time.
An example of concurrency without parallelism is a program with multiple threads of execution running on a single-core system. These threads will not execute at the same time as each other. However, the OS or run-time system will interleave the execution of these threads, switching back and forth between them whenever it wants to. Since these threads can share memory, they can still interact with each other in complicated and often unpredictable ways.
With multicore computers, we want good and effective parallelism, computing many things at the same time. Unfortunately, striving to reach parallelism often means struggling with concurrency and carefully managing the interactions between threads.
2.5.2. Sequential versus concurrent programming
Imagine that the evil Lellarap aliens are attacking Earth. They have sent an extensive list of demands to the world’s leaders, but only a few people, including you, have mastered their language, Lellarapian. To save the people of Earth, it’s imperative that you translate their demands as quickly as possible so world leaders can choose a course of action. If you do it alone, as illustrated in Figure 2.5(a), the Lellaraps might attack before you finish.
In order to finish the work faster, you hire a second translator whose skills in Lellarap are as good as yours. As shown in Figure 2.5(b), you divide the document into two nearly equal parts, Document A and Document B. You translate Document A, and your colleague translates Document B. When both translations are complete, you merge the two, check the translation, and send the result to the world’s leaders.

Translating the demands alone is a sequential approach. In this context, sequential mean non-parallel. Translating the demands with two people is a parallel approach. It’s concurrent as well because you have to decide how to split up the document and how to merge it back together.
If you wrote a computer program to translate the demands using the sequential approach, you’d produce a sequential program. If you wrote a computer program that uses the approach shown in Figure 2.5(b), it would be a concurrent program. A concurrent program is also referred to as a multi-threaded program. Threads are sequences of code that can execute independently and access each other’s memory. Imagine you’re one thread of execution and your colleague is another. Thus, the concurrent approach will have at least two threads. It may have more if separate threads are used to divide up the document or merge it back together.
Because we’re interested in the time the process takes, we’ve labeled different tasks in Figure 2.5 with their running times. We let ts be the time for one person to complete the translation. The times t1 through t4 mark the times needed to complete tasks 1 through 4, indicated in Figure 2.5(b).
2.5.3. Kinds of concurrency
A sequential program, like the single translator, uses a single processor on a multi-processor system or a single core on a multicore chip. To speed up the solution of a program on a multicore chip, it may be necessary to divide a problem so that different parts of it can be executed concurrently.
This process of dividing up a problem falls into the category of domain decomposition, task decomposition, or some combination of the two. In domain decomposition, we take a large amount of data or elements to be processed and divide up the data among workers that all do the same thing to different parts of the data. In task decomposition, each worker is assigned a different task that needs to be done. The following two examples explore each of these approaches.
Suppose we have an autonomous robot called the Room Rating Robot or R3. The R3 can measure the area of any home. Suppose that we want to use an R3 to measure the area of the home with two floors sketched in Figure 2.6.

One way to measure the area is to put an R3 at the entrance of the home on the first floor and give it the following instructions:
-
Initialize total area to 0
-
Find area of next room and add to total area
-
Repeat Step 2 until all rooms have been measured
-
Move to second floor
-
Repeat Step 2 until all rooms have been measured
-
Display total area
By following these steps, the R3 will systematically go through each room, measure its area, and add the value to the total area found so far. It’ll then climb up the stairs and repeat the process for the second floor. It would add up the areas from the two floors and give us the total living area of the house. This is a sequential approach for measuring the area.
Now, suppose we have two R3 robots, named R3A and R3B. We can put R3A on the first floor and R3B on the second. Both robots are then instructed to find the area of the floor they’re on using steps very similar to the ones listed above for a sequential solution. When done, we add together the answers from R3A and R3B to get the total. This is a concurrent (and also parallel) approach for measuring the living area of a home with two floors. Using two robots this way could speed up the time it takes to measure the area.
In the example above, the tasks are the same (measuring the area) but are performed on two different input domains (the floors). This type of task division is also known as domain decomposition. Here, to achieve concurrency, we take the domain of the problem (the house) and divide it into smaller subdomains (its floors). Then, each processor (or robot in this example) performs the same task on each subdomain. When done, the final answer is found by combining the answers. Running the robots on each floor is purely parallel, but combining the answers is concurrent since some interaction between the robots is necessary.
Another way of solving a problem concurrently is to divide it into fundamentally different tasks. The tasks could be executed on different processors and perhaps on different input domains. Eventually, some coordination of the tasks must be done to generate the final result. The next example illustrates such a division.
Let’s expand the problem given in Example 2.8. R3 robots can do more than just measure area. In addition to calculating the living area of a home, we want an R3 robot to check if the electrical outlets are in working condition. The robot should give us the area of the house as well as a list of electrical outlets that are not working.
This problem can be solved in a sequential manner with just one robot. One way to do so would have a robot make a first pass through all floors and rooms and compute the living area. It could then make a second pass and compile a list of electrical outlets that are not working.
A way to solve this problem concurrently is to assign R3A to measure the area and R3B to identify broken electrical outlets. Once the respective tasks are assigned, we place the robots at the entrance to the house and activate them. It’s possible that the two robots will bump into each other while working, and that’s one of the difficulties of concurrency. The burden is on the programmer to give instructions so that the robots can avoid or recover from collisions. After the robots are done, we ask R3A for the living area of the house and R3B for a list of broken outlets.
2.6. Summary
In this chapter, we introduced an approach for developing software to solve problems with a computer. A number of examples illustrated how to move from a problem statement to a complete Java program. Although we have given rough explanations of the Java programs in this chapter, we encourage you to play with each program to expand its functionality. Several exercises prompt you to do just that. It’s impossible to learn to program without actively practicing programming. Never be afraid of “breaking” the program. Only by breaking it, changing it, and fixing it will your understanding grow.
In addition to the software development lifecycle, we introduced several
building blocks of Java syntax including classes, main() methods,
import statements, and variable declarations. We also gave a preview of
different variable types (int, double, and String) and operations
that can be used with them. Material about types and operations on them
is covered in depth in the next chapter. Furthermore, we discussed input
and output using Scanner and System.out.print() for the command line
interface and JOptionPane methods for a GUI.
Finally, we introduced the notions of sequential and concurrent solutions to problems and clarified the subtle difference between parallelism and concurrency.
2.7. Exercises
Conceptual Problems
-
When solving a problem using a computer, what problem is solved by the programmer and what problem is solved by the program written by the programmer? Are they the same?
-
In Program 2.2, we declared all variables to be of type
double. How would the program behave differently if we had declared all the variables with typeint? -
What is the purpose of the statement
Scanner in = new Scanner(System.in);in Program 2.1? -
Explain the difference between a declaration and an assignment statement.
-
Is the following statement from Program 2.7 a declaration, an assignment, or a combination of the two?
String response = JOptionPane.showInputDialog(null, message, title, JOptionPane.QUESTION_MESSAGE); -
When would you prefer using the
JOptionPaneclass for output overSystem.out.print()? When might you preferSystem.out.print()to usingJOptionPane? -
Review Program 2.7 and identify all the Java keywords used in it.
-
Try to recompile Program 2.7 after removing the
importstatement at the top. Read and explain the error message generated by the compiler. -
Explain the difference between parallel and concurrent tasks. Give examples of tasks that are parallel but not concurrent, tasks that are concurrent but not parallel, and tasks that are both.
-
Refer to Figure 2.5. Suppose that you and your colleague translate from English to Lellarapian at the rate of 200 words per hour. Suppose that the list of demands contains 10,000 words.
-
Compute ts, the time for you to translate the entire document alone, assuming that, after translation, you perform a final check at the rate of 500 words per hour.
-
Now assume that the task of splitting up the document and handing over the correct part to your colleague takes 15 minutes. Also, the task of receiving the translated document from your colleague and merging with the one you translated takes another 15 minutes. After merging the two documents, you do a final check for correctness at a rate of 500 words per hour. Calculate the total time to complete the translation using this concurrent approach. Let us refer to this time as tc.
-
One way to calculate the speedup of a concurrent solution is to divide the sequential time by the concurrent time. In our case, the speedup is ts/tc. Using the values you’ve computed in (a) and (b), calculate the speedup.
-
Suppose that you have a total of two colleagues willing to help you with the translation. Assuming that the three of you will perform the translation and that the times needed to split, merge, and check are unchanged, calculate the total time needed. Then, compute the speedup.
-
Now suppose that there are an unlimited number of people willing and able to help you with the translation. Will the speedup keep on increasing as you add more translators? Explain your answer.
-
-
In Example 2.8, what aspect of a multicore system do the robots represent?
-
In Example 2.8, suppose that you have two R3 robots available. You’d like to use them to measure the living area of a single-floor home. Suggest how two robots could be programmed to work concurrently to measure the living area faster than one.
Programming Practice
-
Write a program that prompts the user for three integers from the command line. Read each integer in using the
nextInt()method of aScannerobject. Compute the sum of these values and print it to the screen usingSystem.out.print()orSystem.out.println(). -
Expand the program from Exercise 2.13 so that it finds the average of the three numbers instead of the sum. (Hint: Try dividing by
3.0instead of3to get an average with a fractional part. Then, store the result in a variable of typedouble.) -
Rewrite your solution to Exercise 2.14 so that it uses a
JOptionPane-based GUI instead ofScannerandSystem.out.print(). -
Copy and paste Program 2.1 into the Java IDE you prefer. Compile and run it and make sure that the program executes as intended. Then, add statements to prompt the user for the color of the ball and read it in. Store the color in a
Stringvalue. Add an output statement that mentions the color of the ball. -
Rewrite your solution to Exercise 2.16 so that it uses a
JOptionPane-based GUI instead ofScannerandSystem.out.print(). -
In Example 2.4, we assumed that the speed is given in miles per hour and the time in hours. Change Program 2.2 to compute the distance traveled by a moving object given its speed in miles per hour but time in seconds. You will need to perform a conversion from seconds to hours before you can find the distance.
-
A program can use both a command line interface and a GUI to interact with a user. Write a program that uses the
Scannerclass to read aStringvalue containing the user’s favorite food. Then display the name of the food usingJOptionPane. -
Use the complete software development cycle to write a program that reads in the lengths of two legs of a right triangle and computes the length of its hypotenuse.
-
Make sure you understand the problem. How can you apply the Pythagorean formula a2 + b2 = c2 to solve it?
-
Design a solution by listing the steps you will need to take to read in the appropriate values, find the answer, and then output it.
-
Implement the steps as a Java program.
-
Test the solution with several known values. For example, a right triangle with legs of lengths 3 and 4 has a hypotenuse of length 5. Which values cause errors? How should your program react to those errors?
-
Consider what other features your program should have. If your intended audience is children who are learning geometry, should your error handling be different from an audience of architects?
-
3. Primitive Types and Strings
Originality exists in every individual because each of us differs from the others. We are all primary numbers divisible only by ourselves.
3.1. Problem: College cost calculator
Perhaps you’re a student. Perhaps you aren’t. In either case, you must be aware of the rapidly rising cost of a college education. The motivating problem for this chapter is to create a Java program that can estimate this cost, including room and board. It starts by reading a first name, a last name, the per-semester cost of tuition, the monthly cost of rent, and the monthly cost of food as input from a user. Many students take out loans for college. In fact, student debt has surpassed credit card debt in the United States. We can implement a feature to read in an interest rate and the number of years expected to pay off the loan.
After taking all this data as input, we want to calculate the yearly cost of such an education, the four year cost, the monthly loan payment, and the total cost of the loan over time. Furthermore, we want to output this information on the command line in an attractive way, customized with the user’s name. Below is a sample execution of this program.
Welcome to the College Cost Calculator! Enter your first name: Holden Enter your last name: Caulfield Enter tuition per semester: $17415 Enter rent per month: $350 Enter food cost per month: $400 Annual interest rate: .0937 Years to pay back your loan: 10 College costs for Holden Caulfield *************************************** Yearly cost: $43830.00 Four year cost: $175320.00 Monthly loan payment: $2256.14 Total loan cost: $270736.5
Samples from a command line interface can be confusing because it’s difficult to see what’s output and what’s input. In this case, we have marked the input in bold so that it’s clear what the user enters. In this program, the names, the tuition, the rent, the food, the interest rate, and the years to pay back the loan are taken as input. Note that the dollar signs are not part of the input and are printed as a cue to the user and to give visual polish.
We hope you already have a good understanding of this problem, but there are a few mathematical details worth addressing. First, the yearly cost is twice the semester tuition plus 12 times the rent and food costs. The four year cost is simply four times the yearly cost. The monthly loan payment amount, however, requires a formula from financial mathematics. Let P be the amount of the loan (the principal). Let J be the monthly interest rate (the annual interest rate divided by 12). Let N be the number of months to pay back the loan (years of the loan times 12). Let M be the monthly payment we want to calculate, given by the following formula.

If you use the concepts and syntax from the previous chapter carefully, you might be able to solve this problem without reading further. However, there’s a depth to the ideas of types and operations that we haven’t explored fully. Getting a program to work is not enough. Programmers must understand every detail and quirk of their tools to avoid potential bugs.
3.2. Concepts: Types
Every operation inside of a Java program manipulates data. Often, this data is stored in variables, which look similar to variables from mathematics.
Consider the mathematical equation x + 3 = 7. In it, x has the value 4, and it always will. You can set up another equation in which x has a different value, but it won’t change in this one. Java variables are different. They’re locations where you can store something. If you decide later that you want to change what you stored there, you can put something else into the same location, overwriting the old value.
In contrast to a variable is a literal. A literal is a concrete value
that does not change, though it can be stored in a variable. Numbers
like 4 or 2.71828183 are literals. We need to represent text and
single characters in Java as well, and there are literals like
"grapefruit segment" and 'X' that fill these roles.
In Java, both variables and literals have types. If you think of a
variable as a box where you can hold something, its type is the shape of
that box. The kinds of literals that can be stored in that box must have
a matching shape. In the last chapter, we introduced the type int to
store integer values and the type double to store floating-point
values. Java is a strongly typed language, meaning that, if we declare
a variable of type int, we can only put int values into it (with a
few exceptions).
This idea of a type takes some getting used to. From a mathematical
perspective 3 and 3.0 are identical.
However, if you have an int variable in Java, you can store 3 into
it, but you can’t store 3.0. The type of a value will never change,
but you can convert a value from one type to an equivalent value in another type.
3.2.1. Types as sets and operations
Before we go any further, let’s look deeper at what a type really is. We
can think of a type as a set of elements. For example, int represents
a set of integer values (specifically, the integers between
-2,147,483,648 and 2,147,483,647, inclusive). Consider
the following declarations:
int x;
int y;These declarations indicate that the variables named x and y can
only contain integer values in the int range. Furthermore, a type only
allows specific operations. In Java, the int type allows addition,
subtraction, multiplication, division, and several other operations we’ll
talk about in Section 3.3, but there’s no built-in operation
to raise an int value to a power in Java. Let’s assume that x
has type int. As we discussed in the previous chapter, the
expression x + 2 performs addition between the variable represented by
x and the literal 2. Some languages use the operator ^ to mean
raising a number to a power. Following this notation, some beginning
Java programmers are tempted to write x ^ 2 to compute x squared.
The ^ operator does have a meaning in Java, but it doesn’t raise
values to a power. Other combinations of operators are simply illegal,
such as x # 2.
The idea of using types this way gives structure to a program. All
operations are well-defined. For example, you know that adding two int
values together will give you another int value. Java is a
statically typed language. This means that it can analyze all the types you’re
using in your program at compile-time and warn you if you’re doing
something illegal. Consequently, you’ll get a lot of compiler warnings
and errors, but you can be more confident that your program is correct
if all the types make sense.
3.2.2. Primitive and reference types in Java
As shown in Figure 3.1(a), there are two kinds of
types in Java: primitive types and reference types. Primitive types
are like boxes that hold single, concrete values. The primitive types in
Java are byte, short, int, long, float, double, boolean,
and char. These are types provided by the designers of Java, and it’s
not possible to create new ones. Each primitive type has a set of
operators that are legal for it. For example, all the numerical types
can be used with + and -. We’ll talk about these types and their
operators in great detail in Section 3.3.

int primitive type (b), the boolean primitive type (c), the String reference type (d), and a possible Aircraft reference type (e) are represented as sets of items with operations.Reference types work differently from primitive types. For one thing, a reference variable points at an object. This means that when you assign one reference variable to another, you aren’t getting a whole new copy of the object. Instead, you’re getting another arrow that points at the same object. The result is that performing an operation on one reference can effectively change another reference, if they’re both pointing at the same object.
Another difference is that reference variables (or simply references)
do not have a large set of operators that work on them. Every variable
can be used with the assignment (=) and the comparison (==)
operators. Every variable can also be concatenated with a String by
using the ` operator, but even if two objects represent numerical
values, they can't be added together with the ` operator.
References should still be thought of as types defining a set of objects
and operations that can be done with them. Instead of using operators,
however, references use methods. You’ve seen methods such as
System.out.print() and JOptionPane.showInputDialog() in the previous
chapter. A method generally has a dot (.) before it and always has
parentheses afterward. These parentheses contain the input parameters
or arguments that you give to a method. Using operators on primitive
types is convenient, but on the other hand, there is no limit to the
number, kind, or complexity of methods that can be used on references.
Another important feature of reference types is that anyone can define
them. So far, you’ve seen the reference types String and
JOptionPane. As we’ll discuss later, String is an unusual
reference type in that it is built deeply into the language. There are a
few other types like this (such as Object), but most reference types
could have been written by anyone, even you.
To create a new type, you write a class and define data and methods
inside of it. If you wanted to define a type to hold airplanes, you
might create the Airplane class and give it methods such as
takeOff(), fly(), and land() because those are operations that any
airplane should be able to do.
Once a class has been defined, it’s possible to instantiate an
object. An object is a specific instance of the type. For example, the
type might be Airplane, but the object might be referenced by a
variable called sr71Blackbird. Presumably, this object has a weight, a
maximum speed, and other characteristics that mark it as a Lockheed
SR-71 “Blackbird,” the famous spy plane. To summarize: An object is a
concrete instance of data. A reference is a variable that gives
a name to (points to) an object. A type is a class that both the
variable and the object have that defines what kinds of data the
object contains and what operations it can perform.
The following table lists some of the differences between primitive types and reference types.
| Primitive Types | Reference Types |
|---|---|
Created by the designers of Java |
Created by any Java programmer |
Use operators to perform operations |
Use methods to perform operations |
There are only eight different primitive types |
The number of reference types is unlimited and grows every time someone creates a new class |
Hold a specific numbers of bytes of data depending on the type |
The referenced object can hold arbitrary amounts of data |
Assignment copies a value from one place to another |
Assignment copies an arrow that points at an object |
Declaration creates a box to hold values |
Declaration creates an arrow that can point at an object, but only instantiation creates a new object |
3.2.3. Type safety
Why do we have types? There are weakly typed languages where you can store any value into almost any variable. Why bother with all these complicated rules? Most assembly languages have no notion of types and allow the programmer to manipulate memory directly.
Because Java is strongly typed, the type of every variable, whether primitive or reference, must be declared prior to its use. This constraint allows the Java compiler to perform many safety and sanity checks during compilation, and the JVM performs a few more during execution. These checks avoid errors during program execution that might otherwise be hard to find, errors that could lead to catastrophic failures of the program.
The Ariane 5 rocket is an example of a catastrophic failure due to a type error. On its first flight, the rocket left its flight path and eventually exploded. The failure was caused because of errors from converting a 64-bit floating-point to 16-bit signed integer value. The converted value was larger than the integer could hold, resulting in a meaningless value.
Converting from one type to another is called casting. The Ariane 5 failure was due to a problem with casting that was not caught. Even in Java, it’s possible for a human being to circumvent type safety with irresponsible casting.
3.3. Syntax: Types in Java
In this section we dig deeper into the type system in Java,
starting with variables and moving on to the properties of the eight
primitive types and the properties of String and other reference
types.
3.3.1. Variables and literals
To use a variable in Java, you must first declare it, which sets aside
memory to hold the variable and attaches a name to that space.
Declarations always follows the same pattern. The type is written first
followed by the identifier, or name, for the variable. Below we declare
a variable named value of type int.
int value;Note how we use the same pattern to declare a reference variable named
creature of type Wombat.
Wombat creature;You’re free to declare a variable and then end the line with a
semicolon (;), but it’s common to initialize a variable at the same
time. The following line simultaneously declares value and initializes
it to 5.
int value = 5;|
Pitfall: Multiple declarations
Don’t forget that you’re both declaring and initializing in a line like the above. Beginning Java programmers sometimes try to declare a variable more than once, as in the following: Java won’t allow two variables with the same name to exist in the
same block of code. The programmer probably intended the following,
which reuses variable This error is more common when several other lines of code lie between the two assignments. |
In some of the examples above, we’ve stored the value 5 into our
variable value. The symbol 5 is an example of a literal. A literal
is a value represented directly in code. It cannot be changed, but it
can be stored into variables that have a matching type. The values stored
into variables come from literals, input, or more complicated
expressions. Just like variables, literals have types. The type of 5
is int while the type of 5.0 is double. Other types have literals
written in ways we’ll discuss below.
3.3.2. Primitive types
The building blocks of all Java programs are primitive types. All objects must fundamentally contain primitive types deep down inside. There are eight primitive types. Half of them are used to represent integer values, and we’ll start by looking at those.
Integers: byte, short, int, and long
A variable intended to hold integer values can be declared with any of
the four types byte, short, int, or long. All of them are signed
(holding positive and negative numbers) and represent numbers in two’s
complement. They only differ by the range of values that each type can
hold. These ranges and the number of bytes used to represent variables
from each type are given below.
| Type | Bytes | Range | ||
|---|---|---|---|---|
byte |
1 |
-128 |
to |
127 |
short |
2 |
-32,768 |
to |
32,767 |
int |
4 |
-2,147,483,648 |
to |
2,147,483,647 |
long |
8 |
-9,223,372,036,854,775,808 |
to |
9,223,372,036,854,775,807 |
Note that the entire range of byte is included in that of short, of short
in that of int, and so on. We say that short is broader than
byte, int is broader than short, and long is broader than int.
A variable declared with type byte can only represent 256 different
values, the integers in the range -128 to 127. Why use byte at all,
then? Since a byte value only takes up a single byte, it can save
memory, especially if you have a list of variables called an array,
which we will discuss in Chapter 6. However, too narrow
of a range will result in underflow and overflow. Java programmers are
advised to stick with int for general use. If you need to represents
values larger than 2 billion or smaller than -2 billion, use long.
Once you’re an experienced programmer, you may occasionally use byte
and short to save space, but they should be used sparingly and for a
clear purpose.
Consider the following declarations.
byte age;
int numberOfRooms;
long foreverCounter = 0;The first of these statements declares age to be a variable of type
byte. This declaration means that age can assume any value from the
range for byte. For a human being, this limitation is reasonable (but
dangerously close to the limit) since there is no documented case of a
person living more than 122 years. Similarly, the next declaration
declares numberOfRooms to be of type int. The last declaration
declares foreverCounter to be of type long and initializes it to
0.
Since age is a variable, its value can change during program
execution. Note that the above declaration of age does not assign a
value to it. When they are declared, all integer variables are set to
0 by Java. However, to make sure that the programmer is explicit about
what he or she wants, the compiler will give an error in most cases if a
variable is used without first having its value set.
Like any other integer variable, we can assign age a value as follows.
age = 32;Doing so assigns the value 32 to variable age. Note that the Java
compiler would not complain if you were to assign -10 to the variable
age, even though it’s impossible for a human to have a negative age
(at least, without a time machine). Java attaches no meaning to the name
you give to a variable.
Earlier, we said that variables had to match the type of literals you
want to store into them. In the example above, we declared age with
type byte and then stored 32 into it. What is the type of 32? Is
it byte, short, int, or long? By default, all integer literals
have type int, but they can be used with byte or short variables
provided that they fit within the range. Thus, the following line causes
an error.
byte fingers = 128;If you want to specify a literal to have type long, you can append l
or L to it. Thus, 42 is an int literal, but 42L is a long
literal. You should always use the capital L since l can be difficult to
distinguish from 1.
At the time of this writing, Java 11 is the newest version of Java, but
Java 8 is most commonly used. In Java 7 and higher, you’re allowed
to put any number of underscores (_) inside of numerical literals to
break them up for the sake of readability. Thus, 123_45_6789 might
represent a social security number, or you could use underscores instead
of commas to write three million as 3_000_000. Since most compilers support
Java 7 or higher now, it’s reasonable to use this underscore notation in your
literals. Note that you should never use a comma in a numerical Java literal,
no matter which version of Java you’re using.
Floating-point numbers: float and double
To represent numbers with fractional parts, Java provides two floating-point
types, double and float. Because of limits on floating-point
precision discussed in Chapter 1, Java cannot
represent all real or rational numbers, but these types provide good
approximations. If you have a variable that takes on floating-point
values such as 3.14, 1.707 × 1025,
9.8, or similar, it ought to be declared as a double or a
float.
Consider the following declarations.
float roomArea;
double avogadro = 6.02214179E23The first of the above two statements declares roomArea to be of type
float. Note that the declaration does not initialize roomArea to any
value. Similar to integer primitive types, an uninitialized floating-point
variable contains 0.0, but Java usually forces the programmer to
assign a value to a variable before using it. The second of the above
two statements declares avogadro to be a variable of type double and
initializes it to the well-known Avogadro constant
6.02214179 × 1023. Note the use of E to mean
“ten to the power of.” In Java, you could write
0.33 × 10-12 as 0.33E-12, or the number
-4.325 × 1018 as -4.325E18 (or even -4.325E+18
if you’d like to write the sign of the exponent explicitly).
Accuracy in number representation
As discussed in Chapter 1, integer types
within their specified ranges have exact representations. For
example, if you assign 19 to a variable of type int and then print
this value, you always get exactly 19. Floating-point numbers do not
have this guarantee of exact representation.
Try executing the following statements within a Java program.
double test = 0.0;
test += 0.1;
System.out.println(test);
test += 0.1;
System.out.println(test);
test += 0.1;
System.out.println(test);Since we’re adding 0.1 each time, one would expect to see outputs of
0.1, 0.2, and 0.3. The first two numbers print as expected, but
the third number prints out as 0.30000000000000004. It may seem
counterintuitive, but 0.1 is a repeating decimal in binary, meaning that
it cannot be represented exactly using the 64-bit IEEE floating-point
standard. The System.out.println() method hides this ugliness by
rounding the output past a certain level of precision, but by the third
addition, the number has drifted far enough away from 0.3 that an
unexpected number peeks out.
Variables of type float give you an accuracy of about 6 decimal digits
while those of type double give about 15 decimal digits. Does the
accuracy of floating-point number representation matter? The answer to
this question depends on your application. In some applications, 6-digit
accuracy may be adequate. However, when doing large-scale simulations,
such as computing the trajectory of a spacecraft on a mission to Mars,
15-digit accuracy might be a matter of life or death. In fact, even
double precision may not be enough. There is a special BigDecimal
class which can perform arbitrarily high precision calculations, but due
to its low speed and high complexity, it should only be used in those
rare situations when a programmer requires a much higher level of
precision than what double provides.
Java programmers are recommended to use double for general purpose
computing. The float type should only be used in special cases where
storage or speed are critical and accuracy is not. Because of its
greater accuracy, double is considered a broader type than float.
You can store float values in a double without losing precision, but
the reverse is not true.
All floating-point literals in Java have type double unless they have
an f or F appended on the end. Thus, 3.14 is a double literal,
but 3.14f is a float literal.
Floating-point output
Formatting output for floating-point numbers has an extra complication compared with integer output: How many digits after the decimal point should be displayed? If you’re representing money, it’s common to show exactly two digits after the decimal point. By default, all of the non-zero digits are shown.
Instead of using System.out.print(), you can use System.out.format()
to control formatting. When using System.out.format(), the first
argument to the method is a format string, a piece of text that gives
all the text you want to output as well as special format specifiers
that indicate where other data is to appear and how it should be
formatted. This method takes an additional argument for each format
specifier you use. The specifier %d is for integer values, the
specifier %f is for floating-point values (including both float and
double types), and the specifier %s is for text. Consider the
following example:
System.out.format("%s! I broke %d records in %f seconds.\n", "Bob", 3, 2.4985);The output of this code is
Bob! I broke 3 records in 2.4985 seconds.
This kind of output is based on the printf() function used for output
in the C programming language. It allows the programmer to have a
holistic picture of what the final output might look like, but it also
gives control of formatting through the format specifiers. For example,
you can choose the number of digits for a floating-point value to
display after the decimal point by putting a . and the number between
the % and the f.
System.out.format("$%.2f\n", 123.456789 );The output of this code is:
$123.46
Note that the last visible digit is rounded instead of truncated. Note that %n is a special
format specifier that indicates a newline. To learn about other ways to use
format strings to manipulate output, read the Oracle
Formatter documentation.
Basic arithmetic
The following table lists the arithmetic operators available in Java. All of these operators can be used on both the integer primitive types and the floating-point primitive types.
| Operator | Meaning |
|---|---|
+ |
Add |
- |
Subtract |
* |
Multiply |
/ |
Divide |
% |
Modulus (remainder) |
The first four of these should be familiar. Addition, subtraction, and multiplication work as you would expect, provided that the result is within the range defined for the types you’re using, but division is a little confusing. If you divide two integer values in Java, you’ll get an integer as a result. If there would have been a fractional part, it will be truncated, not rounded. Consider the following.
int x = 1999/1000;In normal mathematics, 1,999 ÷ 1,000 = 1.999. In Java,
1999/1000 yields 1, and that’s what is stored in x. For
floating-point numbers, Java works much more like normal mathematics.
double y = 1999.0/1000.0;In this case, y contains 1.999. The literals 1999.0 and 1000.0
have type double. The type of y does not affect the division, but it
had to be double to be a legal place to store the result.
|
Pitfall: Unexpected integer division
It’s easy to focus on the variable and forget about the types involved in the operation. Consider the following. Because The code looks fine at first, but |
You may not have thought about this idea since elementary school, but
the division operator (/) finds the quotient of two numbers. The
modulus operator (%) finds the remainder. For example, 15 / 6 is
2 while 15 % 6 is 3 because 6 goes into 15 twice with 3 left
over. The modulus operator is usually used with integer values, but it’s
also defined to work with floating-point values in Java. It’s easy to
dismiss the modulus operator because we don’t often use it in daily
life, but it’s incredibly useful in programming. On its face, it allows
us to see the remainder after division. This idea can be applied to see
if a number is even or odd. It can also be used to compress a large
range of random integers to a smaller range or perform a kind of circular
arithmetic useful for cryptography. Keep an eye out for it.
We’ll use it many times in this book.
Precedence
Although all the previous examples use only one mathematical operator, you can combine several operators and operands into a larger expression like the following.
((a + b) * (c + d)) % eSuch expressions are evaluated from left to right, using the standard
order of operations: The * and / (and also %) operators are given
precedence over the + and - operators. Like in mathematics,
parentheses have the highest precedence and can be used to add clarity.
Thus, the order of evaluation of a + b / c is the same as
a + (b / c) but different from (a + b) / c.
Consider the following lines of code.
int a = 31;
int b = 16;
int c = 1;
int d = 2;
a = b + c * d - a / b / d;What’s the result? The first operation to be evaluated is c * d,
yielding 2. The next is a / b, yielding 1, which is then divided
by d, yielding 0. Next, b + 2 gives 18, and 18 - 0 is still
18. Thus, the value stored in a is 18.
Your inner mathematician might be nervous that a is used in the
expression on the right side of the assignment and is also the variable
where the result is stored, but this situation is very common in
programming. The value of a doesn’t change until after all the math
has been done. The assignment always happens last.
All of the operators we’ve discussed so far are binary operators.
This use of the word “binary” has nothing to do with base 2. A binary
operator takes two things and does something, like adding them together.
A unary operator takes a single operand and does something. The -
operator can be used as a unary operator to negate a literal, variable,
or expression. A unary negation has a higher precedence than the other
operators, just like in mathematics. In other words, the variable or
expression will be negated before it’s multiplied or divided. The +
operator can be used anywhere you’d use a unary negation, although
it doesn’t actually do anything. Consider the following statements.
int a = - 4;
int b = -c + d / -(e * f);
int s = +t + (-r);Shortcuts
Some operations happen frequently in Java. For example, increasing a
variable by some amount is a common task. If you want to increase the
contents of variable value by 10, you can write the following.
value = value + 10;Although the statement above is not excessively long, increasing a
variable is common enough that there’s shorthand for it. To achieve the
same effect, you can use the += operator.
value += 10;The += operator gets the contents of the variable, in this case value,
adds whatever is on its right side, in this case 10, and stores the
result back into the variable. Essentially, it saves you from writing
the name of the variable twice. And += is not the only shortcut. It’s
only one member of a family of shortcut operators that perform a binary
operation between the variable on the left side and the expression on
the right side and then store the value back into the variable. There’s
a -= operator that decreases a variable, a *= operator that scales a
variable, and several others, including shortcuts for bitwise operations
we cover in the next subsection.
| Operator | Example | Meaning |
|---|---|---|
+= |
a += b; |
a = a + b; |
-= |
a -= b; |
a = a - b; |
*= |
a *= b; |
a = a * b; |
/= |
a /= b; |
a = a / b; |
%= |
a %= b; |
a = a % b; |
&= |
a &= b; |
a = a & b; |
^= |
a ^= b; |
a = a ^ b; |
|= |
a |= b; |
a = a | b; |
<<= |
a <<= b; |
a = a << b; |
>>= |
a >>= b; |
a = a >> b; |
>>>= |
a >>>= b; |
a = a >>> b; |
These assignment shortcuts are useful and can make a line shorter and easier to read.
|
Pitfall: Weak type checking with assignment shortcuts
Because you can lose precision, it’s not allowed to store a In this case, the check makes a lot of sense. If you could add
This kind of error can cause problems when the program expects the value
of |
There are also two unary shortcuts. Incrementing a value by one and
decrementing a value by one are such common operations that they get
their own special operators, ++ and --.
| Operator | Example | Meaning |
|---|---|---|
++ |
a++; |
a = a + 1; |
-- |
a--; |
a = a - 1; |
Using either an increment or decrement changes the value of a variable.
In all other cases, the use of an assignment operator is required to
change a variable. Even in the binary shortcuts given before, the
programmer is reminded that an assignment is occurring because the =
symbol is present.
Both the increment and decrement operators come in prefix and postfix
flavors. You can write the ++ (or the --) in front of the variable
you’re changing or behind it.
int value = 5;
value++; // Now value is 6
++value; // Now value is 7
value--; // value is 6 againWhen used in a line by itself, either flavor works exactly the same. However, the incremented (or decremented) variable can also be used as part of a larger expression. In a larger expression, the prefix form increments (or decrements) the variable before the value is used in the expression. Conversely, the postfix form gives back a copy of the original value, effectively incrementing (or decrementing) the variable after the value is used in the expression. Consider the following example.
int prefix = 7;
int prefixResult = 5 + ++prefix;
int postfix = 7;
int postfixResult = 5 + postfix++;After the code is executed, the values of prefix and postfix are
both 8. However, prefixResult is 13 while postfixResult is only
12. The original value of postfix, which is 7, is added to 5,
and then the increment operation happens afterward.
|
Pitfall: Increment confusion
Incrementing a variable in Java is a very common operation. Expressions
like When confused, a programmer might write something like the following. At first glance, it may appear that the second line of code really means
|
In general it’s unwise to perform increment or decrement operations in the middle of larger expressions, and we advise against doing so. In some cases, code can be shortened by cleverly hiding an increment in the middle of some other expression. However, when reading back over the code, it always takes a moment to be sure that increment or decrement is doing exactly what it should. The additional confusion caused by this cleverness is not worth the line of code saved. Furthermore, the compiler will translate the operations into exactly the same bytecode, meaning that the shorter version is no more efficient than the longer version when executed.
Nevertheless, many programmers enjoy squeezing their code down to the smallest number of lines of code possible. You may have to read code that uses increments and decrements in clever (if obscure) ways, but you should always strive to make your own code as readable as possible.
Bitwise operators
In addition to normal mathematical operators, Java provides a set of
bitwise operators corresponding to the operations we discussed in
Chapter 1. These operators perform bitwise
operations on integer values. The bitwise operators are &, |, ^,
and ~ (which is unary). In addition, there are bitwise shift
operators: << for signed left shift, >> for signed right shift, and
>>> for unsigned right shift. There is no unsigned left shift operator
in Java.
| Operator | Name | Description |
|---|---|---|
& |
Bitwise AND |
Combines two binary representations into a new representation which has a 1 in every position where both the original representations have a 1 |
| |
Bitwise OR |
Combines two binary representations into a new representation which has a 1 in every position where either of the original representations has a 1 |
^ |
Bitwise XOR |
Combines two binary representations into a new representation which has a 1 in every position that the original representations have different values |
~ |
Bitwise NOT |
Takes a representation and creates a new representation in which every bit is flipped from 0 to 1 and 1 to 0 |
<< |
Signed left shift |
Moves all the bits the specified number of positions to the left, shifting 0s into the rightmost bits |
>> |
Signed right shift |
Moves all the bits the specified number of positions to the right, padding the left with copies of the sign bit |
>>> |
Unsigned right shift |
Moves all the bits the specified number of positions to the right, padding with 0s |
When used with byte and short, all bitwise operators will
automatically convert their operands to 32-bit int values. It’s
crucial to remember this conversion since the number of bits used for
representation is a fundamental part of bitwise operators.
The following example shows these operators in use. In order to understand the output, you need to understand how integers are represented in the binary number system, which is discussed in Section 1.3.
The following code shows a sequence of bitwise operations performed with
the values 3 and -7. To understand the results, remember that, in
32-bit two’s complement representation, 3 =
0000 0000 0000 0000 0000 0000 0000 0011 and -7 =
1111 1111 1111 1111 1111 1111 1111 1001.
int x = 3;
int y = -7;
int z = x & y;
System.out.println("x & y\t= " + z);
z = x | y;
System.out.println("x | y\t= " + z);
z = x ^ y;
System.out.println("x ^ y\t= " + z);
z = x << 2;
System.out.println("x << 2\t= " + z);
z = y >> 2;
System.out.println("y >> 2\t= " + z);
z = y >>> 2;
System.out.println("y >>> 2\t= " + z);The output of this fragment of code is:
x & y = 1 x | y = -5 x ^ y = -6 x << 2 = 12 y >> 2 = -2 y >>> 2 = 1073741822
Note how the escape sequence \t is used to put a tab character in the
output, making the results line up.
Why use the bitwise operators at all? Sometimes you may read data as
individual byte values, and you might need to combine four of these
values into a single int value. Although the signed left shift (<<)
and signed right shift (>>) are, respectively, equivalent to repeated
multiplications by 2 or repeated divisions by 2, they’re faster than
doing these operations over and over. Finally, some of these operations
are used for cryptographic or random number generation purposes.
Casting
Sometimes you need to use different types (like integers and floating-point
values) together. Other times, you have a value in one type but
need to store it in another (like when you’re rounding a double
to the nearest int). Some combinations of operators and types are
allowed, but others cause compiler errors.
The guiding rule is that Java allows an assignment from one type to another, provided that no precision is lost. That is, we can copy a value of one type into a variable of another type, provided that the destination variable has a broader type than the source value. The next few examples illustrate how to convert between different numerical types.
Consider the following statements.
short x = 341;
int y = x;Because the type of y is int, which is broader than short, it i’s legal
to assign the value in x to variable y. In
the assignment, a value with the narrower type short is converted to
an equivalent value with the broader type int. Converting from a
narrower type to a broader type is called an upcast or a promotion,
and Java allows it with no complaint. Most languages allow upcasts
without any special syntax because it’s always safe to move from a
narrower, more restrictive type to a broader, less restrictive one.
Consider these statements that declare variables a, b, and c and
compute a value for c.
int a = 10;
int b = 2;
byte c;
c = a + b;If you try compiling these statements as part of a Java program, you get an error message like the following.
Error: possible loss of precision found: int required: byte
The compiler generates the error above because the sum of two int
values is another int value, which could be greater than the maximum
value you can store in the byte variable c. In this example, you know
that the value 12 doesn’t exceed the maximum of 127, but the
Java compiler is inherently cautious. It complains whenever the type of
the expression to be evaluated is broader than the type of the
destination variable.
Integers are automatically converted to floating-point when needed. Consider the following statement.
double tolerance = 3;The literal 3 has type int, but it’s automatically converted to the
floating-point value 3.0 with type double. Again, double (and also
float) are considered broader types than any integer types.
Consequently, this type conversion is an upcast and is completely legal.
Upcasts also occur with arithmetic operations. Whenever you try to do arithmetic with two different numerical types, the narrower type is automatically upcast to the broader one.
double value = 3 + 7.2;In this statement, 3 is automatically upcast to its double version
3.0 because 7.2 has the broader double type.
In order to perform a downcast, the programmer has to mark that he or
she intends for the conversion to happen. A downcast is marked by
putting the result type in parentheses before the expression you want
converted. The next example illustrates how to cast a double value to
type int.
double to intThe following statements cause a compiler error because an expression
with type double cannot be stored into a variable with type int.
double roomArea = 3.5;
int houseArea = roomArea * 4.0;A downcast can lose precision, and that’s why Java doesn’t allow it.
Since a downcast is sometimes necessary, you can override Java’s type
system with an explicit cast. To do so, we put the expected (or desired)
result type in parentheses before the expression. In this case and many
others, it’s also necessary to surround the expression with
parentheses so that the entire expression (and not just roomArea) is
converted to type int.
double roomArea = 3.5;
int houseArea = (int) (roomArea * 4.0);In this case, the expression has value 14.0. Consequently, the int
version is 14. In general, the value could have a fractional part.
When casting from a floating-point type to an integer type, the
fractional part is truncated not rounded. Consider the following
statement:
int count = (int) 15.99999;Mathematically, it seems obvious that 15.99999 should be rounded to
the nearest int value of 16, but Java does not do this. Instead, the
code above stores 15 into count. If you want to round the value,
Java provides a method for rounding in the Math class. The rounding
(instead of truncating) version is given below.
int count = (int) Math.round(15.99999);The value given back by Math.round() has type long. The designers of
the Math class chose long so that the same method could be used to round
large double values into a long value, since the result might not
fit in an int value. Since long is a broader type than int, we
have to downcast the result to an int so that we can store it in
count.
double to floatConsider the following declaration and assignment of variable
roomArea.
float roomArea;
roomArea = 2.0;This assignment is illegal in Java, and the compiler gives an error message like the following.
Error: possible loss of precision found: double required: float
As we mentioned earlier, the literal 2.0 has type double. When you
try to assign a double value to a float variable, there’s always a
risk that precision will be lost. The best way to avoid the error above
is to declare roomArea with type double. Alternatively, we could
store the float literal 2.0f into roomArea. We could also assign
2 instead of 2.0 to roomArea, since the upcast from int is done
automatically.
Remember, you should almost always use the double type to represent
floating-point numbers. Only in rare cases when you need to save memory
should you use float values. By making it illegal to store 2.0 into
a float variable, Java’s encouraging you to use high precision
storage.
Numerical types and the conversions between them are critical elements of programming in Java, which has a strong mathematical foundation. In addition to these numerical types, Java also provides two other types that represent individual characters and Boolean values. We examine these next.
Characters: char
Sentences are made up of words. Words are made up of letters. Although
we have discussed powerful tools for representing numbers in Java,
we need a way to represent the letters and other characters we might
find in printed text. Values with the char type are used to represent
individual characters.
In the older languages of C and C++, the char type used 8 bits for
storage. From Chapter 1, you know that you can
represent up to 28 = 256 values with 8 bits. The Latin
alphabet, which is used to write English, uses 26 letters. If we need to
represent upper- and lowercase letters, the 10 decimal digits,
punctuation marks, and quite a few other special symbols, 256 values is
plenty. However, people all over the world use computers and want to
store text from their language written in their script digitally. Taking
the Chinese character system alone, some Chinese dictionaries list over
100,000 characters!
Java uses a standard called UTF-16 encoding to represent characters. UTF-16 is part of a larger international standard called Unicode, which is an attempt to represent most of the world’s writing systems as numbers that can be stored digitally. Most of the inner workings of Unicode aren’t important for day-to-day Java programming, but you can visit the Unicode site if you want more information.
In Java, each variable of type char uses 16 bits of storage.
Therefore, each character variable could assume any value from among a
total of 216 = 65,536 possibilities (although a few of
these are not legal characters). Here are a few declarations and
assignments of variables of type char.
char letter = 'A';
char punctuation = '?';
char digit = '7';We’re storing char literals into each of the variables above. Most of
the char literals you’ll use commonly are made by typing the single
character you want in single quotes ('), such a 'z'. These
characters can be upper- or lowercase letters, single numerical digits,
or other symbols.
The space character literal is ' ', but some characters are harder to
represent. For example, a new line (the equivalent of pressing
<enter>) is represented as a single character, but we can’t type a
single quote, hit <enter>, and then type the second quote. Instead,
the character to represent a new line is '\n', which we will refer to
simply as a newline. Every char variable can only hold a single
character. It appears that '\n' has multiple characters in it, but it
doesn’t. The use of the backslash (\) marks an escape sequence,
which is a combination of characters used to represent a specific
difficult to type or represent character. Here is a table of common
escape sequences.
| Escape Sequence | Character |
|---|---|
\n |
Newline |
\t |
Tab |
\' |
Single quote |
\\ |
Backslash |
Remember, everything inside of a computer is represented with numbers,
and each char value has some numerical equivalent. These numbers are
arbitrary but systematic. For example, the character 'a' has a
numerical value of 97, and 'b' has a numerical value of 98. The
codes for all of the lowercase Latin letters are sequential in
alphabetical order. (The codes for uppercase letters are sequential too,
but there’s a gap between them and the lowercase codes.)
Some Unicode characters are difficult to type because your keyboard or
operating system has no easy way to produce the character. Another kind
of escape sequence allows you to specify any character by its Unicode
value. There are large tables listing all possible Unicode characters by
numerical values. If you want to represent a specific literal, you type
'\uxxxx' where xxxx is a hexadecimal number representing the value.
For example, '\u0064' converted into decimal is
16 × 6 + 4 = 100, which is the letter 'd'.
If you print a char variable or literal directly, it prints the
character representation on the screen. For example, the following
statement prints A not 65, the Unicode value of 'A'.
System.out.println('A');However, the Unicode values are numbers. If you try to perform
arithmetic on them, Java will treat them like numbers. For example, the
following statement adds the integer equivalents of the characters
(65 + 66 = 131), concatenates the sum with the String
"C", and concatenates the result with a String representation of the
int literal 999. The surprising final output is 131C999.
System.out.println('A' + 'B' + "C" + 999);Booleans: boolean
If you’re new to programming, it may seem useless to have a type designed to hold only true and false values. These values are called Boolean values, and the logic used to manipulate them turns out to be crucial to almost every program. We use them to represent conditions in Chapter 4, Chapter 5, and beyond.
To store these truth values, Java uses the type boolean. There are
exactly two literals for type boolean: true and false. Here are
two declarations and assignments of boolean variables.
boolean awesome = true;
boolean testFailed = false;If we could only store these two literals, boolean variables would
have limited usefulness. However, Java provides a full range of
relational operators that allow us to compare values. Each of these
operators generates a boolean result. For example, we can test to see
if two numbers are equal, and the answer is either true or false.
All Java relational operators are listed in the table below. Assume that
all variables used in the Example column have a numeric type.
| Symbol | Read as | Example |
|---|---|---|
== |
equal to |
x + 3 == y * 2 |
!= |
not equal to |
x != y / 4 |
< |
less than |
x < 3.5 |
<= |
less than or equal to |
x <= y |
> |
greater than |
x > y+1 |
>= |
greater than or equal to |
x + y >= z |
The following declarations and assignments illustrate some uses of
boolean variables. Note the use of the relational operators == and
>.
int x = 3;
int y = 4;
boolean same = (x == 3);
same = (x == y);
boolean xIsGreater = (x > y);In the first use of == above, the value of same is true because
the value of x is 3. In the second comparison, the value of same
is false because the values of x and y are different. The value of
xIsGreater is also false since the value of x is not greater than
the value of y. All of the parentheses in this example are unnecessary
and are used only for clarity.
In addition to the relational operators, Java also provides logical
operators that can be used to combine or negate boolean values. These
are the logical AND (&&), logical OR (||), logical XOR (^), and
logical NOT (!) operators.
| Name | Operator | Description |
|---|---|---|
AND |
&& |
Returns |
OR |
|| |
Returns |
XOR |
^ |
Returns |
NOT |
! |
Returns the opposite of the value |
All of these operators, except for NOT, are binary operators. Logical
AND is used when you want your result to be true only if both the
operands being combined evaluate to true. Logical OR is used when you
want your result to be true if either operand is true. Logical XOR
is used when you want your result to be true if one but not both of
your operands is true. The unary logical NOT operator (!) results in
the opposite value of its operand, switching true to false or
false to true. Both the relational operators and the logical
operators are described in greater detail in
Chapter 4.
3.3.3. Reference types
Now we’ll move on to reference types, which vastly outnumber the primitive types, with new types created all the time. Nevertheless, the primitive types in Java are important, partly because they are the building blocks for reference types.
Recall that a variable with a reference type does not contain a concrete
value like a primitive variable. Instead, the value it holds is a
reference or arrow pointing to the “real” object. It’s like a name for
an object. When you declare a reference variable in Java, it doesn’t initially
point at anything, and you’ll get a compiler error if you try to use its value. For
example, the following code creates a Wombat variable called w, but it doesn’t
yet point at anything.
Wombat w;To create an object in Java, you use the new keyword followed by the
name of the type and parentheses, which can either be empty or contain
data you want to use to initialize the object. This process is called
invoking the constructor, which creates space for the object and then
initializes it with the values you specify or with default values if you
leave the parentheses empty. Below, we invoke the default Wombat
constructor and point the variable w at the resulting object.
w = new Wombat();Alternatively, a Wombat constructor might allow you to specify its mass in
kilograms when creating one, as follows.
w = new Wombat(26.3);Assignment of reference types points the two references to the same
object. Thus, we can have two different Wombat references pointing at
the same object.
Wombat w1 = new Wombat(26.3);
Wombat w2 = w1;
Wombat references pointing at the same object.Then, anything we do to w1 will affect w2 and vice versa. For
example, we can tell w1 to eat leaves using the eatLeaves() method.
w1.eatLeaves();Perhaps this will increase the mass of the object that w1 points at to
26.9 kilograms. But the mass of the object that w2 points at will be
increased as well, because they are the same object. Since primitive
variables hold values and not references to objects, this kind of code
works very differently with them. Consider the following.
int a = 10;
int b = a;
a = a + 5;In this code, a is initialized to have a value of 10, and b is
initialized to have whatever value a has, namely 10. The third line
increases the value of a to 15, but b remains at 10.

int variables store values, not references.Now that we’ve highlighted some of the differences between primitive and
reference types, we explain the String type more deeply. You use it
frequently, but it has a few unusual features that are not shared by
other reference types.
String basics
The String type is used to represent text in Java. A String object
contains a sequence of zero or more char values. Unlike every other
reference type, there is a literal form for String objects. These
literals are written with the text you want to represent inside of
double quotes ("), such as "Fight the power!". You can declare a
String reference and initialize it by setting it equal to another
String reference or a String literal. Like any other reference, you
could leave it uninitialized.
There’s a difference between an uninitialized String (a reference
that points to null) and a String of length 0. A String of length
0 is also known as an empty string and is written "". The space
character (' ') and escape sequences such as '\n' can also be parts of
a String and add to its length. For example, "ABC" contains three
characters, but the String "A B C" has five, because the spaces on
each side of 'B' count. The next example illustrates some ways of
defining and using the String type.
String assignmentThe following declarations define two String references named
greeting and title and initialize each with a literal.
String greeting = "Bonjour!"
String title = "French Greeting";As you’ve seen in Chapter 2,
we can output String values using System.out.print() and
JOptionPane methods.
System.out.println(greeting);
JOptionPane.showMessageDialog(null, greeting, title, JOptionPane.INFORMATION_MESSAGE);The first statement above displays Bonjour! on the terminal. The
second statement creates a dialog box with the title French Greeting
and the message Bonjour!
String operations
In Chapter 2, you saw that we
can concatenate two String objects into a third String object
using the + operator. This operator is unusual for a reference type.
Almost all other reference types are only able to use the assignment
operator (=) and the comparison operator (==). Like other reference
types, the String class provides methods for interaction. We introduce
a few String methods in this section and subsequent sections, but the
String class defines many more.
String concatenationHere’s another example of combining String objects using the +
operator.
String argument = "the cannon";
String phrase = "No argument but " + argument + "!";In these statements, we initialize argument to "the cannon". We then
compute the value of phrase by adding, or concatenating, three
String values: "No argument but ", the value of argument, and
"!". The result is "No argument but the cannon!". If argument had
been initialized to "a pie in the face", then phrase would instead point to
"No argument but a pie in the face!".
Another way of concatenating two String objects is by using the
String concat() method.
String argument = "the cannon";
String exclamation = "!";
String phraseStart = "No argument but ";
String phrase = phraseStart.concat(argument);
phrase = phrase.concat(exclamation);This sequence of statements gives the same result as the one above
using the ` operator. In practice, the `concat()` method is rarely
used because the ` operator is so convenient. Note that String
objects in Java are immutable, meaning that calling a method on a
String object will never change it. In the code above, calling
concat() creates new String objects. The phrase reference points
first at one String and then at a new String on the next line.
In this case the reference can be changed, but a String object
never changes once it’s been created. This distinction is a subtle but
important one.
A host of other methods can be used on a String just like concat().
For example, the length of a String can be found using the length()
method. The following statements prints 30 to the terminal.
String motto = "Fight for your right to party!";
System.out.println(motto.length()):String literals are String objects as well, and you can call methods
on them. The following code stores 11 into letters.
int letters = "cellar door".length();Remember that a String is a sequence of char values. If you want to
find out what char value sits at a particular location within a String, you
can use the charAt() method.
This method is called with an int value giving the index you want to
know about. Indexes inside of a String start at 0, not at 1.
Zero-based numbering is used extensively in programming, and we discuss
it further in Chapter 6. It may help if you think of
the index as the number of characters that appear before the character
at the specified index. The next example shows how charAt() can be
used.
char value at an indexTo see what char is at a given location, we call charAt() with the
index in question, as shown below.
String word = "antidisestablishmentarianism";
char letter = word.charAt(11);In this case, letter is assigned the value 'b'. Remember, indexes
for char values inside of a String start with 0. Thus, the char at
index 0 is 'a', the char at index 1 is 'n', the char at index 2
is 't', and so on. If you count up to the twelfth char (which has
index 11), it should be 'b'.
Every char inside of a String counts, whether it’s a letter, a
digit, a space, punctuation, or some other symbol.
String text = "^_^ l337 #haxor# skillz!";
System.out.println(text.charAt(10));This code prints out h since 'h' is the eleventh char (with index
10) in text.
A contiguous sequence of characters inside of a String is called a
substring. For example, a few substrings of
"Throw your hands in the air!" are "T", "Throw", "hands", and
"ur ha". Note that "Ty" is not a substring because these characters
don’t appear next to each other.
The next example shows how to use the substring() method to retrieve a
substring from an existing String.
You can generate a substring of a String (which is, itself, a String) using the
substring() method. The substring() method takes two arguments: the index where
the substring starts and the index just after it ends, as shown in the following code.
String description = "slovenly";
String emotion = description.substring(1,5);
System.out.println(emotion);This snippet of code prints love, since those are the characters at indexes
1 through 4 of "slovenly". Remember that String indexes are always zero-based. Also,
the second argument of substring() is the index after the last one you want in your substring.
Although this behavior is confusing, it’s a common design in many different string libraries in many
different languages. One way to think about it is that the length of the substring is the
second parameter minus the first. In this case, 5 - 1 = 4, the length of "love".
The String class also provides the indexOf() method to find the position
of a substring, as shown in the next example.
String searchSuppose we wish to find a String inside of another String. To do so,
we call the indexOf() method on the String we’re searching inside
of, with the String we’re searching for as the argument.
String countries = "USA Mexico China Canada";
String search = "China";
System.out.println(countries.indexOf(search));The indexOf() method returns an int value that gives the position of
the String we’re searching for. In the code above, the output is 11
because "China" appears starting at index 11 inside the countries
String. Another way to think about it is that there are 11 characters
before "China" in countries. If the given substring cannot be found, the indexOf()
method returns -1. For example, -1 will be printed to the terminal
if we replace the print statement above with the following.
System.out.println(countries.indexOf("Honduras"));There are several other methods provided by String that we introduce
as the need arises. If you are curious, you should look into the Java
documentation for String in the Oracle
String documentation for a
complete list of available methods.
3.3.4. Assignment and comparison
Both assigning one variable to another and testing two variables to see if they’re equal to each other are important operations in Java. These operations are used on both primitive and reference types, but there are subtle differences between the two that we discuss below.
Assignment statements
Assignment is the act of setting one variable to the value of another.
With a primitive type, the value held inside one variable is copied to
the other. With a reference type, the arrow that points at the object is
copied. All types in Java perform assignment with the assignment
operator (=).
As we’ve discussed, values can be computed and then assigned to variables as in the following statement.
int data = Integer.parseInt(response);In Java, a statement that computes a value and assigns it is called an assignment statement. The generic form of the assignment statement is as follows.
identifier = expression;Here, identifier gives the name of some variable. For example, in the
statement above, data is the name of the variable.
The right-hand side of an assignment statement is an expression that returns a value that’s assigned to the variable on the left-hand side. Even an assignment statement can be considered an expression, allowing us to stack multiple assignments into one line, as in the following code.
int a, b, c;
a = b = c = 15;The Java compiler checks for type compatibility between the left and the right sides of an assignment statement. If the right-hand side is a broader type than the left-hand side (or is completely mismatched), the compiler gives an error, as in the following cases.
int number = 4.9;
String text = 9;Comparison
Comparing two values to see if they’re the same uses the comparison
operator (==) in Java. With primitive types, this kind of check is
intuitive: The result is true if the two values are the same.
With reference types, the value held by the variable is the arrow
pointing to the object. Two reference variables could point to different
objects with identical contents and return false when compared to each
other. The following gives examples of these comparisons.
Consider the following lines of code.
int x = 5;
int y = 2 + 3;
boolean z = (x == y);The value of variable z is true because x and y contain the same
values. If x were assigned 6 instead, z would be false.
Now, consider the following code:
String thing1 = new String("Magical mystery");
String thing2 = new String("Magical mystery");
String thing3 = new String("Tragical tapestry");
thing1, thing2, and thing3 (a) in their initial states and (b) after the assignment thing1 = thing2;.This code declares and initializes three String values. Although it’s
possible to store String literals directly without invoking a String
constructor, we use this style of String creation to make our
point since Java can do some confusing optimizations otherwise.
Variables thing1 and thing2 point to String values that contain
identical sequences of characters. Variable thing3 points to a
different String. Consider the following statement.
boolean same = (thing1 == thing3);In this case the value of same is clearly false because the two
String values are not the same. What about the following case?
boolean same = (thing1 == thing2);Again, same contains false. Although, thing1 and thing2 point at
identical objects, they point at different identical objects. Since
the value held by a reference is the arrow that points to the object,
the comparison operator only shows that two references are the same if
they point at the same object.
To better understand comparison between reference types, consider Figure 3.4(a), which shows three different objects. Note that each reference points at a distinct object, even though two objects have the same contents.
Now consider the following assignment.
thing1 = thing2;As shown in Figure 3.4(b), this assignment points
reference thing1 to the same location as reference thing2. Then,
(thing1 == thing2) would be true.
The == operator is generally not very useful with references, and the
equals() method should be used instead. This method compares the
contents of objects in whatever way the designer of the type specifies.
For example:
thing1.equals(thing2)This statement is true when thing1 and thing2 are pointing at identical
String objects even if they’re different objects.
3.3.5. Constants
In addition to normal variables, we can define named constants. A
named constant is similar to a variable of the same type except that its
value cannot be changed once set. A constant in Java is declared like
any other variable with the addition of the keyword final before the
declaration.
The convention in Java (and many other languages) is to name constants
with all capital letters. Because camel case can no longer be used to
tell where one word starts and another ends, an underscore (_) is
used to separate words. Here are a few examples of named constant
declarations.
final int POPULATION = 25000;
final double PLANCK_CONSTANT = 6.626E-34;
final boolean FLAG = false;
final char FIRST_INITIAL = 'A';
final String MESSAGE = "All your base are belong to us.";In this code, the value of POPULATION is 25000 and cannot be
changed. For example, if you now write POPULATION = 30000; on a later
line, your compiler will give an error. PLANCK_CONSTANT, FLAG,
FIRST_INITIAL, and MESSAGE are also defined as named constants.
Because of the syntax Java uses, these constants are sometimes referred
to as final variables.
In the case of MESSAGE and all other reference variables, being
final means that the reference can never point at a different object.
Even with a final reference, the objects themselves can change if
their methods allow it. However, String objects can
never change since they’re immutable.
Named constants are useful in two ways. First, a well-named constant can
make your code more readable than using a literal. Second, if you do
need to change the value to a different constant, you only have to
change it in one place. For example, if you have used 25000 in five
different places in your program, changing it to 30000 requires five
changes. If you have used POPULATION throughout your program instead
of a literal, you only have to change its value once.
3.4. Syntax: Useful libraries
Computer software is difficult to write, but many of the same problems
come up over and over. If we had to solve these problems every time we
wrote a program, we’d never get anywhere. Java allows us to use code
other people have written called libraries. One selling point of Java
is its large standard library that can be used by any Java programmer
without special downloads. You’ve already used the Scanner class,
the Math class, and perhaps the JOptionPane class, which are all
part of libraries. Below, we’ll go deeper into the Math class and a
few other useful libraries.
3.4.1. The Math library
Basic arithmetic operators are useful, but Java also provides a rich set
of mathematical methods through the Math class.
The following table lists a few of the methods available. For a
complete list of methods provided by the Math class at the time of
writing, see the Oracle
Math documentation.
| Method | Sample use | Purpose |
|---|---|---|
Trigonometric functions |
||
cos() |
double adjacent = hypotenuse * Math.cos(theta); |
Find the cosine of the argument. |
sin() |
double opposite = hypotenuse * Math.sin(theta); |
Find the sine of the argument. |
tan() |
double opposite = adjacent * Math.tan(theta); |
Find the tangent of the argument. |
Exponentiation and logarithms |
||
exp() |
double population = 250 * Math.exp(0.03 * time); |
Compute ex, where x is the argument. |
log() |
double digits = Math.log(1000000); |
Compute the natural logarithm of the argument. |
pow() |
double money = principal * Math.pow(1.0 + rate, time); |
Compute ab, where a and b are the first and second arguments. |
Miscellaneous |
||
random() |
double percent = Math.random(); |
Generate a random number x where 0.0 ≤ x < 1.0. |
round() |
long items = Math.round(material); |
Round to the nearest |
sqrt() |
double hypotenuse = Math.sqrt(a*a+b*b); |
Compute the square root of the argument. |
Math library usageHere’s a program that uses the Math.pow() method to compute compound
interest. Unlike Scanner and JOptionPane, the Math class is
imported by default in Java programs and requires no explicit import
statement.
import java.util.*;
class CompoundInterestCalculator {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("Compound Interest Calculator");
System.out.println();
System.out.print("Enter starting balance: ");
double startingBalance = in.nextDouble();
System.out.print("Enter interest rate: ");
double rate = in.nextDouble();
System.out.print("Enter time in years: ");
double years = in.nextDouble();
System.out.print("Enter compounding frequency: ");
double frequency = in.nextDouble();
double newBalance = startingBalance *
Math.pow(1.0 + rate/frequency, frequency*years);
double interest = newBalance - startingBalance;
System.out.println("Interest earned: $" + interest);
System.out.println("New balance: $" + newBalance);
}
}In addition to methods, the Math library contains named constants
including Euler’s number e and π. These
are written in code as Math.E and Math.PI, respectively. For
example, the following assignment statement computes the circumference
of a circle with radius given by the variable radius, using the
formula 2πr.
double circumference = 2*Math.PI*radius;3.4.2. Random numbers
Random numbers are often needed in applications such as games and scientific simulations. For example, card games require a random distribution of cards. To simulate a deck of 52 cards, we could associate an integer from 1 to 52 with each card. If we had a list of these values, we could swap each value in the list with a value at a random location later in the list. Doing so is equivalent to shuffling the deck.
Java provides the Random class in package java.util to generate
random values. Before you can generate a random number with this class,
you need to create a Random object as follows.
Random random = new Random();Here we’ve created an object named random of type Random.
Depending on the kind of random value you need, you can use the
nextInt(), nextBoolean(), or nextDouble() to generate a random
value of the corresponding type.
// Random integer with all values possible
int balance = random.nextInt();
// Random integer between 0 (inclusive) and 130 (exclusive)
int humanAge = random.nextInt(130);
// Random boolean value
boolean gender = random.nextBoolean();
// Random floating-point value between 0.0 (inclusive) and 1.0 (exclusive)
double percent = random.nextDouble();In these examples, inclusive means that the number could be generated,
while exclusive means that the number cannot be. Thus, the call
random.nextInt(130) generates the integers 0 through 129 but never
130. Exclusive upper bounds on ranges of random values are very common
in programming.
To generate a random int between values a and b, not including
b, use the following code, assuming you have a Random object named
random.
int count = random.nextInt(b - a) + a;The nextInt() method call generates a value between 0
and b - a, and adding a shifts it into the
range from a up to (but not including) b.
Generating a random double between values a and b is similar
except that nextDouble() always generates a value between 0.0 and
1.0, not including 1.0. Thus, you must scale the output by b - a
as shown below.
double value = random.nextDouble()*(b - a) + a;The following example illustrates a potential use of random numbers in a video game.
Suppose you’re designing a video in which the hero must fight a dragon with random attributes. Program 3.2 generates random values for the age, height, gender, and hit points of the dragon.
import java.util.*; (1)
public class DragonAttributes {
public static void main(String[] args) {
Random random = new Random(); (2)
int age = random.nextInt(100) + 1; (3)
double height = random.nextDouble()*30; (4)
boolean gender = random.nextBoolean(); (5)
int hitPoints = random.nextInt(51) + 25; (6)
System.out.println("Dragon Statistics");
System.out.println("Age:\t\t" + age);
System.out.format("Height:\t\t%.1f feet\n", height);
System.out.println("Female:\t\t" + gender);
System.out.println("Hit points:\t" + hitPoints);
}
}| 1 | We begin by importing java.util.* to include all the classes
in the java.util package, including Random. |
| 2 | Then, we create an object random of type Random. |
| 3 | We use random to generate a random int between 0 and 99, to which we add 1, making an age between 1 and 100. |
| 4 | To generate the height, we multiply a random double by 75, yielding a value between 0.0 and 75.0 (exclusive). |
| 5 | Since there are only two choices for a dragon’s gender, we generate a
random boolean value, interpreting true as female and false as
male. |
| 6 | Finally, we determine the number of hit points the dragon has by
generating a random int between 0 and 50, then add 25 to it,
yielding a value between 25 and 75. |
Because we are using random values, the output of Program 3.2 changes every time we run the program. Sample output is given below.
Dragon Statistics Age: 90 Height: 13.7 feet Female: true Hit points: 67
If you only need a random double value, you can generate a number
between 0.0 and 1.0 (exclusive) using the Math.random() method
from the Math class. This method is a quick and dirty way to generate
random numbers without importing java.util.Random or creating a
Random object.
The random numbers generated by the Random class and by
Math.random() are pseudorandom numbers, meaning that they’re
generated by a mathematical formula instead of truly random events. Each
number is computed using the previous one, and the starting number is
determined using time information from the OS. For most purposes, these
pseudorandom numbers are good enough. Since each number can be predicted
from the previous one, pseudorandom numbers are insufficient for some
security applications. For those cases, Java provides the SecureRandom
class which is slower than Random but produces random numbers that
are much harder to predict.
3.4.3. Wrapper classes
Reference types have methods that allow a user to interact with them in
many useful ways. The primitive types (byte, short, int, long,
float, double, char, and boolean) do not have methods, but we
sometimes need to manipulate them with methods or store them in a place
that requires a reference type.
To deal with such situations, Java uses wrapper classes, reference
types that correspond to each primitive type. Following Java conventions
for class names, the wrapper types all start with an uppercase letter
but are otherwise similar to the name of the primitive type they
support: Byte, Short, Integer, Long, Float, Double,
Character, and Boolean.
String to numerical conversions
A common task for a wrapper class is to convert a String
representation of a number such as "37" or "2.097" to its
corresponding numeric value. We had such a situation in
Program 2.3, where we did the conversion as follows.
String response = JOptionPane.showInputDialog(null,
"Enter the height: ", title, JOptionPane.QUESTION_MESSAGE);
height = Double.parseDouble(response);This code uses the JOptionPane.showInputDialog() method to read from
the user the height at which a ball is dropped. This method always
returns data as a String. In order for us to do computation with the
value, we need to convert it to a numeric type, such as an int or a
double. To do so, we use the appropriate Byte.parseByte(),
Short.parseShort(), Integer.parseInt(), Long.parseLong(),
Float.parseFloat(), or Double.parseDouble() method.
The following example shows conversions from a String to a number
using three of these methods.
String to numeric conversionConsider the following statements that show how a string can be converted to a numerical value.
String text = "15";
int count = Integer.parseInt(text);
float value = Float.parseFloat(text);
double tolerance = Double.parseDouble(text);In this example, we declare a String object named text and
initialize it to "15". Since text is a String and not a number,
arithmetic expressions such as (text*29) are illegal.
To use the String "15" in a numerical computation, we need to
convert it to a number. We used the Integer.parseInt(),
Float.parseFloat(), and Double.parseDouble() methods to convert the
String to int, float, and double values, respectively. Each
method gives us 15 stored as the appropriate type.
What happens if the String "15.5" (or even "cinnamon") is given as
input to the Integer.parseInt() method? If the String is not
formatted as the appropriate kind of number, Java throws a
NumberFormatException, probably crashing the program. An exception
is an error or other unexpected situation that happens in the middle of
running a program. We discuss how to work with exceptions in Chapter 12.
Character methods
When working with char values, it can be useful to know whether a
particular value is a digit, a letter, or has a particular case. It may
also be useful to convert a char to upper- or lowercase. Here is a
partial list of the methods provided by the Character wrapper class to
do these tasks.
| Method | Purpose |
|---|---|
isDigit(char value) |
Returns |
isLetter(char value) |
Returns |
isLetterOrDigit(char value) |
Returns |
isLowerCase(char value) |
Returns |
isUpperCase(char value) |
Returns |
isWhitespace(char value) |
Returns |
toLowerCase(char value) |
Returns a lowercase version of |
toUpperCase(char value) |
Returns an uppercase version of |
For example, the variable test contains true after the following
code is executed.
boolean test = Character.isLetter('x');And the variable letter contains 'M' after the following code is
executed.
char letter = Character.toUpperCase('m');These methods can be especially useful when processing input.
Maximum and minimum values
As you recall from Chapter 1, integer arithmetic in Java has limitations. If you increase a large positive number past its maximum value, it becomes a large-magnitude negative number, a phenomenon called overflow. Conversely, if you decrease a large-magnitude negative number past its minimum value, it becomes a large positive number, a phenomenon called underflow.
With floating-point numbers, increasing their magnitudes past their maximum values results in special values that Java reserves to represent either positive or negative infinity, as the case may be. If a floating-point value gets too close to zero, it eventually rounds to zero.
In addition to useful conversion methods, the numerical wrapper classes
also have constants for the maximum and minimum values for each type.
Instead of trying to remember that the largest positive int value is
2,147,483,647, you can use the equivalent
Integer.MAX_VALUE.
The MAX_VALUE constants are always the largest positive number that
can be represented with the corresponding type. The MIN_VALUE is more
confusing. For integer types, it’s the largest magnitude negative
number. For floating-point types, it’s the smallest positive non-zero
value that can be represented. Here is a table listing these constants.
| Constant | Meaning |
|---|---|
Byte.MAX_VALUE |
Most positive value a |
Byte.MIN_VALUE |
Most negative value a |
Short.MAX_VALUE |
Most positive value a |
Short.MIN_VALUE |
Most negative value a |
Integer.MAX_VALUE |
Most positive value an |
Integer.MIN_VALUE |
Most negative value an |
Long.MAX_VALUE |
Most positive value a |
Long.MIN_VALUE |
Most negative value a |
Float.MAX_VALUE |
Largest absolute value a |
Float.MIN_VALUE |
Smallest absolute value a |
Double.MAX_VALUE |
Largest absolute value a |
Double.MIN_VALUE |
Smallest absolute value a |
The wrap-around nature of integer arithmetic means that adding 1 to
Integer.MAX_VALUE results in Integer.MIN_VALUE. Note that all
integer arithmetic in Java is done assuming type int, unless
explicitly specified otherwise. Thus, Short.MAX_VALUE + 1 does not
overflow to a negative value unless you store the result into a short.
The same rules apply to underflow.
Overflow and underflow do not work in the same way with the floating-point
numbers represented by float and double. The expression
Double.MAX_VALUE + 1 results in Double.MAX_VALUE because 1 is so
small in comparison that it’s lost in rounding error. However,
1.5*Double.MAX_VALUE results in Double.POSITIVE_INFINITY, a
constant used to represent any value larger than Double.MAX_VALUE.
Since Double.MIN_VALUE is the smallest non-zero number,
Double.MIN_VALUE - 1 evaluates to -1.0.
Using wrapper classes for storage
Wrapper classes in Java have a split personality. On the one hand, the classes themselves can be used for the utility methods and constants we described above. However, objects of these same wrapper classes can be used in an entirely separate way to store primitive values. Each primitive type can be stored in its wrapper type as shown below.
Integer fingers = new Integer(5);
Double pi = new Double(3.141592);
Character question = new Character('?');Why would we want to do this? There are many situations in which a library method or data structure requires a reference type, not a primitive type. These wrappers were designed for these cases when you have to treat a primitive type as an object.
Object value = new Integer(42);To make working with wrapper classes easier, Java 5 and higher support automatic boxing and unboxing, meaning that primitive types will automatically be converted to their wrapper types (and vice versa) when appropriate. Thus, the earlier code could be written as follows.
Integer fingers = 5;
Double pi = 3.141592;
Character question = '?';Programmers who don’t understand wrapper classes will sometimes use
primitive types and wrapper classes interchangeably, mixing double and
Double, for example. Avoid using wrapper classes unnecessarily, since
they require more memory and more computation to perform operations.
Fortunately, automatic boxing and unboxing reduce the need to think about wrapper classes, and most programmers will rarely need to declare an explicit wrapper reference. We’ll discuss wrapper classes further in Chapter 18, where they are used to allow generic classes to store primitive types as well as reference types.
3.5. Solution: College cost calculator
In this chapter, we introduced and more fully explained many aspects of manipulating data in Java, including declaring variables, assigning values, performing simple arithmetic and more advanced math, inputting and outputting data, and using the type system, which includes subtle differences between primitive and reference types. Our solution to the college cost calculator problem posed at the beginning of the chapter uses all of these features at some level. We present this solution below.
import java.util.*; (1)
public class CollegeCosts {
public static void main(String[] args) { (2)
System.out.println("Welcome to the College Cost Calculator!"); (3)
Scanner in = new Scanner(System.in); (4)| 1 | The first step in our solution is to
import java.util.* so that we can use the Scanner class. |
| 2 | After we start the enclosing CollegeCosts class, we begin the main() method. |
| 3 | We print a welcome message for the user. |
| 4 | Then, we create a Scanner object. |
Next is a sequence of prompts to the user interspersed with input done
with the Scanner object.
System.out.print("Enter your first name:\t\t");
String firstName = in.next(); (1)
System.out.print("Enter your last name:\t\t");
String lastName = in.next(); (2)
System.out.print("Enter tuition per semester:\t$");
double semesterTuition = in.nextDouble(); (3)
System.out.print("Enter rent per month:\t\t$");
double monthlyRent = in.nextDouble(); (4)
System.out.print("Enter food cost per month:\t$");
double monthlyFood = in.nextDouble(); (5)
System.out.print("Annual interest rate:\t\t");
double annualInterest = in.nextDouble(); (6)
System.out.print("Years to pay back your loan:\t");
int years = in.nextInt(); (7)| 1 | The program reads the user’s first name as a
String, |
| 2 | the user’s last name as a String, |
| 3 | the per-semester tuition cost as a double, |
| 4 | the monthly cost of rent as a double, |
| 5 | the monthly cost of food as a double, |
| 6 | the interest rate for the loan as a double, |
| 7 | and the number of years needed to pay back the loan as an
int. |
The next segment of code completes the computations needed.
double yearlyCost = semesterTuition * 2.0 + (monthlyRent + monthlyFood) * 12.0; (1)
double fourYearCost = yearlyCost * 4.0; (2)
double monthlyInterest = annualInterest / 12.0; (3)
double monthlyPayment = fourYearCost * monthlyInterest / (4)
(1.0 - Math.pow(1.0 + monthlyInterest, -years * 12.0));
double totalLoanCost = monthlyPayment * 12.0 * years; (5)| 1 | It finds the total yearly cost by doubling the semester cost, multiplying the monthly rent and food costs by 12, and summing the answers together. |
| 2 | The four year cost is simply four times the yearly cost. |
| 3 | To find the monthly payment, we find the monthly interest by dividing the annual interest rate by 12 and plugging this value into the formula from the beginning of the chapter. |
| 4 | Finally, the total cost of the loan is the monthly payment times 12 times the number of years. |
All that remains is to print out the output.
System.out.println("\nCollege costs for " + firstName + " " + lastName ); (1)
System.out.println("***************************************");
System.out.format("Yearly cost:\t\t\t$%.2f%n", yearlyCost); (2)
System.out.format("Four year cost:\t\t\t$%.2f%n", fourYearCost);
System.out.format("Monthly loan payment:\t\t$%.2f%n", monthlyPayment);
System.out.format("Total loan cost:\t\t$%.2f%n", totalLoanCost );
}
}| 1 | First, we output a header describing the following output as college costs for the user. |
| 2 | Using
System.out.format() as described in Section 3.3.2, we print out the yearly cost, four year cost, monthly loan
payment, and total cost, all formatted with dollar signs, two places after
the decimal point, and tabs so that the output lines up. |
3.6. Concurrency: Expressions
In Section 2.5, we introduced the ideas of task and domain decomposition that could be used to solve a problem in parallel. By splitting up the jobs to be done (as in task decomposition) or dividing a large amount of data into pieces (as in domain decomposition), we can attack a problem with several workers to finish the work more quickly.
3.6.1. Splitting expressions
Performing arithmetic is some of the only Java syntax we’ve introduced that can be used to solve problems directly, but evaluating a single mathematical expression usually does not warrant concurrency. If the terms in the expression are themselves complex functions (such as numerical integrations or simulations that produce answers), it might be reasonable to evaluate these functions concurrently.
In this section, we give an example of splitting an expression into smaller sub-expressions that could be evaluated concurrently. The basic steps underlying the concurrent evaluation of expressions are the following.
-
Identify sub-expressions that are independent of each other.
-
Create a separate thread to evaluate each sub-expression.
-
Combine the results from each thread to obtain a final answer.
While this sequence of steps looks simple, each step could be complex. Worse, being careless at any step could result in a concurrent solution that runs slower than the sequential solution or even gives the wrong answer. The following example illustrates these steps.
Consider the following statement:
double value = f(a,b)*g(c);This statement evaluates methods f() and g(), multiplies the
computed values, and assigns the result to variable value. In
Figure 3.5, we show two ways of evaluating the
expression f(a,b)*g(c). Figure 3.5(a) shows
sequential evaluation of the expression, where f() is computed, g()
follows, and then the two results are multiplied to get the final value.
Figure 3.5(b) shows evaluation of the expression
in which f() and g() are evaluated concurrently instead.

value = f(a,b)*g(c) with (a) sequential and (b) concurrent approaches.On a multicore processor, the computation of f() and g() could be
carried out on separate cores. We can create one thread for each method
and wait for the threads to complete. Upon completion, we can retrieve
the results of each computation and multiply them together as in
Figure 3.5(b). Program 3.3
illustrates this concurrent approach.
public class SplitExpression {
public static void main(String[] args) {
ComputeF fThread = new ComputeF(3.14, 2.99); (1)
ComputeG gThread = new ComputeG(5.55); (2)
fThread.start(); (3)
gThread.start(); (4)
try {
fThread.join(); (5)
gThread.join(); (6)
double fResult = fThread.getResult(); (7)
double gResult = gThread.getResult(); (8)
double answer = fResult*gResult; (9)
System.out.println("Result of f: " + fResult );
System.out.println("Result of g: " + gResult );
System.out.println("Final answer: " + answer);
}
catch(InterruptedException e){
System.out.println("Computation interrupted!");
}
}
}| 1 | We create an object named fThread which takes two arguments, 3.14 and 2.99 in this example. |
| 2 | We create another object named gThread that takes one, 5.55. Both of these objects have types that extend the Thread class, which means that they can be made to run independently. |
| 3 | We start the first thread running. |
| 4 | We start the second thread running. Every object whose type is Thread (or a child of Thread, which we will discuss in Chapter 11) has a start() method which begins its execution as a separate thread. |
| 5 | We wait for the first thread to finish. How do we know when a thread is done executing? Every Thread object has a join() method. If some code calls a thread’s join() method, the method will not return until the thread is finished. When code is waiting for a thread to finish, it’s possible for it to be interrupted if some other thread has gotten tired of the code waiting around doing nothing. If that happens, an InterruptedException is thrown. Exceptions are the way that Java deals with errors and other unusual situations. We’ll discuss them further in
Chapter 12, but for now, you only need to know that
code (like the join() method) that can cause certain kinds of
exceptions (like the InterruptedException) needs to be enclosed in a
try block. After the try block comes a catch block that says what
to do in the even of that exception. In our case, we print out
"Computation interrupted!" |
| 6 | We wait for the second thread to finish. |
| 7 | Once the threads have completed their respective tasks, the execution of
Program 3.3 resumes, and we obtain the result of the
computation done by fThread by calling its getResult() method. |
| 8 | On the next line, we call the getResult() method on gThread to obtain
its result. Note that we could have called these getResult() methods
before the join() calls, but the computations might not have
completed, yielding invalid or incorrect results (or crashing the
program). |
| 9 | Finally, these two computed values are multiplied to get the final result, which is assigned to answer and printed. |
We would like to show how classes ComputeF and ComputeG are written,
but we’ll hold off since they use concepts relating to methods, class
design, and inheritance that we’ll cover in Chapter 8, Chapter 9, and Chapter 11.
If you don’t understand all the elements of Program 3.3, don’t despair! We’re trying to give you an example of what concurrency looks like in Java, but you can’t be expected to master all the details at this stage. However, concurrency in Java will often follow the steps shown:
-
Creation of
Thread(or children ofThread) objects -
Calling the
start()method on these objects to start them executing -
Calling the
join()method on them to wait for them to finish -
Retrieving the results (if any) of the computations done by the objects
3.6.2. Care in splitting expressions
The above example illustrates how you could split an expression and
evaluate it concurrently. Note the following points when deciding
whether or not to use concurrency. First, your program will run faster
concurrently only if the work done is complex enough that its
computation takes significantly longer than the time to create the
necessary threads. In the example above, the methods f() and g()
must be complex enough that it takes a significant amount of time to
evaluate them. Otherwise, concurrency won’t reduce the running time.
This aspect of speedup is explained in detail in
Chapter 13.
Second, splitting an expression (or any complex sequence of
computations) is easy when its individual components are independent. If
they are interdependent, splitting requires care to avoid subtle programming
errors. Consider the expression f(a) + g(b) and suppose that
f() modifies the value of b during execution. Such a modification is
called a side effect. This side effect creates a dependency between
f() and g(). Concurrent execution of these two methods must be done
carefully, if it can be done at all. Chapter 14
discusses concurrency in the presence of dependencies.
3.7. Summary
In a strongly typed language such as Java, types are an important concept. Every literal and variable in Java has a type, which specifies the possible values items with that type could have and the operations that can be done with them. Types are used to catch programming errors at compile time.
Java has a small set of primitive types such as int and double
that hold single values and use operators to manipulate them. Java also
has reference types, which use primitive types as building blocks, can
be created by any Java programmer, can contain arbitrarily complex data,
and are manipulated with methods. One of the most commonly used
reference types is String, which is used to store text of any length.
A number of library classes have been provided by the developers of
Java. Programs performing mathematical operations beyond simple
arithmetic may need to use methods from the Math class. Programs that
need to generate random numbers can use methods from the Random class.
Conversions and other useful manipulations of primitive types are
provided by wrapper classes.
We also gave a taste of the syntax for creating, running, and waiting for the completion of threads. Such threads could be used to speed up the evaluation of computations on multicore processors, but only if the computations are long, complex, and not too interdependent.
3.8. Exercises
Conceptual Problems
-
What is the difference between the set of integers from mathematics and the sets defined by
intandlong? -
In Example 3.7, the sum of two
intvariables was anotherintvalue, which could not be stored into abytevariable. Would this code have worked if variablesaandbhad been declared with typebyte? What ifawas assigned121andbwas assigned98? -
The following three statements are legal Java (if properly included inside of a method). However, if we changed
2to2.0or5to5.0, the statements would not be legal. Explain why.float roomArea = 2; float homeArea = 5; float area = roomArea * homeArea; -
Consider the following variable declarations.
int x = 3, y = 4, z = -9; float p = 3.99f, q = -9.89f; int population1 = 15000, population2 = 8000; final double MAXIMUM_LEVEL = 350; double limitPerCapita = 0.03; int age = 14; final int MAXIMUM_AGE = 23; boolean allowed = false;Now evaluate each of the following expressions to
trueorfalse.-
MAXIMUM_LEVEL/population1 > limitPerCapita && MAXIMUM_LEVEL/population2 < limitPerCapita -
MAXIMUM_LEVEL/population1 > limitPerCapita || MAXIMUM_LEVEL/population2 < limitPerCapita -
age < MAXIMUM_AGE && allowed -
(x < y && y > z) || (p > q && population1 < population2)
-
-
Evaluate the following expressions by hand and then check the results with a Java compiler.
-
5 & 6 -
5 | 6 -
5 ^ 6 -
~5 -
5 >> 2 -
5 << 2 -
5 >>> 2
-
-
Evaluate the following expressions by hand and then check the results with a Java compiler.
-
Byte.MIN_VALUE - 1 -
Byte.MAX_VALUE + 1 -
Integer.MIN_VALUE - 1
-
-
Evaluate the following expressions by hand and then check the results with a Java compiler.
-
Float.MAX_VALUE + 1 -
Double.MAX_VALUE - 1 -
-Double.MAX_VALUE - 1 -
-Double.MIN_VALUE - 1 -
-Double.MIN_VALUE + 1
-
-
When evaluated in Java, the expression
2*Double.MAX_VALUEresults inDouble.POSITIVE_INFINITYto indicate that the maximum representable value has been exceeded. However, the expressionDouble.MAX_VALUE + 1results inDouble.MAX_VALUE. Why doesn’t the second case yieldDouble.POSITIVE_INFINITYas well? -
Explain what is printed when the following statements are executed.
System.out.println(15 + 20); System.out.println("15" + 20); System.out.println("" + 15 + 20); -
For each of the following Java expressions, indicate the types of each value being used and the type of the result when the expression is evaluated.
-
3 + 4 -
3 + 4.0 -
3.0 + 4.0 -
3.0f + 4.0 -
(double)(3 + 4) -
(double)(3.0 + 4.0) -
Math.round(3 * 4.2) -
Math.round(3.2 * 4.9) -
Math.round(15.5 * 4.0) -
(int)(15.5 * 4.0) -
Math.round(3.154)
-
-
For each of the following expressions, determine the maximum amount of concurrency that can be achieved. Using a diagram similar to Figure 3.5(b), show how the computation of each expression will proceed. Assume there are no side effects. Note that you can create separate threads for multiple instances of method
f().-
f(a) + f(b) + f(c) -
f(a * g(b)) -
f(g(a)) + f(b) + f(c)
-
-
Answer the following questions about types, values, and references.
-
What is the difference between a value and the type that the value has?
-
In Java, the primitive type
intrepresents a limited set of integers, not the entire set of integers from mathematics. Why is this the case? Why didn’t the designers of Java allowintto represent all integers? -
How are operations defined for reference types?
-
Explain the subtle difference between a reference and an object in Java.
-
-
Consider the following declarations of three
Carobjects.Car car1 = new Car("Mercedes", "C300 Sport", 75000); Car car2 = new Car("Pontiac", "Vibe", 17000); Car car3 = new Car("Mercedes", "C300 Sport", 75000);Let
samebe a variable of typeboolean. What is the value of variablesameafter each of the following statements? Assume that theequals()method will returntrueif all of the attributes specified by the constructors for the two objects are the same.-
same = (car1 == car2); -
same = (car1 == car3); -
same = car1.equals(car3); -
car2 = car3; -
same = (car2 == car1); -
same = (car2 == car3); -
same = car2.equals(car3);
-
-
Characters
'a'and'A'have Unicode values\u0061and\u0041, respectively. Give the representation of these two characters as 16-bit unsigned binary integers. -
Assuming that each character occupies 16 bits (two bytes) in memory and is encoded using Unicode, use hexadecimal numbers to show how the word
"Java"will be represented in computer memory. Unicode values for the Latin alphabet are the same as the values for the older ASCII standard. You can find a listing of these values on many websites such as AsciiTable. -
What is the output from the following sequence of statements?
String p = "Break it"; String q = "down like this!"; System.out.println((p + q).length()); -
What is the output from the following sequence of statements? Note that
rcontains a single space character.String p = "This is not a string."; String q = ""; String r = " "; System.out.println((p + q + r).length());
Programming Practice
-
Try compiling the following program and observe the error reported by the compiler.
public class UninitializedString { public static void main(String[] args) { String greeting; System.out.println(greeting); } }Now initialize the
greetingobject and rerun the program. Why does the program compile now? -
Write a Java program that prompts the user to enter the number of rooms in her home, uses a
Scannerobject to read the input into anintvariable namedrooms, and then outputs the value on the screen. If you compile and execute your program and type in the value3.5, can you explain the output you see? -
Convert the college cost calculator solution given in Section 3.5 to use
JOptionPanemethods for both input and output. Use the header giving the user’s first and last name for the title of the output dialog and omit the line of asterisks. If you put all the output in a singleStringwith a newline (\n) separating each line, the output will display properly.
4. Selection
Life is a sum of all your choices.
4.1. Problem: Monty Hall simulation
There’s a famous mathematical puzzle called the Monty Hall problem, based on the television show Let’s Make a Deal hosted by the eponymous Monty Hall. In this problem, you’re presented with three doors. Two of the three doors have junk behind them. One randomly selected door conceals something like a pile of gold. If you can choose that door, you win the gold. After you make an initial choice, Monty, who knows which door the pile of gold is behind, will open one of the two other doors, always picking a door with junk behind it. If you chose the gold door, Monty will pick between the two junk doors randomly. After opening a door, Monty gives you a chance to switch to the other unopened door. You decide to switch or not, the appropriate door is opened, and you win either junk or a pile of gold, depending on your luck.
As it turns out, it’s always a better strategy to switch doors. If you keep your initial choice, you have a 1 in 3 chance to win the gold. However, if you switch doors, you’ll have a 2 in 3 chance. The problem is counterintuitive and leads many people, including mathematicians and people holding advanced degrees, to the incorrect answer.
Think about it this way: Suppose you could pick two doors to open, and if the gold was behind either one of them, you’d win. Clearly, you’d have a 2 in 3 chance of winning. Monty allows you this option. Just pick the two doors you want and tell Monty the third. He reveals one of your two initial doors as junk, and you switch to the other one.
If you still aren’t convinced, that’s fine. Your goal is to write a program that simulates the Monty Hall dilemma, allowing a user to guess a door and then potentially switch. Once you’ve written the simulation, you can choose to play repeatedly and see how well you do if you switch.
A Monty Hall scenario has two significant features that distinguish it
from problems in previous chapters. First, randomness play a role.
Generating random numbers has become an important part of computer
science, and most languages provide programmers with tools for
generating random or practically random numbers. Recall the Random class
from Chapter 3. With an object of
type Random called random, you can generate a random int between
0 and n - 1 by calling random.nextInt(n).
The second and much more important feature of Java in the solution to this problem is the element of choice. A random door is chosen to hide gold, and the program must react appropriately. The user chooses a door, and the program must carefully choose another door to open in response. Finally, the user must decide whether or not he or she wants to switch his or her choice. Inherent in this problem is the idea of conditional execution. Every program from the previous chapter runs sequentially, line by line. With conditional execution, only some of the code may be executed, depending on input from the user or the values that random numbers take. Previously, every program was deterministic, a series of inevitable consequences. Now, that linear, one-thing-follows-another paradigm has split into complex trees and webs of possible program executions.
4.2. Concepts: Choosing between options
Before we get to random numbers and the complex choices involved in the Monty Hall problem, let’s talk about the simplified approach that most programming languages take to conditional execution. When we come to a point in a program where there is a choice to be made, we can think of it as the question, “Do I want to perform this series of tasks?” Like the classic game of 20 Questions, these questions in Java generally only have two answers: “yes” or “no.” If the answer is “yes,” the program completes Task A, otherwise it completes Task B. It’s easier to design programming languages that can handle yes-or-no questions than any general question. If you’ve studied logic in the past, you have probably run across Boolean logic. Boolean logic gives a set of rules, similar to the rules of traditional algebra, that can be applied to a system with only two values: true and false.
4.2.1. Simple choices
Because we want to build a system using only yes-or-no questions, Boolean logic is a perfect fit for computer science. To conform with other computer scientists, we try to think of conditions in terms of true and false, instead of yes and no. Thus, we can begin to formulate the kinds of choices we want to make:
If it’s raining outside,
I’ll take my umbrella.
This statement is a very simple program, even though it’s not one executed by a computer. The person following this program asks herself, “Is it raining today?” If the answer is “yes,” then she’ll take her umbrella. We can abstract this idea a bit further by saying that raining outside is a condition p and that taking my umbrella is an action a. In other words, if p is true, then do a. We haven’t specified what is to be done if p is not true, although we can assume that the actor in this drama will not take an umbrella.
If we want to view p as a decision to make, we can specify what happens if it’s not true. For example, we could formulate another choice:
If I have at least $50 in my pocket,
I’ll eat a lobster dinner;
otherwise,
I’ll eat fast food.
In this case, we let having at least $50 be condition q, eating a lobster dinner be action b, and eating fast food be action c. Now we’ve created a decision. If q is true, the person will do action b, but if it’s false, she’ll do action c.
4.2.2. Boolean operations
Even by itself, the ability to pick between two options is powerful, but we can augment this ability in a couple of ways. First, we don’t have to rely on simple conditions. Using Boolean logic, we can make arbitrarily complex conditions.
If I’m bored, or it’s late and I can’t sleep,
I’ll watch television.
Someone following this program will watch television if he’s bored or if it’s late and he also can’t sleep. We can break the condition into three sub-conditions: I’m bored is condition x, it’s late is condition y, and I can’t sleep is condition z. We have connected these three conditions together using the words “and” and “or.” These two simple words represent powerful concepts in Boolean logic, AND and OR. When two conditions are combined with AND, the result is true only if both conditions are true. When two conditions are combined with OR, the result is true if either of the conditions is true.
We can create a table called a truth table to show all the possible values certain conditions can take. We’re going to use the symbol ∧ to represent the concept of AND and the symbol ∨ to represent the concept of OR. We’ll also abbreviate true to T and false to F.
Given a condition x, a condition y, and the condition made by x ∧ y, this truth table shows all possible values. As stipulated, x ∧ y is true only when both x and y are true.
| x | y | x ∧ y |
|---|---|---|
T |
T |
T |
T |
F |
F |
F |
T |
F |
F |
F |
F |
This truth table gives all the values for x ∨ y. As you can see, x ∨ y is true if x or y are true.
| x | y | x ∨ y |
|---|---|---|
T |
T |
T |
T |
F |
T |
F |
T |
T |
F |
F |
F |
There’s confusion surrounding the word “or” in English. Sometimes “or” is used in an exclusive sense to mean one or the other but not both, as in, “Would you like lemonade or iced tea with your meal?” In logic, this exclusive or exists as well and is called XOR. This difference gives another reason for a formally structured language like mathematics or Java to express ourselves precisely. When two conditions are connected with XOR, the result is true if one or the other but not both conditions are true. We use the symbol ⊕ to represent the XOR operation in the truth table below.
This truth table gives all the values for x ⊕ y.
| x | y | x ⊕ y |
|---|---|---|
T |
T |
F |
T |
F |
T |
F |
T |
T |
F |
F |
F |
The operations AND, OR, and XOR are all binary operations like addition and multiplication. They connect two conditions together to get a result. There’s also a single unary operation in Boolean logic, the NOT operator. A NOT simply reverses a condition. If a condition is true, then NOT applied to that condition will yield false, and vice versa.
Here’s a truth table for NOT, using the symbol ¬ to represent the NOT operation.
| x | ¬x |
|---|---|
T |
F |
F |
T |
Now that we’ve nailed down some notation for Boolean logic, we can express the complicated expression that sent us down this path in the first place. Recall that x is I’m bored, y is it’s late, and z is I can’t sleep. Let d be the action I’ll watch television. We can express the choice in this way: If x ∨ (y ∧ z), then do d. Using this notation, we’ve expressed precisely the conditions for watching television, using parentheses to clear up the ambiguity present in the original statement. If we can map individual conditions to Boolean variables, we can build conditions of arbitrary complexity.
4.2.3. Nested choices
Making one choice is all well and good, but in life and computer programs, we may have to make many interrelated choices. For example, if you choose to eat at a seafood restaurant, then you might choose between eating shrimp and lobster, but if you choose instead to eat at a steakhouse, the options of shrimp and lobster might not be available.
A nested choice is one that sits inside of another choice you’ve already made. We could describe choices of restaurants and meals as follows.
If I want seafood,
I’ll eat at Sharky’s, where
if I have at least $50,
I’ll order the lobster;
otherwise,
I’ll order the shrimp.
But if I don’t want seafood,
I’ll eat at the Golden Calf, where
if I have at least $30,
I’ll order the filet mignon;
otherwise,
I’ll order the pork chops.
The previous description is long, but it precisely expresses the decisions our imaginary diner might make. This description in English has drawbacks: It’s long and repetitive, and the grouping of specific meal choices with specific restaurants isn’t clear.
In the next section, we discuss Java syntax that allows us to express the same sorts of decision patterns. Unlike English, Java has been designed to make these sequences of decisions clear and easy to read.
4.3. Syntax: Selection in Java
With some theoretical background on the kinds of choices we’re
interested in making, we can now discuss the Java syntax used to
describe these choices. It was no accident that we kept repeating the
word “if,” because the main Java language feature for making choices
is called an if statement.
4.3.1. if statements
The designers of Java studied Boolean logic and created a type called
boolean. Every condition used by an if statement must evaluate to a
boolean value, which can only be one of two things: true or false.
For example, we could have a boolean variable called raining. Stored
in this variable is the value true if it’s raining and false if it
isn’t. Using Java syntax, we could encode our first example in which our
actor takes her umbrella when it’s raining.
if(raining) {
umbrella.take();
}The action taken if it is raining is done by calling a method on an
object. We’ll discuss objects and methods further in
Chapter 8 and Chapter 9. What we’re
focusing on now is that the line umbrella.take(); is executed only if
raining has the value true. Nothing is done if it’s false.
Figure 4.1 shows this pattern of conditional execution
followed by all if statements.

if statement when its condition is true and skips past it otherwise.Our descriptions of logical scenarios from the previous section used the
word “then” to mark the actions that would be done if a condition was
true. Some languages use then as a keyword, but Java doesn’t.
Instead, note the left brace ({) and the right brace (}) that
enclose the executable line umbrella.take();. These braces serve the
same role as the word “then,” clearly marking the action to be
performed if a condition is true. Braces are unambiguous because they
mark a start and an end. If there are many actions to be done, they can
all be put inside the braces, and there will be no question as to which
actions are associated with a given if statement.
For example, we may also need to close the window and put on a raincoat if it’s raining. We might accomplish these tasks in Java as follows.
if(raining) {
umbrella.take();
window.close();
raincoat.putOn();
}Within a matching pair of braces ({ }), called a block of code,
execution proceeds normally, line by line. First, the JVM will cause the
umbrella to be taken, then the window to be closed, and finally the
raincoat to be put on.
If only a single line of code is contained within a block of code, the braces can be left out. For example, many experienced Java programmers would have written our first example as follows.
if(raining)
umbrella.take();For beginning Java programmers, however, it’s a good idea to use braces even when you don’t need to. Without braces, code can appear to be doing one thing when it’s really doing another.
Since programmers must often choose between two alternatives, Java
provides an else statement to specify code that should be run when the
condition of the if statement is false.
Let fiftyDollars be a boolean variable that’s true if we have at
least $50 and is false otherwise. Now, we can choose between two
dining options based on how much money we have.
if(fiftyDollars) {
lobsterDinner.eat();
}
else {
fastFood.eat();
}This Java code matches the logical statements we wrote before. If we
have enough money, we’ll eat a lobster dinner; otherwise, we’ll eat fast
food. As with an if statement, we use braces to mark a block of code
for an else statement, too. Since a single line of code will be
executed in each case, the braces are optional here. We could have
written code with the same functionality as follows.
if(fiftyDollars)
lobsterDinner.eat();
else
fastFood.eat();Figure 4.2 shows the pattern of conditional execution
followed by all if statements that have a matching else statement.

if statement when its condition is true and jumps into the else statement otherwise.|
Pitfall: Misleading indentation
Indentation is used to make code more readable, but Java ignores whitespace, meaning that the indentation has no effect on the execution of the code. To demonstrate, let’s assume that our imaginary diner knows he’ll get a stomachache after eating fast food. Thus, he’ll take some Pepto-Bismol after eating it. If you added this action to the code above, which does not contain braces, you might get the following. Although it looks like both |
4.3.2. The boolean type and its operations
Recall that Java uses the type boolean for values that can only be
true or false. Just like the numerical types double and int, the
boolean type has specific operations that can be used to combine them
together. By design, these operations correspond exactly to the logical
operations we described before. Here’s a table giving the Java
operators equivalent to the logical Boolean operations.
| Name | Math Symbol |
Java Operator |
Description |
|---|---|---|---|
AND |
∧ |
|
Returns |
OR |
∨ |
|
Returns |
XOR |
⊕ |
|
Returns |
NOT |
¬ |
|
Returns the opposite of the value |
Using these operators, we can create boolean values and combine them
together.
boolean x = true;
boolean y = false;
boolean z = !((x || y) ^ (x && y));When this code is executed, the value of z will be false. Although
it’s perfectly legal to perform boolean operations this way, it’s
much more common to combine them “on the fly” inside of the condition
of an if statement. Recall the statement from the previous section:
If I’m bored, or it’s late and I can’t sleep,
I’ll watch television.
If we let bored, late, and canSleep be boolean variables whose
values indicate if we are bored, if it is late, and if we can sleep,
respectively, we can encode this statement in Java like so.
if(bored || (late && !canSleep))
television.watch();Combining the || operator with other || operators is both
commutative and associative: order and grouping doesn’t matter.
Likewise, combining the && operator with other && operators is
also commutative and associative. However, once you start mixing ||
with &&, it’s a good idea to use parentheses for grouping. If, in
the above example, bored is true, late is false, and canSleep
is true, then the expression bored || (late && !canSleep) will be
true. However, with the same values, the expression
bored || late && !canSleep will be false.
Now that we’re discussing ordering, note that ||
and && are short circuit operators. Short circuit means that, if
the value of the expression can be determined without evaluating the
rest of it, the JVM won’t bother to compute any more of the
expression. With || this situation arises because true OR anything
else is still true. With && this situations arises because false
AND anything else is still false.
if(true || ((late && !canSleep && isTired && isHungry) ||
(wantsToFindOutWhatHappensNextInHisFavoriteShow ||
likesTV)))The condition of this if statement will always evaluate to true, and
its body will always be executed. Because Java knows this, it won’t
even bother to check any of the conditions after the first || operator.
This short circuit evaluation is done at run time and will work if the
value of a variable at the beginning of an OR clause is true. It need
not be the literal true.
if(false && ((late || !canSleep || isTired || isHungry) &&
(wantsToFindOutWhatHappensNextInHisFavoriteShow ||
likesTV)))The condition of this if statement will always evaluate to false and
its body won’t be executed. As before, nothing after the first &&
will even be checked. If you’re combining literals and boolean
values with the || and && operators, it makes no difference that
short circuit evaluation occurs. However, if a method call is part of
the clauses, your code might miss valuable side-effects. For example,
let the boolean variable working be false in the following.
if(working && doSomethingImportant())In this case, the doSomethingImportant() method must return a
boolean value to be a valid statement. Still, if working is false,
the doSomethingImportant() method won’t even be called. As soon as the
JVM realizes that it’s applying the && operation to a false
value (or an || to a true), it’ll give up. In many cases, doing so is fine. In fact,
programmers sometimes exploit this feature to allow code in a
method like doSomethingImportant() to run only if it’s safe to do so.
In this case, if we assume that we always want to run the
doSomethingImportant() method (because it does something important)
every time the condition of the if statement is evaluated, we need to
restructure the code. For example, we can reverse the order of the two
terms in the AND clause to achieve this effect. Alternatively, Java
provides non-short circuit versions of the || and && operators,
namely | and &, if you need to force full evaluation.
You might have been wondering where the majority of boolean values come
from. Most computer programs don’t ask the user a long series of true
or false questions before spitting out an answer. Most boolean values
in Java programs are the result of comparisons, often of numerical data
types.
It’s can be useful to compare two numbers to see if one is larger, smaller, or
equal to the other. For example, you might have a double variable
called pressure that gives the water pressure in a hydraulic system.
Perhaps you also have a constant called CRITICAL_PRESSURE that gives
the maximum safe pressure for your system. You can compare these values
using the > operator.
if(pressure > CRITICAL_PRESSURE)
emergencyShutdown();This code allows you to call the appropriate emergency method when
pressure is too high. Of course, the > operator is not the only way
to compare two values in Java. We list all the relational operators in
Chapter 3, but
the table below shows them again in a
mathematical context.
| Name | Math Symbol |
Java Operator |
Description |
|---|---|---|---|
Equals |
= |
|
|
Not Equals |
≠ |
|
|
Less Than |
< |
|
|
Less Than or Equals |
≤ |
|
|
Greater Than |
> |
|
|
Greater Than or Equals |
≥ |
|
|
The concepts and mathematical symbols for these operators should be
familiar from mathematics. There are a few differences from the
mathematical versions of these ideas that are worth pointing out. First,
only easy-to-type symbols are used for Java operators. Thus, we need two
characters to represent most relational operators in the language. These operators
can be used to compare any numerical type with any other numerical type,
including char. In the case of mismatched types, such as an int and
a double, the lower precision type is automatically cast to the higher
precision type. Care should be taken when using the == operator with
floating-point types because of rounding errors. For example, the
expression 1.0/3.0 == 0.3333333333 always evaluates to false.
The == operator is not the same as the = operator from previous
chapters. In Java, the double equal sign == is used to compare two
things while the single equal sign = is used to assign one thing to
another.
Confusion can also arise because, in the mathematical world, relational
symbols are used to make a statement: x < y is an
announcement or a discovery that the value contained in x
is, in fact, smaller than the value contained in y. In the
Java world, the statement x < y is a test whose answer is true if
the value contained in x is smaller than the value contained in y
and false otherwise. Using these operators means performing a test at
a specific point in the code, asking a question about the values that
certain variables or literals (or the results of method calls) have at
that moment in time. In another sense, using these comparisons is a way
to take numerical data and convert it into the language of boolean
values. Note that the following statement does not compile in Java.
if(4)
x = y + z;To be used in an if statement, the value 4 must be first compared
with some other numerical type to yield a true or false.
|
Pitfall: Assignment instead of equality
A common pitfall is to forget one of the equal signs in the comparison operator. Again, this code won’t compile. If it did, the variable Extreme care should be taken when
comparing two This code correctly calls the In this case, |
The next few examples illustrate the use of the if statement. They
also use some methods from class Math.
In the standard Gregorian calendar, leap years occur roughly once every four years. During leap years, the month of February has 29 days instead of 28. This extra day makes up for the fact that it takes a little more than 365.24 days for the earth to orbit the sun. Unfortunately, the orbit of the earth around the sun doesn’t match up in any exact way with the rotation of the earth, making exceptions to the rule of every four years.
In fact, the official definition for a leap year is a year that is evenly divisible by 4, except for those years that are evenly divisible by 100, with the exception to the exception of years that are evenly divisible by 400. For example, 1988 was a leap year because it was divisible by 4. The year 1900 was not a leap year because it was divisible by 100 but not by 400, and the year 2000 was a leap year because it was divisible by 400.
Recall that the mod operator (%) allows us to find the remainder
after integer division. Thus, if n % 100 gives zero, n has no
remainder after being divided by 100 and must be evenly divisible by
100.
import java.util.*;
public class LeapYear {
public static void main(String[] args) {
Scanner in = new Scanner( System.in );
System.out.print("Please enter a year: ");
int year = in.nextInt();
if( year % 400 == 0 )
System.out.println(year + " is a leap year.");
else if( year % 100 == 0 )
System.out.println(year + " is not a leap year.");
else if( year % 4 == 0 )
System.out.println(year + " is a leap year.");
else
System.out.println(year + " is not a leap year.");
}
}As with all of the programs in this section, we begin by importing
java.util.*, which is needed for the Scanner class for input. The
program prompts the user for a year and reads it in. If the year is
evenly divisible by 400, the program outputs that it’s a leap year.
Otherwise, if the year is evenly divisible by 100, the program outputs
that it is not a leap year. Otherwise, if the year is evenly divisible
by 4, the program outputs that it’s a leap year. Finally, if all the
other conditions have failed, the program outputs that the year is not a
leap year.
The quadratic formula is a useful tool from mathematics. Using this formula, you can solve equations of the form ax2 + bx + c = 0. You might recall the statement of the quadratic formula given below.

The b2 - 4ac part of the formula is called the discriminant. If the discriminant is positive, there will be two real answers to the equation. If the discriminant is negative, there will be two complex answers to the equation. Finally, if the discriminant is zero, there will be a single real answer to the problem. If you want to write a program to solve quadratic equations for you, it should take these three possibilities into account.
import java.util.*;
public class Quadratic {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("This program solves quadratic" +
" equations of the form ax^2 + bx + c = 0.");
System.out.print("Please enter a value for a: "); (1)
double a = in.nextDouble();
System.out.print("Please enter a value for b: ");
double b = in.nextDouble();
System.out.print("Please enter a value for c: ");
double c = in.nextDouble();
double discriminant = b*b - 4*a*c; (2)
if(discriminant == 0.0) (3)
System.out.println("The answer is x = " + (-b/(2*a)));
else if(discriminant < 0.0) (4)
System.out.println("The answers are x = " + (-b / (2*a)) + " + "
+ Math.sqrt(-discriminant) / (2*a) + "i and x = "
+ (-b / (2*a)) + " - " + Math.sqrt(-discriminant) / (2*a) + "i");
else (5)
System.out.println("The answers are x = " + (-b + Math.sqrt(discriminant))/(2*a)
+ " and x = " + (-b - Math.sqrt(discriminant))/(2*a));
}
}| 1 | This program prompts the user and reads in values for a,
b, and c. |
| 2 | Then, it computes the discriminant. |
| 3 | In the first case, we test to see if the discriminant is zero and print the single answer. |
| 4 | Next, if the discriminant is negative, we compute the real and complex parts separately and output the two answers. |
| 5 | Finally, if the discriminant is positive, we find the two real answers and output them. |
Note that braces were not needed for the if,
else-if, and else blocks because each is composed of only a single
line of code. Although these System.out.println() method calls may
take up more than one line visually, Java interprets them as single
lines because they each only have a single semicolon (;).
The line if(discriminant == 0.0) is dangerous since we’re using
double values. Because of rounding errors, the discriminant might not
be exactly zero even if it should be, mathematically. Industrial
strength code would probably check to see if the absolute value of the
discriminant is less than a very small number (such as 0.00000001).
Values that small would then be treated as if they were zero.
In the time-honored game of 20 Questions, one person mentally chooses something, and the other participants must guess what the thing is by asking questions whose answer is either “yes” or “no.” In one popular version, the person who chooses the thing starts by declaring whether it is animal, vegetable, or mineral.
Using counting principles from math, 20 yes-or-no questions makes it possible to differentiate 220 = 1,048,576 items. If you’re also told whether the thing is animal, vegetable, or mineral, it should be possible to guess over 3 million items! At this point in our development as Java programmers, we’re not yet ready to deal with such a large range of possibilities. To keep the size of the code reasonable, let’s narrow the field to 10 different items: a lizard, an eagle, a dolphin, a human, some lead, a diamond, a tomato, a peach, a maple tree, and a potato.

Using these items, we can construct a tree of decisions, starting with the decision between animal, vegetable, and mineral. If the thing is an animal, we could then ask if it is a mammal. If it is a mammal, we could ask if it lives on land, deciding between human and dolphin. If it’s not a mammal, we could ask if it flies, deciding between an eagle and a lizard. We can construct similar questions for the things in the vegetable and mineral categories, matching Figure 4.3.
import java.util.*;
public class TwentyQuestions {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("Is it an animal, vegetable, or mineral? (a, v, or m): ");
String response = in.next().toLowerCase();
if(response.equals("a")) {
System.out.print("Is it a mammal? (y or n): ");
response = in.next().toLowerCase();
if(response.equals("y")) {
System.out.print(
"Does it live on land? (y or n): ");
response = in.next().toLowerCase();
if(response.equals("y"))
System.out.println("It's a human.");
else // Assume "n"
System.out.println("It's a dolphin.");
}
else { // Assume "n"
System.out.print("Does it fly? (y or n): ");
response = in.next().toLowerCase();
if(response.equals("y"))
System.out.println("It's an eagle.");
else // Assume "n"
System.out.println("It's a lizard.");
}
}
else if(response.equals("v")) {
System.out.print("Is it a fruit? (y or n): ");
response = in.next().toLowerCase();
if(response.equals("y")) {
System.out.print(
"Does it grown on a vine? (y or n): ");
response = in.next().toLowerCase();
if(response.equals("y"))
System.out.println("It's a tomato.");
else // Assume "n"
System.out.println("It's a peach.");
}
else { // Assume "n"
System.out.print("Is it a tree? (y or n): ");
response = in.next().toLowerCase();
if(response.equals("y"))
System.out.println("It's a maple tree.");
else // Assume "n"
System.out.println("It's a potato.");
}
}
else { // Assume "m"
System.out.print(
"Is it the hardest mineral? (y or n): ");
response = in.next().toLowerCase();
if(response.equals("y"))
System.out.println("It's a diamond.");
else // Assume "n"
System.out.println("It's lead.");
}
}
}The code in this example is straightforward, although even 10 items
makes for a lot of if and else blocks. Other than the if-else
statements, only simple input and output are needed to make the program
function. For proper String comparison, it’s necessary to use the
equals() method to test if two String values are the same.
Note that we’ve added comments specifying what we assume is the case
for each else block. If we were being more careful, we should test for
the "y" and "n" cases and then give an error message when the user
inputs something unexpected, like "x" or "149" or even "no".
Again, note that no braces are needed for the final if-else blocks
in which the guess is made, since each of these guesses requires only a
single line of code.
You might be curious how to make a real 20 Questions game that could learn over time. To do so, many more programming tools are necessary: repetition, data structures (so that you can organize the questions), and file input and output (so that you can store new information permanently). These concepts are covered in later chapters.
4.3.3. switch statements
The if statement is the workhorse of Java conditional execution. With
enough care, you can craft code that can make any fixed sequence of
decisions with arbitrary complexity. Even so, the if statement can be
a little clumsy because it only allows you to choose between two
alternatives. After all, a conditional can only be true or false.
Certainly, decisions can be nested, allowing for more than two
possibilities, but long lists of possibilities can be cumbersome and hard to read.
For example, imagine that we want to create a program that determines the appropriate gift for a wedding anniversary. Below is a table of traditional categories of gifts based on the anniversary year.
| Year | Gift | Year | Gift | |
|---|---|---|---|---|
1 |
Paper |
13 |
Lace |
|
2 |
Cotton |
14 |
Ivory |
|
3 |
Leather |
15 |
Crystal |
|
4 |
Fruit |
20 |
China |
|
5 |
Wood |
25 |
Silver |
|
6 |
Candy / Iron |
30 |
Pearl |
|
7 |
Wool / Copper |
35 |
Coral |
|
8 |
Bronze / Pottery |
40 |
Ruby |
|
9 |
Pottery / Willow |
45 |
Sapphire |
|
10 |
Tin / Aluminum |
50 |
Gold |
|
11 |
Steel |
55 |
Emerald |
|
12 |
Silk / Linen |
60 |
Diamond |
Let year be a variable of type int containing the year in question.
A structure of if-else statements that can determine the appropriate
gift based on the year is below.
String gift;
if(year == 1)
gift = "Paper";
else if(year == 2)
gift = "Cotton";
else if(year == 3)
gift = "Leather";
else if(year == 4)
gift = "Fruit";
else if(year == 5)
gift = "Wood";
else if(year == 6)
gift = "Candy / Iron";
else if(year == 7)
gift = "Wool / Copper";
else if(year == 8)
gift = "Bronze / Pottery";
else if(year == 9)
gift = "Pottery / Willow";
else if(year == 10)
gift = "Tin / Aluminum";
else if(year == 11)
gift = "Steel";
else if(year == 12)
gift = "Silk / Linen";
else if(year == 13)
gift = "Lace";
else if(year == 14)
gift = "Ivory";
else if(year == 15)
gift = "Crystal";
else if(year == 20)
gift = "China";
else if(year == 25)
gift = "Silver";
else if(year == 30)
gift = "Pearl";
else if(year == 35)
gift = "Coral";
else if(year == 40)
gift = "Ruby";
else if(year == 45)
gift = "Sapphire";
else if(year == 50)
gift = "Gold";
else if(year == 55)
gift = "Emerald";
else if(year == 60)
gift = "Diamond";
else
gift = "No traditional gift";This code stores the correct value in gift. Note that we are using the
feature of if statements that treats an entire if statement as one
statement. If we used braces to group things properly, the code would
become unreadable and unmanageably large.
String gift;
if(year == 1) {
gift = "Paper";
}
else {
if(year == 2) {
gift = "Cotton";
}
else {
if(year == 3) {
gift = "Leather";
}
else {
if(year == 4) {
gift = "Fruit";
}
.
.
.It appears that there’s some kind of else if construct in Java, but
there isn’t. Still, careful use of the rules for braces allows us to
write code that nicely expresses a sequence of alternatives.
Another way of expressing a long sequence of alternatives is by using a
switch statement. A switch statement takes a single integer type
value (int, long, short, byte, char) or a String and jumps
to a case corresponding to the input. We can recode the anniversary gift
example using a switch statement as follows.
String gift;
switch(year) {
case 1: gift = "Paper"; break;
case 2: gift = "Cotton"; break;
case 3: gift = "Leather"; break;
case 4: gift = "Fruit"; break;
case 5: gift = "Wood"; break;
case 6: gift = "Candy / Iron"; break;
case 7: gift = "Wool / Copper"; break;
case 8: gift = "Bronze / Pottery"; break;
case 9: gift = "Pottery / Willow"; break;
case 10: gift = "Tin / Aluminum"; break;
case 11: gift = "Steel"; break;
case 12: gift = "Silk / Linen"; break;
case 13: gift = "Lace"; break;
case 14: gift = "Ivory"; break;
case 15: gift = "Crystal"; break;
case 20: gift = "China"; break;
case 25: gift = "Silver"; break;
case 30: gift = "Pearl"; break;
case 35: gift = "Coral"; break;
case 40: gift = "Ruby"; break;
case 45: gift = "Sapphire"; break;
case 50: gift = "Gold"; break;
case 55: gift = "Emerald"; break;
case 60: gift = "Diamond"; break;
default: gift = "No traditional gift"; break;
}Just like an if statement, a switch statement always has parentheses
enclosing some argument. Unlike an if, the argument of a switch must
be some kind of data that can be expressed as an integer or a String,
not a boolean. For each of the possible values you want the switch
to handle, you write a case statement. A case statement consists of
the keyword case followed by a constant value, either a literal or a
named constant, then a colon. When executed, the JVM jumps to the
matching case label and starts executing code there. If there is no
matching case label, the JVM goes to the default label. If there is
no default label, the entire switch statement is skipped.
One unusual feature of switch statements is that execution falls
through case statements. This means that you can use many different
case statements for a single segment of executable code. The execution
of code in a switch statement jumps out when it hits a break
statement. However, break statements are not required, as shown in
this switch statement that gives location information for all of the
telephone area codes in New York state.
String location = "";
switch(code) {
case 917: location = "Cellular: ";
case 212:
case 347:
case 646:
case 718: location += "New York City"; break;
case 315: location = "Syracuse"; break;
case 516: location = "Nassau County"; break;
case 518: location = "Albany"; break;
case 585: location = "Rochester"; break;
case 607: location = "South Central New York"; break;
case 631: location = "Suffolk County"; break;
case 716: location = "Buffalo"; break;
case 845: location = "Lower Hudson Valley"; break;
case 914: location = "Westchester County"; break;
default: location = "Unknown Area Code"; break;
}As you can see, five different area codes are used by New York City. By
leaving out the break statements, values of 212, 347, 646, and
718 all have "New York City" stored into location. Area code 917
was originally designated for cellular phones and pagers although now it
includes some landlines. By cleverly putting the statement for 917 ahead of
the other New York City entries, a value of 917 first stores
"Cellular: " into location and then falls through and appends
"New York City". For each of these five area codes, execution in the
switch statement ends only when the break statement is reached.
The remaining nine area codes are separate. Each of them does a
single assignment and then breaks out of the switch block. Finally,
the default label is used if the area code doesn’t match one of the
given codes. Note that we’ve ordered the (non-NYC) area codes in
ascending order for the sake of readability. As shown in the
917 example, there’s no rule about the ordering of the labels. Even
the default label can occur anywhere in the switch block you want,
although it’s common to put it at the end. Also, the break after the
default label is unnecessary because execution exits the switch
block anyway. Nevertheless, it’s always wise to end on a break, in
the event that you add more cases in later.
Carelessness is always something to watch out for in switch
statements. Leaving out a break statement can cause disastrous and
difficult to discover bugs. The compiler does not warn you about missing
break statements, either. It’s entirely your responsibility to use them
appropriately. Because of the dangers involved, it’s often safe to
use if-else statements. Any switch statement can be rewritten as
some combination of if-else statements, but the reverse is not true.
The benefit of switch statements is their ability to list many
alternatives clearly. Their drawbacks include the ease of making a
mistake, an inability to express ranges of data or most types (double,
float, or any reference type other than String), and limited
expressive power. They should be used only when their benefit of clearly
displaying a list of data outweighs the drawbacks.
Next we give a number of examples to help you get more familiar with
switch statements.
There are fewer uses for switch statements than if statements.
Nevertheless, there are problems where their
fall-through behavior can be useful. Imagine that you need to write a
program that gives the length of each month (with the assumption that February always
has 28 days). Given the month as a number, we can use switch statements to write a program
that maps the number of the month to the number of days it contains.
import java.util.*;
public class DaysInMonth {
public static void main(String[] args) {
Scanner in = new Scanner( System.in );
System.out.print("Please a month number (1-12): ");
int month = in.nextInt();
int days = 0;
switch( month ) {
case 2: days = 28; break; (1)
case 4:
case 6:
case 9:
case 11: days = 30; break; (2)
case 1:
case 3:
case 5:
case 7:
case 8:
case 10:
case 12: days = 31; break; (3)
}
System.out.println("The month you entered has " + days + " days.");
}
}| 1 | This program has a single label for February setting days to 28. |
| 2 | Then, there are labels for April, June, September, and November, months that each have 30 days. |
| 3 | Finally, the large block of January, March, May,
July, August, October, and December all set days to 31. |
It would be
easy to extend this code to prompt the user for a year so that you could
integrate the leap year code from above for the February case. Note also
that we didn’t use a default label. You might want to set days to
some special value (like -1) for invalid months.
In this program it’s necessary to initialize days to some value, in this case 0.
Otherwise, the program won’t compile, since it’ll try to print out the
value inside days, a value that won’t exist if month is not in the range 1 through 12.
The term ordinal numbers refers to numbers that are used for ordering within a set of items: first, second, third, and so on. When writing these numbers with numerals in English, it is common to append two letters to the end of the numeral to give the reader a clue that these numerals should be read with their ordinal names: 1st, 2nd, 3rd, and so on.
Unlike most things in English, the rules for deciding which two letters
are relatively simple. If the number ends in a 1, the letters “st”
should generally be used. If the number ends in a 2, the letters “nd”
should generally be used. If the number ends in a 3, the letters “rd”
should generally be used. For most other numbers, the letters “th”
should be used. We can use a switch statement to write a program to
give the correct ordinal endings for most numbers as follows.
import java.util.*;
public class Ordinals {
public static void main(String[] args) {
Scanner in = new Scanner( System.in );
System.out.print("Please enter a positive number: ");
int number = in.nextInt();
String ending;
switch( number % 10 ) {
case 1: ending = "st"; break;
case 2: ending = "nd"; break;
case 3: ending = "rd"; break;
default: ending = "th"; break;
}
System.out.println("Its ordinal version is "
+ number + ending + ".");
}
}This program prompts and then reads in an int from the user. We then
find the remainder of number when it’s divided by 10, yielding its
last digit. Based on this digit, we can pick from the four possibilities
and output the correct ordinal number in most cases. Unfortunately, the
names for English numbers have an inconsistent naming convention between 11 and 19, inclusive,
and the ordinals for any number ending in 11, 12, or 13 will be given the wrong
suffix by our code. We leave a more complete solution as an exercise.
Many cultures practice astrology, a tradition that the time of a person’s birth impacts his or her personality or future. One important element of Chinese astrology is their zodiac, consisting of 12 animals. Each consecutive year in a 12-year cycle corresponds to an animal. Because this system repeats, the year one is born in modulo 12 identifies the animal. Below is a table giving these values. For example, if you were born in 1979, 1979 mod 12 ≡ 11; thus, you would be a Ram. Note that this arrangement is based on years in the Gregorian calendar. Chinese astrologers do not list the Monkey as the first animal in the cycle. Note that the names of these animals are also sometimes translated in slightly different ways.
| Animal | Year modulo 12 |
Animal | Year modulo 12 |
|
|---|---|---|---|---|
Monkey |
0 |
Tiger |
6 |
|
Rooster |
1 |
Rabbit |
7 |
|
Dog |
2 |
Dragon |
8 |
|
Boar |
3 |
Snake |
9 |
|
Rat |
4 |
Horse |
10 |
|
Ox |
5 |
Ram |
11 |
Unfortunately, this table is not very accurate because it’s based on
numbering from the Gregorian calendar. The years in question actually
start and end based on Chinese New Year, which occurs between January 21
and February 20. As a consequence, you may miscalculate your animal if
your birthday is early in the year. Since calculating the date of
Chinese New Year is challenging, let’s ignore this problem for the
moment and write a program using a switch statement designed to
correctly output the animal corresponding to an input birth year.
import java.util.*;
public class ChineseZodiac {
public static void main(String[] args) {
Scanner in = new Scanner( System.in );
System.out.print("Please enter a year: ");
int year = in.nextInt();
String animal = "";
switch( year % 12 ) {
case 0: animal = "Monkey"; break;
case 1: animal = "Rooster"; break;
case 2: animal = "Dog"; break;
case 3: animal = "Boar"; break;
case 4: animal = "Rat"; break;
case 5: animal = "Ox"; break;
case 6: animal = "Tiger"; break;
case 7: animal = "Rabbit"; break;
case 8: animal = "Dragon"; break;
case 9: animal = "Snake"; break;
case 10: animal = "Horse"; break;
case 11: animal = "Ram"; break;
}
System.out.println("The Chinese zodiac animal for this year is: " + animal);
}
}| Sign | Symbol | Date Range |
|---|---|---|
Aries |
The Ram |
March 21 to April 19 |
Taurus |
The Bull |
April 20 to May 20 |
Gemini |
The Twins |
May 21 to June 20 |
Cancer |
The Crab |
June 21 to July 22 |
Leo |
The Lion |
July 23 to August 22 |
Virgo |
The Virgin |
August 23 to September 22 |
Libra |
The Scales |
September 23 to October 22 |
Scorpio |
The Scorpion |
October 23 to November 21 |
Sagittarius |
The Archer |
November 22 to December 21 |
Capricorn |
The Sea-Goat |
December 22 to January 19 |
Aquarius |
The Water Bearer |
January 20 to February 19 |
Pisces |
The Fishes |
February 20 to March 20 |
In Western astrology, an important element associated with a person’s birth is also called a zodiac sign. The dates for determining this kind of zodiac sign are given by the preceding table.
If you want to implement the rules for this zodiac in code, a switch
statement is a good place to start, but you also have to put if
statements for each month to test the exact range of dates.
import java.util.*;
public class WesternZodiac {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("Please enter a month number (1-12): ");
int month = in.nextInt();
System.out.print("Please enter a day number in that month (1-31): ");
int day = in.nextInt();
String sign = "";
switch(month) {
case 1: if(day < 20)
sign = "Capricorn";
else
sign = "Aquarius";
break;
case 2: if(day < 20)
sign = "Aquarius";
else
sign = "Pices";
break;
case 3: if(day < 20)
sign = "Pices";
else
sign = "Aries";
break;
case 4: if(day < 20)
sign = "Aries";
else
sign = "Taurus";
break;
case 5: if(day < 21)
sign = "Taurus";
else
sign = "Gemini";
break;
case 6: if(day < 21)
sign = "Gemini";
else
sign = "Cancer";
break;
case 7: if(day < 23)
sign = "Cancer";
else
sign = "Leo";
break;
case 8: if(day < 23)
sign = "Leo";
else
sign = "Virgo";
break;
case 9: if(day < 23)
sign = "Virgo";
else
sign = "Libra";
break;
case 10:if(day < 23)
sign = "Libra";
else
sign = "Scorpio";
break;
case 11:if(day < 22)
sign = "Scorpio";
else
sign = "Sagittarius";
break;
case 12:if(day < 20)
sign = "Sagittarius";
else
sign = "Capricorn";
break;
}
System.out.println("The zodiac sign is: " + sign);
}
}This program is just slightly more complex than the program for the Chinese zodiac. You still need to jump to 12 different cases (numbered 1-12 instead of 0-11), but additional day information is needed to pin down the sign.
4.4. Solution: Monty Hall
We now return to the Monty Hall simulation described at the beginning of
the chapter. Recall that objects of the Random class allow us to generate all
kinds of random values. To implement this simulation successfully, our
program must make the decisions needed to set up the game for the
user as well as respond to the user’s input.
import java.util.*; (1)
public class MontyHall {
public static void main(String[] args) {
Random random = new Random();
int winner = random.nextInt(3); (2)
Scanner in = new Scanner( System.in );
System.out.print("Choose a door (enter 0, 1, or 2): ");
int choice = in.nextInt(); (3)
int alternative; (4)
int open;| 1 | We begin with the import
statement needed to use both the Scanner and Random class
and then define the MontyHall class. |
| 2 | In the main() method we first decide which of the three doors is the
winner. To do so, we instantiate a Random object and use it to
generate a random number that is either 0, 1, or 2 by calling the
nextInt() method with an argument of 3. We could have added 1 to
this value to get a random choice of 1, 2, or 3, but many counting
systems in computer science start with 0 instead of 1. We might as well
embrace it. |
| 3 | Next, we prompt the user to pick from the three doors and read the choice. |
| 4 | Finally, we declare two more int values to keep
track of which door to open and which door is the alternative that the
user can choose to change over to. |
Now, we have to navigate a complicated series of decisions.
if( choice == winner ) { (1)
int low;
int high;
if( choice == 0 ) { (2)
low = 1;
high = 2;
}
else if( choice == 1 ) {
low = 0;
high = 2;
}
else { //choice == 2
low = 0;
high = 1;
}
//randomly choose between other two doors
double threshold = random.nextDouble(); (3)
if( threshold < 0.5 ) { (4)
alternative = low;
open = high;
}
else { (5)
alternative = high;
open = low;
}
}| 1 | In this segment of code, we tackle the possibility that the user happened to choose the winning door. To obey the rules of the game, we must randomly pick which of the two other doors to open. |
| 2 | First, we determine
which are the other two doors and save them in low and high,
respectively. |
| 3 | Then, we generate a random number. |
| 4 | If the random number is less than 0.5, we keep the lower numbered door as an alternative choice for the user and open the higher numbered door. |
| 5 | If the random number is greater than or equal to 0.5, we do the opposite. |
else { (1)
alternative = winner;
if( choice == 0 ) { (2)
if( winner == 1 )
open = 2;
else
open = 1;
}
else if( choice == 1 ) {
if( winner == 0 )
open = 2;
else
open = 0;
}
else { //choice == 2
if( winner == 0 )
open = 1;
else
open = 0;
}
}| 1 | This else block covers the case that the player did not pick the
winning door the first time. Unlike the previous code segment, we no
longer have a choice of which door to open. |
| 2 | Instead, we must always make the winner the alternative for the user to pick. Then, we simply determine which door is left over so that we can open it. |
Note that the
braces surrounding the blocks for each of the braces surrounding the
blocks for each of the three possible values of choice are not
necessary but are included for readability.
System.out.println("We have opened Door " + open + (1)
", and there is junk behind it!");
System.out.print("Do you want to change to Door " + (2)
alternative + " from Door " + choice +
"? (Enter 'y' or 'n'): ");
String change = in.next();
if( change.equals("y") )
choice = alternative;
System.out.println("You chose Door " + choice);
if( choice == winner ) (3)
System.out.println("You win a pile of gold!");
else
System.out.println("You win a pile of junk.");
}
}| 1 | This final segment of code informs the user which door has been opened. |
| 2 | It prompts the user to change his or her decision. |
| 3 | Depending on the final choice, the program says whether or not the user wins gold or junk. |
4.5. Concurrency: Selection
Selection statements (if and switch) seem to have
little to do with concurrency or parallelism. Selection allows you to
choose between alternatives while concurrency is about the interaction
between different threads of execution. As it turns out, there are two
reasons why selection and concurrency are deeply related to each other.
The first reason is that selection is one of the most basic tools in
Java. It’s impossible to go more than a few lines of a code without
encountering a selection statement, usually an if.
Concurrent programs are not exempt from this dependence on if
statements. Making decisions is at the heart of all programming
languages running on all computers.
The second, more troubling reason is related to a problem with
some concurrent programs called a race condition, which is discussed
in detail in Chapter 14. Remember, one of
the biggest challenges of programming a computer is thinking in a
completely sequential and logical way. Each line of code is executed one
after the other. Adding in if statements means that some code is
executed only if a condition is true and skipped otherwise. Consider the
following fragment of code:
if(!matches.areLit() && !flyingSparks) {
storageRoom.enter();
dynamite.unpack();
}In this if statement, an imaginary agent only enters the storage room
and unpacks the dynamite if the matches are not lit and there are no
flying sparks. When execution reaches the first line inside the if
block, we are certain that matches.areLit() returned false and
flyingSparks is false. This is a one-time check. If the first thing
that happens inside the if block is code that lights the matches, Java
will not jump out of the if statement.
As always, the programmer is responsible for making an if statement
that makes sense. It’s possible that entering the storage room or
unpacking the dynamite causes sparks to fly or matches to burst into
flames spontaneously, but it seems unlikely. If the storageRoom and
dynamite objects were written by other people, we would expect their
documentation to explain unusual side-effects of this kind. In a
sequential program, the programmer can be reasonably sure that it’s
safe to unpack the dynamite.
Consider another fragment of code:
matches.light();
flyingSparks = sparklers.light(matches);This code appears to light the matches and then to use the lit matches to set
some sparklers on fire. Presumably, if the process was successful,
flyingSparks will have the value true. This code is reasonable and
potentially helpful. If you were celebrating the 4th of July or needed
to signal a passing helicopter to rescue you from a desert island,
lighting sparklers could be a great idea. This sparkler-lighting code
could occur before the dynamite-unpacking code or after it, but, in a sequential
program, the protection of the if statement keeps our hero from being blown up if
she tries to unpack the dynamite with lit sparklers.
In a concurrent program, all bets are off. Another thread of execution
can be operating at the very same time. It’s as if our hero is trying to
unpack the dynamite while the villain is lighting sparklers and tossing
them into the storage room. If the thread of execution gets to the if
statement and makes sure that the matches aren’t lit and that there are
no flying sparks, it continues onward. If sparks start flying after that
check, it still continues onward, oblivious of the fact. Even though
this risk of explosion exists, it depends on the timing of the two (or
more) concurrent threads of execution. It might be possible to run a
program 1,000 times with no problem. But if the timing is wrong on the
1,001st time, BOOM!
At this point, you don’t need to worry about values inside your if
statements being changed by other segments of code, but that problem is
at the heart of why concurrent programming can be so difficult. Whether
or not you’re programming concurrently, it’s important to keep
in mind the assumptions your code makes and the way different parts of
your program interact with each other.
4.6. Exercises
Conceptual Problems
-
Given that x, y, and z are propositions in Boolean logic, make a truth table for the expression ¬(x ∧ ¬y) ⊕ ¬z.
-
What’s the value of the Boolean expression ¬( (T ⊕ F) ∧ ¬(F ∨ T) )?
-
The calculation to determine the leap year given in Example 4.1 uses three
ifstatements and threeelsestatements. Write the leap year calculation using a singleifand a singleelse. Feel free to usebooleanconnectors such as||and&&. -
The XOR operator (
^) is useful for combiningbooleanvalues, but it can be replaced with a more commonly used relational operator in Java. Which one? -
De Morgan’s laws are the following, which show that the process of negating a clause changes an AND to an OR and vice versa.
¬(x ∧ y) = ¬x ∨ ¬y
¬(x ∨ y) = ¬x ∧ ¬yCreate truth tables to verify both of these statements.
-
Use De Morgan’s laws given above to rewrite the following statement in Java to an equivalent statement that contains no negations.
boolean value = !((x != 4) && (y < 2)); -
Consider the following fragment of code.
int x = 5; int y = 3; if(y > 10 && (x = 10) > 5) y++; System.out.println("x: " + x); System.out.println("y: " + y);What’s the output? Is the output changed if the condition of the
ifstatement is changed toy > 10 & (x = 10) > 5? Why? -
Consider the following fragment of code.
int a = 7; if(a++ == 7) System.out.println("Seven"); else System.out.println("Not seven");What’s the output? Is the output changed if the condition of the
ifstatement is changed to++a == 7? Why?
Note: It is generally wise to avoid increment, decrement, and assignment statements in the condition of anifstatement because of the confusion that can arise.
Programming Practice
-
Write programs that:
-
Read in two
doublevalues and print the larger of the two of them. -
Read in three
doublevalues and print the largest of the three out. Note: You should use nestedifstatements.
-
-
-
Read an
intvalue from the user specifying a certain number of cents. Useifstatements to print out the name of the corresponding coin in U.S. currency according to the table below. If the value doesn’t match any coin, printno coin.Cents Coin 1
penny
5
nickel
10
dime
25
quarter
50
half-dollar
100
dollar
-
Read a
Stringvalue from the user that gives one of the 6 coin names given in the table above. Useifstatements to print out the corresponding number of cents for the input. If the name doesn’t many any coin, printunknown coin.
-
-
Re-implement both parts from Exercise 4.10 using
switchstatements instead ofifstatements. -
Expand the program given in Example 4.5 to give the correct suffixes (always “th”) for numbers that end in 11, 12, and 13. Use the modulus operator to find the last two digits of the number. Using an
ifstatement, aswitchstatement, or a combination, check for those three cases before going into the normal cases. -
At the bottom of Section 4.3.3, we use a
switchstatement to determine the location of various area codes in New York state. Write an equivalent fragment of code usingif-elsestatements instead. -
Every member of your secret club has an ID number. These ID numbers are between 1 and 1,000,000 and have two special characteristics: They are multiples of 7 and all end with a 3 in the one’s place. For example, 63 is the smallest such value, and 999,943 is the largest such value. Write a program that prompts the user for an
intvalue, reads it in, and then says whether or not it could be used as an ID number. Note: You need to use the modulus operator in two different ways to test the value correctly. -
According to the North American Numbering Plan (NANP) used by the United States, Canada, and a number of smaller countries, a legal telephone number takes the form
XYY-XYY-YYYY, whereXis any digit 2-9 andYis any digit 0-9. Write a program that reads in aStringfrom the user and verifies that it is a legal NANP phone number. The length of the entireStringmust be 12. The fourth and eight characters in theString(with indexes3and7) must be hyphens (-), and all the remaining digits must be in the correct range. Use thecharAt()method of theStringclass to get thecharvalue at each index. Note: There are several ways to structure theifstatements you need to use, but the number of conditions may become large. (23 or more!) -
Re-implement the solution to the Monty Hall program given in Section 4.4 using
JOptionPaneto generate GUIs for input and output.
5. Repetition
Q-Tip: You on point, Phife?
Phife Dawg: All the time, Tip.
Q-Tip: You on point, Phife?
Phife Dawg: All the time, Tip.
Q-Tip: You on point, Phife?
Phife Dawg: All the time, Tip.
Q-Tip: Well, then grab the microphone and let your words rip.
5.1. Problem: DNA searching
The world of bioinformatics is the intersection between biology and computer science. Sequencing genomes, determining the function of specific genes, the analysis and prediction of protein structures, and biomedical imaging are just a few of the areas under the umbrella of bioinformatics. Much fascinating research is being done in this area as biologists become better programmers and computer scientists apply their techniques to biology.
Because of its fundamental importance and the incredible amount of information involved, with tens or hundreds of millions of base pairs of DNA in each human chromosome, DNA is a central focus of bioinformatics. As you may know, a DNA strand is made up of a sequence of four nucleotide bases: adenine, cytosine, guanine, and thymine. These bases are usually abbreviated as A, C, G, and T, respectively.
Searching for a specific DNA subsequence within a larger sequence is a common task for biologists to perform. Your goal is to write a program that will search for a subsequence and report how many times it was found within the sequence. For example, if you are given the sequence ATTAGACCATATA and asked to search for CAT, your program should output 1, since there is exactly 1 occurrence of CAT within ATTAGACCATATA. One feature of this problem that makes it more interesting is that occurrences can overlap. For example, given the sequence TATTATTAGATTA and asked to search for TATTA, the correct answer is 2. The sequence begins with a TATTA, but the third T in the sequence is also the first T in a second instance of TATTA.
In Chapter 4, you learned tools that allow you to do
comparisons and make choices based on the results. These tools will
become even more useful. For example, when you come across a char in a
sequence, you know how to compare it to a char in the subsequence you
are searching for. The tools you do not yet have are those that allow
repetition. Because this problem requires the program to process a DNA
sequence of arbitrary length, we will need some way to perform an
action repeatedly.
5.2. Concepts: Repetition
You now know how to write choices into a Java program, but so far, each choice can only be made once. So if you want the computer to do a lot of things, you have to type a lot of things. One of the big disadvantages of computers is that they have no intelligence: They can follow instructions blindly, but they can’t do anything else. One of the big advantages of computers is that they’re fast. Modern computers can perform mathematical operations billions of times faster than human beings. To take advantage of this speed, we need to give computers instructions to perform tasks over and over. Such an instruction must have two components to be useful: It must have a way to change the task slightly each time so that each task accomplishes something different. It must also have a way to decide when to stop, otherwise it will continue forever.
The first component is the more subtle one. Crafting a set of instructions so that each repetition of the task is appropriate will be different for every problem. The second component is easier to describe: We’re going to rely on Boolean logic, just as we did for conditional statements. The main tool for repetition in Java and many other languages is called a loop. The body of a loop contains the task to be performed. The rest of the loop, at the very least, contains a condition. Every time the task given in the body of the loop completes, the computer will check the condition. If the condition is true, it’ll do the task again. If the condition is false, the computer is done with the loop and can move on to the code that comes afterward.
One of the difficulties of programming a computer is that we must be very explicit. Even the most obvious tasks must be spelled out in meticulous detail. Let’s consider a simple task, one that we perform every day. If we’re in a room and we want to leave, we simply walk out the nearest door. Assuming there is only one door in the room, how can we describe this process by breaking it down into the steps we (literally) take? Perhaps we could say the following.
Walk toward the door until you reach it.
This statement is a little more specific than Leave the room, but it doesn’t conform nicely to the paradigm of a loop, that is, a clearly separated task and a condition. The following is better.
While you’re not at the door,
take a step toward the door.
Now we have good separation between the work done and the condition for repeating. What’s the task performed in the body of this loop, and what’s the condition? The task is taking a step toward the door. The condition is not being at the door. It seems a little awkward to include that “not,” but in our definition of loops, the body is executed as long as the condition is true.
In a loop, we call each execution of the body of the loop an iteration. When we say that a program iterates over the statements in a loop, we are referring to a single pass through the body of a loop. In this case, the loop will iterate however many times there are steps to the door from the starting position. It is even possible that the loop will iterate zero times: The person following this set of instructions might already be at the door!
It’s hard to get away from numbers in a computer program, especially since everything is fundamentally stored as numbers inside of a computer. So, the most common kind of loop is one that iterates a fixed number of times. For example, your morning exercise routine might include jumping rope 100 times. We could formulate a loop to do that like so.
Set your counter to 0.
While your counter is less than 100,
jump rope.
Increase your counter by 1.
This loop requires set up to start the counter at the right value. Then, the work done by the loop is the actual rope jumping and the counter increment. The condition is the counter being less than 100. Note that this is strictly less than 100. After the first jump, the counter will be incremented to 1. After the 100th jump, the counter will be incremented to 100. Since 100 is not less than 100, the loop will exit. If the condition was the counter being less than or equal to 100, the person following the instructions would jump 101 times.
Input can also be a factor in loop repetitions. For example, you might
be a soldier training in the U.S. Marine Corps. Perhaps your drill
sergeant has commanded you to do push-ups until he says you can stop. We
might formulate a loop to do this as follows.
Do:
Push-up.
Ask the drill sergeant if you can stop.
While the answer is “no.”
As is the case with user input, you must often go into the loop at least once to get the input. This loop requires the soldier to do at least one push-up before asking to stop. Some systems might use input but have other constraints. A more realistic version of this loop might be the following.
Do:
Push-up.
Ask the drill sergeant if you can stop.
While the answer is “no” and you haven’t collapsed.
Remember, the condition for a loop should be a Boolean, and the loop runs as long as the condition is true. However, there is no reason why the Boolean can’t be a complicated expression using all the Boolean logic we have come to know and love.
It’s also possible to nest loops. Nesting loops means putting one loop inside of another, similar to the way that conditional statements could be nested inside of other conditional statements. Just like any other statement, an inner loop will be run as many times as the outer loop runs. Of course, the statements inside of the inner loop will be run according to the conditions of that loop. So, if an outer loop runs 10 times and an inner loop runs 50 times, a statement in the body of an inner loop would run 500 times!
As an example, if you’re working out, you might do several sets of
bench presses with a fixed number of reps in each set. If you did 3 sets
of 15 bench presses each, your workout program might look like this:
Set your set counter to 0.
While your set counter is less than 3,
set your rep counter to 0.
While your rep counter is less than 15,
do a bench press.
Increase your rep counter by 1.
Rest for 2 minutes.
Increase your set counter.
This way of describing the workout program seems tedious. Most of the description is structural: conditions for the loops and increments for the counters. The only “real” activities are the bench press and the resting. As you can see, the bench press is inside the inner rep loop and will be executed 15 times for each complete execution of the inner rep loop. Since the inner rep loop sits inside the outer set loop, it’ll be executed 3 times, giving a grand total of 45 bench presses. Resting, however, is after the inner rep loop but still contained in the outer set loop and will be executed 3 times, totaling 6 minutes of rest.
As with conditionals, writing out loops in English is tedious and imprecise. In the next section, we’ll discuss the tools for writing loops in Java. Because Java was designed with loops as a central tool, we can write loops more succinctly than in English, squeezing a lot of information into a small space. Because we pack so much information into them, loops can look daunting at first. Remember that the syntax we’ll introduce is only the formal Java way of expressing a condition and a list of instructions to execute repeatedly.
5.3. Syntax: Loops in Java
The Java programming language contains three differently named kinds of
loops: while loops, for loops, and do-while loops. All of them
allow you to write code that will be executed repeatedly. In fact, any
program that uses one kind of loop to solve a problem could be
converted to use either of the other two kinds. The three kinds are
provided in Java partly so that it’s easy to code certain typical forms
of repetition and partly because the C language, an ancestor of Java,
contained these three. We’ll begin by describing while loops because
they have the simplest form and then move on to the other two kinds. We’ll
then explain the syntax for nesting together multiple loops and
finally discuss several of the common pitfalls encountered by
programmers when coding loops.
5.3.1. while loops
Superficially, the syntax of a while loop resembles an if statement.
It starts with the keyword while followed by a boolean condition in
parentheses with a block of code surrounded by braces ({ })
afterward. This similarity is not accidental. The only difference
between the two is that the body of the if statement will run a only
single time, while the body of the while loop will run as long as the
condition remains true. Figure 5.1 shows the pattern of
execution for while loops.

true, all of the statements in the body of the loop are executed, and then the condition is checked again. When the check is false, execution skips past the body of the loop.If we assume that the boolean value atDoor says whether or not we
have reached the door and the method walkTowardsDoor() allows us to
take one step closer to the door, we could formulate our example from
the beginning of the previous section as follows.
while(!atDoor) {
atDoor = walkTowardsDoor();
}Here we assume that the walkTowardsDoor() method gives back a
boolean value that is true if we have reached the door and false
otherwise. Unless the walkTowardsDoor() method is able to change the
value of atDoor, the loop will repeat forever, a phenomenon known as
an infinite loop.
while(true) {
System.out.println("Help me!");
}This code gives an example of an infinite loop. If you run this code inside
of a program, it’ll print out an endless succession of Help me!
messages. Be prepared to stop the program by typing Ctrl+C (hold down
the Control key and press C) because it won’t end otherwise. Not
all infinite loops are this obvious. A programmer will not usually use
true as the condition of a loop, but doing so is not always wrong.
Some loops are expected to continue for quite some time with no definite
end. To leave a loop abruptly, you can use the break command.
while(true) {
System.out.println("Help me!");
break;
}This loop will only print out a single Help me! before exiting. A
break command can be used with an if statement to make a loop that
repeats more than once.
int counter = 0;
while(true) {
System.out.print("the loop ");
counter++;
if(counter >= 3)
break;
}
System.out.println("is on fire!");This loop will print out the loop the loop the loop is on fire! Of
course, the break statement unnecessarily complicates the code. We
could have written equivalent code as follows.
int counter = 0;
while(counter < 3) {
System.out.print("the loop ");
counter++;
}
System.out.println("is on fire!");Now, we move on to a more complicated example that can print out the binary representation of a number.
As we discussed in Chapter 1, binary numbers
are the building blocks of every piece of data inside a modern
computer’s memory. Integers are stored in binary. The representation of
floating-point numbers is more complicated, but it also uses 1s and 0s.
Even the char data type and the String values built from them are
fundamentally stored as binary numbers. For this reason, computer
scientists tend to be familiar with the base 2 number system and how to
convert between it and base 10, our usual number system.
In base 10, the number 379 is equal to 3 · 100 + 7 · 10 + 9 · 1 = 3 · 102 + 7 · 101 + 9 · 100. Moving from right to left, the value of each place increases by a factor of 10. A binary number is the same, except that the increase is by a factor of 2 and no single digit is greater than 1. Thus, the number 1010112 = 1 · 25 + 0 · 24 + 1 · 23 + 0 · 22 + 1 · 2 + 1 · 20 = 1 · 32 + 0 · 16 + 1 · 8 + 0 · 4 + 1 · 2 + 1 · 0 = 43. In binary, the number 379 = 1011110112.
To convert a number n to binary, we first find the largest power of 2 that is not larger than n. Then, we begin a repetitive process that stops when the power of 2 under consideration is 0. If 2 raised to the current power is bigger than n, we print out a 0 because that power is too big for n. Otherwise, we print out a 1, subtract 2 raised to that power from n, and move on to the next smaller power of 2. This process will print a 0 for every power of 2 that’s not in n and a 1 for every one that is, giving exactly the definition of a number written in base 2.
import java.util.*;
public class DecimalToBinary {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("Please enter a base 10 number: ");
int number = in.nextInt();
int power = 1;
while(power <= number/2)
power *= 2;
while(power > 0) {
if(power > number)
System.out.print(0);
else {
System.out.print(1);
number -= power;
}
power /= 2;
}
}
}The first while loop in this program doubles the value of power
until doubling it again would make it larger than number. We go up to
and including number/2, otherwise we’d stop when power was
larger than number. After that loop, we begin repeatedly checking to
see if a given power of 2 is bigger than the value left in number. If
it is, we know that we do not use that power. If it’s not, we do and
must remove that power from the value of number.
You may have been tempted to solve this problem by determining if a
given number is even or odd. If it’s even, then you record a 0, and if
it’s odd, then you record a 1. You could then divide the number by two
and repeat the process of determining whether it is even or odd. You
would continue this process until the number became 0. This procedure
requires only a single while loop and would give the digits of the
number in base 2. Unfortunately, you would get the digits in reverse
order. Because we write our numbers with the most significant digit on
the left, we had to use the code given above to first find the largest
value and work backward, in order to determine the binary digits in the
correct sequence.
5.3.2. for loops
Let’s return to our code that prints out
the loop the loop the loop is on fire!
int counter = 0;
while(counter < 3) {
System.out.print("the loop ");
counter++;
}
System.out.println("is on fire!");This code involves some initialization, a condition, and an update, as
many loops do. The initialization sets counter to 0, the condition
checks to make sure that counter is less than 3, and the update
increments counter by 1 every iteration of the loop. These three
elements are so common that a special kind of loop called the for loop
was designed with them explicitly in mind. Most for loops are
dependent on a single counting variable. To make the loop easy to read,
the initialization, condition, and update, all of which relate to this
variable, are pulled into the header of the loop. We could code the
previous while loop example more cleanly, using a for loop, as
follows.
for(int i = 0; i < 3; i++) {
System.out.print("the loop ");
}
System.out.println("is on fire!");The header of a for loop consists of those three parts: the
initialization, the condition, and the update, all separated by
semicolons. Figure 5.2 shows the pattern of execution for
for loops.

true, all of the statements in the body of the loop are executed, followed by the increment step. Then the condition is checked again. When the check is false, execution skips past the body of the loop.You may have noticed that we changed the variable name used within
the loop from counter to i. Doing so doesn’t change the function of
the code. We did so because using the variables i, j, and sometimes
k is a very common practice with for loops. By using variables named
like this, we are indicating that the variable is just a dummy counter
that we are using to make the loop work, not some variable with a
grander purpose. Also, with three uses of a single variable in the
header of a for loop, a long variable name takes up a lot of space.
for loops are used in Java programs more than the other two loops.
They work well when you know how many times you want to iterate through
the loop, which you often do. You can think of the first part of the
for loop header as the starting point, the second part as the ending
point, and the third part as how you get from the start to the end. Many
beginning programmers get stuck on the idea that every for loop starts
with int i = 0 and ends with i++. While this pattern is often true,
there are many other ways to use a for loop. For example, we could print
the powers of 2 that are less than 1000.
for(int i = 1; i < 1000; i *= 2) {
System.out.println(i);
}This segment of code prints out 1, 2, 4, 8, 16, 32, 64,
128, 256, and 512 on separate lines, which are the powers of
2 from 20 up to 29.
Both of the examples of for loops we
have given have only had a single executable line in the body of the
loop. Like if statements, loops only require braces if their bodies
have more than one executable line. Many of the while loops from the
previous subsection could have been written without braces.
Just because a for loop already has a counting mechanism doesn’t mean
that we won’t need other variables to perform useful tasks. For
example, given a String, we could try to find the letter of the
alphabet in the String which is closest to the end of the alphabet.
For the String "Pluto is no longer a planet", the latest letter in
the alphabet is 'u'. To write code that will do this job, we must use
the counting variable from the for loop as an index into the
String. Then, we must also have a temporary variable where we keep the
latest letter found so far. To get the ith char from a
String, we can use the charAt() method. Recall that the index of the first
char in a String is 0, and the index of the last char is one less
than the length of the String.
String s = "The quick brown fox jumps over the lazy dog.";
String lower = s.toLowerCase();
char latest = ' ';
char c;
for(int i = 0; i < lower.length(); i++) {
c = lower.charAt(i);
if(c >= 'a' && c <= 'z' && c > latest)
latest = c;
}
System.out.println("The latest character in the alphabet from your message is: '"
+ latest + "'.");The first thing we do in this example is convert s to lowercase, so
that we are comparing all char values in the same case. Next, we run
through lower, starting at index 0 and going until we reach the end of
the String. For each char, we check to see if it is an alphabetic
character and then if it is later in the alphabet than our current
latest. If it is, we store it into latest. After the loop, we print
out the value in latest. We have chosen the char ' ' because it is
numerically earlier than all the letters in the alphabet. If the output
is a space, we’d know that none of the characters in s were
alphabetic.
For the example given, the latest character in the alphabet is 'z'
because of the word "lazy". One weakness in this code is that it will
always search through the entire String, even if the letter 'z' has
already been found. For the String
"The quick brown fox jumps over the lazy dog.", we’re not wasting too
much time. However, if the String were "Zanzibar!" followed by the
full text of War and Peace, we’d be wasting thousands and
thousands of operations reading characters when we knew that 'z' was
going to be the latest letter, no matter what. We can rewrite our
for loop so that it quits early if it reaches a 'z'.
for(int i = 0; i < lower.length(); i++) {
c = lower.charAt(i);
if(c >= 'a' && c <= 'z' && c > latest)
latest = c;
if(latest == 'z')
break;
}This version of the for loop will break out immediately if the latest
is already a 'z'. This code will work efficiently, but many
professional programmers discourage the use of break except when
absolutely necessary (like in a switch statement). If a break is
used to exit the loop, this logic can be encoded into the condition of
the loop. Thus, the same loop written with better style would be the
following.
for(int i = 0; i < lower.length() && latest != 'z'; i++) {
c = lower.charAt(i);
if(c >= 'a' && c <= 'z' && c > latest)
latest = c;
}For this final version of the loop, we have made the conditional portion
of the header more complex. The comparison using < gives a boolean
that we combine using && with the boolean from the comparison
using !=. As always, remember that the loop will continue iterating as
long as the condition is true. Since we need both parts of the
condition to be true to continue executing, we use the && operator
to connect them.
We apologize to international readers for focusing on the Latin alphabet
used by English and many other Western European languages. It should be
possible to make a localized version of this example with any alphabet
by checking the return value of Character.isLetter(c), which is valid
for all single-character Unicode values, although the idea of
alphabetical order doesn’t really apply to some character systems like
the hanzi and kanji of Chinese and Japanese. Regardless, using the
Character.isLetter() method is recommended for almost all
applications, since it’s more general and more readable.
Prime numbers are integers greater than 1 whose only factors are 1 and themselves. If you’ve encountered prime numbers before, they probably seemed like a mathematical curiosity and nothing more. In fact, prime numbers are the basis of a very practical application of mathematics: cryptography. With the use of some math and very large prime numbers, computer scientists have devised techniques that make messages sent over the Internet more secure.
These techniques are beyond the scope of this book, but we can at least write some code to determine if a number n is prime. To do so, we can simply divide n by all the numbers between 2 and n - 1. If none of the numbers divide it evenly, it must be prime. Here is this basic solution.
import java.util.*;
public class PrimalityTester0 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("Please enter a number: ");
long number = in.nextLong();
boolean prime = true;
for(long i = 2; i < number && prime; i++)
if(number % i == 0)
prime = false;
if(prime)
System.out.println(number + " is prime.");
else
System.out.println(number + " is not prime.");
}
}This program has a for loop that runs from 2 up to number - 1,
provided that we don’t find a number that evenly divides number. This
optimization means that the program will output the moment that it knows
that the number is not prime, but we’ll have to wait for it to
check all the other possibilities before it is sure that the number is
prime.
One insight that we can use to make the program more efficient is that, after checking 2, we don’t have to divide it by any even numbers. So, we can do half the checking with a few simple modifications.
import java.util.*;
public class PrimalityTester1 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("Please enter a number: ");
long number = in.nextLong();
boolean prime = number == 2 || number % 2 != 0;
for(long i = 3; i < number && prime; i += 2 )
if(number % i == 0)
prime = false;
if(prime)
System.out.println(number + " is prime.");
else
System.out.println(number + " is not prime.");
}
}This version of the program sets the boolean variable prime to
false if number is divisible by 2 (unless it’s 2 itself) and true otherwise. Then, it
starts the search at 3 and continues in jumps of 2. Although we save half the checks,
we can do much better. Note that if a number n is divisible by 2, then it’s also divisible by
n/2. So, if a number is not divisible by 2, it’s also not divisible by any
number larger than n/2. If it’s not divisible by 2 or 3, then it’s also not divisible by any number
larger than n/3. If it’s not divisible by 2 or 3
or 4, it’s not divisible by any number larger than
n/4, and so on. Thus, we don’t have to check all
the way up to n - 1. If we’re checking to see if
n is divisible by x and learning that
n is not divisible by anything larger than
n/x, the point where x = n/x
is as follows.

Thus, we only need to search up to the square root of n, which will save much more time.
import java.util.*;
public class PrimalityTester2 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("Please enter a number: ");
long number = in.nextLong();
boolean prime = number == 2 || number % 2 != 0;
long root = (long)Math.sqrt(number);
for(long i = 3; i <= root && prime; i += 2 )
if(number % i == 0)
prime = false;
if(prime)
System.out.println(number + " is prime.");
else
System.out.println(number + " is not prime.");
}
}Note in this version of the program we do go up to and including root,
because there’s the possibility that number is a perfect square.
DNA is usually double stranded, with each base paired to another specific base, called its complementary base. The following table shows the association between each base and its complementary base.
| Base | Abbreviation | Complementary Base |
|---|---|---|
Adenine |
A |
T |
Cytosine |
C |
G |
Guanine |
G |
C |
Thymine |
T |
A |
A simple but common task is finding the reverse complement of a DNA sequence. The reverse complement of a DNA sequence is its sequence of complementary bases given in reverse order. For example, the reverse complement of ACATGAG is CTCATGT. This sequence is found by first finding the complement of ACATGAG, which is TGTACTC, and then reversing its order.
We’ll write a program that finds the reverse complement of a DNA
sequence entered by a user. This sequence will be entered as a sequence
of characters made up of the four abbreviations for the bases: A, C, G,
and T. We’ll store this sequence as a String and perform some
manipulations on it to get the reverse complement.
import java.util.*;
public class ReverseComplement {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("Please enter a DNA sequence: ");
String sequence = in.next().toUpperCase();
String complement = "";
for(int i = 0; i < sequence.length(); i++) (1)
switch(sequence.charAt(i)) { //get complements
case 'A': complement += "T"; break;
case 'C': complement += "G"; break;
case 'G': complement += "C"; break;
case 'T': complement += "A"; break;
}
String reverseComplement = "";
//reverse the complement
for(int i = complement.length() - 1; i >= 0; i--) (2)
reverseComplement += complement.charAt(i);
System.out.println("Reverse complement: " + reverseComplement);
}
}| 1 | This example first creates a String filled with the complement of the
base pairs from the input String. |
| 2 | Then, it creates a
new String that is the reverse of the complement sequence. |
Note how
complement is created by appending the char corresponding to the
complementary base at the end of complement. If we inserted each
char at the beginning of complement, we wouldn’t need to reverse in
a separate step.
import java.util.*;
public class CleverReverseComplement {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("Please enter a DNA sequence: ");
String sequence = in.next().toUpperCase();
String reverseComplement = "";
for(int i = 0; i < sequence.length(); i++)
switch(sequence.charAt(i)) { //get complements
case 'A': reverseComplement = "T" + reverseComplement; break;
case 'C': reverseComplement = "G" + reverseComplement; break;
case 'G': reverseComplement = "C" + reverseComplement; break;
case 'T': reverseComplement = "A" + reverseComplement; break;
}
System.out.println("Reverse complement: " + reverseComplement);
}
}5.3.3. do-while loops
Use this rule of thumb for deciding which kind of loop to use: If you
know how many times you want the loop to execute, use a for loop. If
you don’t know how many times you want it to execute, use a while
loop. Clearly, this rule is not iron-clad. In the previous example, we
used a for loop even though it would stop executing as soon as a 'z'
was encountered. Nevertheless, it seems like we have covered all of the
possible situations with while and for loops. When should we use
do-while loops? The simple answer is: never.
You never have to use a do-while loop. With a little bit of effort,
you could use a single kind of loop for every job. The key difference between
a do-while loop and a regular while loop is that a do-while loop
will always run at least once. Neither of the other two loops give you
that guarantee. The syntax for a do-while loop is a do at the top of
a loop body enclosed in braces, with a normal while header at the end,
including a condition in parentheses, followed by a semicolon.
Figure 5.3 shows the pattern of execution for do-while
loops.

false, execution skips past the body of the loop. A do-while loop is guaranteed to run at least once.We can use a do-while loop to print out the first 10 perfect squares
as follows.
int x = 1;
do {
System.out.println(x*x);
x++;
} while(x <= 10);This loop behaves exactly the same as the following loop.
int x = 1;
while(x <= 10) {
System.out.println(x*x);
x++;
}The time when a do-while loop is really going to shine is when your
program will work incorrectly if the loop doesn’t run at least once.
This situation often occurs with input, when the loop must run at least
once before checking the condition. For example, imagine that you want
to write a program that picks a random number between 1 and 100 and lets
the user guess what it is until the user gets it right. You need a loop
because it’s a repetitive activity, but you need to let the user guess
at least once so that you can check if he or she was right. The
following program fragment does exactly that.
Scanner in = new Scanner(System.in);
Random random = new Random();
int guess;
int number = random.nextInt(100) + 1;
do {
System.out.print("What's your guess? ");
guess = in.nextInt();
} while(guess != number);
System.out.println("You got it! The number was " + number + ".");You could perform the same function with a while loop, but you’d
need to get input from the user before the loop starts. Using the
do-while loop is a little more elegant.
5.3.4. Nested loops
Just as you can nest if statements, it’s possible to nest loops inside of other
loops. In the simplest case, you may have some repetitive activity that
itself needs to be performed several times. For example, when you were
younger, you probably had to learn your multiplication tables. For each
number, a multiplication table gave the value of the product of that
number by every integer between 1 and 12. We can write code to print out
out the multiplication table for every number from 1 to 10 by simply
repeating the process.
for(int number = 1; number <= 10; number++) {
for(int factor = 1; factor <= 12; factor++) {
System.out.println(number + " x " + factor +
" = " + number*factor);
}
System.out.println();
}The outer loop incrementing number runs 10 times. The inner loop
incrementing factor will run 12 times for each iteration of the outer
loop. Thus, the code in the inner loop will run a total of 120 times.
Every 12 iterations, the inner loop will stop, and an extra blank line
will be added by the System.out.println() method in the outer loop.
The sequence consisting of 1, 3, 6, 10, 15, and so on is known as the triangular numbers. The ith triangular number is the sum of the first i integers. They are called triangular numbers because they can be drawn as equilateral triangles in a very natural way, if you use a number of dots equal to the number.
We can use nested loops to print out the first n triangular numbers, where n is specified by the user.
import java.util.*;
public class TriangularNumbers {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("How many triangular numbers? ");
int n = in.nextInt();
int sum;
for(int i = 1; i <= n; i++) {
sum = 0;
for(int j = 1; j <= i; j++)
sum += j;
System.out.println(sum);
}
}
}As you can see, the outer loop iterates through each of the n
different triangular numbers. Then, the inner loop does the summation
needed to compute the given triangular number. However, producing a sequence of
triangular numbers this way is inefficient. Nested loops are an effective way to solve many problems,
particularly certain types of problems using arrays, but we can generate
triangular numbers using only a single for loop. The key insight is
that we can keep track of the previous triangular number and add
i to it, as i increases.
import java.util.*;
public class CleverTriangularNumbers {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("How many triangular numbers? ");
int n = in.nextInt();
int triangular = 0;
for(int i = 1; i <= n; i++) {
triangular += i;
System.out.println(triangular);
}
}
}By removing the inner for loop, the total amount of work needed is
greatly reduced.
5.3.5. Common pitfalls
With great power comes great responsibility. The power to repeat things a large number of times means that we can also repeat our mistakes a large number of times. Many classic bugs occur as a result of logical or typographical errors in loops. We list a few of the most common below.
|
Pitfall: Infinite loops
It’s possible to create a loop that never terminates. Your program may take a long time to finish, but if it takes much longer than you expect, an infinite loop might be the culprit. Infinite loops might occur because you forgot to include an appropriate statement to advance a counter. This code is presumably intended to print out the first 100 integers,
but there’s no code that increases the value of One might expect this code to print out 20 lines of output. However,
remember that |
|
Pitfall: Almost infinite loops
Many loops are truly infinite; others take a really long time. For example, if you intended to run a loop down from 10 to 0, but increment your counter instead of decrementing it, overflow means that you will eventually get to a number less than 0, but it will take more than 2 billion increments instead of the expected 10 decrements. This loop will significantly slow your code. Everyone will be so tired of waiting that they might leave the rocket launch. Of course, another problem with almost infinite loops is that you are dealing with the wrong values. No one expects to hear the number 2,147,483,647 in a countdown. |
|
Pitfall: Fencepost errors
Perhaps the most common loop errors are fencepost errors, often known as off-by-one errors. The name “fencepost” comes from a related mistake that someone might make when putting up a fence. Imagine that you want to erect a 10 meter long chain link fence with a support post every meter, how many posts do you need? In fact, we haven’t given you enough information to answer the question correctly. If your fence is built in a straight line, you’ll need 11 posts so that you have a post at each end. However, if your fence is a rectangular enclosure, say 3 meters by 2 meters, you’ll only need 10 posts. In loops, fencepost errors are often due to zero-based counting. A Of course, sometimes we need one-based counting instead. After being used to zero-based counting, a programmer might make the following loop that incorrectly iterates 9 times. The correct version that iterates 10 times is below. If you want to iterate n times, start at 0 and go up to
but not including n or alternately start at 1 and go up to and
including n. To keep loop headers consistent, some
programmers always start at 0 and then adjust the values inside the
loop, printing out |
|
Pitfall: Skipped loops
A loop runs as long as its condition is For example, we can write a program that will add any number of positive values. When the user is finished using the adder, he or she enters a negative number. This negative number, called a sentinel value, tells the program to stop executing the loop. Below is an incorrect implementation of such a program. This loop will never be executed because |
|
Pitfall: Misplaced semicolons
The idea of a statement in Java is often amorphous in the minds of beginning programmers. An entire loop (with any number of loops nested inside of it) is considered one statement. An executable statement ending with a semicolon is one statement as well, even when that executable statement is empty. Thus, the following is a legal (but infinite) loop. This code was supposed to count down from 100, just like in the game of
Hide and Seek; however, there is a semicolon after the condition of the
This error is common especially for those new to loops and conditional
statements and are in the habit of putting semicolons after everything.
A misplaced semicolon doesn’t always result in an infinite loop. Here
is the This version of the code will execute similarly, except the decrement is
built into the header of the loop. So, the loop will execute the empty
statement, but it will also decrement There are some cases when an empty statement for a loop body is useful although it is never necessary. In future chapters, we’ll point out situations in which you may wish to use an empty statement this way. |
5.4. Solution: DNA searching
Below we give a solution to the DNA searching problem posed at the
beginning of the second half of this chapter. Our solution prints out
the index within the sequence when it finds a match with the
subsequence it’s looking for. Afterward, it prints out the total number of
matches. Our code also does error checking to make sure that the user
only enters valid DNA sequences containing the letters A, C, G, and T.
We begin our code with the standard import statement and class
definition.
import java.util.*;
public class DNASearch {
public static void main(String[] args) {
Scanner in = new Scanner(System.in); (1)
String sequence, subsequence;
boolean valid; (2)
char c;| 1 | The main() method instantiates a Scanner object and declares both of
the String variables we’ll need to store the DNA sequences. |
| 2 | The method
also declares a boolean and a char we’ll use for input checking. |
do {
System.out.print("Enter the DNA sequence you wish to search in: "); (1)
sequence = in.next().toUpperCase(); (2)
valid = true;
for(int i = 0; i < sequence.length() && valid; i++) { (3)
c = sequence.charAt(i);
if(c != 'A' && c != 'C' && c != 'G' && c != 'T') { (4)
System.out.println("Invalid DNA sequence!");
valid = false;
}
}
} while(!valid); (5)| 1 | Next, the user is prompted for a DNA sequence to search in. |
| 2 | This
String stored in sequence is converted to uppercase just in case
the user is not being consistent. |
| 3 | The inner for loop in this code checks each char inside of sequence. |
| 4 | If any char is not an
'A', 'C', 'G', or 'T', then valid is set to false. As a
result, the for loop terminates. Also, the do-while loop repeats the
prompt and gets a new String for sequence from the user. |
| 5 | This outer
do-while loop continues as long as the user keeps entering invalid DNA
sequences. |
do {
System.out.print("Enter the subsequence you wish to search for: ");
subsequence = in.next().toUpperCase();
valid = true;
for(int i = 0; i < subsequence.length() && valid; i++) {
c = subsequence.charAt(i);
if(c != 'A' && c != 'C' && c != 'G' && c != 'T') {
System.out.println("Invalid DNA sequence!");
valid = false;
}
}
} while(!valid);The code used to input subsequence while doing error checking is
virtually identical to the code to input sequence.
int found = 0;
for(int i = 0; i < sequence.length() - subsequence.length() + 1; i++) { (1)
for(int j = 0; j < subsequence.length(); j++) { (2)
if(subsequence.charAt(j) != sequence.charAt(i + j)) (3)
break;
if(j == subsequence.length() - 1) { //matches (4)
System.out.println("Match found at index " + i);
found++;
}
}
}| 1 | The workhorse of the search is found in these nested for loops.
The outer loop iterates through every index in sequence, until it
comes to an index that is too late to be the start of a new subsequence
(since the subsequence would be too long to fit anymore). This happens
to be when the value of i is greater than or equal to
sequence.length() - subsequence.length() + 1. It may take some thought
to verify that this condition is the correct one. One way to think about
this problem is by noting that, when sequence and subsequence have
the same length, you need to check starting at index 0 of sequence
but not any later indexes. Also, if subsequence is one char longer
than sequence, there can never be a match. In that case, the value of
sequence.length() - subsequence.length() + 1 would be 0. Since 0
is not less than 0, the outer for loop would never execute. |
| 2 | The inner for loop iterates through the length of subsequence,
making sure that every char in sequence, starting at the appropriate
offset, exactly matches a char in subsequence. |
| 3 | If, at any point, the
two char values do not match, the inner for loop will immediately
exit, using the break command. |
| 4 | However, on the last iteration of the
inner for loop, when j is one less than the length of subsequence,
we know that all of subsequence matched a part of sequence. As a
result, we print out the index of sequence where subsequence started
and increment the found counter. |
If you know the String class well, you can use the indexOf() method
to replace the inner for loop. We leave that approach as an exercise.
Finally, we print out the total number of matches found. In order to
avoid awkward output like 1 matches found., we used an if-else to
customize the output based on the value of found.
if(found == 1)
System.out.println("One match found.");
else
System.out.println(found + " matches found.");
}
}The ideas needed to correctly implement the solution are not difficult, but catching all the off-by-one errors and getting every detail right takes care. There’s also more than one way to code this solution. For example, we could have written the nested loops that do the searching as follows.
int found = 0;
for(int i = 0; i < sequence.length() - subsequence.length() + 1; i++) {
for(int j = 0; j < subsequence.length() &&
subsequence.charAt(j) == sequence.charAt(i + j); j++)
if(j == subsequence.length() - 1) { // Matches
System.out.println("Match found at index " + i);
found++;
}
}
}This design is preferred by many since it removes the break. By using
an empty statement, it’s possible to move the check to see if the
matching process is done outside of the inner for loop.
int found = 0;
int j;
for(int i = 0; i < sequence.length() - subsequence.length() + 1; i++) {
for(j = 0; j < subsequence.length() &&
subsequence.charAt(j) == sequence.charAt(i + j); j++);
if(j == subsequence.length()) { // Matches
System.out.println("Match found at index " + i);
found++;
}
}In this case, note that we must declare j outside of the inner for
loop, since it will be used outside. This approach is more efficient
because we only need to perform the check once. Note that the
condition of the if statement has also changed. Now, we know that all of
subsequence matches because the loop ran to completion. If the loop
did not run to completion, then j would be smaller than
subsequence.length() and the loop must have terminated because the two
char values did not match. Although more efficient, some programmers
would avoid this approach because it uses confusing syntax in which
the body of the for loop is a single empty statement followed by a
semicolon. Likewise, the logic about exiting the loop and the condition
of the if statement is murkier.
5.5. Concurrency: Loops
Many programmers use concurrency for speedup, to make their programs to run faster. Most programs that run for a long time use loops to do repetitive tasks. If these loops are doing the same operation to many different pieces of data, we may be able to speed up the process by splitting up the data and letting different threads operate on their own segment of the data. Splitting up data this way is called domain decomposition which allows us to achieve data parallelism. These topics are discussed further in Section 13.3.
Performing repetitive tasks is one of the great strengths of computers. For most programs that run a long time, incredible amounts of computation are being done inside of (usually nested) loops. Domain decomposition will not work for all of these programs. Some cannot be parallelized at all, but this book is about finding problems that can have parallel and concurrent solutions.
In Chapter 13, we’ll introduce tools for writing a concurrent program with different threads of execution running at the exactly the same time and potentially interacting. Using only the power of loops, you can see parallelism in action now.
Consider the problem of computing the sum of the sines of a range of integers. At its heart is a loop from the start of the range to the end.
for(int i = start; i <= end; i++)
sum += Math.sin(start);If we want to allow the user to specify the start and the end and print out the sum, we need to make a program with a little bit of input and output around this loop.
import java.util.Scanner;
public class SumSines {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("Enter starting value: ");
int start = in.nextInt();
System.out.print("Enter ending value: ");
int end = in.nextInt();
double sum = 0;
for(int i = start; i <= end; i++)
sum += Math.sin(start);
System.out.println("Sum of sines: " + sum);
}
}If you compile and run this program with 1 as the start value and
100000000 as the end, the answer should be 1.7136493465700542. One
hundred million values is a lot to find the sine for. Depending on your
machine, this task should take between 10 seconds and over a minute. Try
to time how long this takes as accurately as possible.
Now, open a total of four terminal windows and navigate them all to the
directory with SumSines.class in it. Run SumSines in each one. For
the first terminal, enter 1 as the start and 25000000 as the end. For
the second, enter 25000001 and 50000000. For the third, enter
50000001 and 75000000. For the last, enter 75000000 and
100000000. Once they have run, you should get, respectively,
1.4912473269134603, -0.6795491754132104, -0.2893142602684644, and
1.1912654553381272. If you add these together using a calculator, you
should get 1.7136493465699127, which is almost exactly the same answer
we got before. (Floating-point rounding errors cause the slight
difference.)
If you try to start them computing at about the same time, you can try to see how long it takes for all of them to complete. Did it take less time than before? If you have a single core processor, it might have taken just as long or longer. If you have a dual-core processor, it should have taken less time, and if you have a quad core processor, even less. Since we’re dividing the problem into four pieces, we don’t expect to see any improvement with more than four cores.
Most operating systems provide a graphical way of viewing the load on each processor. If you examine your CPU usage while running those programs, you should see it spike up when the programs start and then come down when they finish. For multiple cores, how did we say which core we wanted each program to run on? We didn’t. In general, it’s difficult to specify which core we want to run a program, process, or thread on. The OS does the job of scheduling and picks a free processor when it needs to run a program. It’s even possible for programs and threads to change from one core to another while running if the OS needs to balance out the workload.
This sines example is similar to Example 13.10 in Chapter 13. As you may have noticed, running four programs simultaneously is not convenient. You have to open several windows, you have to type starting and ending points very carefully, and you have to combine the answers at the end since your programs cannot interact directly with each other. Features of Java will make this job easier, allowing us to run more than one thread of execution at a time without the need to run multiple programs by hand.
5.6. Exercises
Conceptual Problems
-
If you have a
Stringcontaining a long text and you want to count the number of words in the text that begin with the letter'm', which of the three kinds of loops would you use, and why? -
In Example 5.2, our last version of the primality tester
PrimalityTester2computes the square root of the number being tested. Instead of computing this value before the loop, how would performance be affected by changing the head of theforloop to the following?for(long i = 3; i <= Math.sqrt(number) && prime; i += 2) -
How many different DNA sequences of length n are there?
-
There are three different errors in the following loop intended to print out the numbers 1 through 10. What are they?
for(int i = 1; i < 10; i--); { System.out.println(i); } -
Consider the following code containing nested
forloops.Scanner in = new Scanner(System.in); int n = in.nextInt(); int count = 0; for(int i = 1; i <= n; i++) for(int j = 1; j <= i; j++) count++;In terms of the value of
n, how many times iscountincremented? If it’s not immediately obvious, trace through the execution of the program by hand or run the code for several different values ofnand try to detect a pattern.
Programming Practice
-
Write a program that converts base 10 numbers into base 3 numbers. If you find that task too easy, write a program that will convert base 10 numbers to any base in the range 2 to 16. Hint: Use letters A through Z, in order, to represent digits larger than 9.
-
The greatest common divisor (GCD) of two integers is the largest integer that divides both of them evenly. The GCD for any two positive integers is at least 1 and at most the smaller of the two numbers. Write a program that prompts a user for two
intvalues and finds their GCD. Although there are more efficient methods, you can count down from either number. If the counter ever divides both numbers evenly, it’s the GCD. The counter is guaranteed to divide them both if it reaches 1. -
In the solution to the DNA searching problem given in Section 5.4, we used two
forloops to find occurrences of a DNA subsequence inside of a larger sequence. Professional Java developers would have used a singleforloop and theindexOf()method in theStringclass. One version of this method returns the index of a substring within aStringobject, starting from a particular offset, as shown below.String text = "fun dysfunction"; String search = "fun"; System.out.println("Location: " + text.indexOf(search, 4));This code will output
Location: 7since the first occurrence of"fun"from index4or later starts at index7. If there are no more occurrences of the substring beyond the starting index, the method will return-1. Rewrite the solution to the DNA searching problem, replacing the inner searchingforloop with theindexOf()method. -
Write a program that reads a number n from a user and then prints all possible DNA sequences of length n. Be careful not to supply too large of a value when you run this program. Hint: Represent the sequence as a
String. On each iteration, focus on the lastcharin theString. If it is an'A', change it to a'C'. If it is a'C', change it to a'G'. If it is a'G', change it to a'T'. If it is a'T', change it back to an'A', but “carry” the increment over to the nextchar, like a rolling odometer. You will have to design loops that can deal with carries that cascade across multiple indexes. -
Re-implement the solution to the DNA searching program given in Section 5.4 using
JOptionPaneto generate GUIs for input and output.
Experiments
-
Using a
forloop, record the Monty Hall simulation so that you can run it 100 times, always choosing to switch doors. Keep a record of how many times you win. Change your code again to run the Monty Hall simulation 100 more times, always choosing to keep your initial choice. Again, keep a record of how many times you win. Compare the two records. Choosing to switch should perform roughly twice as well as sticking with your initial choice. Increase the number of iterations to 1,000 and then 10,000 times. Does the performance of switching get closer to twice the performance of not switching? -
Write three nested
forloops, each of which run 1,000 times. Increment a counter in the innermostforloop. If that counter starts at 0, its final value should be 1,000,000,000. Time how long your program takes to run to completion using either a stopwatch or, if you’re on a Unix or Linux system, thetimecommand. Feel free to increase and decrease the amount that each loop runs to see the effect on the time. However, if you increase the values of all three loops too much, you may have to wait a long while. -
In Section 5.3.5, one of the common loop mistakes we discuss is an almost infinite loop. Create your own almost infinite loop that runs from
10to0, incrementing instead of decrementing. Time the execution of your program. Unlike our example, do not use an output statement or your code will take too long to run. How much longer would your code take to run if you used alonginstead of anint? -
In Example 5.2, we gave three programs to test a number for primality. Run each of these prime testers on a large prime such as 982,451,653 and time them. Is there a significant difference in the running time of
PrimalityTester0andPrimalityTester1? What aboutPrimalityTester1andPrimalityTester2? -
In Example 5.5, we ran four programs at the same time to solve a problem in parallel. Use the same framework (combined with your knowledge of primes from Example 5.2) to write a program that can see how many prime numbers are in a user specified range of integers. Then, use it to find the total number of primes between 2 and 500,000,000. Now, run two copies of the program with one starting at 2 and going up to 250,000,000 and the other starting at 250,000,001 and going up to 500,000,000. If you add the numbers together, do you get the same answer? (If not, there is a bug in your program.) Now, divide the work into four pieces. How much quicker, if at all, is running all four programs instead of one? Does one of the four pieces run significantly faster or slower than the others?
6. Arrays
Too much of a good thing can be wonderful.
6.1. Introduction
With one exception, all of the types we’ve talked about in this book
have held a single value. For example, an int variable can only
contain a single int value. If you try to put a second int value
into a variable, it will overwrite the first.
The String type, of course, is the exception. String objects can
contain char sequences of any length from 0 up to a practically
limitless size (the theoretical maximum length of a Java String is
Integer.MAX_INT, more than 650 times the length of War and Peace).
As remarkable as String objects are, this chapter is about a more
general kind of list called an array. We can create arrays to hold a
list of any type of variable in Java.
The ability to work with lists expands the scope of problems that we can solve. Beyond simple lists, we can use the same tools to create tables, grids, and other structures to solve fascinating problems like the one that comes next.
6.2. Problem: Game of Life
Some physicists insist that the rules governing the universe are horribly complicated. Some insist that the fundamental laws are simple and only their overall interaction is complex. With the power to do simulations quickly, computer scientists have shown that some systems can exhibit very complex interactions using simple rules. Perhaps the best known examples of these systems are cellular automata, of which Conway’s Game of Life is the most famous.
The framework for Conway’s Game of Life is an infinite grid made up of squares called cells. Some cells in the grid are black (or alive, to give it a biological flavor), and the rest are white (or dead). Any given cell has 8 neighbors as shown in the figure below.

The pattern of alive and dead cells at any given time on the grid is called a generation. To determine the next generation, we use the following rules.
-
If a living cell has fewer than two living neighbors, it dies from loneliness.
-
If a living cell has more than three neighbors, it dies because of overcrowding.
-
If a living cell has exactly two or three living neighbors, it lives to the next generation.
-
If a dead cell has exactly three live neighbors, it becomes a living cell.
These four simple rules allow for more complex interactions than you might expect. The patterns that emerge from applying these rules to a starting configuration of alive and dead cells strike a balance between complete chaos and rigid order. As the name of the game implies, the similarity to biological patterns of development can be surprising.
Your problem is to create a Life simulator of size n × m, specific values for which will be discussed below. The program should simulate the process at a speed that is engaging to watch, with a new generation every tenth of a second. The program should begin by randomly making 10% of all the cells living and the rest dead.
6.2.1. Terminal limitations
One problem you might be worrying about is how to display the
simulation. In Chapter 15 you’ll learn how to make a graphical user interface (GUI)
that can display a grid of cells in black and white and much more
interesting things as well. For now, the main tool that we can use for
output is still the terminal. The output method we recommend is printing
an asterisk ('*') for a living cell and a space (' ') for a dead
one. In this way you can easily see the patterns form on the screen and
change over time.
The classic terminal isn’t very big. For this reason, we suggest that you set the height of your simulation to 24 rows and the width of your simulation to 80 columns. These dimensions conform to the most ancient terminal sizes. If your terminal screen is much larger, you can change the width and height later to perform a larger simulation. No matter how large the display for the game is, the ideal size of the game. Because our size is so limited, we must deal with the problem of a cell on the boundary. Anything beyond the boundaries should be counted as dead. Thus, a cell right on the edge of the simulation grid can have a maximum of 5 neighbors. A cell in one of the four corners can only have 3 neighbors.
In order to give the appearance of smooth transitions, you need to print out each new generation of cells quickly, and in the same locations as the previous generation. Simply printing one set after another will not achieve this effect unless your terminal screen is exactly 24 rows tall. So, you will need to clear the screen each time. In an effort to be platform independent, Java does not provide an easy way to clear the terminal screen. A quick and simple hack is to simply print out 100 blank lines before printing the next generation. This hack will work as long as your terminal is not significantly more than 100 rows in height. If it is, you’ll need to print a larger number of blank rows.
Finally, you need to wait a short period of time between generations so that the user can see each configuration before it’s cleared away and replaced by the next one. The simplest way to do this is by having your program go to sleep for a short period of time, a tenth of a second as we suggested before. The code to make your program sleep for that amount of time is:
try { Thread.sleep(100); }
catch(InterruptedException e) {}We’ll explain this code in much greater detail in Chapter 13.
The key item of importance is the number passed into the sleep() method.
This value is the number of milliseconds you want your program to sleep.
100 milliseconds is, of course, one tenth of a second.
In order to simulate the Game of Life, we need to store information, namely the liveness or deadness of cells, in a grid. First, we need to discuss the simpler task of storing data in a list.
6.3. Concepts: Lists of data
Lists of data are of paramount importance in many different areas of life: shopping lists, packing lists, lists of employees working at a company, address books, top ten lists, and more. Lists are even more important in programming. As you know, one of the great strengths of computers is their speed. If we have a long list of data, we can use that speed to perform operations on all the data quickly. E-mail contact lists, entries in a database, and cells in a spreadsheet are just a few of the most obvious ways that lists come up in computer applications.
Even in Java, there are many different ways to record a list of information, but a list is only one form of data structure. As the name implies, a data structure is a way to organize data, whether in a list, in a tree, in sorted order, in some kind of hierarchy, or in any other way that might be useful. We’ll only talk about the array data structure in this chapter, but other data structures will be discussed in Chapter 18. Below, we give a short explanation of some of the attributes any given data structure might have.
6.3.1. Data structure attribute
- Contents
-
Keeping only a single value in a data structure defeats the purpose of a data structure. But, if we can store more than a single value, must all of those values come from the same type? If a data structure can hold several different types of data, we call it heterogeneous, but if it can only hold one type, we call it homogeneous.
- Size
-
The size of a data structure may be something that’s fixed when it’s created or it could change on the fly. If a data structure’s size or length can change, we call it a dynamic data structure. If the data structure has a size or length that can never change after it’s been created, we call it a static data structure.
- Element Access
-
One of the reasons there are so many different data structures is that different ways of structuring data are better or worse for a given task. For example, if your task is to add a list of numbers, then you’re expecting to access every single element in the list. However, if you’re searching for a word in a dictionary, you don’t want to check every dictionary entry to find it.
Some data structures are optimized so that you can efficiently read, insert, or delete only a single item, often the first (or last) item in the data structure. Some data structures only allow you to move through the structure sequentially, one item after another. Such a data structure has what is called sequential access. Still others allow you to jump randomly to any point you want inside the data structure efficiently. These data structures have what is called random access. Advanced programmers take into account many different factors before deciding which data structure is best suited to their problem.
6.3.2. Characteristics of an array
Now that we’ve defined these attributes, we can say that an array is a
homogeneous, static data structure with random access. An array is
homogeneous because it can only hold a list of a single type of data,
such as int, double, or String. An array is static because it has
a fixed length that is set only when the array is instantiated. An array
also has random access because jumping to any element in the array is
fast and takes about the same amount of time as jumping to any
other.
An array is a list of a specific type of elements that has length n, a length specified when the array is created. Each of the n elements is indexed using a number between 0 and n - 1]. Once again, zero-based counting rears its ugly head. Consider the following list of items: {9, 4, 2, 1, 6, 8, 3}
If this list is stored in an array, the first element, 9, would have index 0, 4 would have index 1, and so on, finishing at 3 with an index of 6, although the total number of items is 7. Not all languages use zero-based counting for array indexes, but many do, including C, C++, and Java. The reason that languages like C originally used zero-based counting for indexes is that the variable corresponding to the array is an address inside the computer’s memory giving the first element in the array. Thus, an index of 0 is 0 times the size of an element added to the starting address, and an index of 5 is 5 times the size of an element added to the starting address. So, zero-based indexes gave a quick way for the program to compute where in memory a given element of an array is.
6.4. Syntax: Arrays in Java
The idea of a list is not mysterious. Numbering each element of the list is natural, even though the numbers start at 0 instead of 1. Nevertheless, arrays are the source of many errors that cause Java programs to crash. Below, we explain the basics of creating arrays, indexing into arrays, and using arrays with loops. Then, there’s an extra subsection explaining how to send data from a file to a program as if the file were being typed in by a user. Using this technique can save a lot of time when you’re experimenting with arrays.
6.4.1. Array declaration and instantiation
To create an array, you usually need to create an array variable first.
Remember that an array is a homogeneous data structure, meaning that it
can only store elements of a single type. When you create an array
variable, you have to specify what that type is. To declare an array
variable, you use the type it’s going to hold, followed by square
brackets ([]), followed by the name of the variable. For example, if
you want to create an array called numbers that can hold integers, you
would type the following.
int[] numbers;If you have some C or C++ programming experience, you might be used to the brackets being on the other side of the variable, like so.
int numbers[];In Java, both declarations are perfectly legal and equivalent. However,
the first declaration is preferred from a stylistic perspective. It
follows the pattern of using the type (an array of int values in this
case) followed by the variable name as the syntax for a declaration.
As we said, arrays are also static data structures, meaning that their
length is fixed at the time of their creation. Yet we didn’t specify a
length above. This declaration has not yet created an array, just a
variable that can point at an array. In the second half of this chapter,
we will further discuss this difference between the way an array is
created and the way an int or any other variable of primitive type is
created. To actually create the array, we need to use another step,
involving the keyword new. Here’s how we instantiate an array of
int type with 10 elements.
numbers = new int[10];We use the keyword new, followed by the type of element, followed by
the number of elements the array can hold in square brackets. This new
array is stored into numbers. In other words, the variable numbers
is now a name for the array. Commonly, the two steps of declaring and
instantiating an array will be combined into one line of code.
int[] numbers = new int[10];It’s always possible to separate the two steps. In some cases, a single variable might be used to point at an array of one particular length, then changed to point at an array of another length, and so on, as below.
int[] numbers;
numbers = new int[10];
numbers = new int[100];
numbers = new int[1000];Here, the variable numbers starts off pointing at no array. Next, it’s
made to point at a new array with 10 elements. Then, it’s made to
point at a new array with 100 elements, ignoring the 10 element array.
Finally, it’s made to point at an array with 1,000 elements, ignoring
the 100 element array. Remember, the arrays themselves are static; their
lengths can’t change. The array type variables, however, can point at
different arrays with different lengths, provided that they’re still
the right type (in this case, arrays of int values).
What values are inside the array when it’s first created? Let’s return
to the case where numbers points at a new array with 10 elements. Each
of those elements contains the int value 0, as shown below.

Whenever an array is instantiated, each of its n elements
is set to some default value. For int, long, short, and byte
this value is 0. For double and float, this value is 0.0. For
char, this value is '\0', a special unprintable character. For
boolean, this value is false. For String or any other reference
type, this value is null, a special value that means there’s no
object.
It’s also possible to use a list to initialize an array. For example,
we can create an array of type double that contains the values 0.5,
1.0, 1.5, 2.0, and 2.5 using the following code.
double[] increments = {0.5, 1.0, 1.5, 2.0, 2.5};This line of code is equivalent to using the new keyword to create a
double array with 5 elements and then setting each to the values
shown.
6.4.2. Indexing into arrays
To use a value in an array, you must index into the array, using the
square brackets once again. Returning to the example of the int array
numbers with length 10, we can read the value at index 4 from the
array and print it out.
System.out.println(numbers[4]);Until some other value has been stored there, the value of numbers[4] is 0,
and so 0 is all that will be printed out.
We can set the value at numbers[4] to 17 as follows.
numbers[4] = 17;Then, if we try to print out numbers[4], 17 will be printed. The
contents of the numbers array will look like this.

The key thing to understand about indexing into an array is that it
gives you an element of the specified type. In other words, numbers[4]
is an int variable in every possible sense. You can read its value.
You can change its value. You can pass it into a method. It can be used
anywhere a normal int can be used, as in the following example.
int x = numbers[4];
double y = Math.sqrt(numbers[2]) + numbers[4];
numbers[9] = (int)(y*x);Executing this code will store 17 into x and 17.0 into y. Then,
the product of those two, 289, will be stored into numbers[9].
Remember, in Java, the type on the left and the type on the right of the
assignment operator (=) must match, except in cases of automatic
casting, like storing an int value into a double variable. Since
they have the same type, it makes sense to store an element of an int
array like numbers[4] into an int variable like x. However, an
array of int values can’t be stored into an int type.
int z = numbers;This code will cause a compiler error. What would it mean? You can’t put a list of variables into a single variable. And the converse is true as well.
numbers = 31;This code will also cause a compiler error. A single value can’t be stored into a whole list. You would have to specify an index where it can be stored. Furthermore, you must be careful to specify a legal index. No negative index will ever be legal, and neither will an index greater than or equal to the number of elements in the array.
numbers[10] = 99;This code will compile correctly. If you remember, we instantiated the
array that numbers points at to have 10 elements, numbered 0 through
9. Thus, we are trying to store 99 into the element that is one index
after the last legal element. As a result, Java will cause an error
called an ArrayIndexOutOfBoundsException to happen, which will crash
your program.
6.4.3. Using loops with arrays
One reason to use arrays is to avoid declaring 10 separate variables
just to have 10 int values to work with. But once you have the array,
you’ll often need an automated way to process it. Any of the three
kinds of loops provides a powerful tool for performing operations on an
array, but the for loop is an especially good match. Here is an
example of a for loop that sets the values in an array to their
indexes.
int[] values = new int[100];
for(int i = 0; i < 100; i++)
values[i] = i;This sample of code shows how easy it is to iterate over every element
in an array with a for loop, but it has a flaw in its style. Note that
the number 100 is used twice: once in the instantiation of the array
and a second time in the termination condition of the for loop. This
fragment of code works fine, but if the programmer changes the length of
values to be 50 or 500, the bounds of the for loop will also
need to change. Furthermore, the length of the array might be determined
by user input.
To make the code both more robust and readable, we can use the length
field of the values array for the bound of the for loop.
int[] values = new int[100];
for(int i = 0; i < values.length; i++)
values[i] = i;The length field gives the length of the array that values points
to. If the programmer wants to instantiate the array with a different
length, that’s fine. The length field will always reflect the correct
value. Whenever possible, use the length field of arrays in your code.
Note that the length field is read-only. If you try to set
values.length to a specific value, your code will not compile.
Setting the values in an array is only one possible task you can perform
with a loop. Let’s assume that an array of type double named data
has been declared, instantiated, and filled with user input. We could
sum all its elements using the following code. A more elegant way to do
the same summation is discussed in Section 6.9.1.
double sum = 0.0;
for(int i = 0; i < data.length; i++)
sum += data[i];
System.out.println("The sum of your data is: " + sum);So far, we’ve only discussed operations on the values in an array. It
is important to realize that the order of those values can be equally
important. We’re going to create an array of char type named
letters, initialized with some values, and then reverse the order of
the array.
char[] letters = {'b', 'y', 'z', 'a', 'n', 't', 'i', 'n', 'e'}; (1)
int start = 0; (2)
int end = letters.length - 1; (3)
char temp;
while(start < end) { (4)
temp = letters[start]; (5)
letters[start] = letters[end];
letters[end] = temp;
start++; (6)
end--;
}
for(int i = 0; i < letters.length; i++) (7)
System.out.print(letters[i]);| 1 | After initializing the letters
array, we declare start and end. |
| 2 | start gets the value 0, the
first index of letters. |
| 3 | end gets the value letters.length - 1, the last valid index
of letters. |
| 4 | The while loop continues as long as
the start is less than the end. |
| 5 | The first three lines of each
iteration of the while loop will swap the char at index start with
the char at index end. |
| 6 | The two lines after that will increment and
decrement start and end, respectively. When the two meet in the
middle, the entire array has been reversed. |
| 7 | The simple for loop at the
end prints out each char in letters, giving the output enitnazyb. |
Of course, we could have printed out the array elements in reverse order without changing their order, but we wanted to reverse them, perhaps because we will need them reversed in the future.
6.4.4. Redirecting input
With arrays and loops, we can process a lot of data, but testing programs that process a lot of data can be tedious. Instead of typing data into the terminal, we can read data from a file. In Java, file I/O is a messy process that involves several objects and method calls. We’re going to talk about it in depth in Chapter 20, but for now we can use a quick and easy workaround.
If you create a text file using a simple text editor, you can redirect
the file as input to a program. Everything you’ve written in the text
file is treated as if it were being typed into the command line by a
person. To do so, you type the command using java to run your class
file normally, type the < sign, and then type the name of the file you
want to use as input. For example, if you have a text file called
numbers.txt that you want to use as input to a program stored in
Summer.class, you could do so as follows.
java Summer < numbers.txt
Redirecting input this way is not a part of Java. Instead, it’s a feature of the terminal running under your OS. Not all operating systems support input redirection, but virtually every flavor of Linux and Unix do, as well as the Windows command line and the macOS terminal. We could write the program mentioned above and give it the simple task of summing all the numbers it gets as input.
import java.util.*;
public class Summer {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("How many numbers do you want to add? ");
int n = in.nextInt();
int sum = 0;
for(int i = 0; i < n; i++) {
System.out.print("Enter next number: ");
sum += in.nextInt();
}
System.out.println("The sum of the numbers is " + sum);
}
}Now, we can type out a file with a list of numbers in it and save it as
numbers.txt. To conform with the program we wrote, we should also put
the total count of numbers as the first value in the file. You can put
each number on a separate line or just leave a space between each one.
As long as they are separated by white space, the Scanner object will
take care of the rest. You’ll have to type the numbers into the file
once, but then you can test your program over and over with the same file.
If you do run the program with the file you’ve created, you’ll notice
that the program still prompts you once for the total count of numbers
and then prompts you many times to enter the next number. With
redirected input, all that text runs together in a bizarre way. All the
input is coming from numbers.txt. If you expect a program to read
strictly from redirected input, you can design your code a little
differently. For one thing, you don’t need to have explicit prompts for
the user. For another, you can use a number of special methods from the
Scanner class. The Scanner class has a several methods like
hasNextInt() and hasNextDouble(). These methods will examine the
input and see if there is another legal int or double and return
true or false accordingly. If you expect a file to have only a long
sequence of int values, you can use hasNextInt() to determine if
you’ve reached the end of the file or not. Using hasNextInt(), we can
simplify the program and remove the expectation that the first number
gives the total count of numbers.
import java.util.*;
public class QuietSummer {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int sum = 0;
while(in.hasNextInt())
sum += in.nextInt();
System.out.println("The sum of the numbers is " + sum);
}
}On the other hand, you might be interested in the output of a program.
The output could be very long or it might take a lot of time to produce
or you might want to store it permanently. For these situations, it is
possible to redirect output as well. Instead of printing to the
screen, you can send the output to a file of your choosing. The syntax
for this operation is just like the syntax for input redirection except
that you use the > sign instead of <. To run QuietSummer with
input from numbers.txt and output to sum.txt, we could do the
following.
java QuietSummer < numbers.txt > sum.txt
You would be free to examine sum.txt at any time with your text editor
of choice. When using output redirection, it makes more sense to run
QuietSummer than Summer. If we had run Summer, all of that
unnecessary output prompting the user to enter numbers would be saved in
sum.txt.
6.5. Examples: Array usage
Here are a few examples of practical array usage. We’re going to discuss some techniques useful mostly for searching and sorting. Searching for values in a list seems mundane, but it’s one of the most practical tasks that a computer scientist routinely carries out. By making a computer do the work, it saves human beings countless hours of tedious searching and checking. Another important task is sorting. Sorting a list can make future searches faster and is the simplest way to find the median of a list of values. Sorting is a fundamental part of countless real world problems.
In the examples below, we’ll first discuss finding the largest (or smallest) value in a list, move on to sorting lists, and then talk about a task that searches for words, like a dictionary look up.
Finding the largest value input by a user is not difficult. Applying
that knowledge to an array is pretty straightforward as well. This
simple task is also a building block of the sorting algorithm we’ll
discuss below. The key to finding the largest value in any list is to
keep a temporary variable that records the largest value found so far.
As we go along, we update the variable if we find a larger value. The
only trick is initializing the variable to some appropriate starting
value. We could initialize it to zero, but what if entire list of
numbers is negative? Then, our answer would be larger than any of the
numbers in the list. If our list of numbers is of type int, we could
initialize our variable to Integer.MIN_VALUE, the smallest possible
int. This approach works, but you have to remember the name of the
constant, and it doesn’t improve the readability of the code.
When working with an array, the best way to find the largest value in
the list is by setting your temporary variable to the first element
(index 0) in the array. Below is a short snippet of code that finds
the largest value in an int array named values in exactly this way.
int largest = values[0];
for(int i = 1; i < values.length; i++)
if(values[i] > largest)
largest = values[i];
System.out.println("The largest value is " + largest);Note that the for loop starts at 1 not 0. Because largest is
initialized to be values[0], there’s no reason to check that value a second time.
Doing so would still give the correct answer, but it wastes a tiny
amount of time.
What’s the feature of this code that makes it find the largest value?
The key is the > operator. With the change of a single character, we
could find the smallest value instead.
int smallest = values[0];
for(int i = 1; i < values.length; i++)
if(values[i] < smallest)
smallest = values[i];
System.out.println("The smallest value is " + smallest);In addition to the necessary change from > to <, we also changed the
output and the name of the variable to avoid confusion. Now, we’ll show
how repeatedly finding the smallest value in an array can be used to
sort it. Alternatively, the largest value could be used equally well.
Sorting is the bread and butter of computer scientists. Much research has been devoted to finding the fastest ways to sort a list of data. The rest of the world assumes that sorting a list of data is trivial because computer scientists have done such a good job solving this problem. The name of the sorting algorithm we are going to describe below is selection sort. It’s not one of the fastest ways to sort data, but it’s simple and easy to understand.
The idea behind selection sort is to find the smallest element in an
array and put it at index 0 of the array. Then, from the remaining
elements, find the smallest element and put it at index 1 of the
array. The process continues, filling the array up from the beginning
with the smallest values until the entire array is sorted. If the length
of the array is n, we’ll need to look for the smallest
element in the array n - 1 times. By putting the code that
searches for the smallest value inside of an outer loop, we can write a
program that does selection sort of int values input by the user as
follows. This program’s not very long, but there’s a lot going on.
import java.util.*;
public class SelectionSort {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(); (1)
int[] values = new int[n]; (2)
int smallest;
int temp;
for(int i = 0; i < values.length; i++) (3)
values[i] = in.nextInt();| 1 | After
instantiating a Scanner, we read in the total number of values the
list will hold. We cannot rely on the hasNextInt() method to tell us
when to stop reading values. |
| 2 | We need to know up front how many values we are going to store so that we can instantiate our array with the appropriate length. |
| 3 | Then, we read each value into the array using the
first for loop. |
for(int i = 0; i < n - 1; i++) { (1)
smallest = i;
for(int j = i + 1; j < n; j++) (2)
if(values[j] < values[smallest])
smallest = j; (3)
temp = values[smallest]; (4)
values[smallest] = values[i];
values[i] = temp;
}| 1 | The next for loop is where the actual sort happens. We start at index
0 and then try to find the smallest value to be put in that spot.
Then, we move on to index 1, and so on, just as we described before.
Note that we only go up to n - 2. We don’t need to find the value to
put in index n - 1, because the rest of the list has the n - 1
smallest numbers in it and so the last number must already be the
largest. |
| 2 | If you look carefully, you’ll notice that the inner for
loop has the same overall shape as the loop used to find the smallest
value in the previous example; however, there is one key difference: |
| 3 | Instead of storing the value of the smallest number in smallest, we
now store the index of the smallest number. We need to store the index
of the smallest number so that, in the next step, we can swap the
corresponding element with the element at i, the spot in the array
we’re trying to fill. |
| 4 | The three lines after the inner for loop are a
simple swap to do exactly that. |
System.out.print("The sorted list is: ");
for(int i = 0; i < values.length; i++) (1)
System.out.print(values[i] + " ");
}
}| 1 | After all the sorting is done, the final for loop prints out the newly
sorted list. |
This program gives no prompts for user input, so it’s well designed for input redirection. If you’re going to make a file containing numbers you want to sort with this program, make sure that the first number is the total count of numbers in the file.
Again, this program sorts the list in ascending order (from smallest to
largest). If you wanted to sort the list in descending order, you would
only need to change the < to a > in the comparison of the inner
for loop, although other changes are recommended for the sake of
readability.
In this example, we read in a list of words and a long passage of text and keep track of the number of times each word in the list occurs in the passage. This kind of text searching has many applications. Similar ideas are used in a spell checker that needs to look up words in a dictionary. The incredibly valuable find and replace tools in modern word processors use some of the same techniques.
To make this program work, however, we need to read in a (potentially long) list of words and then a lot of text. We are forced to use input redirection (or some other file input) because typing this text in multiple times would be tedious. When we get to Chapter 20, we’ll talk about ways to read from multiple files at the same time. Right now, we can only redirect input from a single file, and so we’re forced to put the list of words at the top of the file, followed by the text we want to search through.
import java.util.*;
public class WordCount {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(); (1)
String[] words = new String[n]; (2)
int[] counts = new int[n]; (3)
String temp;
for(int i = 0; i < words.length; i++) (4)
words[i] = in.next().toLowerCase();| 1 | As in the last example, this program begins by reading in the length of the list of words. |
| 2 | Then, it instantiates the String array words to
hold these words. |
| 3 | It also instantiates an array counts of type int
to keep track of the number of times each word is found. By default,
each element in counts is initialized to 0. |
| 4 | The first for loop in
the program reads in each word and stores it into the array words. |
while(in.hasNext()) { (1)
temp = in.next().toLowerCase();
for(int i = 0; i < n; i++) (2)
if(temp.equals(words[i])) {
counts[i]++; (3)
break;
}
}
System.out.println("The word counts are: ");| 1 | The while loop reads in each word from the text following the list and
stores it in a variable called temp. |
| 2 | Then, it loops through words
and tests to see if temp matches any of the elements in the list. |
| 3 | If it does, it increases the value of the element of counts that has the
same index and breaks out of the inner for loop. |
for(int i = 0; i < words.length; i++) (1)
System.out.println(words[i] + " " + counts[i]);
}
}| 1 | After all the words in the text have been processed, the final for
loop prints out each word from the list, along with its counts. |
This program uses two different arrays for bookkeeping: words contains
the words we are searching for and counts contains the number of times
each word has been found. These two arrays are separate data structures.
The only link between them is the code we wrote to maintain the
correspondence between their elements.
To give a clear picture of how this program should behave, here’s a sample input file with two paragraphs from the beginning of The Count of Monte Cristo by Alexandre Dumas.
7 and at bridge for pilot vessel walnut On the 24th of February, 1815, the look-out at Notre-Dame de la Garde signaled the three-master, the Pharaon from Smyrna, Trieste, and Naples. As usual, a pilot put off immediately, and rounding the Chateau d'If, got on board the vessel between Cape Morgion and Rion island. Immediately, and according to custom, the ramparts of Fort Saint-Jean were covered with spectators; it is always an event at Marseilles for a ship to come into port, especially when this ship, like the Pharaon, has been built, rigged, and laden at the old Phocee docks, and belongs to an owner of the city.
And here’s the output one should get from running WordCount with
input redirected from the file given above.
The word counts are: and 6 at 3 bridge 0 for 1 pilot 1 vessel 1 walnut 0
For this example, the program works fine. However, our program would
have given incorrect output if ship, spectators, or several other
words in the text had been on the word list. You see, the next()
method in the Scanner class reads in String values separated by
white space. The word ship appears twice in the text, but the second
instance is followed by a comma. Since the words are separated by white
space only, the String "ship," does not match the String "ship".
Dealing with punctuation is not difficult, but it would increase the
length of the code, so we leave it as an exercise.
Imagine you’re a teacher who has just given an exam. You want to produce statistics for the class so that the students have some idea how well they have done. You want to write a Java program to help you produce the statistics, to save time now and in the future.
The statistics you want to collect are listed in the following table.
| Statistic | Description |
|---|---|
Maximum |
Maximum score |
Minimum |
Minimum score |
Mean |
Average of all the scores |
Standard Deviation |
Sample standard deviation of the scores |
Median |
Middle value of the scores when ordered |
Example 6.1 covered how to find the maximum and minimum scores in a list. The mean is simply the sum of all the scores divided by the total number of scores. Standard deviation is a little bit trickier. It gives a measurement of how spread out the data is. Let n be the number of data points, label each data point xi, where 1 ≤ i ≤ n, and let μ be the mean of all the data points. Then, the formula for the sample standard deviation is as follows.

Finally, if you sort a list of numbers in order, the median is the middle value in the list, or the average of the two middle values, if the list has an even length.
These kinds of statistical operations are useful and are packaged into many important business applications such as Microsoft Excel. This version will have a simple interface whose input comes from the command line. First, the total number of scores will be entered. Then, each score should be entered one by one. After all the data has been entered, the program should compute and output the five values.
Below we give the solution to this statistics problem. Several different tasks are combined here, but each of them should be reasonably easy to solve after the previous examples.
import java.util.*;
public class Statistics {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(); (1)
int[] scores = new int[n]; (2)
for(int i = 0; i < n; i++) (3)
scores[i] = in.nextInt();| 1 | In our solution, the main() method begins by reading in the total
number of scores. |
| 2 | It declares an int array of that length named
scores. |
| 3 | Then, we read in each of the scores and store them into
scores. |
int max = scores[0]; (1)
int min = scores[0];
int sum = scores[0];
for(int i = 1; i < n; i++) { (2)
if(scores[i] > max)
max = scores[i];
if(scores[i] < min)
min = scores[i];
sum += scores[i];
}| 1 | Here we declare variables max, min, and sum to hold, respectively,
the maximum, minimum, and sum of the elements in the array. Then, we set
all three variables to the value of the first element of the array.
These initializations make the following code work. |
| 2 | In a single for
loop, we find the maximum, minimum, and sum of all the values in the
array. |
We could have done so with three separate loops, but this
approach is more efficient. Setting max and min to scores[0]
follows the pattern we’ve used before, but setting sum to the same
value is also necessary in this case. Because the loop iterates from 1
up to scores.length - 1, we must include the value at index 0 in
sum. Alternatively, we could have set sum to 0 and started the
for loop at i = 0.
double mean = ((double)sum)/n;
System.out.println("Maximum:\t\t" + max);
System.out.println("Minimum:\t\t" + min);
System.out.println("Mean:\t\t\t" + mean);In this short snippet of code, we compute the mean, being careful to
cast it into type double before the division, and then print out the three
statistics we’ve computed.
double variance = 0;
for(int i = 0; i < n; i++)
variance += (scores[i] - mean)*(scores[i] - mean); (1)
variance /= (n - 1); (2)
System.out.println("Standard Deviation:\t" + Math.sqrt(variance)); (3)| 1 | At this point, we use the mean we’ve already computed to find the
sample standard deviation. Following the formula for sample standard
deviation, we subtract the mean from each score, square the result, and
add it to a running total. Although the formula for sample standard
deviation uses the bounds 1 to n, we
translate them to 0 to n - 1 because of zero-based array numbering. |
| 2 | Dividing the total by n - 1 gives the sample variance. |
| 3 | Then, the square root of the variance is the standard deviation. |
int temp;
for(int i = 0; i < n - 1; i++) { (1)
min = i;
for(int j = i + 1; j < n; j++)
if(scores[j] < scores[min])
min = j;
temp = scores[min];
scores[min] = scores[i];
scores[i] = temp;
}| 1 | To find the median, we use our selection sort code. |
Note that we have
reused the variable min to hold the smallest value found so far,
instead of declaring a new variable such as smallest. Some programmers
might object to doing so, since we run the risk of interpreting the
variable as the minimum value in the entire array, as it was before.
Either approach is fine. If you worry about confusing people reading
your code, add a comment.
double median;
if(n % 2 == 0) (1)
median = (scores[n/2] + scores[n/2 + 1])/2.0; (2)
else
median = scores[n/2]; (3)
System.out.println("Median:\t\t\t" + median);
}
}| 1 | After the array has been sorted, we need to do a quick check to see if its length is odd or even. |
| 2 | If its length is even, we need to find the average of the two middle elements. |
| 3 | If its length is odd, we can report the value of the single middle element. |
Note that some of the statistics we found, such as the maximum, minimum, or mean, could be computed with a single pass over the data without the need for an array for storage. However, the last two tasks need to store all the values to work. The simplest way to find the sample standard deviation of a list of values requires its mean, requiring one pass to find the mean and a second to sum the squares of the difference of the mean and each value. Likewise, it’s impossible to find the median of a list of values without storing the list.
6.6. Concepts: Multidimensional lists
In the previous half of the chapter, we focused on lists of data and how to store them in Java in arrays. The arrays we have discussed already are one-dimensional arrays. That is, each element in the array has a single index that refers to it. Given a specific index, an element will have that index, come before it, or come after it. These kinds of arrays can be used to solve a huge number of problems involving lists or collections of data.
Sometimes, the data needs to be represented with more structure. One way to provide this structure is with a two-dimensional array. You can think of a two-dimensional array as a table of data. Instead of using a single index, a two-dimensional array has two indexes. Usually, we think about these dimensions as rows and columns. Below is a table of information that gives the distances in miles between the five largest cities in the United States.
| New York | Los Angeles | Chicago | Houston | Phoenix | |
|---|---|---|---|---|---|
New York |
0 |
2,791 |
791 |
1,632 |
2,457 |
Los Angeles |
2,791 |
0 |
2,015 |
1,546 |
373 |
Chicago |
791 |
2,015 |
0 |
1,801 |
1,181 |
Houston |
1,632 |
1,546 |
1,801 |
0 |
1,176 |
Phoenix |
2,457 |
373 |
1,181 |
1,176 |
0 |
The position of each number in the table is a fundamental part of its
usefulness. We know that the distance from Chicago to Houston is 1,801
miles because that number is in the Chicago row and the Houston column.
A two-dimensional array shares almost all of its properties with a
one-dimensional array. It’s still a homogeneous, static data structure
with random access. If the example above were made into a Java array,
the numbers themselves would be the elements of the array. The names of
the cities would need to be stored separately, perhaps in an array of
type String.
There’s no reason to confine the idea of a two-dimensional list to a
table of values. Many games are played on a two-dimensional grid. One of
the most famous such games is chess. As with so many other things in
computer science, we must come up with an abstraction that mirrors
reality and allows us to store the information inside of a computer. For
chess, we’ll need an 8 × 8 two-dimensional array. We can represent
each piece in the board with a char, using the encoding given below.
| Piece | Encoding |
|---|---|
Pawn |
'P' |
Knight |
'N' |
Bishop |
'B' |
Rook |
'R' |
Queen |
'Q' |
King |
'K' |
Using uppercase characters for black pieces and lowercase characters for white pieces, we could represent a game of chess after a classic king’s pawn open by white as shown.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
0 |
'R' |
'N' |
'B' |
'Q' |
'K' |
'B' |
'N' |
'R' |
1 |
'P' |
'P' |
'P' |
'P' |
'P' |
'P' |
'P' |
'P' |
2 |
||||||||
3 |
||||||||
4 |
||||||||
5 |
'p' |
|||||||
6 |
'p' |
'p' |
'p' |
'p' |
'p' |
'p' |
'p' |
|
7 |
'r' |
'n' |
'b' |
'q' |
'k' |
'b' |
'n' |
'r' |
Observe that, just as with one-dimensional arrays, the indexes for rows and columns in two-dimensional arrays also use zero-based counting.
After the step from one-dimensional arrays to two-dimensional arrays, it’s natural to wonder if there can be arrays of even higher dimension. We can visualize a two-dimensional array as a table, but a three-dimensional array is harder to visualize. Nevertheless, there are uses for three-dimensional arrays.
Consider a professor who’s taking a survey of students in her course. She wants to know how many students there are in each of three categories: gender, class level, and major. If she treats each of these as a dimension and assigns an index to each possible value, she could store the results in a three-dimensional array. For gender she could pick male = 0 and female = 1. For class level she could pick freshman = 0, sophomore = 1, junior = 2, senior = 3, and other = 4. Assuming it’s a computer science class, for major she could pick computer science = 0, math = 1, other science = 2, engineering = 3, and humanities = 4. Using this system she could compactly store the number of students in any combination of categories she was interested in. For example, the total number of female sophomore engineering students would be stored in the cell with gender index 1, class level index 1, and major index 3.
Three dimensions is usually the practical limit when programming in Java. If you find an especially good reason to use four or higher dimensions, feel free to do so, but it should happen infrequently. The Java language has no set limit on array dimensions, but most virtual machines have the absurdly high limitation of 255 different dimensions.
6.7. Syntax: Advanced arrays in Java
Now that we’ve discussed the value of storing data in multidimensional lists, we’ll describe the Java language features that allow you to do so. The changes needed to go from one-dimensional arrays to two-dimensional and higher arrays are simple. First, we’ll describe how to declare, instantiate, and index into two-dimensional arrays. Then, we’ll discuss some of the ways in which arrays (both one-dimensional and higher) are different from primitive data types. Next, we’ll explain how it’s possible to make two-dimensional arrays in Java where the rows are not all the same length. Finally, we’ll cover some of the most common mistakes programmers make with arrays.
6.7.1. Multidimensional arrays
When declaring a two-dimensional array, the main difference from a
one-dimensional array is an extra pair of brackets. If we wish to
declare a two-dimensional array of type int in which we could store
values like the table of distances above, we would do so as follows.
int[][] distances;As with one-dimensional arrays, it’s legal to put the brackets on the other side of the variable identifier or, even more bizarrely, have a pair on each side.
Once the array is declared, it must still be instantiated using the
new keyword before it can be used. This time we will use two pairs of
brackets, with the number in the first pair specifying the number of
rows and the number in the second pair specifying the number of columns.
distances = new int[5][5];After the instantiation, we will have 5 rows and 5 columns, giving a
total of 25 locations where int values can be stored. Indexing these
locations is done by specifying row and column values in the brackets.
So, to fill up the table with the distances between cities given above
we can use the following tedious code.
// New York
distances[0][1] = 2791;
distances[0][2] = 791;
distances[0][3] = 1632;
distances[0][4] = 2457;
// Los Angeles
distances[1][0] = 2791;
distances[1][2] = 2015;
distances[1][3] = 1546;
distances[1][4] = 373;
// Chicago
distances[2][0] = 791;
distances[2][1] = 2015;
distances[2][3] = 1801;
distances[1][4] = 1181;
// Houston
distances[3][0] = 1632;
distances[3][1] = 1546;
distances[3][2] = 1801;
distances[3][4] = 1176;
// Phoenix
distances[4][0] = 2457;
distances[4][1] = 373;
distances[4][2] = 1181;
distances[4][3] = 1176;You’ll notice that we did not specify values for distances[0][0],
distances[1][1], distances[2][2], distances[3][3], or
distances[4][4], since each of these already has the default value of
0.
Much more often, multidimensional array manipulation will use nested
for loops. For example, we could create an array with 3 rows and 4
columns, and then assign values to those locations such that they were
numbered increasing across each row.
int[][] values = new int[3][4];
int number = 1;
for(int i = 0; i < values.length; i++)
for(int j = 0; j < values[i].length; j++) {
values[i][j] = number;
number++;
}This code would result in an array filled up like the following table.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
The bounds for the outer for loop in this example uses
values.length, giving the total number of rows. Then, the inner for
loops uses values[i].length, which is the length (number of columns)
of the current row. In this case, all the rows of the array have the same
number of columns, but this is not always true, as we’ll discuss
later.
6.7.2. Reference types
All array variables are reference type variables, not simple values
like most of the types we have discussed so far. A reference variable is
a name for an object. You might recall that we described the difference
between reference types and primitive types in
Section 3.2, but the only reference type we’ve
considered in detail is String.
More than one reference variable can point at the same object. When one
object has more than one name, this is called aliasing. The String
type is immutable, meaning that an object of type String cannot change
its contents. Arrays, however, are mutable, which means that aliasing
can cause unexpected results. Here is a simple example with
one-dimensional array aliasing.
int[] array1 = new int[10];
for(int i = 0; i < array1.length; i++)
array1[i] = i;
int[] array2 = array1;
array2[3] = 17;
System.out.println(array1[3]);Surprisingly, the value printed out will be 17. The variables array1
and array2 are references to the same fundamental array. Unlike
primitive values, the complete contents of array1 are not copied to
array2. Only one array exists because only one array has been created
by the new keyword. When index 3 of array2 is updated, index 3
of array1 changes as well, because the two variables are simply two
names for the same array.

Sometimes this reference feature of Java allows us to write code that is confusing or has unexpected consequences. However, the benefit is that we can assign one array to another without incurring the expense of copying the entire array. If you create an array with 1,000,000 elements, copying that array several times could get expensive in terms of program running time.
The best rule of thumb for understanding reference types is that there
is only one actual object for every call to new. The primary exception
to this rule is that uses of new can be hidden from the user when
they’re in method calls.
String greeting = new String("Hello");
String pronoun = greeting.substring(0,2);At the end of this code, the reference pronoun will point to an object
containing the String "He". The substring() method invokes new
internally, generating a new String object completely separate from
the String referenced by greeting. This code may look unusual
because we’re explicitly using new to make a String object
containing "Hello". The String class is different from every other
class because it can be instantiated without using the new keyword.
The line String greeting = "Hello"; implicitly calls new to create an object
containing the String "Hello" and functions nearly the same as the
similar line above.
6.7.3. Ragged arrays
We’re ashamed to say that we’ve lied to you. In Java, there’s no such thing as a true multidimensional array! Instead, the examples of two-dimensional and three-dimensional arrays we’ve given above are actually arrays of arrays (of arrays). Thinking about multidimensional arrays in this way can give the programmer more flexibility.
If we return to the definition of the two-dimensional array with 3 rows and 4 columns, we can instantiate each row separately instead of as a block.
int[][] values = new int[3][];
int number = 1;
for(int i = 0; i < values.length; i++) {
values[i] = new int[4];
for(int j = 0; j < values[i].length; j++) {
values[i][j] = number;
number++;
}
}This code is functionally equivalent to the earlier code that instantiated all 12 locations at once. The same could be done with a three-dimensional array or higher. We can specify the length of each row independently, and, more bizarrely, we can give each row a different length. A multidimensional array whose rows have different lengths is called a ragged array.
A ragged array is usually unnecessary. The main reason to use a ragged array is to save space, when you have tabular data in which the lengths of each row vary a great deal. If the lengths of the rows vary only a little, it’s probably not worth the extra hassle. However, if some rows have 10 elements and others have 1,000,000, the space saved can be significant.
We can apply the idea of ragged arrays to the table of distances between cities. If you examine this table, you’ll notice that about half the data in it is repeated, because the distance from Chicago to Los Angeles is the same as the distance from Los Angeles to Chicago, and so on. We can store the data in a triangular shape to keep only the unique distance information.
| New York | Los Angeles | Chicago | Houston | Phoenix | |
|---|---|---|---|---|---|
New York |
0 |
||||
Los Angeles |
2,791 |
0 |
|||
Chicago |
791 |
2,015 |
0 |
||
Houston |
1,632 |
1,546 |
1,801 |
0 |
|
Phoenix |
2,457 |
373 |
1,181 |
1,176 |
0 |
We could create this table in code by doing the following.
distances = new int[5][];
// New York
distances[0] = new int[1];
// Los Angeles
distances[1] = new int[2];
distances[1][0] = 2791;
// Chicago
distances[2] = new int[3];
distances[2][0] = 791;
distances[2][1] = 2015;
// Houston
distances[3] = new int[4];
distances[3][0] = 1632;
distances[3][1] = 1546;
distances[3][2] = 1801;
// Phoenix
distances[4] = new int[5];
distances[4][0] = 2457;
distances[4][1] = 373;
distances[4][2] = 1181;
distances[4][3] = 1176;With this table a user cannot simply type in distances[0][4] and hope
to get the distance from New York to Phoenix. Instead, we have to be
careful to make sure that the index of the first city is never larger
than the index of the second city. If we’re reading in the indexes of
the cities from a user, we can write some code to do this check. Let
city1 and city2, respectively, contain the indexes of the cities the
user wants to use to find the distances between.
if(city1 > city2) {
int temp = city1;
city1 = city2;
city2 = temp;
}
System.out.println("The distance is: " + distances[city1][city2] +
" miles");If we wanted to be even cleverer, we could eliminate the zero entries from the table, but then the ragged array would have one fewer row than the original two-dimensional array.
6.7.4. Common pitfalls
Even one-dimensional arrays make many new errors possible. Below we list two of the most common mistakes made with both one-dimensional and multidimensional arrays.
|
Pitfall: Array out of bounds
The length of an array is determined at run time. Sometimes the number is
specified in the source code, but it’s always possible for an array to
be instantiated based on user input. The Java compiler doesn’t do any
checking to see if you’re in the right range. If your program tries to
access an illegal element, it’ll crash with an
Here’s a classic example. By iterating through the loop one too many
times, the program will try to store There are other less common causes for going outside of array bounds. Imagine that you’re scanning through a file that has been redirected to input, keeping a count of the occurrences of each letter of the alphabet in the file. This segment of code does a decent job of counting the occurrences of
each letter. The |
|
Pitfall: Uninitialized reference arrays
Another problem only comes up with arrays of reference types. Whenever
the elements of an array are primitive data types, memory for that type
is allocated. Whenever the elements of the array are reference types,
only references to objects, initialized to The following code, however, will cause a Arrays of reference types must initialize each element before using it.
The In this case, there would be no error, although
A similar error can happen with multidimensional arrays. Because an array is itself a reference type, the |
6.8. Examples: Two-dimensional arrays
Below we give some examples where two-dimensional arrays can be helpful. We start with a simple calendar example, move on to matrix and vector multiplication useful in math, and finish with a game.
We’re going to create a calendar that can be printed to the terminal to show which day of the week each day lands on. Our program will prompt the user for the day of the week the month starts on and for the total number of days in the month. Our program will print out labels for the seven days of the week, followed by numbering starting at the appropriate place, and wrapping such that each numbered day of the month falls under the appropriate day of the week.
import java.util.*;
public class Calendar {
public static void main(String[] args) {
String[][] squares = new String[7][7]; (1)
squares[0][0] = "Sun"; (2)
squares[0][1] = "Mon";
squares[0][2] = "Tue";
squares[0][3] = "Wed";
squares[0][4] = "Thu";
squares[0][5] = "Fri";
squares[0][6] = "Sat";
for(int i = 1; i < squares.length; i++) (3)
for(int j = 0; j < squares[i].length; j++)
squares[i][j] = " ";
Scanner in = new Scanner(System.in);
System.out.print("Which day does your month start on? (0 - 6) ");
int start = in.nextInt(); //read starting day (4)
System.out.print("How many days does your month have? (28 - 31) ");
int days = in.nextInt(); //read days in month (5)
int day = 1;
int row = 1;
int column = start;
while(day <= days) { //fill calendar (6)
squares[row][column] = "" + day;
day++;
column++;
if(column >= squares[row].length) {
column = 0;
row++;
}
}
for(int i = 0; i < squares.length; i++) { (7)
for(int j = 0; j < squares[i].length; j++)
System.out.print(squares[i][j] + "\t");
System.out.println();
}
}
}| 1 | First, our code creates a 7 × 7 array of type
String called squares. The array needs 7 rows so that it can start
with a row to label the days and then output up to 6 rows to cover the
weeks. (Months with 31 days span parts of 6 different weeks if they
start on a Friday or a Saturday.) The number of columns corresponds to
the seven days of the week. |
| 2 | Next, we initialize the first row of the array to abbreviations for each day of the week. |
| 3 | Then, we initialize the rest of the array to be a single space. |
| 4 | Our program then reads from the user the day the month starts on. |
| 5 | The program also reads from the user for the total number of days in the month. |
| 6 | The main work of the program is done by the while loop, which fills
each square with a steadily increasing day number for each column,
moving on to the next row when a row is filled. |
| 7 | Finally, the two nested for loops at the end print out the contents of squares, putting a
tab ('\t') between each column and starting a new line for each row. |
Arrays give a natural way to represent vectors and matrices. In 3D graphics and video game design, we can represent a point in 3D space as a vector with three elements: x, y, and z. If we want to rotate the three-dimensional point represented by this vector, we can multiply it by a matrix. For example, to rotate a point around the x-axis by θ degrees, we could use the following matrix.

Given an m × n matrix A, let Aij be the element in the ith row, jth column. Given a vector v of length n, let vi be the ith element in the vector. To multiply A by v, we use the following equation to find the ith element of the resulting vector v′.

By transforming this equation to Java code, we can write a program that can read in a three-dimensional point and rotate it around the x-axis by the amount specified by the user.
import java.util.*;
public class MatrixRotate {
public static void main(String[] args) {
double[] point = new double[3]; (1)
System.out.println("What point do you want to rotate?");
Scanner in = new Scanner(System.in);
System.out.print("x: "); (2)
point[0] = in.nextDouble();
System.out.print("y: ");
point[1] = in.nextDouble();
System.out.print("z: ");
point[2] = in.nextDouble();
System.out.print("What angle around the x-axis? ");
double theta = Math.toRadians(in.nextDouble()); (3)
double[][] rotation = new double[3][3];
rotation[0][0] = 1; (4)
rotation[1][1] = Math.cos(theta);
rotation[1][2] = -Math.sin(theta);
rotation[2][1] = Math.sin(theta);
rotation[2][2] = Math.cos(theta);
double[] rotatedPoint = new double[3];
for(int i = 0; i < rotatedPoint.length; i++) (5)
for(int j = 0; j < point.length; j++)
rotatedPoint[i] += rotation[i][j]*point[j];
System.out.println("Rotated point: [" + rotatedPoint[0] + (6)
"," + rotatedPoint[1] + "," + rotatedPoint[2] + "]");
}
}| 1 | This program begins by declaring a array of type double to hold the
vector. |
| 2 | Afterward, it reads three values from the user into it. |
| 3 | Then, the program reads in the angle of rotation in degrees and converts it to radians. |
| 4 | Next, we use the Math class to calculate the values in the
rotation matrix. Note that we do not change the values that need to be
zero. |
| 5 | We use a for loop to perform the matrix-vector
multiplication. Again, the summing done by
our calculations uses the fact that all elements of rotatedPoint are
initialized to 0.0. |
| 6 | Finally, we print out the answer. |
Almost every child knows the game of tic-tac-toe, also known as noughts and crosses. Its playing area is a 3 × 3 grid. Players take turns placing Xs and Os, trying to get three in a row. Strategically, it’s not the most interesting game since two players who make no mistakes will always tie. Still, we present a program that allows two human players to play the game because the manipulations of a two-dimensional array in the program are similar to those for more complicated games such as Connect Four, checkers, chess, or Go. Our program will catch any attempt to play on a location that has already been played and will determine the winner, if there is one.
Games often give rise to complex programs, since rules that are intuitively obvious to humans may be difficult to state explicitly in Java. Our program begins by setting up quite a few variables and objects.
import java.util.*;
public class TicTacToe {
public static void main(String[] args) {
Scanner in = new Scanner(System.in); (1)
char[][] board = new char[3][3]; (2)
for(int i = 0; i < board.length; i++) (3)
for(int j = 0; j < board[0].length; j++)
board[i][j] = ' ';
boolean turn = true; (4)
boolean gameOver = false;
int row, column, moves = 0; (5)
char shape;| 1 | First, we create a Scanner to read in data. |
| 2 | Then, we declare
and instantiate our 3 × 3 playing board as a
two-dimensional array of type char. |
| 3 | We want any unplayed space on the
grid to be the char for a space, so we fill the array with ' '. |
| 4 | Next, we declare a boolean value to keep track of whose turn it is and
another to keep track of whether the game is over. |
| 5 | Finally, we
declare variables to hold the row, the column, the number of moves that
have been made so far and the current shape ('X' or 'O'). |
The core of the game is a while loop that runs until gameOver
becomes true. The first line of the body of this loop is an obscure
Java shortcut often referred to as the ternary operator. This line is
really shorthand for the following.
if(turn)
shape = 'X';
else
shape = '0';The ternary operator works with a condition followed by a question mark
and then two values separated by a colon. If the condition is true,
the first value is assigned, otherwise the second value is assigned.
It’s perfect for situations like this where one value is needed when
turn is true and another is needed when turn is false. The
ternary operator is a useful trick, but it shouldn’t be overused.
while(!gameOver) {
shape = turn ? 'X' : 'O';
System.out.print(shape + "'s turn. Enter row (0-2): "); (1)
row = in.nextInt();
System.out.print("Enter column (0-2): ");
column = in.nextInt();
if(board[row][column] != ' ') (2)
System.out.println("Illegal move");
else {
board[row][column] = shape; (3)
moves++;
turn = !turn;
// Print board (4)
System.out.println(board[0][0] + "|"
+ board[0][1] + "|" + board[0][2]);
System.out.println("-----");
System.out.println(board[1][0] + "|"
+ board[1][1] + "|" + board[1][2]);
System.out.println("-----");
System.out.println(board[2][0] + "|"
+ board[2][1] + "|" + board[2][2] + "\n"); | 1 | After assigning the appropriate value to shape, our code reads in the
row and column values for the current player’s next move. |
| 2 | If the row and column selected correspond to a spot that’s already been taken, the program gives an error message. |
| 3 | Otherwise, the program sets
board[row][column] to the appropriate symbol, increments moves, and
changes the value of turn. |
| 4 | Then, it prints out the board. |
Our program doesn’t do any bounds checking on row and column.
If a user tries to place a move at row 5 column 3, our program will try
to do so and crash. Additional clauses in the if statement could
be used to add bounds checking.
Perhaps the trickiest part of our tic-tac-toe program is checking for a win.
// Check rows (1)
for(int i = 0; i < board.length; i++)
if(board[i][0] == shape && board[i][1] == shape
&& board[i][2] == shape)
gameOver = true;
// Check column (2)
for(int i = 0; i < board[0].length; i++)
if(board[0][i] == shape && board[1][i] == shape
&& board[2][i] == shape)
gameOver = true;
// Check diagonals (3)
if(board[0][0] == shape && board[1][1] == shape
&& board[2][2] == shape)
gameOver = true;
if(board[0][2] == shape && board[1][1] == shape
&& board[2][0] == shape)
gameOver = true;
if(gameOver) (4)
System.out.println(shape + " wins!");
else if(moves == 9){ (5)
gameOver = true;
System.out.println("Tie game!");
}
}
}
}
}| 1 | First we check each row to see if it contains three in a row. |
| 2 | Then, we check each column. |
| 3 | Finally, we check the two diagonals. |
| 4 | If any of those checks ended the game, we announce a winner. |
| 5 | Otherwise, if the number of moves has reached 9 with no winner, it must be a tie game. |
In a larger game (such as Connect Four), we would want to find better ways to automate checking rows, columns, and diagonals. For example, we wouldn’t want to check the entirety of a larger board each move. Instead, we could focus only on the rows, columns, and diagonals affected by the last move.
6.9. Advanced: Special array tools in Java
Arrays are fundamental data structures in many programming languages.
There are often special syntactical tools or libraries designed to make
them easier to use. In this section, we explore two advanced tools, the
enhanced for loop and the Arrays utility class.
6.9.1. Enhanced for loops
In Chapter 5 we described three loops: while
loops, for loops, and do-while loops. Although these are the only
three loops in Java, there’s a special form of the for loop designed
for use with arrays (and some other data structures). This construct is
often called the enhanced for loop.
An enhanced for loop does not have the three-part header of a regular for
loop. Instead, it’s designed to iterate over the contents of an array or other list.
Inside its parentheses is a declaration of a variable with the same type
as the elements of the array, then a colon (:), then the name of the
array. Consider the following example of an enhanced for loop used to sum the
values of an array of int values called array. As with all loops in
Java, braces are optional if there’s only one executable statement in
the loop.
int sum = 0;
for(int value : array)
sum += value;This code functions in exactly the same way as the traditional for
loop we would use to solve the same problem.
int sum = 0;
for(int i = 0; i < array.length; i++)
sum += array[i];The advantage of the enhanced for loop is that it’s shorter and clearer.
There’s also no worry about being off by one with your indexes. The
enhanced for loop iterates over every element in the array, no indexes
needed!
Enhanced for loops can be nested or used inside of other loops. Consider the
following nested enhanced for loops that print out all possible chess
pieces, in both black and white colors.
String[] colors = {"Black", "White"};
String[] pieces = {"King", "Queen", "Rook", "Bishop", "Knight", "Pawn"};
for(String color : colors)
for(String piece : pieces)
System.out.println(color + " " + piece);Enhanced for loops do have a few drawbacks. For one, they’re designed for iterating
through an entire array. It’s ugly to try to make them stop early, and
it’s impossible to make them go back to previous values. They’re also
only designed for read access, not write access. The variable in the
header of the enhanced for loop takes on each value in the array in turn,
but assigning values to that variable has no effect on the underlying
array. Consider the following for loop that assigns 5 to every value
in array.
for(int i = 0; i < array.length; i++)
array[i] = 5;This kind of assignment is impossible in an enhanced for loop. The
“equivalent” enhanced for loop does nothing. It assigns 5 to the local
variable value but never changes the contents of array.
for(int value : array)
value = 5;While enhanced for loops are great for arrays, they can also be used for
any data structure that implements the Iterable interface. We
discuss interfaces in Chapter 10 and dynamic data
structures in Chapter 18 and
Chapter 19.
6.9.2. The Arrays class
The designers of the Java API knew that arrays were important and added
a special Arrays class to manipulate them.
This class has a number of static methods that can be used to search for
values in arrays, make copies of arrays, copy selected ranges of arrays,
test arrays for equality, fill arrays with specific values, sort arrays,
convert an entire array into a String representation, and more. The
signatures of the methods below are given for double arrays, but most
methods are overloaded to work with all primitive types and reference
types.
| Method | Purpose |
|---|---|
binarySearch(double[] array, double value) |
Returns index of |
copyOf(double[] array, int length) |
Returns a copy of |
copyOfRange(double[] array, int from, int to) |
Returns a copy of
|
equals(double[] array1, double[] array2) |
Returns |
fill(double[] array, double value) |
Fills |
sort(double[] array) |
Sorts |
toString(double[] a) |
Returns a |
Consult the API for more information. Even though tasks like fill()
are simple, it’s worth using the method from Arrays instead of
writing your own. The methods in the Java API have often been tuned for
speed and use special instructions that are not accessible to regular Java
programmers.
6.10. Solution: Game of Life
Here we present our solution to the Conway’s Game of Life simulation. Our program is designed to run the simulation with 24 rows and 80 columns, although it would be easy to change those dimensions.
public class Life {
public static void main(String[] args) {
final int ROWS = 24; (1)
final int COLUMNS = 80;
final int GENERATIONS = 500;
boolean[][] board = new boolean[ROWS][COLUMNS]; (2)
boolean[][] temp = new boolean[ROWS][COLUMNS];
boolean[][] swap;
for(int row = 0; row < ROWS; row++) (3)
for(int column = 0; column < COLUMNS; column++)
board[row][column] = (Math.random() < 0.1);| 1 | The main() method of our program starts by defining ROWS, COLUMNS,
and GENERATIONS as named constants using the final keyword. |
| 2 | Next, we
create two arrays with ROWS rows and COLUMNS columns. The board
array will hold the current generation. The temp array will be used to
fill in the next generation. Then, temp will be copied into board,
and the process will repeat. The swap variable is just a reference we’ll
use to swap board and temp. |
| 3 | We randomly fill the board, making 10% of the cells living. Again, you may wish to play with this number to see how the patterns in the simulation are affected. |
for(int generation = 0; generation < GENERATIONS; generation++) { (1)
for(int row = 0; row < ROWS; row++) (2)
for(int column = 0; column < COLUMNS; column++) {
int total = 0;
for(int i = Math.max(row - 1, 0); (3)
i < Math.min(row + 2, ROWS); i++)
for(int j = Math.max(column - 1, 0);
j < Math.min(column + 2, COLUMNS); j++)
if((i != row || j != column) && board[i][j])
total++;
if(board[row][column])
temp[row][column] = (total == 2 || total == 3); (4)
else
temp[row][column] = (total == 3); (5)
}
swap = board; (6)
board = temp;
temp = swap;| 1 | The for loop at the beginning of this segment of code runs once for
each generation we simulate. |
| 2 | The two nested for loops examine each
cell in board. |
| 3 | The two for loops nested inside of those loops do the
calculations to determine if a cell will be alive or dead in the next
generation. These inner loops start one row before the current row and
finish one row after the current row. They do the same for columns. The
Math.max() and Math.min() methods are used to keep the loops from
going out of bounds of the array. When backing up a row or a column, the
Math.max() methods make sure that we do not generate an index smaller
than 0. When going forward a row or a column, the Math.min() methods
make sure that we do not generate an index greater than ROWS - 1 or
COLUMNS - 1. |
| 4 | After these two innermost for loops have counted the total of living
cells around the cell in question, we decide the fate of the cell for
the next generation. If the cell’s alive and has exactly 2 or 3 living
neighbors, it’ll continue to live. |
| 5 | If a cell’s dead, it’ll come to life only if it has exactly 3 living neighbors. |
| 6 | After we’ve
stored the state of each cell in the next generation into temp, we
swap board and temp, using the swap variable. We could have thrown
out the old array stored in board instead of swapping it with temp,
but then we’d have to create a new array for temp each time, which
is less efficient. |
for(int i = 0; i < 100; i++) (1)
System.out.println();
for(int row = 0; row < ROWS; row++) { (2)
for(int column = 0; column < COLUMNS; column++)
if(board[row][column])
System.out.print("*");
else
System.out.print(" ");
System.out.println();
}
try { Thread.sleep(500); } (3)
catch(InterruptedException e) {}
}
}
}| 1 | The first for loop in this segment prints 100 blank lines to clear the
screen, as we explained earlier. |
| 2 | The two nested for loops print out
the state of the current generation, with a * for each living cell and
a blank space for each dead one. |
| 3 | After the output, the code sleeps for
500 milliseconds to give the effect of an animation. We’ll discuss
exceptions in general in Chapter 12 and give more
information about the Thread.sleep() method in Chapter 13. |
Although 500 milliseconds (half a second) is a long delay for animation, the scrolling effect of the screen makes the pattern of alive and dead cells hard to perceive on a terminal. Some kind of GUI (such as we discuss in Chapter 15) could provide a more pleasing way to visualize the Game of Life, but drawing arbitrary patterns on a GUI presents its own difficulties.
6.11. Concurrency: Arrays
Arrays are critical to concurrent programming in Java. In
Chapter 13, we’ll explain how to
create independent threads of execution, each of which is tied to a
Thread object. If you have a dual, quad, or higher core computer, you
might want to use two or four threads to solve a problem, but some
programs can use hundreds. How can you keep track of all those Thread
objects? In many cases, you’ll hold references to them in an array.
Arrays can also hold large lists of data. It’s common for threaded programs to share a single array which each thread reads and writes to. In this way, memory costs are kept low because there’s only one copy of all the data. In the simplest case, each thread works on some portion of the array without interacting with the rest. Even then, how do you assign parts of the array to the different threads?
We’ll assume that each element of the array needs to be processed in
some way. For example, we might want to record whether or not each
long in an array is prime or not. If you have k threads
and an array of length n where n happens to
be a multiple of k, then it’s easy: Each thread gets
exactly n/k items to work on. For example, the first
thread will work on indexes 0 through n/k - 1, the
second thread will work on indexes n/k through
2n/k - 1, and so on, with the last thread working
on indexes (k
- 1)n/k through n - 1. Not every element in the array
will require the same amount of computation, but we often assume that
they do because it can be difficult to guess which elements will take
more time to process.
What if the number of elements in the array is not a multiple of the number of threads? We still want to assign the work the work as fairly as possible. New programmers are sometimes tempted to use the same arithmetic from the case in which the threads evenly divide the length of the array: Each thread gets ⌊n/k⌋ (using integer division) elements, and we stick the last thread with the leftovers. How bad can that be?
This assignment of work can be very poorly balanced. Consider a case with 10 threads and 28 pieces of data. ⌊28/10⌋ = 2, using integer division. Thus, the first nine threads have 2 units of work to do, but the last thread is stuck with 10! Not only is this unfair; it’s inefficient. The person writing the program probably wants to minimize the total amount of time needed to finish the job. In this case, the time from when the first thread starts to when the last thread finishes is called the task’s makespan. With this division of work, the makespan is 10 units of work.

A simple way to fix this problem is to look at the value n mod k, the leftovers when you divide n by k. We want to spread those out over the first few threads. We know that any remainder will be smaller than k. If the index of the thread (starting at 0, of course) is less than the remainder, we add an extra element to its work. In this way, 28 units of work spread over 10 threads will give 3 elements to the first 8 threads and 2 elements to the rest. Using this strategy, the makespan becomes 3 units of work, a huge improvement over 10. Finding a way to spreading work across multiple threads to improve efficiency is a form of load balancing, a broad term for dividing work across computing resources.

The program below reads the length of an array and the number of threads from the user and then prints out the amount of work for each one. You should be able to adapt the ideas in it to your own multi-threaded programs in Chapter 13.
import java.util.*;
public class AssigningWork {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("How long is your array? ");
int n = in.nextInt();
System.out.print("How many threads do you have? ");
int k = in.nextInt();
int quotient = n / k;
int remainder = n % k;
int next = 0;
for(int i = 0; i < k; i++) {
int work = quotient;
if(i < remainder)
work++;
System.out.println("Thread " + i + " does " + work
+ " units of work, starting at index " + next
+ " and ending at index " + (next + work - 1));
next += work;
}
}
}6.12. Exercises
Conceptual Problems
-
Why can’t an array be used to hold an arbitrarily long list of numbers entered by a user? What are strategies that can be used to overcome this problem?
-
In future chapters, we’ll introduce a data structure called a linked list. A linked list is a homogeneous, dynamic data structure with sequential access (unlike an array, which has random access). You can instantly jump to any place in an array, but you have to step through each element of a linked list to get to the one you want, even if you know its position in the list exactly. On the other hand, inserting values into the beginning of a linked list can be done in one step, while an array would need to be resized and have its contents copied over. List some tasks for which an array would be better than a linked list and vice versa.
-
Given the following code:
double[] array1 = new double[50]; double[] array2 = new double[50]; for(int i = 0; i < array1.length; i++) { array1[i] = i + 1; array2[i] = array2.length - i; } array2 = array1; for(int i = 1; i < array1.length; i++) array1[i] = array1[i - 1] + array1[i];What is the value in
array2[array2.length - 1]after this code is executed? -
What error will be caused by the following code, and why?
String[] array = new String[100]; System.out.println(array[99].charAt(0) + " is the first letter of the last String."); -
An array of length n in Java typically takes n times the number of bytes for each element plus an additional 16 bytes of overhead. Since an
intuses 4 bytes of storage, an array of 100intelements would take 416 bytes. Consider the following three-dimensional array declaration and allocation.int[][][] data = new int[10][5][20];How many bytes are allocated for this array? Remember that the 16 byte overhead will occur repeatedly, since Java creates a three-dimensional array as an array of arrays of arrays.
-
Our original table of city distances allocates 5 · 5 = 25
intelements to store all the distances between the five cities, including repeats. How manyintelements are allocated for the triangular, ragged array version of this city distance table? If we used the normal table style, n cities would require n2intelements. How many elements would the triangular, ragged array version allocate for n cities? -
Consider the naive method of dividing an array of length n among k threads that was discussed in Section 6.11: Each thread gets ⌊n/k⌋ (rounded down because of integer division) elements, and the last thread gets any extras. What mathematical expression describes how many extra elements are allocated to the last thread? Can you come up with an example in which the last element gets all the elements? What should have happened in this case using the other, more fair scheme for assigning the data to threads?
Programming Practice
-
In Example 6.3, our code would not count
ship,as an occurrence ofshipbecause of the comma.Rewrite the code from Example 6.3 to remove punctuation from the beginning and end of a word. Use a loop that runs as long as the character at the beginning of a word is not a letter, replacing the word with a substring of itself that does not include the first character. Use a second loop to remove non-letters from the end of a word. Be careful to stop if the length of the
Stringbecomes 0, as with text that’s entirely composed of non-letters. -
In Example 6.3, we wrote a program that counts the occurrences of each word from a list within a text. If the list of words to search within is long, it can take quite some time to search through the entire list. If the list of words were sorted, we could do a trick that would allow us to search much faster. We could play a “high-low” game, searching through the list by checking the middle word in the array. If that word’s too late in the alphabet, repeat the search on the first half of the list. If it’s too early in the alphabet, repeat the search on the second half of the list. By repeatedly dividing the list in half, until you either find the word you’re looking for or narrow your search down to a single incorrect word, you can search much faster. This kind of searching is called binary search and uses around log n comparisons to find an element in a list of n items. In contrast, looking through the list one element at a time takes about n comparisons.
Rewrite the code from Example 6.3 to use binary search, after applying selection sort from Example 6.2. Although selection sort will take some extra time, you should more than make up the difference with such a fast search. To implement binary search, keep variables for the start, middle, and end of the list. Keep adjusting the three variables until the middle index has the word you are looking for or the start and end variables reach each other. Remember to use the
compareTo()method from theStringclass to compare words. -
In Example 6.4, we gave a program that finds the maximum, minimum, mean, standard deviation, and median of a list of values. Another statistic that is sometimes important is the mode, or most commonly occurring element. For example, in the list {1, 2, 3, 3, 3, 5, 6, 6, 10}, the mode is 3. Write a program that can determine the mode of a given list of
intvalues. A list can have multiple modes if more than one element occurs with maximum frequency. For our purposes, we’ll consider any list with multiple modes to have no modes. You may wish to sort the list before starting the process of counting the frequency of each value. -
We used the example of tic-tac-toe in Example 6.7 because a more complex game would have taken too much space to solve. The game of Connect Four (or the Captain’s Mistress, as it was originally called) pits two players against each other on a 6 × 7 vertical board. One player uses red checkers while the other uses black. The two players take turns dropping their checkers into columns of the board in which the checkers will drop to the lowest empty row, due to gravity. The goal of the game is to be the first to make four in a row of your color.
Implement a version of Connect Four for two human players, similar to our version of tic-tac-toe. Many of the ideas are the same, but the details are more complicated. First, a player will only choose a particular column. Your program must then find which row a checker dropped into that column will fall to. Then, the process of counting four in a row is more difficult than the three in a row of tic-tac-toe. You will need more loops to automate the process fully.
-
Once you’ve mastered the material in Chapter 15, adapt the solution to Conway’s Game of Life from Section 6.10 to display on a graphical user interface. You can use a
GridLayoutto arrange a large number ofJLabelobjects in a grid and update their background colors toColor.BLACKandColor.WHITEas needed, using thesetBackground()method. (To make these colors visible, you will also need to call thesetOpaque()method once on eachJLabelwith an argument oftrue.) The Game of Life is much more compelling with a real GUI instead of an improvised command line representation.
Experiments
-
Creating arrays with longer and longer lengths requires more processor time, since all of those elements must be initialized to some default value. Using an OS
timecommand, determine the amount of time it takes to create anintarray of length 10, 10,000, and 10,000,000. In all likelihood, the amount of time that instantiation of the array takes is a small part of the program, and you should see very little difference in those three times. However, time is not the only important resource. When you run a JVM, it has a default heap size that limits the amount of space you can use to create new objects, including arrays. When you exceed this size, your program will crash with anOutOfMemoryError. Experiment with different sizes of arrays until you can estimate the size of your heap within 5MB or so.This estimate will be very rough, since the JVM uses other memory in the background. For a more accurate picture, you can use the
Runtime.getRuntime().maxMemory()method to determine the maximum JVM memory size and theRuntime.getRuntime().totalMemory()method to determine the total JVM memory being used. -
Run the implementation of the word search program using the binary search improvement from Exercise 6.9. Use the OS
timecommand to time the difference between the regular and binary search versions of the program with a long list of words. You may see very little difference on small input, but you can easily find a list of the 1,000 most commonly used words in English on the Internet along with long, copyright free texts from Project Gutenberg. Combining these two into a single input should see a significant increase in speed for the binary search version relative to the regular version. -
Generate input files consisting of 1,000, 10,000, and 100,000 random
intvalues. Time our implementation of selection sort from Example 6.2 running on each of these input files and redirecting output to output files. What’s the behavior of the running time as the input length increases by a factor of 10? As a function of n, how many times total does the body of the innerforloop run during selection sort? Does this function closely mirror the increase in running time?
7. Simple Graphical User Interfaces
To a true artist only that face is beautiful which, quite apart from its exterior, shines with the truth within the soul.
7.1. Problem: Codon extractor
Recall from Chapter 5 that we can record DNA as a
sequence of nucleotide bases A, C, G, and T. Using this idea, we can
represent any sequence of DNA using a String made up of those four
letters such as "ATGGAAGTATTTAAATAG".
This particular sequence contains 18 bases and six codons. A codon is a three-base subsequence in DNA. Biologists are interested in dividing DNA into codons because a single codon usually maps to the production of a specific amino acid. Amino acids, in turn, are the building blocks of proteins. The DNA sequence above contains the six codons ATG, GAA, GTA, TTT, AAA, and TAG.
We want to write a program that extracts codons from DNA
sequences entered by the user. The program must detect and inform the
user of invalid DNA sequences (those containing letters other than the
four bases). If the user enters a DNA sequence whose length is not a
multiple of three, the final codon should be written with one or two
asterisks (*), representing the missing bases.
With your knowledge of String manipulation and loops, this problem
should be easy. However, we want to solve it with a graphical user
interface, not with the command line interaction we’ve emphasized in
previous chapters. That is, the input step should be done with a window
that looks similar to the following.
And the corresponding output should look very much like this.
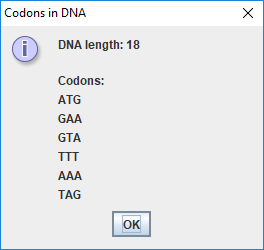
7.2. Concepts: User interaction
Many computer programs communicate with a human user. There are at least
two ways in which this communication can happen. One way is to use
command line input and output. In this case, a program prompts the user
for an input and the user responds through the keyboard, usually
completing the response by pressing the <return> or <enter> key.
Another way to communicate is to use a graphical user interface or GUI.
(Some people pronounce “GUI” to sound like “gooey,” but others say
“G-U-I.”) In this case, the program displays a window consisting of
one or more widgets, such as a button labeled “OK” or a text box in
which the user can type some text. Widgets (also known as controls) can
include buttons, labels, text areas, check boxes, menus, and many other
pre-defined objects for user interaction. While the program waits for
the user or does something in the background, the user has the option of
using a combination of the keyboard and the mouse to respond to the
program. While command line interfaces were dominant until the mid-70s,
GUIs have become the prime mode of communication between a program and a
human user. This chapter focuses on the design of simple GUIs using a
few built-in Java classes. Chapter 15 introduces more advanced tools for constructing complex
GUIs.
Figure 7.1(a) shows a Java application interacting with a user through a command line interface. The application asks the user for a temperature value in degrees Fahrenheit, converts it to the equivalent Celsius, and displays it. Figure 7.1(b) shows a similar application interacting with the user through a GUI. In this case, the application creates a window with six widgets (two labels, two text boxes, and two buttons). The user enters a temperature value in the text box below either the Celsius label or the Fahrenheit label and presses the appropriate Convert button. Then, the application displays the equivalent temperature in the other text box.

We describe the GUIs we introduce in this chapter as simple because
several aspects of GUI creation are hidden by the methods we use.
For example, these GUIs do not require the programmer to handle the
details of events such as a user pressing an “OK” button or typing
text into a text box and pressing the <enter> key. These events will
be handled automatically by existing libraries.
Chapter 15 discusses the
creation of more complex GUIs that require the programmer to program
event handling explicitly.
7.3. Syntax: Dialogs and the JOptionPane class
JOptionPane is a utility class for creating GUIs consisting
of a single dialog. It offers a variety of ways to create useful dialogs
quickly and easily and is part of the larger Java Swing GUI library. In
this chapter, we’ll show you how to use the static methods and
constants in JOptionPane to construct useful dialogs. Specifically,
you’ll learn how to construct the following four types of dialogs.
- Information
-
An information, or message, dialog displays a message to the user. Static method
showMessageDialog()creates such a dialog. See Figure 7.2 for an example of a message dialog. - Confirm
-
A confirm dialog asks a user to confirm a statement. Static method
showConfirmDialog()creates such a dialog. This dialog may return user input asYES_OPTION,NO_OPTION,OK_OPTION, orCANCEL_OPTION. See Figure 7.4 for an example of a Yes-No dialog. - Option
-
An option dialog asks the user to select one from an arbitrary set of options. Static method
showOptionDialog()creates such a dialog. See Figure 7.5 for an example. - Input
-
An input dialog is useful for obtaining data provided by the user. Static method
showInputDialog()creates such a dialog. The user can input aStringthat might represent a number, a name, or any arbitrary text. See [inputDialogFigure] for an example.
The JOptionPane class can be used to create both modal and
non-modal dialogs. A modal dialog is one that forces the user to
interact with the dialog before the program can continue. Thus, the
dialog is dismissed and the program execution resumes only after the
user has responded. Modal dialogs are useful in situations where user
input is required for the program to continue.
A non-modal dialog is one that’s displayed on the screen and doesn’t
require the user to interact with it for the underlying program to
proceed. It’s easy to create a modal dialog using the static methods in
the JOptionPane class mentioned earlier. Creation of non-modal dialogs
requires a bit more effort and is not covered in this chapter. In the
remainder of this chapter we show how to use JOptionPane to create
various types of modal dialogs.
7.3.1. Generating an information dialog
Programs often need to generate a message for the user and request a
response. The message might be a short piece of information, and the
only response might be “OK.” Alternatively, the message might be more complex and
require a more thoughtful response. In this section, we show how the
Java utility class JOptionPane can generate a simple dialog whose sole
purpose is to inform the user that a task has been completed.
Program 7.1 creates a dialog to inform the user that the task it was assigned to perform is now complete. Figure 7.2 shows the dialog generated by this program.
import javax.swing.*; (1)
public class SimpleDialog {
public static void main(String [] args) {
JOptionPane.showMessageDialog(null, (2)
"Task completed. Click OK to exit.",
"Simple Dialog", JOptionPane.INFORMATION_MESSAGE);
System.out.println("Done."); (3)
}
}| 1 | We import classes used in this program. The swing package
contains a number of classes needed to create a GUI, and JOptionPane
is one such class. |
| 2 | These lines use a static
method to create a modal dialog. JOptionPane is a utility class, and
showMessageDialog() is a static method in this class. This method,
along with the other three JOptionPane methods we discuss in this
chapter, is a factory method, meaning that it creates a new object (in
this case some kind of dialog object) on the fly with specific
attributes. In this example, the program informs the user that a
task has been completed. The method has the following four parameters.
|
| 3 | We display a message on the terminal which isn’t
needed in this program but illustrates an interesting point. When
you run SimpleDialog, you’ll notice that the "Done." message
displays on the terminal only after you’ve clicked the “OK” button.
This modal behavior blocks execution of the thread that generated it until
the button is pressed. |
In Figure 7.2 the dialog titled “Simple Dialog” includes an icon, a message, and a button labeled “OK.” This dialog is actually a frame, which is what windows are called in Java. We’ll discuss frames in greater detail in Section 15.3.

JOptionPane.The appearance of the dialog may be different on your computer. Even though Java is platform independent, GUIs are customized based on the OS you’re running. Each OS has a default look and feel (L & F) manager that specifies how widgets look and behave in your program. You can change the L & F manager, but not all managers are available on all operating systems.
In the previous example, we displayed a message of type
INFORMATION_MESSAGE. There are additional message types that could be
used.
-
ERROR_MESSAGE -
PLAIN_MESSAGE -
QUESTION_MESSAGE -
WARNING_MESSAGE
When used as parameters in showMessageDialog(), the constants above
cause different default icons to be displayed in the dialog box.
Figure 7.3 shows dialogs generated by
showMessageDialog() when using JOptionPane.ERROR_MESSAGE, (left)
and JOptionPane.WARNING_MESSAGE (right). Note the difference in the
icons displayed toward the top left of the two dialogs.
JOptionPane.ERROR_MESSAGE, and the right uses JOptionPane.WARNING_MESSAGE. The only difference is the icon displayed.7.3.2. Generating a Yes-No confirm dialog
There are situations when a program needs to obtain a binary answer from the user, a “yes” or a “no.” The next example shows how to generate such a dialog and how to get the user’s response.
Consider a program that checks whether a student understands the
difference between odd and even integers. The program generates a random
integer x, presents it to the user, and asks the question,
“Is x an odd integer?” The answer given by the user is
checked for correctness, and the user is informed accordingly.
Program 7.2 shows how to use the JOptionPane class
to generate a dialog for such an interaction.
import javax.swing.*;
import java.util.*;
public class OddEvenTest {
public static void main(String [] args) {
String title = "Odd Even Test";
Random random = new Random(); (1)
int x = random.nextInt(10);
String question = "Is " + x + " an odd integer?";
int response = JOptionPane.showConfirmDialog(null, (2)
question, title, JOptionPane.YES_NO_OPTION);
String message;
// Response is YES_OPTION for yes, NO_OPTION for no
if((response == JOptionPane.YES_OPTION && x % 2 != 0) ||
(response == JOptionPane.NO_OPTION && x % 2 == 0))
message = "You're right!";
else
message = "Sorry, that's incorrect.";
JOptionPane.showMessageDialog(null, message, title, (3)
JOptionPane.INFORMATION_MESSAGE);
}
}| 1 | We declare a random number generator named random and then use it to generate a random number from 0 to 9. |
| 2 | We present the number to the user. Note
the use of JOptionPane.YES_NO_OPTION as the last parameter in the
showConfirmDialog(). The generated
dialog is shown in Figure 7.4(a). The call to
showConfirmDialog() returns the
JOptionPane.YES_OPTION or the JOptionPane.NO_OPTION value
depending on whether the user clicked the “Yes” or “No” button. |
| 3 | A second dialog is shown with a message dependent on whether the user gives the correct answer. The two different versions of this dialog are shown in Figure 7.4(b) and (c). |

JOptionPane. (b) Dialog in response to correct answer. (c) Dialog in response to incorrect answer.Because we used YES_NO_OPTION, the dialog in
Example 7.3 automatically generates two buttons
labeled “Yes” and “No.” Dialogs can also use the
YES_NO_CANCEL_OPTION to generate a dialog with “Yes,” “No,” and
“Cancel” options. The return value from showConfirmDialog() is
CANCEL_OPTION if the user presses the “Cancel” button.
7.3.3. Generating a dialog with a list of options
The JOptionPane class can also be used to generate an arbitrary set of
options as shown in the next example.
Consider a program that asks the user to select the correct capital of a country from a list of capitals. It shows three options and asks the user to select one from among the three. It then checks the user response for correctness and displays a suitable message.
import javax.swing.*;
public class CapitalQuiz {
public static void main(String[] args) {
String title = "Capital Quiz";
String country = "Azerbaijan";
String[] capitals = {"Bujumbura","Baku", "Moroni"};
int correct = 1; //Baku is the correct answer
String question = "Select the capital of " + country + ".";
int response = JOptionPane.showOptionDialog(null, (1)
question, title, JOptionPane.PLAIN_MESSAGE,
JOptionPane.QUESTION_MESSAGE, null, capitals, null);
//Response is 0, 1, or 2 for the three options
String message;
if(response == correct)
message = "You're right!";
else
message = "Sorry, the capital of " + country +
" is " + capitals[correct] + ".";
JOptionPane.showMessageDialog(null, message, title, (2)
JOptionPane.INFORMATION_MESSAGE);
}
}| 1 | We call the showOptionDialog() method to create a dialog with multiple options. In our case, the options are three names of capitals, and only one of them is correct. Figure 7.5 shows the dialog created.The showOptionDialog() method creates an options dialog, which is the most complicated (but also the most flexible) of all the dialogs. The array of String values provided as the second to last parameter to showOptionDialog() gives the labels for the buttons.There are three null values passed into this method. The first one functions like the null used in Program 7.2, specifying that the default frame should be used. The second specifies that the default icon should be used. In the next section, we’ll show how to specify a custom icon. The last parameter indicates the default button, which will have focus when the dialog is created. If the user hits <enter> instead of clicking, the button with focus is the button that will be pressed. |
| 2 | As in Program 7.2, a second dialog is shown with a message dependent on whether the user gives the correct answer. |
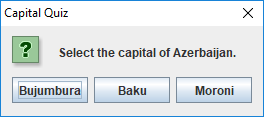
7.3.4. Generating a dialog with a custom icon
A custom icon can be included in any dialog. Each of the methods in
JOptionPane introduced earlier can take an icon as a parameter. The
next example illustrates how to do so.
Program 7.4 shows how to use
showMessageDialog() to generate a message dialog with a custom icon.
import javax.swing.*;
public class CustomIconDialog{
public static void main(String [] args){
String file = "bat.png";
String title = "Custom Icon";
String message = "Some bats eat 3,000 mosquitoes a night.";
JOptionPane.showMessageDialog(null, message, title,
JOptionPane.INFORMATION_MESSAGE, new ImageIcon(file)); (1)
}
}| 1 | The last parameter creates a new ImageIcon object from the file String ("bat.png" in this case). The resulting dialog appears in Figure 7.6. |
Dialogs illustrated in earlier examples can also use an icon parameter to include a custom icon.
Note that the icon shown above will not appear when you run this code
unless you have a copy of bat.png in the appropriate directory.
7.3.5. Generating an input dialog
An input dialog can read text data from the user. The
showInputDialog() method in the JOptionPane class allows us to
create such a dialog. We introduced the showInputDialog() method in
Section 2.3, but we give two more examples here to
emphasize its similarity to the other JOptionPane factory methods and
to show off some of its additional features.
We want to write a program that asks a question about basic chemistry. Program 7.5 shows how to display a question, obtain an answer from the user, check for the correctness of the answer, and report back to the user.
import javax.swing.*;
public class ChemistryQuizOne {
public static void main(String [] args) {
String title = "Atoms in Water";
String query = "How many atoms are in a molecule of water?";
String response = JOptionPane.showInputDialog(null, (1)
query, title, JOptionPane.QUESTION_MESSAGE);
int answer = Integer.parseInt(response); (2)
String message;
if(answer == 3) (3)
message = "You're right!";
else
message = "Sorry, that's incorrect.";
JOptionPane.showMessageDialog(null, message, title, (4)
JOptionPane.INFORMATION_MESSAGE);
}
}| 1 | We use the showInputDialog() method to generate the dialog shown in Figure 7.7. This method returns a String named response containing the text entered by the user in the dialog box. |
| 2 | We convert this String to an int and save it into variable answer. |
| 3 | We check this value against the correct answer. |
| 4 | The showMessageDialog() method informs the user whether or not the answer is correct. |
It’s important to note that the user could type any sequence of
characters in the dialog box. Try running
Program 7.5 and see what happens when you type
“two,” instead of the number “2,” into the dialog box and press the
“OK” button. The program will generate an exception indicating that
the input String cannot be converted to an integer.
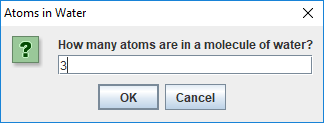
In Example 7.6 the user is required to enter text. To reduce input errors, we can restrict the user to
picking from a predefined list. We can create this list by generating an
array and supplying it as a parameter to the showInputDialog() method.
Program 7.6 displays a list of chemical elements and asks the user to select the heaviest.
import javax.swing.*;
public class ChemistryQuizTwo {
public static void main(String [] args) {
String title = "Heaviest Element";
String query = "Which is the heaviest element?";
String[] elements = {"Iron", "Uranium", "Copernicium", "Nitrogen"};
String response = (String)JOptionPane.showInputDialog(null, (1)
query, title, JOptionPane.QUESTION_MESSAGE, null, elements, null);
String message;
if(response.equals("Copernicium")) (2)
message = "You're right!";
else
message = "Sorry, correct answer: Copernicium.";
JOptionPane.showMessageDialog(null, message, title, (3)
JOptionPane.INFORMATION_MESSAGE);
}
}| 1 | We pass an array of four String values to the showInputDialog() method. Note that the last parameter to this method is null indicating that no specific item on the list should be selected by default. (In this case, the first item in the list is initially selected.) The generated dialog is shown in Figure 7.8. The four elements are contained in a drop-down list.Unlike Example 7.6, the return value from showInputDialog() is now of type Object, not of type String. The type of the list required by the method is Object array. You’re allowed to pass a String array to a method that wants an Object array due to inheritance, which is further discussed in
Chapter 11 and Chapter 17. The return value is the specific object from the array that was passed in. In our case, it has to be a String, but the compiler isn’t smart enough to figure that out. For this reason, we cast the object to a String before using the equals() method. |
| 2 | We check this String for correctness. |
| 3 | As before, the showMessageDialog() method informs the user whether or not the answer is correct. |
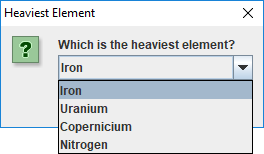
Note that this program will crash if the user clicks the “Cancel” button,
since null will be returned and stored into response.
When the number of elements in the list supplied to the
showInputDialog() is 20 or more, a JList object is automatically
used to display the items as shown in
Figure 7.9.
Other than a longer list, the code in this example is virtually identical to the code in Program 7.6.
7.4. Solution: Codon extractor
Here we give the solution to the codon extractor problem posed at the
beginning of the chapter. As we have done throughout this chapter, we
start with the import needed for GUIs built on the Swing framework. Next
we begin the CodonExtractor class and its main() method. For
readability, the solution to this problem is divided into methods that
each do a specific task. We hope that the way a method works is
intuitively clear to you. If not, the next chapter explains them in
detail.
import javax.swing.*;
public class CodonExtractor {
public static void main(String [] args) {
int continueProgram;
do { (1)
// Read DNA sequence
String input = JOptionPane.showInputDialog("Enter a DNA sequence"); (2)
input = input.toUpperCase(); (3)
String message = "Do you want to continue?";
if(isValid(input)) (4)
displayCodons(input); (5)
else
message = "Invalid DNA Sequence.\n" + message;
continueProgram = JOptionPane.showConfirmDialog((6)
null, message, "Alert", JOptionPane.YES_NO_OPTION);
} while(continueProgram == JOptionPane.YES_OPTION);
JOptionPane.showMessageDialog(null, "Thanks for using the Codon Extractor!");
}| 1 | The main() method contains a do-while loop that allows the user to
enter sequences repeatedly. |
| 2 | The showInputDialog() method makes an
input dialog and returns the String the user enters. |
| 3 | The toUpperCase() method converts the String to uppercase, allowing us to read input in either case. |
| 4 | We then call the isValid() method to make sure that the user entered a
valid DNA sequence. |
| 5 | If it is valid, we use displayCodons() to display
the codons in the sequence. |
| 6 | Either way, we use a showConfirmDialog() method to creating a confirm dialog, asking the user if he or she wants to continue entering sequences. The loop will continue as long as the return value is JOptionPane.YES_OPTION. |
public static boolean isValid(String dna) {
String validBases = "ACGT";
for(int i = 0; i < dna.length(); i++) {
char base = dna.charAt(i);
if(validBases.indexOf(base) == -1)
return false; //base not in "ACGT"
}
return true;
}The isValid() method checks to see if the DNA contains only the
letters representing the four bases. To do this, we use the Java
String library cleverly: We loop through the characters in our input,
checking to see where they can be found in "ACGT". If the index
returned is -1, the character was not found, and the DNA is invalid.
In the displayCodons() method, we display the individual codons to the
user.
public static void displayCodons(String dna) {
String message = "";
// Get as many complete codons as possible
for(int i = 0; i < dna.length() - 2; i += 3) (1)
message += "\n" + dna.substring(i, i + 3);
// 1-2 bases might be left over
int remaining = dna.length() % 3;
if(remaining == 1)
message += "\n"+ dna.substring(dna.length() - 1, dna.length()) + "**";
else if(remaining == 2)
message += "\n"+ dna.substring(dna.length() - 2, dna.length()) + "*";
message = "DNA length: " + dna.length() + "\n\nCodons: " + message;
JOptionPane.showMessageDialog(null, message, (2)
"Codons in DNA", JOptionPane.INFORMATION_MESSAGE);
}
}| 1 | We build a large String with newlines separating each codon. To do so, we loop through the input, jumping ahead three characters each time. If the input length is not a multiple of three, we pad with asterisks. |
| 2 | We use the showMessageDialog() method to display an information dialog with the list of codons. |
7.5. Concurrency: Simple GUIs
Many GUI frameworks (including Swing) are built on a multi-threaded model. Swing uses threads to redraw widgets and listen for user input while the main thread can continue processing other data.
In this chapter, the impact of these threads is minimal because we used
only modal dialogs. Every time we called a JOptionPane method, the
execution of the program’s main thread had to wait until the method
returned. As it turns out, several threads are created when
showInputDialog() or any of the others dialog methods are called, but
they do not interact with the main thread since it’s been blocked.
The situation is more complicated with a non-modal dialog, which is one of the reasons we did not go into them. In a non-modal dialog, the threads that redraw the dialog and handle its events (like a user clicking on a button) are running at the same time as the thread that created the dialog. Since many threads are running, it’s possible for them to write to the same data at the same time. Doing so can lead to inconsistencies such as the ones we’ll describe in Chapter 14.
The GUIs we’ll create in Chapter 15, however, will be more than dialogs. They will be fully functional windows, known as frames in Java. Like a non-modal dialog, the creation of a frame doesn’t block the thread that created it.
Many applications launch a frame and then end their main thread. If no other threads are created, such a program is comparatively easy to think about. However, complex applications may create multiple frames or launch threads to work on tasks in the background. Another common problem is caused by performing complicated tasks in the event handler for a GUI. If a task takes too long, the GUI can freeze or become unresponsive, as you’ve probably experienced. The fact that this problem happens so frequently even in the latest operating systems should hint at the difficulty of managing GUI threads.
When we describe how to create fully featured GUIs in Chapter 15, we’ll also give some techniques to help with avoiding unresponsive GUIs in a multi-threaded environment.
7.6. Summary
In this chapter we’ve introduced a way to create simple GUIs. These
GUIs are created using various methods available in the JOptionPane
class. While the interfaces created this way are limited in scope,
they’re often adequate for input and output in short Java programs.
Construction of more complex GUIs is the subject of
Chapter 15.
7.7. Exercises
Conceptual Problems
-
In which situations would it be better to use a command-line interface instead of a GUI? When is it better to use a GUI over a command-line interface?
-
Explain the difference between a modal and a non-modal dialog. Give an example of when you would prefer a modal over a non-modal dialog and another example of when you would prefer a non-modal to a modal dialog.
-
Give one example each when you would use the five different message type constants in
showMessageDialog()method. -
In Program 7.2, we could have coded the line checking to see if the user had correctly determined whether the number was odd or even as follows.
if((response == 0 && x % 2 != 0) || (response == 1 && x % 2 == 0))Yet another option is below.
if(response != x % 2)Which of these three implementations is best? Why?
Programming Practice
-
Modify the program in Example 7.3 such that it tests the user many times whether a randomly generated integer is odd or even. The program should keep a score indicating the number of correct answers. At the end of the test, display the score using a suitable dialog.
-
Modify the program in Example 7.3 such that it displays a dialog that asks the user “Do you wish to continue?” and offers options “Yes” and “No.” The program should exit the loop when the “No” option is selected and display the score using a suitable dialog.
-
Rewrite Program 7.2 so that the dialog generated offers the “Yes,” “No,” and “Cancel” options to the user. The program should exit with a message dialog saying “Thank You” when the user selects the “Cancel” option.
-
Modify Program 7.3 to create and administer a test wherein the user is asked capitals of 10 countries in a sequence. The program must keep a count of the number of correct answers. Inform the user of the score at the end of the test using a suitable dialog.
-
Modify Program 7.3 so that the button labeled “Baku” has focus when the program begins.
-
Section 8.5 gives a method called
shuffle()that can randomize an array representing a deck of cards. Adapt this code and modify Program 7.3 so that the order of the capitals is randomized. Note that you will need to record which index contains the correct answer. -
Re-implement the solution to the college cost calculator problem given in Section 3.5 so that it uses GUIs constructed with
JOptionPanefor input and output. -
Re-implement the solution to the Monty Hall problem given in Section 4.4 so that it uses GUIs constructed with
JOptionPanefor input and output. -
Re-implement the solution to the DNA searching problem given in Section 5.4 so that it uses GUIs constructed with
JOptionPanefor input and output. -
Write a program that creates an input dialog that prompts and reads a file name of an image from the user. Then, create an information dialog that displays the file as a custom icon. In this way, you can construct a simple image viewer.
-
Use a
try-catchblock and modify Program 7.5 so that it handles an exception generated when the user enters text that cannot be converted to an integer. In the event such an exception is raised, pop up a message dialog box informing the user to try again and type an integer value. When the user responds by clicking the “OK” button on this message box, the input dialog box should appear once again and offer the user another chance at the answer. Write two versions of the modified program. In one version, your program should give only one chance for input after an incorrect string has been typed. In another version, your program should remain in a loop until the user enters a valid integer. There is, of course, no guarantee that an answer is correct just because it’s a valid integer.Note: You should attempt this exercise only if you’re familiar with exceptions in Java. Exceptions are covered in Chapter 12.
8. Methods
Polonius (Aside): Though this be madness, yet there is method in ’t.
8.1. Problem: Three card poker
Gambling has held a fascination for humankind since its invention. As long as there have been mathematicians, they have studied the underlying mechanisms of probability and statistics that drive games of chance. A classic game of both statistics and strategy is poker. The problem we want to solve is programming one of the many variations of poker, called three card poker. Instead of bluffing, a player competes only with the house according to fixed rules without any room for psychology. A player is dealt three cards. If the player’s hand contains a pair or better, he or she wins a payoff greater than or equal to the money bet. If the player does not have a pair or better, he or she loses the money bet. Below is a table giving one possible set of payoffs for each possible hand.
| Hand | Payoff | Hand | Payoff | |
|---|---|---|---|---|
Straight Flush |
40 |
Flush |
2 |
|
Three of a Kind |
30 |
Pair |
1 |
|
Straight |
6 |
Nothing |
0 |
If you’re unfamiliar with poker rules or card games in general, here’s a quick explanation of the various hands. A traditional English or American deck of cards is made up of 52 cards, organized into four suits: spades, hearts, diamonds, and clubs. In each suit, there are 13 ranks: two, three, four, five, six, seven, eight, nine, ten, jack, queen, king, and ace.
In three card poker, a straight is when the three cards can be arranged so that their ranks (ignoring suit) are in order. For example, a hand consisting of a Four of Diamonds, a Five of Spades, and a Six of Clubs would constitute a straight. An ace can serve as either the highest rank card (coming after a king) or the lowest rank card (coming before a two) and can help form a straight in either role (but not both at the same time). A flush is when all three cards have the same suit. For example, a Three of Hearts, a Seven of Hearts, and a Jack of Hearts would constitute a flush in three card poker. A straight flush, the highest hand, is made up of cards that form both a straight (by rank ordering) and a flush (by uniformity of suit). A three of a kind occurs when all three cards have the same rank, and a pair occurs when two of the cards have the same rank. When none of these conditions hold, the hand has no special designation in three card poker, and the bet is lost.
Your task is to write a program that serves as a computerized version of the game. You must create a deck of 52 cards, thoroughly randomize them to simulate shuffling, and select the first three cards as a hand. You must then determine the highest designation that applies to the hand of cards and the corresponding winnings (if any).
Any reasonable solution to this problem uses arrays, discussed in the previous chapter. Using only that knowledge, you should be able to create a three card poker game. However, the focus of this chapter is methods, which can be used to break the solution to a problem into logical pieces. By dividing the solution in this way, we’ll be able to solve the three card poker problem in a relatively short, elegant, and easy to read way.
8.2. Concepts: Dividing work into segments
You should notice that the solutions to problems we’ve been working on have become increasingly complex as the book progresses. This progression is partly because we want to solve more interesting problems with more complex solutions but also because we’ve introduced additional Java tools that make solving these harder problems possible.
Surprisingly, the tools we introduce in this chapter do not allow you to solve a problem you couldn’t solve before. Instead, the tools in this chapter and in the next make solving a problem easier and less susceptible to errors. A relatively long, complicated list of Java statements was necessary to solve problems like the statistics program or Conway’s Game of Life. Instead of solving those problems as a single monolithic segment of code, we can break our solutions into units called static methods.
8.2.1. Reasons for static methods
A static method is a short, named segment of code that’s been packaged up so that it can be called from other parts of the program. Whenever the task performed by this method is needed, the execution of the program jumps to the code in the method, does the work it’s supposed to, and then returns to whatever it was doing before.
The reasons for using static methods can be boiled down to three essentials:
- Modularity
-
Very little software is written by individuals. Commercial software can have tens or even hundreds of developers involved in designing, implementing, testing, and maintaining code. When the code’s divided into individual methods, those methods can be written and tested by different people with minimal interference. It’s much harder to work together on one giant block of code.
- Readability
-
Methods are named segments of code. When a method is called, its name is used. If a meaningful name is chosen, the line in the code that calls the method helps document the code by explaining what’s happening. For example, if a method called
sort()is used, a reader instantly understands that something’s being sorted. If, instead of a separatesort()method, the code that does sorting was pasted into the same location, a reader might have to devote a few moments to understanding the meaning of those lines of code, particularly without comments. - Reusability
-
The fact that a method can be called from anywhere in the code makes it reusable. To use the
sort()example again, we might have to sort several different arrays in one program. Without methods, we’d have to keep copying and pasting code over and over again. With methods, the total amount of source code can be smaller. In fact, if you find yourself copying and pasting code, it’s often an indication that a method would be useful.
This idea of reusability stretches beyond individual programs. A static method can be called from an entirely different program. If you create a method that’s really useful, you’re free to use it in other programs you write. By doing so, you only have to makes changes in one place if you discover errors or want to increase its functionality.
8.2.2. Parallel to mathematical functions
We’ve been discussing the usefulness of static methods without saying exactly what they are. One way to get insight into methods is by acknowledging their similarity to functions from mathematics. In procedural (non-object oriented) languages like C, the equivalents of static methods are usually referred to as functions. Like functions in mathematics, a static method takes some number of inputs (possibly as few as zero) and usually produces some output.
You’ve already used several static methods from the Math class, such
as Math.sqrt(). Consider the following function.

This function mirrors the code inside of Math.sqrt(). In math, when you apply f(x) to
a specific value, you might write y = f(5). In Java,
you might type the following.
double y = Math.sqrt(5);In the statement f(5), the placeholder variable x takes on the value 5.
In the same way, some variable inside of
Math.sqrt() takes on the value 5 when the method is called.
It’s important to understand this similarity between methods and mathematical functions because the designers of many programming languages have been directly influenced by the older notation. However, there are many differences between the two concepts as well. Mathematical functions can take more than one input, and so can Java methods. Java methods can also take no input, while the central idea of a mathematical function is to map some input value(s) to some output value. Java methods do not necessarily even have output values. They may just do something.
8.2.3. Control flow
We have discussed selection statements such as if and switch as well
as three different looping structures, for, while, and do-while.
Each of these Java language features is used for control flow. The
selection statements allow your program to choose which code to execute.
The loops allow your code to repeatedly execute certain code. Methods
also affect control flow. When a method is called, the execution of the
program jumps into the method, does all the work it needs to there, and
then returns to the code that called it. Recall the very simple example
from above.
double y = Math.sqrt(5);The JVM has allocated a variable of type double and is preparing to
assign a value to it. Suddenly, the execution of the JVM jumps into the
code inside of the Math.sqrt() method. It takes some non-trivial
amount of work to compute the square root of a number. After that
computation is finished, the flow of execution returns to the assignment
that has been waiting all that time. Just like a mathematical function,
we can treat the method call Math.sqrt(5) as if it were “magically”
replaced by a double approximating the square root of 5.
8.3. Syntax: Methods
By now, you should have a good feel for the concepts behind calling and even creating static methods and are probably getting impatient to use them. However, we haven’t yet described all the details of Java method syntax. First, we’ll describe how you can create your own static methods, then we’ll discuss the finer points of calling static methods, and finally we’ll explain how class variables can be used from many different methods.
8.3.1. Defining methods
A very simple method that the Math class provides is the Math.max()
method. This method selects the larger of the two values provided as
input.
int maximum = Math.max(5, 10);In this case, the value stored into maximum is 10. Despite its
simplicity, we demonstrated how useful this method could be in our
solution to Conway’s Game of Life from Chapter 6. If we
wanted to write this method ourselves, the code would be as follows.
public static int max(int a, int b) {
if(a >= b)
return a;
else
return b;
}Even in such a small method, there’s a lot of syntax to
worry about. The first line of this method is called the method
header. The public keyword in this header is used to denote that any
code, even code from a different class, can call this method. We discuss
restricting access to methods and variables more in the later part of
this chapter. For now, assume that every method is public.
The keyword static indicates that this method is static. Although we
have used the term static method many times, we have not yet defined
it. A static method is linked to a whole class, not to a specific object
of that class–that is, a static method can be called without referencing
an object of the class. Again, we discuss the finer points of objects
and classes in the next chapter. For now, all methods are static.
The third keyword in the method header is the familiar int, giving the
return type of the method. Wherever this method is called, it can be
treated like an int value, because that’s what it gives back. In this
case, the return type is obvious: The maximum of two int values must
also be an int value. Any type can be used as a return value including
all the primitive types and any reference or array types. The only
limitation is that a method can only return a single item, but since
that item can be an array, this limitation is usually not important. It’s
also possible for a method to return nothing. In that case, the
keyword void is used for the return type.
Next in the method header is the identifier max, which is the name of
the method. Any legal identifier that you can use for a variable name is
valid for a method name as well. It’s important to pick a name that’s
readable and gives a reader a clear idea about what the method does. A
common convention is to name a method using a verb phrase, indicating
the operation that is being done by that method (e.g., computeTax).
Like variable names, the Java standard is to use camel notation,
starting with a lowercase letter and capitalizing the first letter of
each new word in the name.
After the name of the method is the list of parameters, separated
by commas. In this case, each parameter has the int type. You’re free
to name your parameters whatever you want, though they should be
meaningful. You can have as few as zero parameters, but there’s an
upper limit imposed by the JVM, usually 255. The body of the method
follows the header of the method, surrounded by braces ({ }). Unlike
if statements and loops, the braces for methods are required.
Inside the body of a method, the usual rules for Java control flow
apply. Each line is executed one by one unless there are selection
statements or loops. Calling methods inside of methods is also allowed. In the max() method, we use an if-else construction to find
the larger of a and b. A return statement immediately stops
execution of the method, transfers execution back to the calling code,
and gives back the value that comes after it. In this case, the value of
a is returned if it is equal or larger, and the value of b is
returned otherwise. Because a return statement immediately jumps out
of a method, we could have written the method with one fewer line of
code.
public static int max(int a, int b) {
if(a >= b)
return a;
return b;
}The only way that the line return b; can be reached is if a had not
already been returned.
Beginner programmers sometimes ask what to do if a and b are equal. In our code it’s clear that the value of a will be returned, but it hardly matters: two equal int values are indistinguishable from each other. Some students imagine handling this special case by printing an error message, but that approach is seldom useful. When trying to find the larger of two numbers in programming, it’s usually the value we want, not information about which one is actually larger.
The main() method
If some of this syntax seems eerily familiar, remember that you’ve
been coding static methods since your very first Java program. The
main() method is just another static method, special only because the
JVM chooses to start execution there. Let’s look at the main() method
from a standard Hello, World! program.
public static void main(String[] args) {
System.out.println("Hello, world!");
return;
}Just like the max() method, the header for main() starts with
public static. Then, the return type for main() is void because
the JVM is not expecting to get any answer back. The main() method has
a single parameter, an array String values. In this program, we do
not use the args parameter, but it is available. For the main()
method, this declaration is fine, because main() has to be uniform
across all programs. However, when designing your own methods, you
should not include unnecessary parameters.
The final executable line in this main() method is a return
statement. Because main() has a void return type, the return
statement has no value to return. For void methods, a return
statement is optional. You can use it to leave a method early if
desired. For a value-returning method, execution must reach a return
statement with a valid value no matter what the input of the method is.
If Java finds a way that execution could reach the end of a value
returning method without reaching a return statement, it causes a
compiler error.
Overloaded methods
Since this declaration is in another class, it’s fine to create a max()
method even though there’s already one in the Math class. However, it’s possible to create more than one method with the same name even in the
same class, provided that their signatures are not the same. Two
methods have the same signature if they have the same name and
parameter types.
public static int max(int a, int b, int c) {
return max(max(a, b), c);
}In this example, we’ve created yet another max() method, but this
one takes three parameters instead of two. This method even calls the
two parameter version of max(). Creating more than one method with the
same name is called overloading those methods. Overloading methods is
useful because it allows you to use the same method name for similar
functionality, even when there are some underlying differences in the
implementation. For example, the Math class provides four different,
overloaded versions of the max() method, specialized for int,
long, float, and double values, respectively.
There are limitations on creating overloaded methods, of course. The compiler must be able to determine which method you intend to use. Thus, the signatures have to vary by type or number of parameters. A different return type is not enough.
8.3.2. Calling methods
After a method has been defined, it must be called before it does
anything. You have plenty of experience calling static methods like
Math.sqrt() and Math.max(). An example of the appropriate syntax was
given earlier.
int maximum = Math.max(5, 10);Formally, the call starts with the name of the class (Math), followed
by a dot, followed by the name of the method (max), followed by the
list of arguments inside parentheses. These arguments are the values
you want to pass into the method. Some books use the term formal
parameters to describe the variables defined in the method signature
and actual parameters to describe the values passed into the methods,
but we stick with the simpler terms parameters and arguments.
Of course, the number of arguments must match the number of parameters
defined by the method, and the types must match as well. Java performs
automatic casting when no precision is lost. Thus, you can always supply
an int argument for a double parameter but not the reverse.
Arguments can be literal values, variables, or even other method calls
that return the appropriate type.
Using the max() method defined before, we could rewrite our simple
example without a class name.
int maximum = max(5, 10);Whenever you call a static method from code that’s inside the same class, you can leave out the class name.
Binding
Many new programmers are confused about the relationship between arguments and parameters. The process of supplying an argument to be used as a parameter is called binding. Through binding, a value or variable from the calling code is given a new name inside of a method. Consider the following method.
public static int add(int a, int b) {
return a + b;
}This absurdly short method adds two numbers together and returns the
result, approximating the functionality of the + operator. We could
call the method in the following context.
int x = 3;
int y = 5;
int z = add(x, y);Inside the method, the value of x is bound to the variable a, and
the value of y is bound to the variable b. The add() method has
its own scope. Scope means the area where a variable name is visible
(or meaningful). Thus, x and y do not exist inside of the add()
method, only the variables a and b do. Since methods have their own
scope, variables in one method can have the same names as variables in
another method without the compiler (or the programmer!) becoming
confused. Consider the following example.
int a = 3;
int b = 5;
int c = add(b, a);Here the variables a and b exist in both the calling code and inside
the method, but the names are independent. The value of a in the
calling code happens to be bound to a variable called b inside the
method, but the JVM has no confusion about which a is which. Herein
lies the value of methods: They are largely independent of whatever else
is going on in the code, allowing the programmer to focus on a small,
manageable task.
Another important feature of Java is that the process of binding variables is pass by value, meaning that only the value of the argument is bound to the parameter. Whenever a method is called, the method creates a new variable for each parameter and copies the value of its argument into it. In practice, this approach means that a method cannot directly change the value of an argument. Consider the following method.
public static void increment(int counter) {
counter++;
}This method takes the value of its argument and copies it into the new
variable counter. Then, it increments counter, but the original
argument is unchanged. Thus, the following fragment is an infinite loop.
int i = 0;
while(i < 100)
increment(i);The value of i remains fixed at 0 for the entire program. The copy
of i bound to counter increases to 1 every time increment() is
called, but i remains unaffected.
This is not to say that a method cannot affect the variables outside of
itself. The primary way that it can do so is by using return
statements. We can rewrite increment() to achieve this effect.
public static int increment(int counter) {
return counter + 1;
}Then, we need to adjust the loop so that it stores the returned value instead of dropping it on the floor.
int i = 0;
while(i < 100)
i = increment(i);A second way that methods can affect the values of outside variables is more indirect. In Java, every argument is passed by value, even arrays and objects. Practically, this means that, if a reference to an array is passed into a method, you cannot change which array it is pointing at. Since references are not values but names pointing at particular locations in memory, you can directly change the contents of that memory with a method, even if you can’t change which locations are being referenced. For example, the following method does not reverse the order of an array.
public static void badReverseArray(int[] array) {
int[] temp = new int[array.length];
for(int i = 0; i < array.length; i++)
temp[i] = array[array.length - i - 1];
array = temp;
}Although this code does store a reversed version of array in temp,
the last line of the method is meaningless: The array passed into the
method still points to the original location in memory. We can rewrite
the method to do the reversal in place, meaning that the values of the
array are shuffled around, but the array still occupies the same memory
locations.
public static void goodReverseArray(int[] array) {
int temp;
for(int i = 0; i < array.length / 2; i++) {
temp = array[i];
array[i] = array[array.length - i - 1];
array[array.length - i - 1] = temp;
}
}In this version of the method, we swap the first element of the array
with the last, the second with the second to last, and so on. We only go
up to the halfway point of the array, otherwise we would undo the reversal
process. The values of the array are reversed, but they still occupy the
same chunk of memory. It’s possible to write a correct method more in
the style of badReverseArray() which creates a temporary array, copies
the original values into it, and then copies them back to the original
array in reverse order, but it’s less efficient to create the extra
array and perform two copies.
8.3.3. Class variables
According to the rules we’ve given so far, the only legal variables in
the scope of a static method are the parameters and any other local
variables declared inside the method. However, it’s possible to create
a variable that exists outside of static methods yet is visible inside
all of them. These kinds of variables are called class variables (or
sometimes static fields or global variables). These variables
persist between method calls. The syntax for creating such a variable
is to declare it outside of all methods (but inside the class) with the keyword static and an access modifier such as public or private.
For example, the following class includes a method called record()
that increases the class variable counter every time it’s called.
record() method is called.public class Bookkeeper {
public static int counter = 0;
public static void main(String[] args) {
while(Math.random() > 0.001)
record();
System.out.println("Record was called " + counter + " times.");
}
public static void record() {
counter++;
}
}When run, this program calls the record() method some random number of
times, and the variable counter keeps track of the number. Because counter is static,
it’s accessible to both the main() and record() methods.
Many programmers frown on the use of
class variables precisely because they’re visible to many different
methods. The idea of a method is to isolate pieces of code so that the
complexity of a program can be divided into simple units. In the case of
a public class variable, even code in other classes can modify its
value. If many different pieces of code can modify a variable, it may
be difficult to keep that variable from being changed in unexpected
ways. For example, if another method used the counter variable to record the number
of times it was called, the final value of counter would be the sum of
the number of times the two methods were called. There might be some
reason to keep track of such information, but it would be impossible to
reconstruct what fraction of the value in counter came from one method
and what fraction came from the other.
Class variables have their uses, but they should generally be avoided.
The chief exception to this rule is constants. Since a constant never changes,
a class variable is a great place to store it, making the value
available to all code. An example you’ve already used is
Math.PI. As with static methods, a static field from another class can
be accessed by using the class name, then a dot, and then the name of the
static field. Again, when the code using the field is in the same class,
the class name can be dropped. A class constant is declared like a class
variable, but with the addition of the final keyword.
The following class allows a user to compute the one-dimensional force due to gravity. This force F is given by the following equation.

In this equation, m1 is the mass of one object, m2 is the mass of another, r is the distance between their centers, and G is the gravitational constant, 6.673 × 10-11 N·m2·kg-2.
import java.util.Scanner;
public class Gravity {
public static final double G = 6.673e-11;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("What is the first mass?");
double m1 = in.nextDouble();
System.out.println("What is the second mass?");
double m2 = in.nextDouble();
System.out.println("What is the distance between them?");
double r = in.nextDouble();
System.out.println("The force of gravity is " + force(m1, m2, r) + " N");
}
public static double force(double m1, double m2, double r) {
return G*m1*m2/(r*r);
}
}Use named constants whenever they increase readability. You can use the public
modifier if you want all classes to have access to your constant
(Gravity.G is a good example). You can use the private modifier if
you want the constant to be accessible only inside your class, if it has
no use outside, or if it contains secret information.
8.4. Examples: Defining methods
Any large problem should be broken down into methods. Because the
technique is useful in so many circumstances, it’s difficult to give a
set of examples that covers all cases. Instead, our examples are
short, easy to understand methods, focusing on Euclidean distance,
testing for palindromes, and converting a String representation of an
int to an int.
The Euclidean distance between two points is the length of a straight line connecting them. It plays an important role in 3D graphics and games and is the basis for many other practical applications involving spatial relationships.
Given two points in 3D space (x1, y1, z1) and (x2, y2, z2), we can compute the Euclidean distance between them with the following equation.

The method below applies this equation directly.
public static double distance(double x1, double y1, double z1,
double x2, double y2, double z2) {
double x = x1 - x2;
double y = y1 - y2;
double z = z1 - z2;
return Math.sqrt(x*x + y*y + z*z);
}This equation is a good candidate for a static method since it might be necessary to do this calculation many times and it does not depend on any other variables or program state.
A palindrome is a word or phrase (or even a number) that’s the same
spelled forward and backward. “Racecar,” “Madam, I’m Adam,” and
“Satan, oscillate my metallic sonatas” are examples in English.
Typically, spaces and punctuation are ignored. We’re going to write a
function that, given a String, returns true if it’s a palindrome
and false otherwise. To simplify the problem, we’re not going to
ignore spaces and punctuation. Thus, with our method, “racecar” counts
as a palindrome, but neither of the other two examples would.
public static boolean isPalindrome(String text) { (1)
text = text.toLowerCase(); (2)
for(int i = 0; i < text.length() / 2; i++) (3)
if(text.charAt(i) != text.charAt(text.length() - i - 1)) (4)
return false;
return true;
}| 1 | Because our method returns true or false, its return type must be
boolean. Many methods that return a boolean value have a name
starting with is, like our method. |
| 2 | The first line of the body of our
method changes text to lowercase. The String method toLowerCase()
creates a lowercase copy of the String it’s called on, in this case
text. Then, we point the reference variable text at that new,
lowercase String. On the outside of this function, the String passed in
does not change because the reference text is passed by value. |
| 3 | The loop iterates through the first half of text, comparing it to the
second half. This loop reflects the asymmetry of these kinds of tests:
You can’t be sure that text is a palindrome until you’ve checked the
entire thing, but you immediately know that it’s not if even a single
pair of characters doesn’t match. |
| 4 | If the test in that if statement
ever shows that the two char values aren’t equal, the return false
statement jumps out of the method without completing the loop. |
When you read in a number using an object of the Scanner class, it
converts (or parses) the text entered by the user into the appropriate
type. For example, the nextDouble() method reads in some text and
convert it into a double. When you use a JOptionPane method to read
in input, it comes in as a String. If you want to use that data as a
double, you must convert it using the Double.parseDouble() static
method. Some Java programmer had to write this method. We’re going to
recreate a similar method to convert the String representation of a
floating-point number into a double. Our simple method ignores
scientific notation.
public static double parseDouble(String value) {
int i = 0;
boolean negative = false;
double temp = 0.0;
double fraction = 10.0;
if(value.charAt(i) == '-') { (1)
negative = true;
i++;
}
else if(value.charAt(i) == '+')
i++;
while(i < value.length() && value.charAt(i) != '.') { (2)
temp *= 10.0;
temp += value.charAt(i) - '0';
i++;
}
i++; //move past decimal point (if there) (3)
while(i < value.length()) { (4)
temp += (value.charAt(i) - '0') / fraction;
fraction *= 10.0;
i++;
}
if(negative) (5)
temp = -temp;
return temp;
}| 1 | After declaring a few variables, this method first checks index 0 in
the input String value to see if it is a '-' or a ''`. If it is
a `'-'`, it sets `negative` to `true` and moves on. If it is a `'', it
simply moves on. |
| 2 | Then, the method loops through value until it reaches
the end or reaches a decimal point. As it iterates, it multiplies the
current value of temp by 10.0 and adds in the next digit from value
(after subtracting '0' so that the range is is from 0 to 9). This
repetitive multiplication by 10.0 accounts for the increasing powers of 10
in the base 10 number system. Since temp starts with a value of 0.0,
the first multiplication has no effect, as intended. |
| 3 | After the first while loop, the index i is incremented once, to skip
the decimal point, if there is one. If there is no decimal point, the
loop must have exited because the end of value had been reached. |
| 4 | The second while loop runs to the end of value, this time adding in each
digit value divided by fraction, which is increased by a factor of 10.0
each time. Doing so allows us to add smaller and smaller fractional
digits to the total. |
| 5 | We set temp to its opposite if the flag
negative was set earlier and finally return temp. |
Note that the real Double.parseDouble() method not only
accepts String values in scientific notation but also does a great
deal of error checking. Our code either crashes or gives inaccurate
results on an empty String, a String containing non-numerical
characters, or a String with more than one decimal point. Furthermore,
this code does not use the best approach for minimizing floating-point
precision errors.
8.5. Solution: Three card poker
Here we present our solution to the three card poker problem. We explain each method individually.
public class ThreeCardPoker {
public static final String[] SUITS = {"Spades", "Hearts", (1)
"Diamonds", "Clubs"};
public static final String[] RANKS = {"2", "3", "4", "5", "6",
"7", "8", "9", "10", "Jack", "Queen", "King", "Ace"};
public static final int STRAIGHT_FLUSH = 40; (2)
public static final int THREE_OF_A_KIND = 30;
public static final int STRAIGHT = 6;
public static final int FLUSH = 2;
public static final int PAIR = 1;
public static final int NOTHING = 0;| 1 | Before our main() method begins, we declare a number of
class constants. Two constant arrays of String values provide us with
an easy way to represent suits and ranks. |
| 2 | The remaining six int
constants are used to allocate a winning payoff to each possible
outcome. |
Note that these constants can be declared anywhere inside the class, provided that they’re outside of methods. However, it’s typical (and good style) to declare them at the top of the class.
public static void main(String[] args) {
int[] deck = new int[52]; (1)
int[] hand = new int[3];
for(int i = 0; i < deck.length; i++) (2)
deck[i] = i;
shuffle(deck);
for(int i = 0; i < hand.length; i++) (3)
hand[i] = deck[i];
int winnings = score(hand); (4)
System.out.println("Hand: ");
print(hand);
if(winnings == 0) (5)
System.out.println("You win nothing.");
else
System.out.println("You win " + winnings +
" times your bet.");
}| 1 | In the main() method, an array representing a deck of 52 cards is
created first, followed by an array representing the 3 cards to be
dealt. |
| 2 | The deck is filled sequentially and then shuffled with a method. |
| 3 | Next, the first 3 cards of the deck are copied into the array representing the hand of cards. |
| 4 | The score of the hand is determined, and then the hand is printed out. We print the hand after determining the score because the hand is sorted in the process of determining the score, making the output easier to read. |
| 5 | Finally, we print the appropriate output, depending on the score. |
public static void shuffle(int[] deck) {
int index, temp;
for(int i = 0; i < deck.length; i++) {
index = i + (int)((deck.length - i)*Math.random());
temp = deck[index];
deck[index] = deck[i];
deck[i] = temp;
}
}This method shuffles the deck. Its approach is to swap the first element
in the array of cards with one of the elements that follow, chosen
randomly. Then, it swaps the second element in the array with any of the
elements that follow it, and so on. If Math.random() truly gives us a
uniformly generated random number in the range [0,1), the
final shuffled deck should be any one of the 52! possible
decks with equal probability.
public static void print(int[] hand) { (1)
for(int i = 0; i < hand.length; i++)
System.out.println(RANKS[getRank(hand[i])] + " of "
+ SUITS[getSuit(hand[i])]);
}
public static int getRank(int value) { return value % 13; } (2)
public static int getSuit(int value) { return value / 13; } (3)| 1 | The first of these methods prints out a human readable version of each card in an array (instead of 0 - 51). It does so using the second and third methods as helper methods. |
| 2 | Method getRank() computes the rank of
a card from its number. |
| 3 | Method getSuit() computes the suit of a
card from its number. |
The indexes obtained from these methods are used
to index into the RANKS and SUITS arrays.
In the C language, calling the equivalent of a method from a method defined earlier
requires a special declaration step called prototyping before both
methods. Java does not have this complication, and the getRank() and
getSuit() methods compile and function perfectly if they are written
above print() or below it inside the class definition.
private static int score(int[] hand) {
sortByRank(hand);
if(hasStraight(hand) && hasFlush(hand))
return STRAIGHT_FLUSH;
if(hasThree(hand))
return THREE_OF_A_KIND;
if(hasStraight(hand))
return STRAIGHT;
if(hasFlush(hand))
return FLUSH;
if(hasPair(hand))
return PAIR;
return NOTHING;
} This method computes the score by first sorting the hand and then testing progressively worse outcomes, starting with the best, a straight flush. As it moves down the list of outcomes, it calls appropriate methods to determine if a hand has a certain characteristic.
private static void sortByRank(int[] hand) {
int smallest, temp;
for(int i = 0; i < hand.length - 1; i++) {
smallest = i;
for(int j = i + 1; j < hand.length; j++) {
if(getRank(hand[j]) < getRank(hand[smallest]))
smallest = j;
}
temp = hand[smallest];
hand[smallest] = hand[i];
hand[i] = temp;
}
}This code is an implementation of selection sort packaged into a method.
Note that this method does change the values inside of the
array hand even though it cannot change the array that hand points
to. The array itself is passed by value, but its contents are
effectively passed by reference.
private static boolean hasPair(int[] hand) { (1)
return getRank(hand[0]) == getRank(hand[1]) ||
getRank(hand[1]) == getRank(hand[2]);
}
private static boolean hasThree(int[] hand) { (2)
return getRank(hand[0]) == getRank(hand[1]) &&
getRank(hand[1]) == getRank(hand[2]);
}
private static boolean hasFlush(int[] hand) { (3)
return getSuit(hand[0]) == getSuit(hand[1]) &&
getSuit(hand[1]) == getSuit(hand[2]);
}
private static boolean hasStraight(int[] hand) { (4)
return (getRank(hand[0]) == 0 && getRank(hand[1]) == 1
&& getRank(hand[2]) == 12) || //ace low
(getRank(hand[1]) == getRank(hand[0]) + 1 &&
getRank(hand[2]) == getRank(hand[1]) + 1);
}
}| 1 | The code in hasPair() works by
checking to see if the first and second or second and third cards have
the same rank. An extra condition would be required if the cards weren’t sorted. |
| 2 | The code in hasThree() checks to see if all the ranks
are the same. |
| 3 | The code in hasFlush() is the same as hasThree()
except that it checks for suit instead of rank. |
| 4 | Finally, hasStraight()
checks to see if the ranks come one after the other, with an extra
case to deal with the possibility of the ace counting as low.
This test only works because the cards were sorted previously. |
These four methods would be similar but more complex for five- or seven-card poker hands.
8.6. Concurrency: Methods
In Java, it’s impossible to have concurrency without methods. Methods
are the way we break a large program into manageable pieces but are also
part of the syntax that Java uses to create threads of execution. Each
thread of execution is associated with a Thread object; however, creating
the object is not enough to start a new thread of execution running.
Only when the start() method is called on the Thread object does the
new thread start running.
Hopefully, you’ve begun to visualize the execution of Java programs as
an arrow that sits next to each line of code as it’s executed. This
arrow can jump to a choice and skip over other code using if and
switch statements. Using loops, the arrow can jump backward and
repeatedly execute code it’s just executed. As we discussed in
this chapter, the arrow can jump into a method, execute the code in that
method, and then return to its caller, going back right to where it left
off before the call.
When the start() method is called on a Thread object, however, the
arrow returns to the caller, but it also splits itself into a second
arrow that then executes the corresponding run() method and any other
methods it calls. Note that we’re talking about a method called on a
Thread object, not a static method called on the class as a whole.
Calling start() is an instance method, which we discuss in
Chapter 9. Unlike the static methods in this chapter,
an instance method is tied to a particular object, but
most of what you’ve learned about methods still applies.
Methods are supposed to make programming easier by breaking programs into chunks small enough to think about. One of the only real dangers of methods is using class variables, as mentioned in Section 8.3.3. This problem becomes worse with multiple threads. With a single thread, two or more different methods can all affect the same class variable, perhaps in conflicting ways. With multiple threads, even the same method can interfere with itself.
A linear congruential generator (LCG) allows you to create a sequence of pseudorandom numbers using the equation xi = (axi-1 + b) mod m, deriving the next number from the previous one, and so on.
rand() used in the C language.public class UnsafeRandom {
private static int next = 1;
private final static int A = 1103515245;
private final static int B = 12345;
private final static int M = 32768;
public static int nextInt() {
return next = (A*next + B) % M;
}
}The UnsafeRandom program listed above always generates the same
sequence of pseudorandom numbers, which can be useful for debugging
a program. However, if two or more threads call nextInt(), they’ll
probably get different sequences. One thread will pick up some of
the numbers, and the other will pick up the missing numbers in between. If
each thread wants to generate the same sequence of numbers, the method
should be rewritten so that it takes in the previous number in the
sequence. In that way, there’s no shared state. Remember that using a
(non-final) class variable should be avoided whenever
possible.
public class SafeRandom {
private final static int A = 1103515245;
private final static int B = 12345;
private final static int M = 32768;
public static int nextInt(int previous) {
return (A*previous + B) % M;
}
}By forcing each thread to carry its own state, we fixed the previous problem. In Chapter 14 we’ll talk about the much nastier problem of two threads executing a method at exactly the same time. When that happens, very curious effects are possible. Consider the following program.
print() method always prints "Even" when run with a single thread but can sometimes print "Odd" if called repeatedly with multiple threads.public class AlwaysEven {
private static int value = 1;
public static void print() {
value++; (1)
if(value % 2 == 0)
System.out.println("Even");
else
System.out.println("Odd");
value++; (2)
}
}| 1 | With a single thread running, value always goes up to an even number
before printing. |
| 2 | Afterward, it increments to the next odd number. |
If two or more threads call the print() method, value could
be changed by one right before the other executes the if statements.
8.7. Exercises
Conceptual Problems
-
Describe three advantages of dividing long segments of code into static methods.
-
Can you think of any disadvantages of dividing code into methods? Are there situations in which using a method is unwise?
-
If you wanted to declare a static method that would compute the mean, median, and standard deviation of an input array of
doublevalues, how would you return those three answers? -
Consider the following method definition.
public static void twice(int i) { i = 2 * i; }How many times does the following loop run, and why?
int x = 2; while(x < 128) twice(x); -
Consider the following signatures of two overloaded methods.
public static int magic(int rabbit, double hat) public static int magic(double wand, int spell)Which method would be invoked by the following call?
int x = magic(3, 16);What about the following?
int y = magic(3.2, 16.4);Use a compiler to check your answers.
-
The following class generates a sequence of even numbers. Each time the
next()method is called, the next even number in the sequence is returned. What’s the design problem with using a static field to keep track of the next value in the sequence?public class EvenNumbers { private static int counter = 0; public static int next() { counter += 2; return counter; } }
Programming Practice
-
Write a static method called
cube()that takes a singledoublevalue as a parameter and returns its value cubed. Do not use theMath.pow()method. -
Implement a static method that takes a single
intvalue as a parameter and prints its digits in reverse. For example, if103was passed into this method, it would print301to the screen.You can find out what digit is in the ones place of a number by taking its remainder modulus 10. Then, you can remove the digit in the ones place by dividing by 10. Do not convert the
intvalue into aString. -
Write a static method that takes an array of
intvalues as a parameter and returnstrueif the array is in ascending order andfalseotherwise. Compare each element of the array to the next element of the array. If the current element is ever larger than the next element, the array is not sorted in ascending order. Note that you can only be sure that the array is in ascending order after you have checked all neighboring pairs. -
Write a static method that finds the ⌊log2 n⌋ of an integer n. Note that if log2 n = x, it’s also true that n = 2x. In other words, the log2 operator tells you what power of 2 a number is. One way to define the log2 n is the number of times you have to divide n by 2 to get 1. Use this definition to make a loop that finds the value without using any calls to the
Mathlibrary.Here are some examples of the return values your method should give for various input values of n.
n Return Value n Return Value 1
0
16
4
2
1
100
6
4
2
512
9
8
3
1000
9
10
3
1024
10
-
Write a method that tests palindromes like the method from Example 8.3 but also ignores punctuation and spaces. Thus,
"A man, a plan, a canal: Panama"should be counted as a palindrome by this new method. -
Add to the
parseDouble()method from Example 8.4 so that it can also handle numbers in standard Java scientific notation, such as7.239e-14. Note that theecan be uppercase or lowercase, and the exponent can begin with a minus sign (-), a plus sign (+), or neither. -
Re-implement the solution from Section 8.5 so that it uses a GUI constructed with
JOptionPaneto display the hand and the winnings. -
Five card poker is a much more common version of poker than the three card version we discussed in Section 8.1. Using static methods, implement a two-player game of poker in which the deck is shuffled and then dealt into two hands of five cards each. Then, state which player’s hand wins. With five cards, determining which hand wins is a more complicated process. The rankings of the various possible hands from best to worst are as follows.
- Straight Flush
-
All five cards belong to the same suit and have ranks in sequential order (with either ace high or low). If two people both have straight flushes, the higher ranked one wins. If they both have the same ranks, it is a tie.
- Four of a Kind
-
Four of the five cards have the same rank. If two people have four of a kind, the higher rank set of four wins.
- Full House
-
Three of the five cards have the same rank and the other two share another rank. If two people have a full house, the higher ranked set of three wins.
- Flush
-
All five cards have the same suit. If two people have flushes, the one with the highest card wins. If the highest card is a tie, the next highest is the tie breaker, and so on. If the two flushes have exactly the same ranks, the two flushes tie.
- Straight
-
All five cards have ranks in sequential order (with either ace high or low). If two people both have straight, the higher ranked one wins. If they both have the same ranks, it is a tie.
- Three of a Kind
-
Three of the cards have the same rank. If two people have three of a kind, the higher ranked set of three wins.
- Two Pair
-
A pair of cards have the same rank and another pair of cards share another rank. If two people both have two pairs, the higher ranked pair is a tiebreaker. If the higher ranked pair is the same, the lower ranked pair is a tiebreaker. If the lower ranked pair is the same, the final unpaired card is the tiebreaker. If all the ranks of both hands match, it is a tie.
- Pair
-
A pair of cards has the same rank. If two people have pairs, the rank of the pair is a tiebreaker. If the pairs have the same rank, the remaining cards in each hand are tiebreakers, in descending rank order.
- High Card
-
If none of the other cases hold, the high card determines the value of the hand. If two people have the same highest card, the remaining cards in each hand are used as tiebreakers, in descending rank order.
Experiments
-
In terms of time, there’s a small overhead associated with calling a method and returning a value, but it’s very hard to measure. Write a program with two
intvariables,aandb, whereastarts with a value of1andbstarts with a value of2. Run aforloop 100,000,000 times. On each iteration first increase the value ofaby the value ofband then increase the value ofbbya. Time this loop withSystem.nanoTime(), and then print out the time taken and the value ofa. The value ofais not important, but the compiler will optimize away the math done withaandbunless we output the value. We recommend that you run this program repeatedly to get a sense of the average running time.Now, instead of using the
+operator to addaandb, use the following method.public static int add(int a, int b) { return a + b; }Again, run your program repeatedly with this modification. What’s the difference in running time between the version that uses a method and the version that does addition directly?
Depending on your JVM, it’s quite possible that there’s almost no difference. The JVM does a lot of optimizations including inlining, which replaces a call to a short method with the actual code inside the method.
9. Classes
Luminous beings are we, not this crude matter.
9.1. Problem: Nested expressions
How does the compiler check the Java code that you write and find errors? Parsing and type checking are involved processes that are key parts of compiler design. Compilers are some of the most complex programs of any kind, and building one is beyond the scope of the material covered in this book. However, we can get insight into some problems faced by compiler designers by considering the problem of correctly nested expressions.
There are many rules for forming correct Java code, but it’s always the
case that grouping symbols ((, ), [, ], {, }) must be correctly
nested. Ignoring other symbols, we may find a section of code that
contains the sequence ( ) [ ], but correctly written code never
contains ( [ ) ].
To be correctly nested, left and right parentheses must be balanced, left and right square brackets must be balanced, and left and right curly braces must be balanced. Furthermore, a correctly balanced set of parentheses can be nested inside of a correctly balanced set of square brackets or curly braces (and vice versa), but they cannot intersect as they do at the end of the previous paragraph. The table below shows more examples of correctly and incorrectly nested expressions.
| Correctly Nested | Incorrectly Nested |
|---|---|
( |
|
(){} |
}{ |
((abc)){x} |
( a { b ) c } |
({[z]}) |
{abc( |
({xyz})({ijk}[123]) |
{(333)888(}) |
But how can we examine an expression to see if it’s correctly nested? The key to solving this problem is the idea of a stack. A stack is a simple data structure with three operations: push, pop, and top. The data structure is meant to behave like a stack of books or cups or any other physical objects. When you use the push operation, you’re moving something to the top of the stack. When you use the pop operation, you’re taking something off the top of the stack. The top operation is used to read what’s currently at the top of the stack. In a stack, you can only read that very topmost item, as if all the other items were buried underneath it. A stack is known as a FILO (first in, last out) or a LIFO (last in, first out) data structure because, if you push a series of items onto the stack and then pop them all off the stack, they come off the stack in the reverse order from how they were added.
Armed with an understanding of the stack, it is straightforward to see if an expression is nested correctly. Scan through each character in the input and follow these steps.
-
If it’s a left parenthesis, left square bracket, or left curly brace, put it on the stack.
-
If it’s a right parenthesis, right square bracket, or right curly brace, check that the top of the stack is its matching left half. If it is, pop the left half off the stack. If it isn’t (or if the stack is empty), the grouping symbols are either unbalanced or intersecting. Print an error and quit.
-
For any character that isn’t a grouping symbol, ignore it and move on.
If you reach the end of input without an error, check to see if the stack is empty. If it is, then all of the left grouping symbols have been matched up with right grouping symbols. If not, there are left symbols left on the stack, and the expression isn’t correctly nested.
9.2. Concepts: Object-oriented programming
To solve the nested expressions problem, we can create a stack data
structure. Each element of the stack should be able to hold a char
value term from an expression, where a term is an operator, operand, or
a parenthesis (bracket or curly brace). Although we could get by using
only the static methods we introduced in the previous chapter, a better
tool can make programming easier.
We’re introducing these topics in a progression: First, all of our
programs were a series of sequential instructions inside of a main()
method. We added in selection statements and loops to solve more
difficult problems. As our programs became more complicated, we started
using additional static methods to divide the program into logical
segments. Now, we’re moving to fully object-oriented programming (OOP)
in which data as well as code can be packaged into objects that interact
with each other.
OOP has been a controversial topic, particularly in the computer science education community. The most important thing to remember is that we’re not throwing away any of the ideas we used before. We’re continuing on a path toward making code safer and more reusable. Several other chapters in this book touch on important ideas in OOP such as inheritance and polymorphism. Below, we’re going to focus on the basics, including the fundamentals of objects, encapsulation of data, and instance (non-static) methods.
9.2.1. Objects
You’ve already used objects, perhaps without realizing it. Every time
you use a String, you’re using an object. So far, we’ve created a
class every time we’ve written a program. A class is a way to organize
static methods, but a class is something more: a template for objects.
Whenever you write a class, the potential to create objects from it
exists.
For a conceptual example, you can think of Human as a class and Albert Einstein as an object (or an instance) of that class. The class defines certain characteristics that all human beings have: name, date of birth, height, and so on. Then, the object has specific values for each one of those characteristics, such as Albert Einstein, March 14, 1879, 175, and so on.

This idea of a class as a template is key because it means that an object of a given type (from a given class) can be used anywhere that’s appropriate for another object of that type. Later in the chapter, we’ll create an object that performs the work of a stack, storing a number of other objects. If we design a library of code that can manipulate or use stack objects, we should be able to use this library countless times for countless different stack objects without changing the code. This kind of code reuse is one of the main goals of OOP.
9.2.2. Encapsulation
In order to guarantee that objects can be used in many different contexts safely, the data inside of the object must be protected. Java provides access modifiers so that code without the appropriate permission can’t change or even read the data inside of an object.
This feature is called encapsulation. One programmer might write the class file defining a type of object while another or many others write code that uses those objects. The programmers who use objects written by others do not need to understand the inner workings of those objects. Instead, they can treat each object as a “black box” with a list of actions that the object can do. Each action has a certain specified input and a certain specified output, but the internal functioning of the object is hidden.
9.2.3. Instance methods
These “actions” are methods but not static ones. Static methods did
not need an object in order to be called. Regular (instance) methods
should be thought of as an action performed on (or by) a specific
object. This action could be asking a question, such as inquiring what
the name of an object of type Human is. This action could be telling the
object to change itself, as in the case of pushing something onto a
stack.
One of the broadest definitions of an object is a collection of data and methods to access that data. We call the data inside of an object its fields or instance data and the methods to access them instance methods. Static methods are used primarily to modularize large blocks of code into smaller functional units. However, instance methods are tightly coupled to the fields of an object and perform tasks that change the object or get information from it.
9.3. Syntax: Classes in Java
OOP concepts such as encapsulation may seem esoteric until you see them in practice. Remember, we just want to create some private data and then define a few carefully controlled ways that the data can be manipulated. First, we’ll describe how to declare fields, then explain how to write instance methods to manipulate that data, and finally give more details about protecting its privacy.
9.3.1. Fields
Fields in an object must be declared like any other data in Java. The
type of a field can be a primitive or reference type. Fields are
also sometimes called member variables. You declare fields just like you
would class variables, except without the static keyword. Here’s an
example with the Human class.
public class Human {
private String name;
private String DOB;
private int height; // in cm
}With this definition, a Human object has three attributes: name,
DOB, and height. Because the access modifier for each field is
private, code outside of this class can’t change or even read the
values. This class can’t do anything yet. Also, it doesn’t contain
a main() method. There’s no way to run
this class, but that’s fine. We could add a main() method, of course.
public class Human {
private String name;
private String DOB;
private int height; // in cm
public static void main(String[] args) {
name = "Albert Einstein";
DOB = "March 14, 1879";
height = 175;
}
}Now we’ve added a main() method, but our code doesn’t compile.
Since the main() method is a static method, it is not associated with
any particular object. When we tell the main() method to change the
fields, it doesn’t know what object we’re talking about. If we
actually want to use an object, we’ll have to create one.
public class Human {
private String name;
private String DOB;
private int height; //in cm
public static void main(String[] args) {
Human einstein = new Human();
einstein.name = "Albert Einstein";
einstein.DOB = "March 14, 1879";
einstein.height = 175;
}
}The above code compiles because we’ve used the new keyword to create
an object of type Human saved in a reference variable called
einstein. We can set the fields inside of a particular object using
dot notation. With static methods and static variables, we used the name
of the class followed by a dot, but for instance methods and instance
variables, we use the name of the object followed by a dot. Even
though each of these fields is private, we can access them from main()
because main() is inside the Human class. Code inside of another
class could create a new Human object, but it could not change its
fields.
This juxtaposition of static and non-static fields and methods inside of
a single class is confusing to many new Java programmers. The confusion
seems to stem from the fact that the class (such as Human) is a
template for objects but it’s also a place to house other related code,
such as static methods, including main().
Although the practice is discouraged, we mentioned in
Section 8.3.3 that class variables can be
stored in the class itself. Every object has a distinct copy of each
field, but there’s only a single copy of each class variable that they
all share. By using the keyword static, we could add a class variable
called population to our Human class, since that’s information
connected to humans as a whole, not to any individual human being.
public class Human {
private String name;
private String DOB;
private int height; // in cm
private static long population = 7714576923;
}We’re using a long to represent the world’s population since the
value is too big to fit in an int. If several Human objects
were created, they would each have their own name, DOB, and height
values, but the value for population would only be stored in the class.

9.3.2. Constructors
To create a new object, you have to invoke a constructor, a special
kind of method that can initialize the object. A constructor sets
up the values inside an object when the object’s first created. Let’s consider
a simple Rectangle class with only two fields: length and width,
both of type int.
public class Rectangle {
private int length;
private int width;One possible constructor for the class is given below.
public Rectangle(int l, int w) {
length = l;
width = w;
}This constructor lets us set the width and length when the object’s
created. To do so, code must invoke the constructor using the new
keyword.
Rectangle rectangle = new Rectangle(50, 20);This code creates a new Rectangle object, with length 50 and width 20.
Constructors are almost always public; otherwise, it would be
impossible for code outside of the Rectangle class to create a
Rectangle object. Note that the definition of the Rectangle
constructor does not have a return type. A constructor is the only kind
of method that doesn’t have a return type. It’s possible to have more
than one constructor as well, just as other methods can be overloaded.
For more information about overloaded methods, refer back to
Section 8.3.1.2.
public Rectangle(int value) {
length = value;
width = value;
}In the very same class, we could have this second constructor, allowing
us to create a square quickly and easily. All classes have constructors,
but some aren’t written explicitly. If you don’t type out a constructor
for a class, a default one is automatically created for you. The default
constructor takes no parameters and sets all the values inside the new
object to defaults such as null and 0. Once you do create a
constructor, the default one is no longer provided. Thus, since our
definition of the Rectangle class already contains two constructors,
the following line would cause a compiler error if someone tries to use
it in their code.
Rectangle defaultRectangle = new Rectangle();Another important thing to consider with all instance methods is scope. Fields are visible inside of instance methods, but they can be hidden by parameters and other local variables.
public Rectangle(int length, int width) {
length = length;
width = width;
}This version of the two parameter Rectangle constructor compiles, but
it doesn’t properly initialize the values of the fields length and
width. Instead, the parameters length and width are copied back
into themselves for no reason. The designers of Java anticipated that it
would be useful to refer to fields even in the presence of other
variables with the same name. To do so, the this keyword can be used.
Any field (or method) can be referred to by its object name, followed by
a dot, followed by the name of that field or method. Since you don’t
have a variable name to reference the object when you’re inside of it,
the this keyword acts as a reference to the object.
public Rectangle(int length, int width) {
this.length = length;
this.width = width;
}This version of the code functions correctly, since we’ve explicitly
told Java to store the argument length into the field length inside
the object pointed at by this and to do similarly for width.
9.3.3. Methods
Objects don’t really come to life until you add instance methods. With
the Rectangle class described above, any Rectangle objects created
would not be useful to other classes because it would be impossible to access their
data. Instead, we want to create a clear and usable relationship between
the fields and the methods.
There are many different kinds of methods, but two of the most important are accessors and mutators.
Accessors
We often want to read the data inside of various objects. With our
current definition of Rectangle, no code from an outside class can
find out the length or width of the rectangle we’re representing.
Accessor methods (or simply accessors) are designed for this task.
By definition, an accessor allows us to read some data or get some
information out of an object without making any changes to its fields.
Accessors can be thought of as asking the object a question. The names
of accessors often start with the word get.
public int getLength() {
return length;
}
public int getWidth() {
return width;
}Here are two accessors methods that we’d expect in the Rectangle
class. The first returns the value of length, and the second returns
the value of width. These methods only report information. They don’t
change the value of either variable. Their syntax should be
self-explanatory. Each is declared to be public so that anyone can
read the length and width of a rectangle. Both methods have a return
type of int because that’s the type used to store length and
width inside a Rectangle object. Neither method has any parameters.
Of course, an accessor doesn’t have to be so simple. An accessor could return a
value that needs to be computed from the underlying field data.
public int getArea() {
return length*width;
}
public int getPerimeter() {
return 2*length + 2*width;
}These accessors compute the area and perimeter, respectively, of the
rectangle in question, even though that data isn’t stored directly in
the Rectangle object.
Mutators
Some objects, such as String values, are immutable objects, meaning
that the data stored inside them cannot be changed after they’ve been
created with a constructor. If you’ve ever thought you were
changing a String, you were actually creating a new String with the
appropriate modifications. Most objects are mutable, however, and we use
methods called mutator methods (or simply mutators) to change their
fields.
Like accessors, mutators have no special syntax. The term is used to
describe any methods that change the data inside of an object. For the
Rectangle class, the only internal data we have is the length and
width variables. Mutators for these might look as follows.
public void setLength(int length) {
this.length = length;
}
public void setWidth(int width) {
this.width = width;
}Just as the names for many accessors begin with get, the names for
many mutators begin with set. Mutators often have a void return type
because they’re changing the object, not getting information back. Some
mutators might have a return type that gives information about an error
that occurred while trying to make a change. Note that we used the
this keyword once again to distinguish each field from the method
argument with the same name.
You may have noticed that we use the machinery of a method to both get
and set the length field, for example. Perhaps doing so seems
needlessly complex. After all, if the length variable had been
declared with the public modifier instead of the private modifier,
we could get and set its value directly, without using methods. In
response, let’s improve the mutators that set length and width.
public void setLength(int length) {
if(length > 0)
this.length = length;
}
public void setWidth(int width) {
if(width > 0)
this.width = width;
}With these better mutators, we can prevent a user from setting the
values of length and width to negative numbers or zero, values that
don’t make sense for dimensions of a rectangle. For more complicated
objects, it becomes even more important to protect the values of the
fields from malicious or mistaken users.
9.3.4. Access modifiers
Hiding data is at the heart of the Java OOP model. There are four
different levels of access that can be applied to fields and methods,
whether static or not. They are public, private, protected, and
package-private.
publicmodifier-
The
publicaccess modifier states that a variable or method can be accessed by any code, no matter what class contains it. Most methods should bepublicso that they can be used freely to interact with their object. Virtually no fields should bepublic. Constants (static or otherwise) are the most significant exception to this rule. Making constantspublicis usually not a problem since they can’t be changed by outside code anyway. In theRectangleclass, variableslengthandwidthare so simple that making thempublicis not unreasonable. If you have a field that can be changed at any time by any code to any value, you can leave that fieldpublic. privatemodifier-
This modifier states that a variable or method cannot be accessed by any code unless the code is contained in the same class. It’s important to realize that the restriction is based on the class, not on the object. Code inside any
Rectangleobject can modifyprivatevalues inside of any otherRectangleobject and the class as a whole. Most fields should beprivateso that outside code can’t modify them. Methods can beprivate, but these methods should be helper or utility methods used inside the class or object to divide up work. protectedmodifier-
This modifier states that a variable or method cannot be accessed by any code unless the code is contained in the same class, a subclass, or is in the same package. This level of access is more restrictive than
publicbut less restrictive thanprivateor default access. We discuss it further in the context of subclasses and inheritance in Chapter 11. - Package-private (no explicit modifier)
-
If you don’t type an access modifier when you declare a field or method, that field or method is not
public. Instead, it has the default or package-private access modifier applied to it. Fields or methods with this modifier can be accessed by any code that is in the same package or directory. A package is yet another layer of organization that Java provides to group classes together. When you use animportstatement, you can import an entire package of classes. There’s no keyword for this access modifier. It may be useful if you’re designing a package containing classes that must be able to access each other’s fields or methods. For now, you should always give your fields and methods an explicitpublicorprivate(or sometimesprotected) modifier.
From least restrictive to most restrictive, the modifiers are public,
protected, package-private, and private. Each additional level of
restriction removes a single category of access. All fields and methods
can be accessed by code from the same class. The following table gives
the contexts outside the class that can access a field or method marked
with each modifier.
| Modifier | Package | Subclass | Unrelated Classes |
|---|---|---|---|
|
Yes |
Yes |
Yes |
|
Yes |
Yes |
No |
Package-private |
Yes |
No |
No |
|
No |
No |
No |
Although large and complex programs are needed to see the real benefits of OOP in Java, here’s an example showing how objects can be used to make a roster of students.
We’re going to create a Student class so that we can store objects
containing student roster information. Then, we’re going to create a
client program that reads data from a user to create Student objects,
sort them by GPA, and then print them out.
public class Student {
public static final String[] YEARS = {"Freshman", "Sophomore", "Junior", "Senior"};
private String name;
private int year;
private double GPA;We start by defining the Student class. First, there’s a constant
array of String values, giving the names of each of the four years.
Next, fields in the Student class are declared to store the name, year, and GPA of
the student.
public Student(String name, int year, double GPA) {
setName(name);
setYear(year);
setGPA(GPA);
} We have one constructor for this class, which takes in a String, an
int, and a double corresponding to the name, year, and GPA of the
student. The constructor then internally uses mutator methods to store
the values into the fields. By doing so, we automatically take advantage
of the error checking in the GPA mutator.
public void setName(String name) { this.name = name; }
public void setYear(int year) { this.year = year; }
public void setGPA(double GPA) {
if(GPA >= 0 && GPA <= 4.0)
this.GPA = GPA;
else
System.out.println("Invalid GPA: " + GPA);
}These are the mutators corresponding to each of the three fields. The input for the name and year mutators aren’t checked, but the GPA mutator checks to make sure that the GPA value is in the proper range.
public String getName() { return name; };
public int getYear() { return year; };
public double getGPA() { return GPA; };
public String toString() {
return name + "\t" + YEARS[year] + "\t" + GPA;
}
}Finally, these accessors allow the user to find out the name, year, or
GPA of a given student. Every class in Java automatically has a
toString() method that’s called whenever an object is being printed
out directly. We have made this method return the information in
Student formatted as a String.
Creating the Student class is only half the battle. We must also
create client code to use it.
import java.util.*;
public class StudentRoster {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int students = in.nextInt(); (1)
Student[] roster = new Student[students]; (2)
for(int i = 0; i < roster.length; i++) { (3)
in.nextLine();
roster[i] = new Student(in.nextLine(), in.nextInt(), in.nextDouble());
}
sort(roster); (4)
for(int i = 0; i < roster.length; i++)
System.out.println(roster[i]);
}| 1 | The main() method in the StudentRoster class begins by reading in
the total number of students. |
| 2 | Next, it makes an array of type Student
of that length. |
| 3 | Then, it repeatedly reads in a name, year, and GPA,
creates a new Student object with those values, and stores it into the
array. |
| 4 | After creating all the Student objects, it sorts them with a
method call and prints them out. |
One oddity in this code is the seemingly superfluous in.nextLine() in
the first for loop. This line of code consumes a trailing newline
character from previous input. Take it out and see how quickly the
program malfunctions.
public static void sort(Student[] roster) {
for(int i = 0; i < roster.length - 1; i++) {
int smallest = i;
for(int j = i + 1; j < roster.length; j++)
if(roster[j].getGPA() < roster[smallest].getGPA())
smallest = j;
Student temp = roster[smallest];
roster[smallest] = roster[i];
roster[i] = temp;
}
}
}This sort() method is similar to others you’ve seen. It
implements selection sort in ascending order based on GPA.
If you run this program, you’ll notice that it doesn’t prompt the user for input. This version of the code is designed for redirected input from a file. A more user friendly, interactive version should prompt the user clearly.
Using OOP is not necessary to solve this problem. Instead of objects, we could have used three separate arrays holding the name, year, and GPA of each student, respectively. However, coordinating these arrays together would become tedious, particularly when sorting.
9.4. Advanced: Nested classes
Inside of a class, you can define fields and methods, but what about
other classes? Yes! Doing so creates a nested class. When you define a
class inside of an outer class, it can access fields and methods in the
outer class, even if they are marked private. Java allows a number of
different ways to define a nested class. They’re all useful, but each
is subtly different. Some nested classes are tied to a specific object
of the outer class while others are not.
9.4.1. Static nested classes
If you mark a nested class with the static keyword, you’re creating a
class whose objects are independent of any particular outer class
object. Such a class is called a static nested class. Consider the
following class definition.
public class Outer {
private int x;
private int y;
public static class Nested {
private int z;
}
}A static nested class is similar to a normal, top-level class with two
differences. First, the full name of a nested class is the name of the
outer class followed by a dot followed by the nested class name. Second,
when given an outer class object, code in a static nested class can
access and modify private (and protected) data in the outer class
object.

Static nested classes can be used when the class you need is only useful in connection with the outer class. Thus, nesting the class groups it with its outer class. We can create an instance of the nested class above as follows.
Outer.Nested nested = new Outer.Nested();Because it’s a static nested class, we don’t need an instance of type
Outer to create an instance of type Outer.Nested. If you compile
Outer.java, it will create two files, Outer.class and
Outer$Nested.class. The dollar sign ($) separates the names of each
level of nested class in the file name. It’s possible to nest classes
inside of nested classes, producing another .class file with another
dollar sign and the new class name appended.
Like members, static nested classes can be marked public, private,
protected, or package-private (no explicit modifier). These access
modifiers control which code can access or instantiate static nested
classes using the sames access rules for fields and methods.
One application for static nested classes is testing. You can write code
that tests the functionality of your outer class, fiddling with its
fields if needed. Then, because a separate .class file is created, you
can deliver only the .class file for the outer class to your customer.
Consider the Square class, similar to the Rectangle class given
earlier.
public class Square {
private int side;
public Square( int side ) {
this.side = side;
}
public int getArea() {
return side*side;
}
}We could add a static nested class called Test to Square to test
that its getArea() and getPerimeter() methods are working properly.
The final code might be as follows.
public class Square {
private int side;
public Square( int side ) {
this.side = side;
}
public int getArea() {
return side*side;
}
public static class Test {
public static void main(String[] args) {
Square square = new Square(5);
System.out.print("Test 1: ");
if(square.getArea() == 25)
System.out.println("Passed");
else
System.out.println("Failed");
square.side = 7;
System.out.print("Test 2: ");
if(square.getArea() == 49)
System.out.println("Passed");
else
System.out.println("Failed");
}
}
}To run the tests, you would compile Square.java and then run the
nested class by invoking java Square$Test. It’s unwise to use the
nested class to change the private fields in square, but we did so to
show that it’s allowed in Java. A better test would create a second
Square object with a side of length 7.
9.4.2. Inner classes
Another kind of nested class is an inner class. Unlike static nested classes, the objects of inner classes are associated with a particular object of the outer class. You can think of an inner class object living inside an outer class object. It’s impossible to instantiate an inner class object without having an outer class object first. Consider the following class definition.
public class Outer {
private int a;
public class Inner {
private int b;
private int c;
}
}Every instance of Inner must be associated with an instance of
Outer. To instantiate an inner class, you use the name of an outer
class object, followed by a dot, followed by the new keyword, and then
the name of the inner class. We can create an instance of the inner
class above as follows.
Outer outer = new Outer();
Outer.Inner inner = outer.new Inner();This syntax looks confusing, but it makes inner an object that exists
inside of outer. Thus, if there were methods defined in Inner, they
could refer to field a, because every instance of Inner would be
inside of an instance of Outer with a copy of a.
The relationship between outer and inner objects is one to many. We can instantiate any number of inner class objects that all live inside of the same outer class object.

Another issue with inner classes (as opposed to static nested classes) is that they cannot contain static methods or static fields (except for constants). Since each instance of an inner class is tied to an instance of an outer class, the designers of Java thought that static fields and methods for an inner class really belong in the outer class.
It’s even possible to define a class inside a method, if that class is only referred to in the method. Such a class is called a local class. It’s possible to create an unnamed local class on the fly as well. Such a class is called an anonymous class. Both local and anonymous classes are special kinds of inner classes. Because of the way they’re created and used, we’ll discuss them in Section 10.4
If you create a data structure for other programmers to use, a useful feature is the ability to retrieve each item from the data structure in order. Different threads or methods might need to process these elements independently from each other. Each piece of code can be given an inner class object called an iterator that can repeatedly get the next item in the data structure. Since instances of an inner class can read private data of the outer class, iterators can keep track of where they are inside of the data structure. If outside code were allowed access to the data structure’s internals, it would violate encapsulation. Iterators are a common application of inner classes.
We can create a SafeArray class that only allows data to be written to
its internal array if it falls in the legal range of indexes.
public class SafeArray {
private double[] data;
public SafeArray(int size) {
data = new double[size];
}
public int set(int index, double value) {
if(index >= 0 && index < data.length)
data[index] = value;
}
}We could add an inner class called Iterator to SafeArray that allows
us to process all the array values without knowing how many there are.
This kind of behavior is useful for many dynamic data structures, as
discussed in Chapter 18.
public class SafeArray {
private double[] data;
public SafeArray(int size) {
data = new double[size];
}
public void set(int index, double value) {
if( index >= 0 && index < data.length )
data[index] = value;
}
public class Iterator {
private int index = 0;
public boolean hasNext() {
return (index < data.length);
}
public double getNext() {
if(index >= 0 && index < data.length)
return data[index++];
else
return Double.NaN;
}
}
}The following method uses the iterator we’ve defined to find the sum
of the values in a SafeArray object.
public static findSum(SafeArray array) {
double sum = 0;
SafeArray.Iterator iterator = array.new Iterator();
while(iterator.hasNext())
sum += iterator.getNext();
return sum;
}9.5. Solution: Nested expressions
We now have enough knowledge to solve the nested expressions problem
from the beginning of the chapter. Classes help us divide up the work of
solving the problem. We need a stack class that can hold char
values. The SymbolStack class allows us to perform the push, pop, and top
stack operations with methods of the same names.
public class SymbolStack {
private char[] symbols;
private int size;
public SymbolStack(int maxSize) {
symbols = new char[maxSize]; (1)
size = 0; (2)
}
public void push( char symbol ) { symbols[size++] = symbol; } (3)
public void pop() { size--; } (4)
public char top() { return symbols[size - 1]; } (5)
public boolean isEmpty() { return size == 0; } (6)
}| 1 | Its constructor takes a maximize size for the stack and allocates an array of that size. |
| 2 | It also
sets the size field to 0 so that we can keep track of how many
things are in the stack (and consequently where the top is).
All int fields in Java are automatically initialized to 0, but it
doesn’t hurt to be explicit. |
| 3 | The push() method stores an input char into the stack at location
size and then increments size. |
| 4 | The pop() method simply decrements
size. It has no error checking to prevent a user from popping the
stack once it’s already empty. |
| 5 | The top() method returns the
value at the top of the stack, whose location is size - 1. |
| 6 | SymbolStack also defines an isEmpty() method so that we can see if
the stack is empty. |
Now we need the client code that reads the input and interacts with the stack.
import java.util.*;
public class NestedExpressions {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String input = in.nextLine(); (1)
SymbolStack stack = new SymbolStack(input.length()); (2)
char symbol;
boolean correct = true; (3)| 1 | The main() method of this class reads in the input. |
| 2 | Then, it creates a
SymbolStack called stack with a maximum size of the input length. We
know that the stack will never need to hold more than the total input length. |
| 3 | It also creates a boolean named correct to keep track of whether or not
the input is correctly nested. We start by assuming that it is. |
for(int i = 0; i < input.length() && correct; i++) { (1)
symbol = input.charAt(i);
switch(symbol) {
case '(':
case '[':
case '{':
stack.push(symbol); (2)
break;
case ')':
case ']':
case '}':
if(stack.isEmpty() || stack.top() != symbol) (3)
correct = false;
else
stack.pop();
break;
}
}| 1 | This for loop runs through each char in the input. |
| 2 | If it’s a left parenthesis, left square bracket, or left curly brace, it pushes the symbol onto the stack. |
| 3 | If it’s a right parenthesis, right square
bracket, or right curly brace, it checks to see if the stack is empty.
Because of short-circuit evaluation, the code doesn’t even look at the
top of the stack if it is empty. However, if the stack isn’t empty, it
checks to see if the top matches the current symbol. If the stack is
empty or its top doesn’t match, correct is set to false. For
efficiency, the loop stops early if correct is no longer true. |
if(!stack.isEmpty()) //unmatched left symbols (1)
correct = false;
if(correct) (2)
System.out.println("The input is correctly nested!");
else
System.out.println("The input is incorrectly nested!");
}
}| 1 | After the input has been examined, we check to see if the stack is
empty. If it isn’t, there must be some left symbols that weren’t
matched with right symbols. In that case, we set correct to false. |
| 2 | Finally, we print out whether the input is correctly or incorrectly
nested based on the value of correct. |
9.6. Concurrency: Objects
Nearly everything in Java is an object: arrays, lists, String values,
colors, and even exceptions, which form Java’s error-handling system and
are discussed in Chapter 12. Some critics of Java
point out that int, double, and the other primitive types are not
objects, forcing the programmer to adopt two different programming
models. Regardless, threads are stored as objects as well. In
Chapter 13, we’ll discuss how to create
threads and the various methods that can be used to interact with them.
However, objects of type Thread are not the only ones you deal with
when writing concurrent programs. As we’ve just noted, most data in
Java is encapsulated in an object. One of the deep reasons for using OOP
is safety: We want the private data inside of an object to stay in a
consistent state. Due to their inexplicable ability to get out of tight
spots, one tradition holds that cats have nine lives. Because of
their inquisitive nature, another tradition holds that curiosity killed
the cat. Consider the class below that keeps track of the lives a cat
has, losing one every time it becomes curious.
If the relationship between curiosity and mortality is the only feature
of a cat you’re trying to model, the class below appears to function well.
When the useCuriosity() method is invoked, it removes a life or prints
an error message if the cat has already run out of lives. In a single-threaded
situation, this object would work perfectly. No cat would be able to
lose more than 9 lives.
In a multi-threaded situation, however, there’s no telling when a thread might
pause in executing the useCuriosity() method.
Cat object starts with 9, but loses one each time it uses its curiosity. If no more lives remain, an error message is output.public class Cat {
private int lives = 9;
public boolean useCuriosity() {
if( lives > 1 ) { (1)
lives--; (2)
System.out.println("Down to life " + lives);
return true;
}
else {
System.out.println("No more lives left!");
return false;
}
}
}| 1 | If 100 threads all called useCuriosity(), each one might successfully pass the if on this line before any had decremented lives. |
| 2 | Once past the check, nothing would prevent them from continuing on and decrementing lives, resulting in a cat who lost 100 lives, resulting in a total of -91 lives. Such a scenario makes no sense. |
In Chapter 14, we’ll discuss how to prevent this
problem, using the synchronized keyword to allow only a single thread
at a time to execute a section of code. The goal is to make
useCuriosity() thread-safe, meaning that its behavior is consistent
and correct no matter how many threads try to execute it at the same
time.
As you work through this book and begin to write your own concurrent
programs, we’ll discuss many ways to make them thread-safe. However, you’re
also a consumer of code written by other people. In multi-threaded
environments, you might need to use library classes that are thread-safe.
For example, AtomicInteger is a thread-safe class designed to store
and manipulate int values. In Chapter 18,
we’ll talk about the ArrayList and Vector classes, which
are both used to hold variable length lists of objects. One of the few
differences between them is that ArrayList is not thread-safe while
Vector is. There’s even the Collections.synchronizedCollection()
method (and other similar methods), which takes a collection that’s not
thread-safe and returns a version of it that is.
Java was intended to be multi-threaded from the very beginning, but concurrency was never the most important feature in the language. For that reason, the documentation doesn’t clearly mark which methods are thread-safe. Usually, some of the paragraphs of description above the list of methods say that a class is “synchronized” if it is thread-safe. If it’s not, the documentation may not mention anything. Careful attention is needed to be sure which classes and APIs are thread-safe.
You might wonder why all classes aren’t thread-safe, but everything comes
with a price. If a class is thread-safe, its methods are usually marked
with the synchronized keyword. The JVM is relatively efficient about
how it enforces that keyword, but the computational expense is not zero.
Learn the libraries well, and use the right tools for the right job.
9.7. Exercises
Conceptual Problems
-
Explain the relationship between a class and an object.
-
What’s the difference between a static method and an instance method?
-
What’s the purpose of a constructor? Why is it impossible for a constructor to return a value? Why is it impossible for a constructor to be called multiple times on the same object?
-
A static method can be called directly from a instance method, but an instance method can’t be called directly from a static method. Why?
-
Describe the uses of accessor and mutator methods. Is it possible to create a method that is both an accessor and a mutator? Why or why not?
-
Why do we usually mark fields with the
privatekeyword when it would be easier to make all fieldspublic? -
What’s the meaning of the
thiskeyword? When is it necessary to use it? When can it be ignored? -
Consider the following class definitions.
public class A { private int a; public int getA() { return a; } public static void increment() { a++; } } public class B { private int b; public B(int value) { b = value; } public A generate() { A object = new A(); object.a = b; return object; } }The field
ais used three times in the previous code. Which of these uses cause a compiler error and why? -
In Section 9.5, we gave a definition of
SymbolStackthat implements a simple stack using two fields, as follows.private char[] symbols; private int size;By calling the
top()orpop()methods on an empty stack, it’s possible to cause a program to crash. What additional problems could happen ifsymbolsandsizewere declaredpublicand malicious or poorly written code had access to these fields? -
Consider the following class definition.
public class GroceryItem { private String name; private double price; public GroceryItem(String text, double money) { String name = text; double price = money; } public String getName() { return name; } public String getPrice() { return price; } }This class compiles, but its constructor doesn’t function properly. Why not?
Programming Practice
-
OOP is often used when the data inside the object must maintain special relationships. Consider a clock with hours, minutes, and seconds. When the number of seconds reaches 60, the number of minutes is increased by 1, and the number of seconds is reset to 0. When the number of minutes reaches 60, the number of hours is increased by 1, and the number of seconds is reset to 0. When the number of hours reaches 13, it’s reset to 1. AM and PM switch whenever the number of hours reaches 12.
Define a
Clockclass with privateintfieldshours,minutes, andsecondsand abooleanfieldPM. Write a constructor that initializeshoursto12,minutesandsecondsto0, andPMtofalse. Write a mutatorincrement()that adds1toseconds. This mutator should correctly handle all the clock behavior described above. Write an accessor calledtoString()that returns a nicely formatted version of the time as aString. For example, the initial time would be returned as"12:00:00 AM". Make sure you pad the output forsecondsandminuteswith an extra"0"if they’re less than10. -
Draw on any of your hobbies to come up with a collection of items, whether those items are books you like to read, athletes you follow, music you collect, or anything else that’s easy to classify. Then, create a class that can describe one of these items with three to five attributes. For example, the important attributes of a book might be author, title, genre, and page count. Each of these attributes should be stored as a
privatefield and manipulated withpublicaccessor and mutator methods.Using an array, create a database of these objects. Write methods that print out all objects that have a particular value for an attribute. For example, a book database program should let the user input that he or she is looking for all books whose author is
"Alexandre Dumas". You might wish to use input redirection so that you don’t have to enter data about your objects repetitively. -
The
java.awtpackage defines a class calledPointthat can be used to manipulate an (x, y) pair in programs involving the Cartesian coordinate system. Create your ownPointclass withintvaluesxandyas fields.Create one constructor that allows the user to specify values for
xandyand a default constructor that takes no arguments and sets bothxandyto0. Create accessors and mutators forxandy.Finally, create a method with the signature
public double distance(Point p)that finds the distance between the currentPointobject and thePointobjectppassed in as an argument. Recall that the following formula finds the distance d between two 2D points.Write client code that allows you to create two
Pointobjects and test if thedistance()method gives the right answer. -
Re-implement the solution from Section 9.5 so that it performs its input and output with GUIs created using
JOptionPane.
Experiments
-
Objects are great tools for solving problems, but there’s some additional overhead associated with creating objects and calling methods.
Write a piece of code that allocates an array of 10,000,000
intvalues. Iterate through that array, storing the valueiinto indexi, and time the process using an OStimecommand. As you know, theIntegerwrapper class allows us to store anintvalue in object form. Repeat the experiment, but instead ofintvalues, allocate an array to hold 10,000,000Integerobjects. Iterate through the array again, storing anIntegerobject into each index of the array. For indexi, store a newIntegerobjected created by passing valueiinto its constructor. Compare the time taken to the previous time forintvalues. Do you think this is a reasonable way to estimate the time it takes to call a constructor and allocate a new object?
10. Interfaces
Our work is the presentation of our capabilities.
10.1. Problem: Sort it out
Learning to use classes as we did in Chapter 9 provides us with useful tools. First, we can group related data together. Then, we can encapsulate that data so that it can only be changed in carefully controlled ways. But these ideas are only a fraction of the true power of object orientation available when we exploit relationships between different classes. Eventually, in Chapter 11, we’ll talk about hierarchical relationships, where one class can be the parent of many other child classes.
However, there’s a simpler relationship that classes can share, the ability to do some specific action or answer some specific question. If we know that several different classes can all do the same things, we want to be able to treat them in a unified way. For example, imagine that you’re writing code to do laboratory analysis of the free radical content of a number of creatures and items. For this analysis it’s necessary to sort the test subjects by weight and by age.
The subjects you’re going to sort will be objects of type Dog, Cat,
Person, and Cheese. All of these subjects will have some calendar
age. Naturally, the age we’re interested for a Dog is 7 times its
calendar age. At the same time, because a cat has nine lives, we’ll
use 1/9 of its calendar age. The age we use for
Person and Cheese objects is simply their calendar age.
As we discussed in Example 6.2, sorting is one of the most fundamental tools for computer scientists. In that example, we introduced selection sort. Here we’re going to use another sort called bubble sort. We introduce bubble sort to expose you to another way to sort data. Although both are easy to understand, neither bubble sort nor selection sort are the fastest ways known to sort lists.
Bubble sort works by scanning through a list of items, a pair at a time,
and swapping the elements of the pair if they’re out of order. One scan
through the list is called a pass. The algorithm keeps making passes
until no consecutive pair of elements is out of order. Here’s an
implementation of bubble sort that sorts an array of int values in
ascending order.
boolean swapped = true;
int temp;
while(swapped) {
swapped = false;
for(int i = 0; i < array.length - 1; i++)
if(array[i] > array[i + 1]) {
temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
swapped = true;
}
}|
Pitfall: Array out of bounds
Note that index variable |
The only change needed to make a bubble sort work with lists of
arbitrary objects (instead of just int values) is the if statement.
Likewise, changing the greater than (>) to a less than (<) will
change the sort from ascending to descending.
10.2. Concepts: Making a promise
Knowing how to sort a list of items is half the problem we want to solve. The other half is designing the classes so that sorting by either age or weight is easy. And easy sorting isn’t enough: We want to follow good object-oriented design so that sorting future classes will be easy as well.
For these kinds of situations, Java has a feature called interfaces. An interface is a set of methods that an object must have in order to implement that interface. If an object implements an interface, it’s making a promise to have a version of each of the methods listed in the interface. It can choose to do anything it wants inside the body of each method, but it must have them to compile. Interfaces are also described as contracts, since a contract is a promise to do certain things. One reason that interfaces are so useful is because Java allows objects to implement any number of them.
The purpose of an interface is to guarantee that an object has the capability to do something. In the case of this sorting problem, we’ll need to sort by age and weight. Consequently, the ability to report age and weight are the two important capabilities that the objects must have.
10.3. Syntax: Interfaces
Declaring an interface is similar to declaring a class except that
interfaces can only hold abstract methods, default methods, static methods,
and constants. Note that interfaces can never contain fields other than constants.
Because the purpose of an
interface is to ensure that an object has certain publicly available
capabilities, all methods and constants listed in an interface
are assumed to be public. It’s legal but clutters code to mark
interface members with public, and it’s illegal to mark them with private
or protected.
An abstract method is one that doesn’t have a body. Its return type,
name, and parameters are given, but this information is concluded with a
semicolon (;) instead of a method body.
Here’s an interface for a guitar player that defines two abstract methods.
public interface Guitarist {
void strumChord(Chord chord);
void playMelody(Melody notes);
}Any object that implements this interface must have both of these
methods, declared with the access modifier public, the same return
types, and the same parameter types. We could create a RockGuitarist class
that implements Guitarist as follows.
public class RockGuitarist implements Guitarist {
public void strumChord(Chord chord) {
System.out.print("Totally wails on that " + chord.getName() + " chord!");
}
public void playMelody(Melody notes) {
System.out.print("Burns through the notes " + notes.toString() +
" like Jimmy Page!");
}
}Or we can create a ClassicalGuitarist class. A classical guitarist is
going to approach playing a chord or a melody differently from a rock
guitarist. Java only requires that all the methods in the interface are
implemented.
public class ClassicalGuitarist implements Guitarist {
public void strumChord(Chord chord) {
System.out.print("Delicately voices a " + chord.getName() + " chord.");
}
public void playMelody(Melody notes) {
System.out.print("Plucks the melodic line " + notes.toString() +
" with the skill of John Williams.");
}
}Interfaces make our code more flexible because we can use a reference
with an interface type to refer to any objects that implement the
interface. In the following snippet of code, we do this by creating 100
Guitarist references, each of which randomly points to either a
RockGuitarist or a ClassicalGuitarist.
Guitarist[] guitarists = new Guitarist[100];
Random random = new Random();
for(int i = 0; i < guitarists.length; i++)
if(random.nextBoolean())
guitarists[i] = new RockGuitarist();
else
guitarists[i] = new ClassicalGuitarist();One benefit of using interfaces is that more mistakes can be caught at compile time instead of run time. If you implement an interface with a class you’re writing but forget (or misspell) a required method, the compiler will fail to compile that class. If you remember all of the required methods but forget to specify that your class implements a particular interface, the compiler will fail when you try to use that class in a place where that interface is required.
If you have code that takes some arbitrary object as a parameter, you
can determine if that object implements a particular interface by using
the instanceof keyword. For example, the following method takes a
Chord object and an object of type Object. The Object type is the
most basic reference type there is. All reference types in Java can be
treated as an Object type. Thus, a reference of type Object could
point at any object of any type. In this case, if the Object turns out
to implement the Guitarist interface, we can cast it to a Guitarist
and use it to strum a chord.
void checkBeforeStrum(Object unknown, Chord chord) {
if(unknown instanceof Guitarist) {
Guitarist player = (Guitarist)unknown;
player.strumChord(chord);
}
else
System.out.println("That's not a guitarist!");
}|
Pitfall: Interfaces cannot be instantiated
It’s tempting to try to create an object of an interface type. If you think about doing so carefully, it should be clear why this is impossible. An interface is only a list of promises, and it’s not a class, a template for an object. It has neither data nor methods to manipulate data. Thus, the following code will fail to compile. As we showed before, we are permitted to make a reference to an object that implements
|
10.3.1. Default methods
Before Java 8, only abstract methods (methods without bodies) could be added to interfaces. And that made sense: Interfaces were promises to do things, while classes actually did those things. Unfortunately, a problem became apparent over time. Some Java library designers would create a useful interface, and many people would write classes that implement that interface. Eventually, someone would want to add a new method to the original interface, but doing so would break lots of code. All the existing classes that implemented the interface would fail to compile until they added the new method.
To allow new methods to be added to old interfaces without breaking existing classes, the idea of a
default method was added to the rules for Java interfaces. A method with a body could be added to
an interface, provided that it was marked with the default keyword. If a class implements that interface
and has a public method that matches the default method, the class’s method will be used. However,
if a class doesn’t have a matching method, the default method will be used, and the class will still compile.
Consider the following interface similar to the original Guitarist interface except that it contains a default
tune() method.
public interface DefaultGuitarist {
void strumChord(Chord chord);
void playMelody(Melody notes);
default boolean tune() {
System.out.println("Tuning guitar...");
return true;
}
}If a class implements DefaultGuitarist and includes its own tune() method, that method will satisfy the interface.
On the other hand, a class that implements DefaultGuitarist without a tune() method will automatically include
the tune() method given above, which prints a message about tuning and then returns true (presumably indicating
that tuning was successful). The way that a class can supply a method that overrides a default method
is very similar to the way that methods can be overridden with inheritance, as discussed in Section 11.3.4.
Note that a default method must have a body.
An additional issue can arise with default methods when a class implements two or more interfaces that specify default
methods with the same signature. Consider the following interface that also has a tune() method.
public interface DefaultEngine {
void start();
int getRedline();
default boolean tune() {
System.out.println("Checking spark plugs...");
return true;
}
}By itself, this interface doesn’t cause any problems. However, when a class implements both it and DefaultGuitarist,
there can be a conflict.
public class EngineGuitarist implements DefaultGuitarist, DefaultEngine {
public void strumChord(Chord chord) {
System.out.println("Rumbles out " + chord.getName() + "!");
}
public void playMelody(Melody notes) {
System.out.println("Plays " + notes.toString() + " revving at different RPMs!");
}
public void start() {
System.out.println("*Crank*, *crank*, *vroooom!*");
}
public int getRedline() {
return 7000;
}
}This strange class is the template for an object that’s simultaneously an engine and a guitarist, implementing both
DefaultGuitarist and DefaultEngine. It has public methods for strumChord() and playMelody(), satisfying the
DefaultGuitarist interface. It also has public methods for start() and getRedline(), satisfying the DefaultEngine
interface. But it’s received two different default methods for tune(), one that tunes like a guitarist and one that
tunes like an engine. As a consequence, an EngineGuitarist object wouldn’t know which tune() to call and won’t
compile as it’s written.
You’re allowed to create classes like EngineGuitarist that implement more than one interface with the same default method,
but you need to create a tune() method inside EngineGuitarist to make clear what happens when tune() is called.
The use of default methods in interfaces is relatively rare, and situations where there are two conflicting default methods are rarer still. Even so, it’s important to understand how all the features of a language work. Note that it’s unlikely that you’ll be writing interfaces with default methods often, since their primary use is to add capabilities to existing interfaces without breaking classes that already use those interfaces.
10.3.2. Interfaces and static
When designing an interface, you can’t mark an abstract method static.
One way to think about this rule is that interfaces specify actions
(in the form of methods) that an object can do. Interfaces don’t specify
requirements for a class, such as its static methods or its class variables.
To illustrate, even with Chord and Melody defined, the following
interface fails to compile.
public interface AbstractStaticGuitarist {
void strumChord(Chord chord);
void playMelody(Melody notes);
static int getStrings();
}However, in Java 8 and higher, non-abstract static methods are allowed in interfaces. Such methods aren’t promises that objects of a class must fulfill. Instead, they’re simply utility methods that perform some task associated with the interface.
public interface StaticGuitarist {
void strumChord(Chord chord);
void playMelody(Melody notes);
static String nextNote(String note) {
char letter = note.charAt(0);
if(note.length() == 2) {
if(note.charAt(1) == 'b')
return "" + letter;
else {
switch(letter) {
case 'B':
case 'E':
return letter + "#";
case 'G':
return "A";
default:
return "" + (letter + 1);
}
}
}
else {
switch(letter) {
case 'B':
case 'E':
return "" + (letter + 1);
default:
return letter + "#";
}
}
}
}This interface includes the method nextNote(), which takes a String representation
of a note such as "D#" or "Bb" and returns a String with a representation of a
note one half step higher. The rules for musical notes are somewhat complex, so this
method is useful even when separate from any particular class that implements StaticGuitarist.
The nextNote() method would be called just like any static method, using the name
of its container StaticGuitarist followed by a dot followed by the name of the method itself.
String note = StaticGuitarist.nextNote("F");Neither fields nor class variables are allowed in interfaces, so neither static nor default
methods will ever change any data inside the interface. This is the fundamental difference
between an interface and a class: Interfaces never contain state. Even so, class constants are allowed.
Thus, we could define static final
values that might be useful to any class implementing an interface. With
Chord and Melody defined, the following interface will compile.
public interface ConstantGuitarist {
static final int MAJOR = 1;
static final int NATURAL_MINOR = 2;
static final int HARMONIC_MINOR = 3;
static final int MELODIC_MINOR = 4;
static final int CHROMATIC = 5;
static final int PENTATONIC = 6;
void strumChord(Chord chord);
void playMelody(Melody notes);
}Another source of confusion is that class variables will be both static and final by default
in an interface, even if those keywords aren’t used.
Some Java users object to the use of constants in interfaces, since the purpose of an interface is to define a list of a requirements for objects of a class rather than dealing with data values. Nevertheless, constants are allowed in interfaces, and the Java API uses them in many cases.
Interface names often include the suffix -able, for example,
Runnable, Callable, and Comparable. This suffix is typical because
it reminds us that a class implementing an interface has some specific
ability. Let’s consider an example in a supermarket in which the items
could have very little in common with each other but they all have a
price. We could define the interface Priceable as follows.
interface Priceable {
double getPrice();
}If bananas cost $0.49 a pound, we can define the Bananas class as
follows.
public class Bananas implements Priceable {
public static final double PRICE_PER_POUND = 0.49;
private double weight;
public Bananas(double weight) { this.weight = weight; }
public double getPrice() {
return weight*PRICE_PER_POUND;
}
}If eggs are $1.50 for a dozen large eggs and $1.75 for a dozen extra
large eggs, we can define the Eggs class as follows.
public class Eggs implements Priceable {
public static final double PRICE_PER_DOZEN_LARGE = 1.5;
public static final double PRICE_PER_DOZEN_EXTRA_LARGE = 1.75;
private int dozens;
private boolean extraLarge;
public Eggs(int dozens, boolean extraLarge) {
this.dozens = dozens;
this.extraLarge = extraLarge;
}
public double getPrice() {
if(extraLarge)
return dozens*PRICE_PER_DOZEN_EXTRA_LARGE;
else
return dozens*PRICE_PER_DOZEN_LARGE;
}
}Finally, if water is $0.99 a gallon, we can define the Water class as
follows.
public class Water implements Priceable {
public static final double PRICE_PER_GALLON = 0.99;
private int gallons;
public Water(int gallons) { this.gallons = gallons; }
public double getPrice() { return gallons*PRICE_PER_GALLON; }
}Each class could be much more complicated, but the code shown is all
that’s needed to implement the Priceable interface. Even though
there’s no clear relationship between bananas, eggs, and water, a shopping
cart filled with these items (and any others implementing the
Priceable interface) could easily be totaled at the register. If we
represent the shopping cart as an array of Priceable items, we could
write a simple method to total the values like so.
public static double getTotal(Priceable[] cart) {
double total = 0.0;
for(int i = 0; i < cart.length; i++)
total += cart[i].getPrice();
return total;
}Note that we can pass in Bananas, Eggs, Water, and many other
kinds of objects in a Priceable array as long as they all implement
this interface. Even though it’s impossible to create an object with an
interface type, we can make as many references to it as we want.
10.4. Advanced: Local and anonymous classes
If you haven’t read Section 9.4, you may want to look over that material to be sure you understand what nested classes and inner classes are. Recall that a normal inner class is declared inside of another class, but it’s also legal to declare a class inside of a method. Such a class is called a local class. Under some circumstances, it’s useful to create an inner class with no name, called an anonymous class.
Both kinds of classes are inner classes. They can access fields and
methods, even private ones. Like other inner classes,
they’re not allowed to declare static variables other than constants.
We bring up these special kinds of classes in this chapter because they’re
commonly used to create a class with a narrow purpose that implements a
required interface.
10.4.1. Local classes
A local class declaration looks like any other class declaration except
that it occurs within a method. The name of a local class only has
meaning inside the method where it’s defined. Because the scope of the
name is only the method, a local class cannot have access modifiers such
as public, private, or protected applied to it.
Consider the following method in which an Ellipse class is defined
locally. Recall that an ellipse (or oval) has a major (long) axis and a
minor (short) axis. The area of an ellipse is half its major axis times
half its minor axis times π. (Because the major and
minor axes of a circle are its diameter, this formula becomes
πr2 in that case.)

public static void createEllipse(double a1, double a2) {
class Ellipse {
private double axis1;
private double axis2;
public Ellipse(double axis1, double axis2) {
this.axis2 = axis2;
this.axis1 = axis1;
}
public double getArea() {
return Math.PI*0.5*axis1*0.5*axis2;
}
}
Ellipse e = new Ellipse(a1, a2);
System.out.println("The ellipse has area " + e.getArea());
}This Ellipse class cannot be referred to by any other methods. Since
an Ellipse class might be useful in other code, a top-level class
would make more sense than this local class. For that reason, local
classes are not commonly used.
However, we can make local classes more useful if they implement interfaces. Consider the following interface which can be implemented by any shape that returns its area.
public interface AreaGettable {
double getArea();
}The method below takes an array of AreaGettable objects and sums their
areas.
public static double sumAreas(AreaGettable[] shapes) {
double sum = 0.0;
for(int i = 0; i < shapes.length; i++)
sum += shapes[i].getArea();
return sum;
}If we create a local class that implements AreaGettable, we can use it
in conjunction with the sumAreas() method. In the following method, we expand
the local Ellipse class in this way and fill an array with
100 Ellipse instances, which can then be passed to sumAreas().
public static void createEllipses() {
class Ellipse implements AreaGettable {
private double axis1;
private double axis2;
public Ellipse(double axis1, double axis2) {
this.axis2 = axis2;
this.axis1 = axis1;
}
public double getArea() {
return Math.PI*0.5*axis1*0.5*axis2;
}
}
AreaGettable[] ellipses = new AreaGettable[100];
for(int i = 0; i < ellipses.length; i++)
ellipses[i] = new Ellipse(Math.random() * 25.0, Math.random() * 25.0);
double sum = sumAreas(ellipses);
System.out.println("The total area is " + sum);
}Even though the Ellipse class had the getArea() method before, the
compiler wouldn’t have allowed us to store Ellipse references in an
AreaGettable array until we marked the Ellipse class as implementing
AreaGettable. As in Example 10.1, we used
an array with an interface type.
10.4.2. Anonymous classes
This second Ellipse class is more useful since objects with its type
can be passed to other methods as an AreaGettable reference, but
declaring the class locally provides few benefits over a top-level
class. Indeed, local classes are seldom preferable to top-level classes.
Although anonymous classes behave like local classes, they can be
conveniently created at any point.
An anonymous class has no name. It’s created on the fly from some
interface or parent class and can be stored into a reference with that
type. In the following example, we modify the createEllipses() method
so that it creates an anonymous class which behaves exactly like the
Ellipse class and implements the AreaGettable interface.
public static void createEllipses() {
AreaGettable[] ellipses = new AreaGettable[100];
for(int i = 0; i < 100; i++) {
final double value1 = Math.random() * 25.0;
final double value2 = Math.random() * 25.0;
ellipses[i] = new AreaGettable() {
private double axis1 = value1;
private double axis2 = value2;
public double getArea() {
return Math.PI*0.5*axis1*0.5*axis2;
}
};
}
double sum = sumAreas(ellipses);
System.out.println("The total area is " + sum);
}The syntax for creating an anonymous class is ugly. First, you use the
new keyword followed by the name of the interface or parent class you
want to create the anonymous class from. Next, you put the arguments to
the parent class constructor inside of parentheses or leave empty
parentheses for an interface. Finally, you open a set of braces and fill
in the body for your anonymous class. When defining an anonymous class,
the entire body is crammed into a single statement, and you will often
need to complete that statement with a semicolon (;).
Anonymous classes don’t have constructors. If you need a constructor,
you will have to create a local class. Constructors usually aren’t
necessary since both local and anonymous classes can see local variables
and fields and use those to initialize values. Although any fields can
be used, local variables must be marked final (as shown above) if
their values will be used by local or anonymous classes. This
restriction prevents local variables from being changed in unpredictable ways by
methods in the local class.
It might not be easy to see why anonymous classes are useful. Both the Java API and libraries written by other programmers have many methods that require parameters whose type implements a particular interface. Without anonymous classes, you’d have to define a whole named class and instantiate it just for that method, even if you never use it again.
Using anonymous classes, you can create such an object in one step, right where you need it. This practice is commonly used for creating listeners for GUIs. A listener is an object that does the right action when a particular event happens. If you need many different listeners in one program, it can be convenient to create anonymous classes that can handle each event rather than defining many named classes which each have a single, narrow purpose. We’ll use this technique in Chapter 15.
10.5. Solution: Sort it out
It’s not difficult to move from totaling the value of items as we did in Example 10.1 to sorting them. Refer to the following class diagram as we explain our solution to the sorting problem posed at the beginning of the chapter. Dotted lines are used to show the “implements” relationship.

We’ll start with the definitions of the two interfaces we’ll use to compare objects.
public interface Ageable {
int getAge();
}public interface Weighable {
double getWeight();
}Classes implementing these two interfaces will be able to give their age
and weight independently. The next step is to create the Dog, Cat,
Person, and Cheese classes which implement them.
We’ll see in Chapter 11 that the Dog, Cat, and
Person classes could inherit from a common ancestor (such as
Creature or Mammal) which implements the Ageable and Weighable
interfaces. That design could reduce the total amount of code needed.
For now, each class will have to implement both interfaces directly.
public class Dog implements Ageable, Weighable {
private int age;
private double weight;
public Dog(int age, double weight) {
this.age = age;
this.weight = weight;
}
public int getAge() { return age*7; }
public double getWeight() { return weight; }
}public class Cat implements Ageable, Weighable {
private int age;
private double weight;
public Cat(int age, double weight) {
this.age = age;
this.weight = weight;
}
public int getAge() { return age/9; }
public double getWeight() { return weight; }
}public class Person implements Ageable, Weighable {
private int age;
private double weight;
public Person(int age, double weight) {
this.age = age;
this.weight = weight;
}
public int getAge() { return age; }
public double getWeight() { return weight; }
}public class Cheese implements Ageable, Weighable {
private int age;
private double weight;
private String type;
public Cheese(int age, double weight, String type) {
this.age = age;
this.weight = weight;
this.type = type;
}
public int getAge() { return age; }
public double getWeight() { return weight; }
public String getType() { return type; }
}With the classes in place, we can assume that client code will
instantiate some objects and perform operations on them. All that’s
necessary is to write the method that will do the sorting. We can wrap
the bubble sort code given earlier in a method body with only a few changes
to generalize the sort beyond int values.
public void sort(Object[] array, boolean age) {
boolean swapped = true;
Object temp;
while(swapped) {
swapped = false;
for(int i = 0; i < array.length - 1; i++)
if(outOfOrder(array[i], array[i + 1], age) {
temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
swapped = true;
}
}
}In this method, the boolean age is true if we’re sorting by age
and false if we’re sorting by weight. Note that the array elements and temp
have the Object type. Recall that any object can be stored in a
reference of type Object.
The only other change we needed was to replace the greater-than
comparison (>) with the outOfOrder() method, which we define below.
public boolean outOfOrder(Object o1, Object o2, boolean age) {
if(age) {
Ageable age1 = (Ageable)o1;
Ageable age2 = (Ageable)o2;
return age1.getAge() > age2.getAge();
}
else {
Weighable weight1 = (Weighable)o1;
Weighable weight2 = (Weighable)o2;
return weight1.getWeight() > weight2.getWeight();
}
}Even though we’ve designed our program for objects that implement both
the Ageable and Weighable interfaces, the compiler only sees
Object references in the array. Thus, we must cast each object to the
appropriate interface type to do the comparison. There’s a danger that
a user will pass in an array with objects which do not implement both
Ageable and Weighable, causing a ClassCastException. To allow for
universal sorting methods, the Java API defines a Comparable interface
which can be implemented by any class which requires sorting. With Java
5 and higher, the Comparable interface uses generics to be more
type-safe, but we won’t discuss how to use this interface until we
cover generics in Chapter 18.
10.6. Concurrency: Interfaces
As we discussed in Section 10.2, implementing an interface means promising to have public methods with the signatures specified in the interface definition. Making a promise seems only tangentially related to having multiple threads of execution. Indeed, interfaces and concurrency do not overlap a great deal, but there are two important areas where they affect one another.
The first is that a special interface called the Runnable interface
can be used to create new threads of execution. Runnable is a very
simple interface, containing the single signature void run(). Essentially,
any object with a run() method that takes no arguments and
returns no values can be used to create a thread of execution. Just as a
regular program has a single starting place,
the main() method, some method needs to be marked as a starting place
for additional threads. For more
information about using the Runnable interface, refer to
Section 13.4.5.
The second connection between interfaces and concurrency is more philosophical. What can you specify in an interface? The rules for interfaces in Java are relatively limited: You can require a class to have a public instance method with specific parameters and a specific return type. Java interfaces don’t allow you to require a static method.
In Chapter 14, we will discuss a key way to
make classes thread-safe by using the synchronized keyword.
Like static, Java does not allow an interface to
specify whether a method is synchronized. Thus, it’s impossible to use
an interface to guarantee that a method will be thread-safe.
As with all interface usage, this restriction cuts both ways: If you’re
designing an interface, there’s no way to guarantee that
implementing classes use synchronized methods. On the other hand, if
you’re implementing an interface, the designer may hope that your class
uses synchronized (or otherwise thread-safe) methods, but the interface
cannot force you to do so. Whenever thread-safety is an issue, make sure
you read (or write) the documentation carefully. Since there’s no way
to force programmers to use the synchronized keyword, the
documentation may be the only guide.
10.7. Exercises
Conceptual Problems
-
What’s the purpose of an interface?
-
Why implement an interface when it puts additional requirements on a class yet adds no functionality?
-
Is it legal to have methods marked
privateorprotectedin an interface? Why did the designers of Java make this choice? -
What’s the
instanceofkeyword used for? Why is it useful in the context of interfaces? -
What kind of programming error causes a
ClassCastException? -
Create an interface called
ColorWavelengthsthat only contains constants storing the wavelengths in nanometers for each of the seven colors of light, as given below.Color Wavelength (nm) Red
680
Orange
605
Yellow
580
Green
545
Blue
473
Indigo
430
Violet
415
-
Write an interface called
Clockthat specifies the functionality a clock should have. Remember that the classes that implement the clock may tell time in different ways (hourglass, water clock, mechanical movement, atomic clock), but they must share the basic functionality you specify. -
There are four compiler errors in the following interface. Name each one and explain why it’s an error.
public interface Singable { public int SOPRANO = 1; public static int ALTO = 2; public void sing(); private String chant(); public boolean hasDeepVoice() { return false; } public static boolean hasPerfectPitch(); public synchronized void tune(int frequency); } -
Consider the interface defined below.
public interface Explodable { boolean explode(double megatons); }Which of the following classes properly implement
Explodable?public class Dynamite implements Explodable { public boolean explode() { System.out.println("BOOM!"); return true; } } public class AtomicBomb implements Explodable { public boolean explode(double size) { System.out.println("A huge " + size + " megaton blast shakes the earth!"); return true; } } public class Grenade { public boolean explode(double megatons) { return true; } } public class Firecracker implements Explodable { private boolean explode(double megatons) { return (megatons < 0.0000001); } } -
Write a single class that correctly implements the following three interfaces.
public interface Laughable { boolean laugh(int times); }public interface Cryable { void cry(int tears, boolean moaning); }public interface Shoutable { void shout(double volume, String words); } -
If you’re sorting a list of items n elements long using bubble sort, what’s the minimum number of passes you’d need to be sure the list is sorted, assuming the worst possible ordering of items to start with? (Hint: Imagine the list is in backward order.) What’s the minimum number of passes if the list is already sorted?
Programming Practice
-
Add client code that randomly creates the objects needing sorting in the solution from Section 10.5. Design and include additional classes
WineandTortoisethat both implementAgeableandWeighable. AddtoString()methods to each class so that their contents can be easily output. Make sure you print out the list of objects after sorting to test your implementation. -
Refer to the sort given as a solution in Section 10.5. Add another
booleanto the parameters of the sort which specifies whether the sort is ascending or descending. Make the needed changes throughout the code to add this functionality. -
After learning about threads in Chapter 13, refer to the simple bubble sort from Section 10.1. The goal is now to parallelize the sort. Write some code which will generate an array of random
intvalues. Design your code so that you can spawn n threads. Partition the single array into n arrays and map one partition to each thread. Use your bubble sort implementation to sort each partition. Finally, merge the arrays back together, in sorted order, into one final array. For now, use just one thread (ideally the main thread) to do the merge.The merge operation is a simple idea, but it’s easy to make mistakes in its implementation. The idea is to have three indexes, one for each of the two arrays you’re merging and one for the result array. Always take the smaller (or larger, if sorting in descending order) element value from the two arrays and put it in the result. Then increment the index from the array you took the data from as well as the index of the result array. Be careful not to go beyond the end of the arrays which are being merged. An implementation of merging can be found in Example 19.8.
Experiments
-
Once you have implemented the sort in parallel from Exercise 10.14, time it against the sequential version. Try two, four, and eight different threads. Be sure to create one random array and use copies of the original array for both the parallel and sequential versions. Be careful not to sort an array that’s already sorted! Try array sizes of 1,000, 100,000, and 1,000,000. Did the performance increase? Was it as much as you expected?
11. Inheritance
Your children are not your children.
They are the sons and daughters of Life’s longing for itself.
They come through you but not from you,
And though they are with you yet they belong not to you.
11.1. Problem: Boolean circuits
In Chapter 4, we talked extensively about Boolean
algebra and how it can be applied to if statements in order to control
the flow of execution in your program. The commands that we give in
software must be executed by hardware in order to have an effect. It
shouldn’t be surprising that computer hardware is built out of digital
circuits that behave according to the same rules as Boolean logic. Each
component of these circuits is called a logic gate. There are logic
gates corresponding to all the Boolean operations you’re used to: AND,
OR, XOR, NOT, and others.
The output of an AND gate is the result of performing a logical AND on its inputs. That is, its output is true if and only if both of its inputs are true. The same correlation exists between each gate and the Boolean operator with the same name. At the level of circuitry, a 1 (or “on”) is often used to represent true, and a 0 (or “off”) is often used to represent false. Modern computer circuitry is built almost entirely out of such gates, performing addition, subtraction, and all other basic operations as complicated combinations of logic gates, where each digit of every number is a 1 or 0 determined by the circuit.
Because these circuits can become large and unwieldy, your problem is to write a Java program that will allow a user to specify the design of such a circuit and then see what its output is. The input to this program will be a text file redirected to standard input that gives the number of gates of the circuit, lists what each gate is, and then lists the connections between them.
The following is an example of input to make a circuit with six components.
6 true false AND XOR NOT OUTPUT 1 2 0 1 3 2 1 4 3 5 4
The first line specifies the total number of components. The next two
components give either true or false inputs, depending on their names.
The AND and the XOR correspond to gates of the same name which each
take two inputs. The NOT corresponds to a NOT gate with a single
input. Finally, OUTPUT 1 is the single output of this circuit that
we’re interested in. After the list of gates is a list of how they’re
connected. The line 2 0 1 specifies that the gate at index 2, which
happens to be an AND gate, has an input from the gate at index 0 and an
input from the gate at index 1. In other words, the AND gate has one
true input and one false input. The final circuit produced would look
like the following.

We’re only interested in the value of any OUTPUT gates. Thus, the program that’s simulating this circuit would print the following.
OUTPUT 1: true
There are many different ways to implement a solution to this problem.
The total number of gates is given as the first input. Thus, you can
make an array of gates. When you go to connect them, the indexes given
in the input will map naturally onto the gates in the array. But what
type should the array be? You could create a Gate class that could do
the work of any conceivable gate, but the implementation would be
awkward. All gates would have to have two inputs even if they don’t need
any. Adding different kinds of gates later (like a NAND, for example)
would mean rewriting the Gate class.
Instead, a cleaner approach to the solution is to use inheritance. In object-oriented languages like Java, inheritance is a process that allows you to create a new, specialized class from a more general, preexisting class.
We recommend the following inheritance hierarchy, in which the arrows point from each child class to its parent class.

As you can see, every class inherits from the Gate class. If your
array can be of type Gate, it will be able to hold objects of any
child of Gate. UnaryOperator, BinaryOperator, True, and False
are children of the basic Gate class. Then, Output and Not are
children of UnaryOperator since each only has a single input.
Naturally, And, Or, and Xor are children of BinaryOperator,
since they all have two inputs.
If this jumble of classes seems bewildering, don’t be discouraged. Each is very short and easy to write. We’ll explain what the inheritance relationship means and how to use it in the next few sections.
11.2. Concepts: Refining classes
Here we give a brief overview of inheritance that will give us enough information to continue onward. We’ll cover some of the deeper areas of the subject in Chapter 17.
11.2.1. Basic inheritance
The process of creating an inherited class out of an existing class is called inheriting a class, deriving a class, or simply subclassing. The class that already exists is called a parent class, base class, or superclass and the new class is called a child class, derived class, or subclass.
When you create a child class from a parent class, the child class inherits all of its fields and methods. Thus, you can use a child class object anywhere you’d use the parent class object. This relationship explains the terms superclass and subclass: Since you can treat any subclass object as if it were a superclass object, the superclass type can be thought of as a superset including all subclass objects.
The names superclass and subclass can sound misleading because the subclass can usually do more than the superclass. From that perspective, the child class has a superset of the fields and methods of its parent class. To avoid confusion, we favor the terminology of parent and child classes.
11.2.2. Adding functionality
When creating a child class, a programmer will normally add
functionality above and beyond the original parent class. Otherwise,
there’s little point in creating a child class. For example, a simple
Fish class might be able to do things like swim and feed. A child
Flounder class has the additional ability to camouflage itself.
Another child class, the Shark class, adds the ability to eat other
Fish objects.
By adding a few methods, we can create a new class with special abilities without interfering with the basic functionality of the underlying class.
11.2.3. Code reuse
Of course, a programmer who wished to program a Shark class could
simply copy and paste in all the code from the Fish class and then
make the necessary additions. In many ways the evolution of modern
programming languages has been to reduce the need for copying and
pasting.
Old mistakes are propagated with copying and pasting. When discovered, they must be fixed in several different locations. New mistakes can also be introduced by cutting and pasting. Instead, we wish to guarantee that working code from a parent class continues to work in a child class. Ideally, code from parent classes will not need to be debugged a second time when a child class is created.
Even without the issue of errors introduced by copying and pasting, the total amount of code increases. By minimizing the amount of code, issues of performance and storage can be improved, but not always. Object-oriented languages have taken criticism for low speed and high memory use due to the additional complexities of objects and inheritance, but compiler optimization, good library design, and improved JVM performance have brought Java a long way in this area.
11.3. Syntax: Inheritance in Java
In this section we discuss the mechanism for creating a child class in
Java using the extends keyword. Then, we discuss access restriction
and visibility, constructor issues, the Object class, and overriding
methods.
11.3.1. The extends keyword
In order to make a child class in Java, we use the extends keyword.
Let’s give an example using the Fish class defined below. This class
creates a basic fish that can swim, feed, and die. We can check its
color, location, and whether or not it’s alive. When it runs out of
energy, it dies.
import java.awt.*;
public class Fish {
protected Color color = Color.GRAY;
private double location = 0.0;
private double energy = 100.0;
private boolean alive = true;
public Color getColor() { return color; }
public double getLocation() { return location; }
public boolean isAlive() { return alive; }
public void swim() {
if(alive) {
location += 0.5;
energy -= 0.25;
}
if(energy <= 0.0)
die();
}
public void feed() { energy = 100.0; }
public void die() { alive = false; }
}From here we can create a child class called BoringFish that does
exactly what Fish does. To do so, we use the extends keyword after
the new class name, followed by the parent class name (in this case
Fish), followed by the body of the class.
public class BoringFish extends Fish {
}Just as we’re allowed to make an empty class, we’re allowed to make an
inherited class and add nothing, but doing so is pointless. Instead, we
can make a Flounder class that can change its color.
import java.awt.*;
public class Flounder extends Fish {
public void setColor(Color newColor) { color = newColor; }
}The Flounder class can do everything a Fish can: It can swim, feed,
and die. But we also add the ability to change color since
flounders are famous for their ability to mimic the ocean floor they
swim over. Note that the color field in the Fish class has the
protected access modifier, not private. We’ll come back to this
point.
Here’s a Shark class that extends Fish in another way, by adding
the capability of eating other Fish.
public class Shark extends Fish {
public void eat(Fish fish) {
fish.die();
feed();
}
}Here we have added an eat() method that takes another Fish object as
a parameter. First, the Fish parameter is killed; then the eat()
method calls feed(), restoring the energy of the Shark object. Note
that the Shark object is able to call the feed() method even though
it isn’t defined inside of Shark. Because it inherits from Fish, it
has a version of feed().
Single inheritance only
Particularly if you’ve programmed in C++, you might be wondering if it’s
possible to have one class inherit from multiple classes in Java.
In multiple inheritance, a single class can have many different parents.
Since C++ supports multiple inheritance, it would allow you to have a
SharkAlligatorMan class that inherits from the
Shark, Alligator, and Human classes. If you go back to the sorting
problem from Chapter 10, multiple inheritance would
allow us to solve the problem with an Age class and a Weight class
from which Dog, Cat, Person, and Cheese all inherit.
However, the designers of Java decided not to allow multiple
inheritance, perhaps for this reason: Imagine a River class with a
run() method and a Politician class with a run() method. It seems
strange to create a class which is both a river and politician, but
there is no rule in C++ which makes doing so impossible. If you did have
a RiverPolitician class which inherits from both, what would happen
when you call the run() method? How would the RiverPolitician class
know which of its parents' methods to pick? Surely, the way that a
politician runs for office is very different from the way a river runs
along its banks.
This problem is similar to the issue discussed in Section 10.3.1, where a class could implement more than one interface with the same default method; however, the problem is more severe in the case of multiple inheritance since it becomes unclear which fields inside of parent classes are being referred to, not just which methods.
If you find yourself in a situation where you want to use multiple inheritance in Java, try to reformulate your class hierarchy into one where your classes implement multiple interfaces. Recall that multiples interfaces can be implemented by a single class in Java, and like multiple inheritance, this practice allows a single class to be used in wildly different contexts.
Interfaces using extends
The extends keyword is not limited to classes. It’s possible for an
interface to extend another interface. In fact, an interface can extend
any number of other interfaces. As when a class implements multiple
interfaces, each interface in an extends list is separated by commas.
When an interface extends other interfaces, it includes all the methods
(and constants) they define. If a class implements an interface that
extends other interfaces, it must contain versions of all the methods
specified by all the interfaces. Recall the Ageable and Weighable
interfaces from Chapter 10, which specified the
getAge() and getWeight() methods, respectively. We could create an
interface that required both of these methods by extending Ageable and
Weighable.
public interface AgeableAndWeighable extends Ageable, Weighable {
}We could add additional methods to the AgeableAndWeighable interface,
but even empty it will enforce the contracts defined by both Ageable
and Weighable. It’s usually not necessary to create an interface
that extends other interfaces, since a class could implement each of the
individual interfaces. Nevertheless, it can be used as a convenience to
save typing or to create a reference type with certain guaranteed
abilities.
Note that a class can never extend an interface. Likewise, an interface cannot extend a class or implement another interface.
11.3.2. Access restriction and visibility
The Shark example above gives an example of inheritance in which the
child class only calls methods of the parent class and does not
interfere with the fields of the parent class. Generally, leaving parent
fields alone is a good thing because it protects the state of the parent
class from getting corrupted. However, it’s not always possible.
If we return to the earlier Flounder example, we had to change the
color field directly since there was no mutator to change it.
Perhaps the Fish class was poorly designed because it didn’t have a
color mutator. On the other hand, most fish cannot change their color,
so it might be good design to prevent outside code from changing the
color field with such a mutator. There are no absolute rules for
making these kinds of decisions.
We introduced access modifiers in Section 9.3.4, but inheritance
gives them new meaning. Recall that the
access modifier for the color field of Fish was protected. A field
or method with the protected modifier can be accessed by all child
classes (as well as classes in the same package). If the modifier for
color was private, the Flounder class would not be able to change
it directly.
In the Shark class, it must use mutators to change the value of its
own energy and the alive field of the fish object it eats since
they’re both marked private. It’s generally preferable to use mutator
and accessor methods whenever possible, even within the same class, so
that fields are not inadvertently corrupted.
11.3.3. Constructors
When you create a child class, you can imagine that a copy of the parent class exists inside of the child. When you create an object from a child class, how do you properly initialize the fields inside the parent class?
As we discussed in Chapter 9, every class has a
constructor, even if it’s a default one created for you. Whenever the
constructor for a child class is invoked, the constructor for the parent
class is invoked as well. If the parent class is also the child of some
other class, that grandparent class will have its constructor invoked as
well. This chain of constructors will continue, reaching all the way
back to the ultimate ancestor, Object.
When writing the constructor for a child class, the first line of it should be the call to the parent constructor. If you don’t explicitly call the parent constructor, its default (no parameter) constructor will be called. If the parent class does not have a default constructor, then leaving off an appropriate call to a parent constructor will result in a compiler error. Consider the following two classes.
public class Parent {
private String name;
public Parent(String name) { this.name = name; }
public String getName() { return name; }
}public class Child extends Parent {
public Child(String name) {
super("Baby " + name);
}
}As shown above, the super keyword is used to call the constructor of a
parent class. The Child constructor takes a name and prepends the
String "Baby " to it before passing it on to the Parent
constructor.
In a similar way, the this keyword can be used to call another
constructor in the same class, provided that a constructor to the
parent class is eventually reached. For example, we could add the
following constructor to the Child class.
public Child() {
this("Unknown");
}This second constructor will be called whenever a new Child object is
instantiated without any arguments. It will supply the String
"Unknown" to the other constructor, which will add "Baby" and pass
it on to the Parent class.
11.3.4. Overriding methods and hiding fields
Sometimes a parent method doesn’t provide all the power you want in the child class. It’s possible to override a parent method in the child class. Then, when that method is called on child objects, the new method will be called. The new method has exactly the same name and parameters. The return type must either be exactly the same or a child class of the original return type.
We can return to the Fish class example and make a new kind of fish
that never moves.
public class LazyFish extends Fish {
public void swim() {
System.out.println("I think I'll just sit here.");
}
}Whenever someone calls the swim() method on a LazyFish object, it
will announce that it’s going to sit where it is. Its location isn’t
updated, and its energy doesn’t change.
On the other hand, we could create another child class that swims twice
as fast as the original Fish.
public class FastFish extends Fish {
public void swim() {
super.swim();
super.swim();
}
}Every time swim() is called on objects of type FastFish, those
objects will call the swim() method from Fish twice. Thus, this fish
will move twice as fast (and consume twice as much energy). Because the
location and energy fields are private, we must use methods from
Fish to affect them. Note the use of the keyword super, allowing us
to specify that we want to call the swim() method from Fish and not
just call the same method from FastFish again. Using the super
keyword, we can call methods from the parent. If the parent didn’t
override a method from an ancestor class, we can still use super to
call a method from the most recent ancestor class that did implement the method.
However, Java does not allow us to skip over a parent method to call a
grandparent method if there’s an implementation in the parent class. In
other words, there’s no way to call something like a
super.super.swim() method.
Just as methods are overridden, fields are hidden. It’s perfectly legal to declare a field with the same name as a field from a parent class, but the new field will then be used instead of the old one.
public class A {
protected int a;
public int getA() { return a; }
public void setA(int value) { a = value; }
}public class B extends A {
protected int a;
public void setA(int value) { a = value; }
}Class B is a child of class A and declares a field called a,
hiding a field of the same name from A. However, which a is which
can cause some confusion. Consider the following fragment of code.
A objectA = new A();
B objectB = new B();
objectA.setA(5);
objectB.setA(10);
System.out.println("A = " + objectA.getA());
System.out.println("B = " + objectB.getA());The output of this code is:
A = 5 B = 0
Calling the setA() method on an A object sets the a field inside
of A. Calling the overridden setA() method on a B object sets the
a field inside of B, but since the getA() method hasn’t been
overridden, the a field from the A parent class part of B is
returned. Since that a field in B hasn’t been given a value, it
still has the default value of 0. Both a fields exist inside of B,
but the methods are poorly designed, leaving one field capable only of
being set and the other capable only of being retrieved.
11.3.5. The Object class
You may not have realized it, but every class you’ve created in Java uses
inheritance. To provide uniformity, the designers of Java made every
class the child (or grandchild or great-grandchild…) of a class
called Object. When you omit the extends clause in a class
definition, you’re making that class a direct child of Object.
As a consequence, all classes in Java are guaranteed to have the following methods.
| Method | Purpose |
|---|---|
|
Make a separate copy of an object. |
|
Determine if two objects are the same. |
|
Perform cleanup when an object is garbage collected. Similar to a destructor in C++. Rarely used. |
|
Find out what the class type of a given object is. |
|
Get the hash code for an object, useful for making hash tables of objects. |
|
Used for synchronization with threaded programs. More in Chapter 14. |
|
Same as previous. |
|
Get a |
|
Used with |
Java provides basic implementations for most of these, but if you want
them to work well for your object, you’ll have to override some of
them with appropriate methods. For example, the Object version of
toString() returns the virtual address of the object in JVM memory,
which is not very useful information.
Nevertheless, API classes usually have good equals() and toString()
methods. Aside from making a few useful methods available, having a
common ancestor for all classes means that you can store any object in
an Object reference. An array of type Object can hold anything,
provided that you know how to retrieve it. We discuss the finer points
of inheritance and polymorphism in Chapter 17 and
how to build lists and other data structures using Object references
in Chapter 18.
11.4. Examples: Problem solving with inheritance
Here are two extended examples showing how we can use inheritance to solve problems. First, we revisit the student roster example from Chapter 9 and then move onto an inheritance hierarchy of polygons.
The Student class we created in Example 9.1 is useful
but works only for undergraduate students. With only a few additions, we
can make it suitable for graduate students as well. First, let’s take
another look at the Student class.
public class Student {
public static final String[] YEARS = {"Freshman", "Sophomore", "Junior", "Senior"};
private String name;
private int year;
private double GPA;
public Student(String name, int year, double GPA) {
setName(name);
setYear(year);
setGPA(GPA);
}
public void setName(String name) { this.name = name; }
public void setYear(int year) { this.year = year; }
public void setGPA(double GPA) {
if(GPA >= 0 && GPA <= 4.0)
this.GPA = GPA;
else
System.out.println("Invalid GPA: " + GPA);
}
public String getName() { return name; };
public int getYear() { return year; };
public double getGPA() { return GPA; };
public String toString() {
return name + "\t" + YEARS[year] + "\t" + GPA;
}
}We want to create a GraduateStudent class that inherits from
Student. We need to add a thesis topic for each graduate student.
Likewise, we need to update the toString() method so that outputs the
appropriate data. We use 4 as the year value for graduate students.
Student to add graduate student capabilities.public class GraduateStudent extends Student {
private String topic; (1)
public GraduateStudent(String name, double GPA, String topic) {
super(name, 4, GPA); (2)
setTopic(topic);
}
public void setTopic(String topic) { this.topic = topic; }
public String toString() { (3)
return getName() + "\tGraduate\t" + getGPA() + "\tTopic: " + topic;
}
}| 1 | Because we’re inheriting most of the fields we need, we only need to
declare the topic field. |
| 2 | Then, in the GraduateStudent constructor,
we call the parent constructor with the name, year, and GPA and then set
topic to the input value. |
| 3 | Finally, we override the toString() method so that "Graduate" and
the thesis topic are output. Note that we must use the getName() and
getGPA() accessors since those fields are private in Student. |
Most code that uses Student objects should be able to incorporate
GraduateStudent objects easily. Code that creates Student objects
from input will need slight modifications to handle the thesis topic.
Also, old code that only expects values of 0, 1, 2, or 3 for
year may need to be modified so that it doesn’t break.
Let’s examine a class hierarchy used to create several different
polygons. Our base class needs to be general. It can represent any kind
of closed polygon, using an array of Point objects. The Point library class
is a way to package up x and y values of type int. Each coordinate
in the array gives the next vertex of the polygon.
import java.awt.*; (1)
public class Polygon {
protected Point[] points; (2)
public Polygon(Point[] points) { (3)
this.points = points;
}| 1 | The import statement allows us to use the Point class as well as the
Graphics class. |
| 2 | Our array of type Point is declared protected so
that the child classes we want to create can access it directly. |
| 3 | The constructor takes an array of type Point and stores it. |
public double getPerimeter() { (1)
double perimeter = 0.0;
for(int i = 0; i < points.length - 1; i++)
perimeter += points[i].distance(points[i + 1]);
perimeter += points[0].distance(points[points.length - 1]);
return perimeter;
}
public void draw(Graphics g) { (2)
for(int i = 0; i < points.length - 1; i++)
g.drawLine(points[i].x, points[i].y, points[i+1].x, points[i+1].y);
g.drawLine(points[0].x, points[0].y,
points[points.length - 1].x, points[points.length - 1].y);
}
}| 1 | The getPerimeter() method can determine the length
of the perimeter by adding the lengths of the segments connecting the
vertices. Although it’s also possible to determine the area enclosed by a list of
vertices, the algorithm is complex. |
| 2 | The draw() method draws the
polygon by drawing each line segment that connects adjacent vertices. We
discuss the Graphics class in Chapter 15. If you compile and run this code, please note that in
Java graphics, like many computer graphics environments, the upper left
hand corner of the screen or window is considered (0,0), and
y values increase going downward, not upward. |
The number of things that can be done with this very general Polygon
class are limited, but with this basic parent class defined, we can
design a Triangle class as a child of it.
import java.awt.*; (1)
public class Triangle extends Polygon {
public Triangle(int x1, int y1, int x2, int y2, int x3, int y3) { (2)
super(toPointArray(x1, y1, x2, y2, x3, y3));
}
protected static Point[] toPointArray(int x1, int y1, int x2, int y2, int x3, int y3) {
Point[] array = {new Point(x1, y1), new Point(x2, y2), new Point(x3, y3)}; (3)
return array;
}| 1 | Again, the import statement is for the Point class. |
| 2 | One reasonable
constructor for a triangle takes in six values, giving the
x and y coordinates of the three vertices of
the triangle. Of course, the Polygon class requires an array of type
Point, but the super constructor must be the first line of the
Triangle constructor. |
| 3 | To solve this problem, we create a static
method to package the values into an array. We could have done the same
thing in the argument list of the super constructor, but it would have
looked messier. The toPointArray() is protected because there’s no
reason to let external code have access to it. |
public String getType() {
double a = points[0].distance(points[1]);
double b = points[1].distance(points[2]);
double c = points[2].distance(points[0]);
if(a == b && b == c)
return "Equilateral";
if(a == b || b == c || a == c)
return "Isosceles";
return "Scalene";
}
}Finally, the getType() method allows us to do something specific with
triangles. We can use the distance() method from the Point class to
find the length of each of the three sides. By comparing these lengths,
we can determine whether the triangle represented is equilateral,
isosceles, or scalene. Of course, computing the perimeter and drawing
the triangle are already taken care of by the Polygon class.
We can easily make a Rectangle class along the same lines.
import java.awt.*;
public class Rectangle extends Polygon {
public Rectangle(int x, int y, int length, int width) { (1)
super(toArray(x, y, length, width));
}
protected static Point[] toArray(int x, int y, int length, int width) { (2)
Point[] array = {new Point(x, y), new Point(x + length, y),
new Point(x + length, y + width), new Point(x, y + width)};
return array;
}
public int getArea() { (3)
int length = points[1].x - points[0].x;
int width = points[2].y - points[1].y;
return length * width;
}
}| 1 | The constructor is similar to the Triangle constructor except that the
upper left corner of the rectangle is specified, along with the length
and the width. |
| 2 | From these values, the appropriate array of Point
values is generated. |
| 3 | The rectangle-specific code that we add is the
getArea() method, which determines the length and width of the
rectangle by examining the points array and then calculates area. |
Using inheritance as form of specialization, we can go one step further
and make a Square class.
public class Square extends Rectangle {
public Square(int x, int y, int size) {
super(x, y, size, size);
}
}This very short class uses everything available in Rectangle but
simplifies the constructor slightly so that the user doesn’t have to
enter both length and width.
11.5. Solution: Boolean circuits
Here we present our solution to the Boolean Circuits problem. First, we
define a parent class for all circuit components, called Gate.
public class Gate {
private String name;
public Gate(String name) { this.name = name; }
public String getName() { return name; }
public String toString() {
return getName() + ": " + getValue();
}
public boolean getValue() { return false; }
}The Gate class doesn’t do anything except set up ways to store a name
and to get a value. It
doesn’t really matter what getValue() gives back for Gate, but we
can say that it’s false.
In principle, it shouldn’t be possible to create an object of type Gate,
UnaryOperator, or BinaryOperator. Classes that are designed only to
be parent classes and never to be instantiated are called abstract classes and
are discussed in Section 17.3.1.
From Gate, we can define the most basic circuit
components: gates whose value is either always true or always false.
public class True extends Gate {
public True() { super("true"); }
public boolean getValue() { return true; }
}public class False extends Gate {
public False() { super("false"); }
public boolean getValue() { return false; }
}To conform with the constructor for Gate, these new classes must pass
a String giving their name to the super constructor. The values
returned by the getValue() method are clear. Next, we want to create a
class that can be used as a parent for all unary operators.
public class UnaryOperator extends Gate {
private Gate input;
public UnaryOperator(String name) { super(name); }
public void setInput(Gate input) { this.input = input; }
public Gate getInput() { return input; }
}The important addition in the UnaryOperator class is the input
field. Any unary operator must have a single input gate that it operates
on. This class provides a mutator and accessor for input, as well as
an appropriate constructor. From UnaryOperator, we can derive two
specific operators.
public class Output extends UnaryOperator {
public Output(int i) { super("OUTPUT " + i); }
public boolean getValue() { return getInput().getValue(); }
}The Output class takes in an int value and uses it to make a
numbered name. Its getValue() method simply returns the value of its
input. The Output class doesn’t do anything except serve as a marker
for circuit output.
public class Not extends UnaryOperator {
public Not() { super("NOT"); }
public boolean getValue() { return !getInput().getValue(); }
}The Not class uses "NOT" as the name supplied to
the super constructor and returns the logical NOT of the value of its
input.
Just as we did for unary operators, we also need a parent class for binary operators.
public class BinaryOperator extends Gate {
private Gate operand1;
private Gate operand2;
public BinaryOperator(String name) { super(name); }
public Gate getOperand1() { return operand1; }
public Gate getOperand2() { return operand2; }
public void setOperand1(Gate operand) { operand1 = operand; }
public void setOperand2(Gate operand) { operand2 = operand; }
}A BinaryOperator has two Gate fields, operand1 and operand2,
representing the inputs to the operator. The BinaryOperator class has
an appropriate constructor and then accessors and mutators for the
operands. With BinaryOperator as a parent, only a few lines of code
are necessary to define any logical binary operator.
public class And extends BinaryOperator {
public And() { super("AND"); }
public boolean getValue() {
return getOperand1().getValue() && getOperand1().getValue();
}
}public class Or extends BinaryOperator {
public Or() { super("OR"); }
public boolean getValue() {
return getOperand1().getValue() || getOperand1().getValue();
}
}public class Xor extends BinaryOperator {
public Xor() { super("XOR"); }
public boolean getValue() {
return getOperand1().getValue() ^ getOperand1().getValue();
}
}In each case, a constructor passes the name of the gate to the super
constructor. Then, each getValue() method gets the values from the two
operands and combines them with AND, OR, or XOR, respectively. This
design allows the programmer to focus only on the important element of
each class. Adding new classes for NAND, NOR, or any other possible
logical binary operator would be quick.
The client code that uses these classes to simulate a circuit follows.
import java.util.*;
public class BooleanCircuit {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int count = in.nextInt();
Gate[] gates = new Gate[count];
String name;
int value;First we have the import needed for Scanner. In main(), we read in the
total number of gates, create an array of type Gate of that length,
and declare a few useful temporary variables.
// Create gates
for(int i = 0; i < count; i++) {
name = in.next().toUpperCase();
if(name.equals("true"))
gates[i] = new True();
else if(name.equals("false"))
gates[i] = new False();
else if(name.equals("AND"))
gates[i] = new And();
else if(name.equals("OR"))
gates[i] = new Or();
else if(name.equals("XOR"))
gates[i] = new Xor();
else if(name.equals("NOT"))
gates[i] = new Not();
else if(name.equals("OUTPUT")) {
value = in.nextInt();
gates[i] = new Output(value);
}
} Then, we parse the input, creating an appropriate gate based on the name read in. In the case of an OUTPUT gate, we must also read in a number so that we can identify which OUTPUT gate is which later.
//connect gates
while(in.hasNextInt()) {
value = in.nextInt();
name = gates[value].getName();
if(name.equals("AND") || name.equals("OR") || name.equals("XOR")) {
BinaryOperator operator = (BinaryOperator)gates[value];
operator.setOperand1(gates[in.nextInt()]);
operator.setOperand2(gates[in.nextInt()]);
}
else if(name.equals("NOT") || name.startsWith("OUTPUT")) {
UnaryOperator operator = (UnaryOperator)gates[value];
operator.setInput(gates[in.nextInt()]);
}
}As long as there’s input remaining, we read in an index. Based on the name of the gate at that index in the array, we either read in two more indexes (for binary operators) or just a single additional index (for unary operators). In either case, we set the input or inputs of the operator to the gate or gates at those indexes.
// Compute output
for(int i = 0; i < count; i++)
if(gates[i].getName().startsWith("OUTPUT"))
System.out.println(gates[i]);
}
}Finally, the simulation of the circuit is surprisingly simple. We look
through array until we find a gate whose name starts with "OUTPUT".
Then, we print out its value. In order to determine its value, it will
ask its input what its value is, which in turn will ask for the values
from its input. The toString() in the Gate class will assure us that
the final output is nicely formatted. This system accommodates any
number of output gates connected arbitrarily, as long as the circuit has
no loops inside of it, such as an AND gate whose output is also one of
its inputs.
11.6. Concurrency: Inheritance
Like interfaces, inheritance in Java is not closely related to concurrency. However, two ways in which inheritance interacts with concurrency deserve attention.
The first is the Thread class. Each thread of execution in Java
(except the main thread) is managed with a Thread object or an object
whose type inherits from Thread. Creating such types is done by
extending Thread, just as you would extend any other class. Further
information about extending Thread for concurrency is given in
Section 13.4. Extending the Thread class to make
your own customized threads of execution is an alternative to
implementing the Runnable interface mentioned in
Section 10.6 and is discussed in greater detail in
Section 13.4.5.
The second interaction between inheritance and concurrency is again very
similar to the problem with interfaces and concurrency: There’s no way
to specify that a method is thread-safe. Recall that it’s not allowed
to use the synchronized keyword on a method in an interface
declaration. Likewise, there’s no restriction on overriding a
synchronized method with a non-synchronized method or vice versa.
The rules for overriding methods in Java guarantee that an object of a child class is usable anywhere that an object of the parent class is usable. Thus, you cannot override a public method with a private one, reducing the visibility of a method. We discuss a similar restriction with exceptions in Section 17.3.4.
If it has these restrictions, why doesn’t Java prevent a synchronized method from being overridden by a non-synchronized method? In the first place, a non-synchronized method can be used anywhere a synchronized one could (unlike a private method, which is not accessible everywhere a public one is). In the second, the designers of Java put thread safety in the category of implementation details left up to the programmer. Some classes need specific methods to be synchronized and others (even child classes) do not. However, if you override a class with a synchronized method, it’s safest to mark your method synchronized as well.
11.7. Exercises
Conceptual Problems
-
Give three advantages of using inheritance instead of copying and pasting code from a parent class. Are there any disadvantages to using inheritance?
-
Consider classes
RadishandCarrotwhich both extend classVegetableand implement interfaceCrunchable. Which of the following sets of assignments are legal and why?-
Radish radish = new Radish(); -
Radish radish = new Vegetable(); -
Vegetable vegetable = new Radish(); -
Crunchable crunchy = new Radish(); -
Radish radish = new Carrot();
-
-
In the context of inheritance, the keyword
supercan be used for two different purposes. What are they? -
Consider the following class definitions.
public class A { private String value; public A(String s) { value = "A" + s + "A"; } public String toString() { return value; } } public class B extends A { public B(String s) { super("B" + s + "B"); } } public class C extends B { public C(String s) { super("C" + s + "C"); } }What’s output by the following code fragment?
C c = new C("ABC"); System.out.println(c); -
Beginning Java programmers often confuse package-private access (no explicit specifier) with
publicaccess. How is this confusion possible when default access is more constrained than bothpublicandprotectedaccess? (Hint: The file system plays a role.) -
What are the similarities and differences between overloading a method and overriding a method?
-
What’s field hiding? How can software bugs arise from this Java feature?
-
Give reasons why the designers of Java decided not to allow multiple inheritance. Would you have made the same decision? Why or why not?
-
Draw a class hierarchy establishing a sensible relationship between the
Human,Soldier,Sailor,Marine,General, andAdmiralclasses. For this class hierarchy, refer to the U.S. military structure in which the U.S. Marine Corps is a part of the U.S. Navy.
Programming Practice
-
Create an
InternationalStudentclass that extendsStudent. It should includeStringfields for country of origin and visa status. It should include mutator and accessor methods for these two new fields. -
Add
PentagonandHexagonclasses that extend thePolygonclass. The constructor for each class should take an x, y and radius value, each ofinttype. Both classes should be implemented to create regular polygons, that is, polygons in which all five or six sides have the same length. The x and y values should give the center of the polygon, and each of the five or six points should be the radius distance away from that center.Because the internal structure of
Polygonkeeps all vertices asPointvalues, the x and y coordinates of the points must beintvalues. This requirement will force you to round these x and y coordinates after using trigonometry to determine their locations. As a result, the final pentagons and hexagons stored and displayed will be slightly irregular. -
The inheritance design of our solution to the Boolean circuits problem given in Section 11.5 makes adding new gates easy. Add classes that implement a NAND gate and a NOR gate. Then, rewrite the
main()method ofBooleanCircuitto accommodate these two extra classes. -
Re-implement the object hierarchy in the solution from Section 10.5 to the sort it out problem. This time, let the
Cat,Dog, andPersonclasses extend theCreatureclass defined below.public class Creature implements Ageable, Weighable { protected int age; protected double weight; public Creature(int age, double weight) { this.age = age; this.weight = weight; } public int getAge() { return age; } public double getWeight() { return weight; } }Refactor your code so that the
Cat,Dog, andPersonclasses are as short as possible. How many lines of code do you save? -
Design a celestial body simulator. You’ll need to create a class containing fields for the x, y, and z locations, x, y, and z velocities, radii, and masses of each object. For each time step of length t, you must do the following.
-
Compute the sum of forces exerted on each body by every other body. The equation for gravitational force on body b exerted by body a is given by the following equation.
As mentioned in Example 8.1, the gravitational constant G = 6.673 × 10-11 N·m2·kg-2. Also, |rab| is the distance between the centers of objects a and b. Finally, the unit vector between the centers of the two objects is given by the equation below.
-
Compute the x, y, and z components of the acceleration vector a for each object using the equation F = ma once the sum of forces has been calculated.
-
Update the x, y, and z components of the velocity vector v for each object using the equation vnew = vold + at.
-
Experiments
-
Inheritance is a powerful technique, but it comes with some overhead costs. Create a class called
Awith the following implementation.public class A { protected int a; }Then, create 25 more classes named
BthroughZ. ClassBshould extendAand add aprotectedintfield calledb. Continue in this manner, with each new class extending the previous one and adding anintfield named the lowercase version of the class name. Thus, if you create an object of typeZ, it will contain, through inheritance, 26intfields namedathroughz. But for a singleZobject to be created, it must call 27 (Zback throughAplusObject) constructors. You may wish to use the file I/O material in Chapter 20 to write a program to create all these classes so that you do not have to do so by hand.Finally, create a new class called
Allwhich contains 26protectedfields ofinttype namedathroughz. Now, the purpose of creating all these classes is to compare the time needed to instantiate an object of typeZwith one of typeAll, though they both only contain 26intfields namedathroughz.Create an array of 100,000 elements of type
Zand then populate it with 100,000Zobjects. Time this process. Create an array of 100,000 elements of typeAlland then populate that array with 100,000Allobjects. You may wish to use theSystem.nanoTime()method described in Chapter 13 to accurately time these processes. Is there a significant difference in the times you found?
12. Exceptions
The vulgar mind always mistakes the exceptional for the important.
12.1. Problem: Bank burglary
Let’s consider a problem in which various aspects of a bank burglary are modeled as Java objects. You want to write some code that will accomplish the following steps:
-
Disable the burglar alarm
-
Break into the bank
-
Find the vault
-
Open the vault
-
Carry away the loot
But any number of things could go wrong! When trying to disable the burglar alarm, you might set it off. When you try to break into the bank, you might have thought that you’d disabled the burglar alarm but actually failed to do so. The door of the bank might be too difficult to open. The vault might be impossible to find, or the vault might be impossible to open. It could even be empty! The money might be made of enormous gold blocks that are too heavy to carry away. Finally, at any time during the heist, a night watchman might catch you in the act.
If you’re the criminal mastermind who planned this deed, you need to know if (and preferably how) your henchman bungled the burglary. You need a simple system that can inform you of any errors that have occurred along the way. Likewise, you need to be able to react differently depending on what went wrong.
We are going to model each of these error conditions with Java
exceptions. An exception is how Java indicates exceptional or
incorrect situations inside of a program. These exceptions are thrown
when the error happens. You must then write code to catch the error
and deal with it appropriately. The bank burglar program will deal with
three different classes, Bank, Vault, and Loot.
The Bank class has three methods, disableAlarm(), breakIn(), and
findVault(), which returns a Vault object. The Vault class has an
open() method and a getLoot() method, which returns a Loot object.
The Loot class has a carryAway() method. Below is a table of the
exceptions which can be thrown by each of the methods.
| Class | Method | Exceptions |
|---|---|---|
Bank |
disableAlarm() |
BurglarAlarmException |
WatchmanException |
||
breakIn() |
BurglarAlarmException |
|
LockPickFailException |
||
WatchmanException |
||
findVault() |
WatchmanException |
|
Vault |
open() |
LockPickFailException |
WatchmanException |
||
getLoot() |
WatchmanException |
|
Loot |
carryAway() |
LootTooHeavyException |
WatchmanException |
In order to deal with each of these possible errors, you need some special Java syntax.
12.2. Concepts: Error handling
As a rule, computer programs are filled with errors. Writing a program is a difficult and complex process. Even if a segment of code is free from errors, it may call other code which contains mistakes. The user could be making mistakes and issuing commands to a program that are impossible to execute. Even hardware can produce errors, as in a hard drive crash or a network connectivity problem.
12.2.1. Error codes
A robust program should deal with as many errors as possible. One
strategy is to have every method give back a special error code
corresponding to an error when it occurs. Then, the code
calling the method can react appropriately. Of course, many methods do
not return a numerical type, limiting this kind of error handling. A
solution that was very common in the C language, particularly in Unix
system calls, was to set a globally visible int variable called
errno to a value corresponding to the error that has just happened.
These approaches have a number of drawbacks. In the case of errno, if a
number of different threads were running at the same time, different
errors could occur simultaneously, but only one value could be kept in
errno. For any system that relies on checking for an error condition
after each method call, a large amount of error handling code must be
mixed in with normal code. Doing so reduces code readability and makes
it difficult to handle errors in a central place. Likewise, a numerical value
doesn’t describe the error, requiring good documentation to know what
the number means.
12.2.2. Exceptions
Java adopts a different error handling strategy called exceptions.
Whenever a specified error state or unusual situation is reached, an
exception is thrown. When an exception is thrown, normal execution stops
immediately. The JVM starts backtracking, looking for code that’s designed to deal with
that specific exception. The code that will handle the exception can be
in the current method, in the calling method, in the caller of the
calling method, or arbitrarily far back in the chain of method calls,
all the way to main(). Each method will return, looking for code to
handle this exception, until it’s found. If no handling code is found,
the exception will propagate all the way past main(), and
the program will end.
Exceptions give a unified and simple way to handle all errors. You can choose to deal with errors directly or delegate that responsibility to methods that call the code you’ve written. Selection statements and loops are forms of local control flow, but exceptions give us the power of non-local control flow, able to jump back through any number of method calls.
12.3. Syntax: Exceptions in Java
In Java syntax, there are two important sides of using exceptions:
throwing the exception when an error occurs and then handling that
exception properly. Below we explain both of these as well as the
catch or specify requirement, the finally keyword, and the process of
creating custom exceptions.
12.3.1. Throwing exceptions
By now you’ve probably experienced a NullPointerException in the
process of coding. This exception happens when an object reference is
null but we try to access one of its methods or fields.
String text = null;
int x = text.length(); // NullPointerExceptionIn this case, the exception is thrown by the JVM itself. It is possible
to catch this exception and deal with it, but a NullPointerException
generally means a mistake in the program, not an error that can be
recovered from. Although many useful exceptions such as NullPointerException,
ArithmeticException, and ArrayIndexOutOfBoundsException are implicitly
thrown by the JVM, we’re also allowed to throw them explicitly.
if(y < 14)
throw new NullPointerException();Like any other object, we use the new keyword to instantiate a
NullPointerException using its default constructor. Once created, we
use the throw keyword to cause the exception to go into effect. Any
exception you throw explicitly must use the throw keyword, but the
majority of exceptions thrown by your programs will either be mistakes
or exceptions thrown by library code you’re calling. If you write a
significant amount of library or API code, you might use throw more
often.
12.3.2. Handling exceptions
Normal application programmers will find themselves writing code that
handles exceptions much more often than code that throws them. In order
to catch an exception, you must enclose the code you think is going
to throw an exception in a try block. Immediately after the try
block, you can list one or more catch blocks. The first catch
block that matches your exception will be executed.
try {
String text = null;
int x = text.length(); // NullPointerException
System.out.println("This will never be printed.");
}
catch(NullPointerException e) {
System.out.println("Surprise! A NullPointerException!");
}In this case, trying to access the length() method of a null
reference will still throw a NullPointerException, but now it’ll be
caught by the catch block below. The message
"Surprise! A NullPointerException!" will be printed to the screen, and
execution will continue normally after the catch block. Once the
exception is caught, it stops trying to propagate. Of course, whatever
the code was doing when the exception was thrown was abandoned
immediately because it might have depended on successful execution of
the code that threw the exception. Thus, the call to the
System.out.println() method in the try block will never be executed.
An exception will match the first catch block with the same class or
any superclass. Since Exception is the parent of RuntimeException
which is the parent of NullPointerException, we could write our
example with Exception instead.
try {
String text = null;
int x = text.length(); // NullPointerException
System.out.println("This will never be printed.");
}
catch(Exception e) {
System.out.println("Well, of course you got a NullPointerException!");
}In general, you should write the most specific exception class possible
for your catch blocks. Otherwise, you might be catching a different
exception than you planned for, preventing that exception from propagating
up to an appropriate handler. For example, the following code will randomly
throw either a NullPointerException or an
ArithmeticException (because of a division by 0).
try {
String text = null;
int x;
if(Math.random() > 0.5)
x = text.length(); // NullPointerException
else
x = 5 / 0; // ArithmeticException
}
catch(Exception e) {
System.out.println("You got some kind of exception!");
}This code will catch either kind of exception, but it won’t tell you
which you got. Instead, the correct approach is to have one catch
block for each possible kind of exception.
try {
String text = null;
int x;
if(Math.random() > 0.5)
x = text.length(); // NullPointerException
else
x = 5 / 0; // ArithmeticException
}
catch(NullPointerException e) {
System.out.println("You used a null pointer!");
}
catch(ArithmeticException e) {
System.out.println("You divided by zero!");
}The list of catch blocks can be arbitrarily long. You must always go
from the most specific exceptions to the most general, like Exception,
otherwise some exceptions could never be reached. The Java compiler
enforces this requirement. The e is a reference to the exception
itself, which behaves something like a parameter in a method. It’s
common to use e as the identifier, but you’re allowed to call it any
legal variable name. Usually, the kind of exception is all you need to
know, but every exception is an object and has fields and methods.
Particularly useful is the getMessage() method which can give
additional information about the exception.
12.3.3. Catch or specify
In contrast to the examples given above, you’ll rarely write code to catch a
NullPointerException or an ArithmeticException. Both of these
exceptions are called unchecked exceptions. In
Chapter 6, we used the Thread.sleep() method to put
the execution of our program to sleep for a short period of time. We
were forced to enclose this method call in a try block with a catch
block for InterruptedException.
try{
Thread.sleep(100);
}
catch(InterruptedException e) {
System.out.println("Wake up!");
}An InterruptedException is thrown when another thread tells your
thread of execution to wake up before it finishes sleeping or waiting.
This exception is a checked exception, meaning that Java insists that
you use a try-catch pair anytime there’s even a chance of it being
thrown. Otherwise, your code won’t compile.
Checked exceptions are those exceptions that your program must plan for. Library and API code often throw checked exceptions. For example, when trying to open a file with an API call, it’s possible that no file with that name exists or that the user might not have permission to access it. A program should catch the corresponding exceptions and recover rather than crashing. Perhaps the program should prompt the user for a new name or explain that the required permission is not set.
In Chapter 6, there were no executable statements in
the catch block used with the Thread.sleep() method. However, you
should never write an empty catch block. Doing so allows errors to fail silently.
We’re allowed to put code that can throw a checked exception into a
try-catch block, but there’s another option. Java has a catch
or specify requirement, meaning that your code is required either to
catch a checked exception or to specify that it has the potential for
causing that exception. To specify that a method can throw certain
exceptions, we use the throws keyword. Note that this is not the
same as the throw keyword.
public static void sleepWithoutTry(int milliseconds) throws InterruptedException {
Thread.sleep(milliseconds);
}In this case, there’s no need for a try-catch block because the
method announces that it has a risk of throwing an
InterruptedException. Of course, any code that uses this method will
have to have a try-catch block or specify that it also throws
InterruptedException. A method can throw many different exceptions,
and you can simply list them out after the throws keyword, separated
by commas.
Almost every exception thrown in Java is a child class of Exception,
RuntimeException, or Error. Any descendant of RuntimeException or
Error is an unchecked exception and is exempt from the catch or
specify requirement. Any direct descendant of Exception is a checked
exception and must either be caught with a try-catch block or
specified with the throws keyword. We say direct descendant because
RuntimeException is a child of Exception, leading to the confusing
situation where only those descendants of Exception which are not also
descendants of RuntimeException are checked.
12.3.4. The finally keyword
To deal with the situation in which an important cleanup or finalizing
task must be done no matter what, the designers of Java introduced the
finally keyword. A finally block comes after all the catch blocks
following a try block. The code inside the finally block will be
executed whether or not any exception was thrown. A finally block is
often used with file I/O to close the file, which should be closed
whether or not something went wrong in the process of reading it, as
we’ll demonstrate in Section 20.3.2.
The finally keyword is unusually powerful. If an exception isn’t
caught and propagates up another level, the finally block will be
executed before propagating the exception. Even a return statement
will wait for a finally block to be executed before returning, leading
to the following bizarre possibility.
public static boolean neverTrue() {
try {
return true;
}
finally {
return false;
}
}This method attempts to return true, but before it can finish, the
finally block returns false. Only one value can be returned, and the
finally block wins. You should be aware of finally blocks and their
unusual semantics. Use them sparingly and only for careful cleanup
operations when needed to guarantee that some event occurs.
Code in a finally block will execute no matter what unless the JVM
exits or the thread in question terminates.
12.3.5. Customized exceptions
Exceptions are most useful when dealing with problems encountered by API code. In those cases, your code must merely catch exceptions defined by someone else; however, it’s sometimes useful to define your own exceptions. For one thing, you might write some API code yourself. Generally, you’ll want to use the standard exceptions whenever possible, but your code might generate some unusual or specific error condition that you want to communicate to a programmer, using your own exception.
Defining a new exception is surprisingly simple. All you have to do is
write a class that extends Exception. Theoretically, you could
extend RuntimeException or Error instead, but you typically won’t.
Children of RuntimeException are intended to indicate a bug in
the program, and children of Error are intended to indicate a system
error.
When creating your new exception, you don’t even have to create
any methods, but it’s wise to implement a default constructor and one
that takes a String as an additional message.
public class EndOfWorldException extends Exception {
public EndOfWorldException() {}
public EndOfWorldException(String message) {
super(message);
}
}As with all other classes, your exceptions should be named in a readable
way. This exception is apparently thrown when the world ends. It’s
considered good style to end the name of any exception class with
Exception. An exception class is a fully fledged class. If you need to
add other fields or methods to give your exception the functionality it
needs, go ahead. However, the main value of an exception lies in
its existence as a named error, not in any tricks it can perform.
Here we’ll give a few examples of exception handling, although
exceptions are more useful in large systems with heavy API use. We’ll
start with an example of a simple calculator that detects division by
zero, then look at exceptions as a tool to detect array bounds problems,
and end with a custom exception used with the Color class.
Here we implement a quick calculator that reads input from the user
in the form of integer operator integer, where operator is one
of the four basic arithmetic operators (+, -, *, /). Our code
will perform the appropriate operation and output the answer, but we’ll
use exception handling to avoid killing the program when a division
by zero occurs.
import java.util.*;
public class QuickCalculator {
public static void main(String[] args){
Scanner in = new Scanner(System.in);
int answer = 0;
String line = in.nextLine().trim().toLowerCase(); (1)
while(!line.equals("quit")) { (2)
String[] terms = line.split(" "); (3)
int a = Integer.parseInt(terms[0]);
char operator = terms[1].charAt(0);
int b = Integer.parseInt(terms[2]);| 1 | The program reads a line of input from the user. |
| 2 | It tests to see if it’s the sentinel value "quit". |
| 3 | If it isn’t, the program parses it into two int values and a char. |
try{ (1)
switch(operator) { (2)
case '+': answer = a + b; break;
case '-': answer = a - b; break;
case '*': answer = a * b; break;
case '/': answer = a / b; break;
}
System.out.println("Answer: " + answer); (3)
}
catch(ArithmeticException e) { (4)
System.out.println("You can't divide by 0!");
}
line = in.nextLine().trim().toLowerCase();
}
}
}| 1 | Here we have a try block enclosing the code where the operations
occur. |
| 2 | Inside the switch statement, the code blindly performs
addition, subtraction, multiplication, or division, depending on the
value of operator. |
| 3 | Then, it prints the answer. |
| 4 | However, if a division by zero occurs, the execution jumps to the catch block
and prints an appropriate message. |
This try-catch pair is situated
inside the loop so that the input will continue even if there was a
division by zero. We could achieve the same effect by using an if
statement to test if the divisor is zero, but our solution allows easy
extensions if there are other exceptions we want to catch.
Exceptions provide a lot of power. If we want, we can use the
ArrayOutOfBoundsException as a crutch when we don’t want to think
about the bounds of our array. Although this makes for an interesting
example, exceptions should not be used in Java to perform normal tasks.
This method takes in an array of int values and prints them all out.
public static void exceptionalArrayPrint(int[] array) {
try {
int i = 0;
while(true)
System.out.print(array[i++] + " ");
}
catch(ArrayIndexOutOfBoundsException e) {}
}Although the while loop will run without stopping, the moment that i
reaches array.length, it will throw an ArrayIndexOutOfBoundsException when
it tries to access that element in array. Since we left the catch
block empty, nothing will happen, the method will return, and everything
will work fine. This example is a peculiar kind of laziness, indeed,
since a for loop could achieve the same effect with fewer lines of
code.
Programmers can be tempted to abuse exceptions in this way when a lot of calculations are needed to determine the correct bounds. Consider a game of Connect Four. To see if a player has won, the computer must examine all horizontal, vertical, and diagonal possibilities for four in a row. If the game board is represented as a 2D array, the programmer must be careful to make sure that checking for four in a row does not access any index greater than the last row or column or smaller than 0.
The danger of using exceptions for these kinds of tasks has several sources. First, the programmer may not deeply understand the problem and may be careless about the solution. Second, there’s a risk of hiding exceptions that are generated because of real errors. Third, the code becomes difficult to read and unintuitive. Finally, excessive use of exceptions can negatively impact performance.
The Color class provided by Java allows us to represent a color as a
triple of red, green, and blue values with each value in the range
[0,255]. Using these three components, we can produce
2563 = 16,777,216 colors. If we were programming some
image manipulation software, we might want to be able to increase the
red, green, or blue values separately. If changing a value makes it
larger than 255, we could throw an exception. Likewise, if changing a
value makes it less than 0, we could throw a different exception. Let’s
give two custom exceptions that could serve in these roles.
public class ColorUnderflowException extends Exception {
public ColorUnderflowException(String message) {
super(message);
}
public ColorUnderflowException() { super(); }
}public class ColorOverflowException extends Exception {
public ColorOverflowException(String message) {
super(message);
}
public ColorOverflowException() { super(); }
}Now we can write six methods, each of which increases or decreases the
red, green, or blue component of a Color object by 5. If the value of
the component is out of range, an appropriate exception will be thrown.
public static Color increaseRed(Color color)
throws ColorOverflowException {
if(color.getRed() + 5 > 255)
throw new ColorOverflowException("Red: " + (color.getRed() + 5));
else
return new Color(color.getRed() + 5, color.getGreen(), color.getBlue());
}
public static Color increaseGreen(Color color)
throws ColorOverflowException {
if(color.getGreen() + 5 > 255)
throw new ColorOverflowException("Green: " + (color.getGreen() + 5));
else
return new Color(color.getRed(), color.getGreen() + 5, color.getBlue());
}
public static Color increaseBlue(Color color)
throws ColorOverflowException {
if(color.getBlue() + 5 > 255)
throw new ColorOverflowException("Blue: " + (color.getBlue() + 5));
else
return new Color(color.getRed(), color.getGreen(), color.getBlue() + 5);
}
public static Color decreaseRed(Color color) throws ColorUnderflowException {
if(color.getRed() - 5 < 0)
throw new ColorUnderflowException("Red: " + (color.getRed() - 5));
else
return new Color(color.getRed() - 5, color.getGreen(), color.getBlue());
}
public static Color decreaseGreen(Color color)
throws ColorUnderflowException {
if(color.getGreen() - 5 < 0)
throw new ColorUnderflowException("Green: " + (color.getGreen() - 5));
else
return new Color(color.getRed(), color.getGreen() - 5, color.getBlue());
}
public static Color decreaseBlue(Color color)
throws ColorUnderflowException {
if(color.getBlue() - 5 < 0)
throw new ColorUnderflowException("Blue: " + (color.getBlue() - 5));
else
return new Color(color.getRed(), color.getGreen(), color.getBlue() - 5);
}Finally, we can write a short method that changes a given color based on user input and deals with exceptions appropriately.
public static Color changeColor(Color color) {
System.out.println("Enter 'R', 'G', or 'B' to increase " +
"the amount of red, green, or blue in your color. " +
"Enter 'r', 'g', or 'b' to decrease the amount of " +
"red, green, or blue in your color.");
Scanner in = new Scanner(System.in);
try {
switch(in.next().trim().charAt(0)) {
case 'R': color = increaseRed(color); break;
case 'G': color = increaseGreen(color); break;
case 'B': color = increaseBlue(color); break;
case 'r': color = decreaseRed(color); break;
case 'g': color = decreaseGreen(color); break;
case 'b': color = decreaseBlue(color); break;
}
}
catch(ColorOverflowException e) {
System.out.println(e);
}
catch(ColorUnderflowException e) {
System.out.println(e);
}
return color;
}The code that uses these methods and exceptions is compact. One try
block enclosing the method calls is needed so that the exceptions can be
caught. Following the try, there’s a catch block for the
ColorOverflowException and one for the ColorUnderflowException. Each
will print out its exception, including the customized message inside.
If an exception occurred, the value of color would remain unchanged
because the execution would have jumped to a catch block before the
assignment could happen.
Note that when catching the ColorOverflowException or the ColorUnderflowException
in the above code, we do the same thing in either case: print the exception.
To reduce the amount of code, we could have caught Exception
instead of those two specific exceptions, but doing so would catch all
exceptions, not just the two related to color that we care about.
In Java 7 and higher, there’s special syntax to deal with situations like the
one above where several specific exceptions are handled in the same way. The
exception types are listed in a catch block with pipe symbols (|) between
them. There’s still only a single reference to the exception (often named
e). Using this updated syntax, we could have written the try-catch above
as follows.
try {
switch(in.next().trim().charAt(0)) {
case 'R': color = increaseRed(color); break;
case 'G': color = increaseGreen(color); break;
case 'B': color = increaseBlue(color); break;
case 'r': color = decreaseRed(color); break;
case 'g': color = decreaseGreen(color); break;
case 'b': color = decreaseBlue(color); break;
}
}
catch(ColorOverflowException | ColorUnderflowException e) {
System.out.println(e);
}12.4. Solution: Bank burglary
Here’s our solution to the bank burglary problem. Although somewhat fanciful, the process could be expanded into a more serious simulation. We begin by defining each of the exceptions.
public class BurglarAlarmException extends Exception {
public BurglarAlarmException(String message) {
super(message);
}
public BurglarAlarmException() { super(); }
}public class WatchmanException extends Exception {
public WatchmanException(String message) {
super(message);
}
public WatchmanException() { super(); }
}public class LockPickFailException extends Exception {
public LockPickFailException(String message) {
super(message);
}
public LockPickFailException() { super(); }
}public class LootTooHeavyException extends Exception {
public LootTooHeavyException(String message) {
super(message);
}
public LootTooHeavyException() { super(); }
}Note that the default constructor for each exception is necessary, since
constructors taking a String value are provided for each class.
Although these default constructors do nothing other than call their
parent constructor, they are needed so that it is possible to create
each of these constructors without a customized message.
With the exceptions defined, we can assume that the Bank class and the
Vault class throw the appropriate exceptions when something goes
wrong. Thus, we can make a Henchman class who can try to do the heist
and react appropriately if there’s a problem.
public class Henchman {
public void burgle(Bank bank) { (1)
try {
bank.disableAlarm(); (2)
bank.breakIn();
Vault vault = bank.findVault();
vault.open();
Loot loot = vault.getLoot();
loot.carryAway();
System.out.println("We got " + loot + "!"); (3)
}| 1 | To burgle a bank, one must create a Henchman object then pass a Bank
object into its burgle() method. |
| 2 | The method will try to disable the alarm, break into the bank, find the vault, open the vault, get the loot out of the vault, and carry it away. |
| 3 | If all those steps happen
successfully, the method will print out a String version of the loot. |
All of this code is inside of a try block. If an exception is thrown
at any point, the following catch blocks will deal with it.
catch(BurglarAlarmException e) { (1)
System.out.println("I set off the burglar because " + e.getMessage());
System.out.println("I had to run away.");
}
catch(WatchmanException e) { (2)
System.out.println("A watchman caught me because " + e.getMessage());
System.out.println("Please bail me out of jail.");
}
catch(LockPickFailException e) { (3)
System.out.println("I couldn't pick the vault lock.");
System.out.println("No loot for us.");
}
catch(LootTooHeavyException e) { (4)
System.out.println("The loot was too heavy to carry.");
System.out.println("No loot for us.");
}
catch(NullPointerException e) { (5)
System.out.println("The vault was hidden or empty.");
System.out.println("No loot for us.");
}
}
}| 1 | If a BurglarAlarmException happens, the henchman is forced to run
away. |
| 2 | If a WatchmanException happens, the henchman is caught and must
be bailed out of jail. |
| 3 | If a LockPickFailException the henchman is unable to carry the
loot off. |
| 4 | Something similar happens for a LootTooHeavyException. |
| 5 | The last catch block is a little unusual. In this case, a
NullPointerException has occurred. Within the try block, two obvious
sources of this exception are the vault and the loot variables. If
either of them were null, in the case of a vault that could not be
found or a vault that was empty, trying to call a method on that null
reference would throw a NullPointerException. Although this code shows
the power of exception handling, it’s a little unwieldy since we don’t
know which variable was null. Also, it’ll hide any
NullPointerException that might happen for other reasons. A better
solution would be to check for each of these null cases or create more
specific exceptions thrown by findVault() and getLoot() if either
returns null. |
12.5. Concurrency: Exceptions
Any thread in Java can throw an exception. That thread might be the main thread or it might be an extra one that you spawned yourself. (Or even one spawned behind the scenes through a library call.)
What happens when a thread throws an exception? As we’ve been
discussing in this chapter, the exception will either be caught or
propagate back to its caller. If the exception is caught, the catch block
determines what happens. If the exception propagates back and back and back and
is never caught, then what? If you’ve coded some of the examples in this
chapter, you might think the entire program crashes, but only the thread
throwing the exception dies.
In a program with a single thread, an exception thrown by the main()
method will crash the program, completely halting execution. In a
multi-threaded program, execution will continue on all threads that have
not thrown exceptions. If even a single thread is executing, the program
will run to completion before the JVM shuts down.
public class CrazyThread extends Thread {
private int value;
public static void main(String[] args) {
for(int i = 0; i < 10; i++)
new CrazyThread(i).start();
throw new RuntimeException();
}
public CrazyThread(int value) {
this.value = value;
}
public void run() {
if(value == 7) {
double sum = 0;
for(int i = 1; i <= 1000000; i++)
sum += Math.sin(i);
System.out.println("Sum: " + sum);
}
else
throw new RuntimeException();
}
}In the program given above, all of the threads except one will die
because of the RuntimeException that they throw. Note that we use the unchecked
RuntimeException so that Java does not complain about the lack of
catch blocks. The thread with a value of 7 will complete its
calculation and print it to the screen even though the main thread has
died. For more information on how to spawn threads, refer to
Chapter 13.
This behavior can cause a program that never seems to finish. You might
write a program that spawns a number of threads and does some work. Even
if the main() method has completed and all the important data has been
output, the program won’t terminate if any threads are still alive.
This problem can also be caused by creating a GUI (such as a JFrame),
which spawns one or more threads indirectly, if the GUI isn’t properly
disposed.
12.5.1. InterruptedException
In conjunction with concurrency, one exception deserves special
attention: InterruptedException. This exception can happen when a thread calls
wait(), join(), or sleep(). It’s a checked exception, requiring
either a catch block or a throws specification.
This exception is used in cases where the executing thread must wait for
some event to occur or some time to pass. In extreme circumstances,
another thread can interrupt the waiting thread, forcing it to continue
executing before it’s done waiting. If that happens, the code in the
catch block determines how the thread should recover from being awoken
prematurely.
Programmers who are new to concurrency in Java are often confused or
annoyed by InterruptedException, particularly since it never seems to be thrown.
Although it’s thrown rarely, situations such as a system shutting down
may be best dealt with by calling interrupt() on a waiting thread,
causing such an exception. Although we’ll generally leave the
InterruptedException catch block empty in this book, threads written
for production code should always handle interruptions gracefully.
12.6. Exercises
Conceptual Problems
-
What are the advantages of using exceptions instead of returning error codes?
-
The keywords
finalandfinally, as well as theObjectmethodfinalize(), are sometimes confused. What’s the purpose of each one? -
What’s the difference between the
throwkeyword and thethrowskeyword? -
What must be done differently when using methods that throw checked exceptions as compared to unchecked exceptions? How do the classes
Exception,RuntimeException, andErrorplay a role? -
For every program you write, you could choose to put the entire body of your
main()method in a largetryblock with acatchblock at the end that catchesException. In this way, no exception would cause your program to crash. Why is this approach a bad programming decision? -
Why did the designers of Java choose to make
NullPointerExceptionandArithmeticExceptionunchecked exceptions even though a program that unintentionally dereferences anullpointer or divides by zero will often crash? -
Consider the following two classes.
public class Trouble { public makeTrouble() { throw new ArithmeticException(); } } public class Hazard { public makeHazard() { throw new InterruptedException(); } }Class
Troublewill compile, but classHazardwill not. Explain why and what could be done to makeHazardcompile. -
What value will the following method always return and why?
public static int magic(String value) { try { int x = Integer.parseInt(value); return x; } catch(Exception e) { System.out.println("Some exception occurred."); return 0; } finally { return -1; } } -
Why will the following segment of code fail to compile?
try{ Thread.sleep(1000); } catch(Exception e) { System.out.println("Exception occurred!"); } catch(InterruptedException e) { System.out.println("Woke up early!"); } -
Consider the following fragment of Java.
try { throw new NullPointerException(); } finally { throw new ArrayIndexOutOfBoundsException(); }This code is legal Java. It’s possible to have a
finallyblock after atryblock without anycatchblocks between them. However, only a single exception can be active at once. Which exception will propagate up from this code and why?
Programming Practice
-
The
NumberFormatExceptionexception is thrown whenever theInteger.parseInt()method receives a poorly formattedStringrepresentation of an integer. Re-implementQuickCalculatorto catch anyNumberFormatExceptionand give an appropriate message to the user. -
Refer to Exercise 11.14 and add to the basic mechanics of the simulation by designing two custom exceptions,
CollisionExceptionandLightSpeedException. These exceptions should be thrown, respectively, if two bodies collide or if the total magnitude of a body’s velocity exceeds the speed of light. -
Users often log onto systems by entering their user name and a password. Unfortunately, human beings are notoriously bad at picking passwords. In computer security, a tool called a proactive password checker allows a user to pick a password but rejects the choice if it doesn’t meet certain criteria.
Common criteria for a password are that it must be at least a certain length, must contain must contain uppercase and lowercase letters, must contain numerical digits, must contain symbols, cannot be the same as a list of words from a dictionary, and others.
Write a short program with a
check()method that takes a singleStringparameter giving a possible password. This method should throw an exception if the password does not meet the matching criteria listed below.Password criteria Exception At least 8 characters in length
TooShortException
Contains both upper- and lowercase letters
NoMixedCaseException
Contains at least one numerical digit
NoDigitException
Contains at least one symbol
NoSymbolException
Your
main()method should prompt the user to select a password and then pass it to thecheck()method. If the method throws an exception, you should catch it and print an appropriate error message. Otherwise, you should report to the user that the password is acceptable. Note that you’ll need to define each of the four exceptions as well.
Experiments
-
Throwing and catching exceptions is a useful tool for making robust programs in Java. However, the JVM machinery needed to implement such a powerful tool is complex. Create an array containing 100,000 random
intvalues. First, sum all these variables up using aforloop and time how long it takes. Then, do the same thing, but, inside of theforloop, put atryblock containing a simple division by zero instruction such asx = 5 / 0;. After thetryblock, put acatchblock catching anArithmeticException. Time this version of the code. Again, you may wish to useSystem.nanoTime()to measure the time accurately. Was there a large difference in the time taken? Do your findings have any implications for code that routinely throws thousands of exceptions?
13. Concurrent Programming
Time is the substance from which I am made. Time is a river which carries me along, but I am the river; it is a tiger that devours me, but I am the tiger; it is a fire that consumes me, but I am the fire.
13.1. Introduction
So far we’ve focused mostly on writing sequential programs. Sequential execution means that program statements are executed one at a time in a sequence determined by program logic and input data. However, more than one program statement can be executed independently by a multicore processor. While it’s common for programmers to write sequential programs, the widespread availability of multicore processors in a single computer has led to an increase in the demand for programmers who can write concurrent programs.
A concurrent program is one in which several statements can be executed simultaneously by two or more cores. In this chapter we show how to write simple concurrent programs in Java that exploit the power of a multicore computer. We begin with a problem where the fate of the planet’s in grave danger!
13.2. Problem: Deadly virus
A deadly virus capable of wiping out the world’s population is about to be released by an evil mastermind. Only he knows the security code that can stop the countdown. The world is doomed. The single hope for salvation lies with you and your Java programming skills. Through the investigations of a top secret, government-funded spy ring, it’s been revealed that the security code is tied to the number 59,984,005,171,248,659. This large number is the product of two prime numbers, and the security code is their sum. All you need to do is factor the number 59,984,005,171,248,659 into its two prime factors and add them.
Of course, there’s a catch. The deadly virus is going to be released soon, so soon that there might not be enough time for your computer to search through all the numbers one by one. Instead, you must use concurrency to check more than one number at a time.
Does this problem sound contrived? To keep information sent over the Internet private, many kinds of public key cryptography rely on the difficulty of factoring large numbers. Although factoring the number in this problem isn’t difficult, the numbers used for public key cryptography, typically more than 300 decimal digits long, have resisted factorization by even the fastest computers.
13.3. Concepts: Splitting up work
The deadly virus problem has one large task (factoring a number) to perform. How should we split up this task so that we can do it more quickly? Splitting up the work to be done is at the heart of any concurrent solution to a problem.
In a multicore processor, each core is an independent worker. It takes some care to coordinate these workers. First of all, we still need to get the right answer. A concurrent solution is worthless if it’s incorrect, and by reading and writing to the same shared memory, answers found by one core can corrupt answers found by other cores. Preventing that problem will be addressed in Chapter 14. Once we can guarantee the concurrent solution is correct, we also want to improve performance. Perhaps we want the task to finish more quickly. Perhaps we have an interactive system that should continue to handle user requests even though it’s working on a solution in the background. Again, if the overhead of coordinating our workers takes more time than a sequential solution or makes the system less responsive, it’s not useful.
There are two main ways to split up work. The first is called task decomposition. In this approach, each worker is given a different job to do. The second is called domain decomposition. In this approach, the workers do the same job but to different data.
It’s possible to use both task and domain decomposition together to solve the same problem. With both kinds of decomposition, it’s usually necessary to coordinate the workers so that they can share information. In the next two subsections, we describe task decomposition and domain decomposition in greater depth. Then we discuss mapping tasks to threads of execution and the different memory architectures that can be used for concurrent programming.
13.3.1. Task decomposition
The idea of breaking a task down into smaller subtasks is a natural one. Imagine you’re planning a dinner party. You need to buy supplies, cook the dinner, clean your house, and set the table. If four of you were planning the party, each could perform a separate activity. The preparations could go much faster than if a single person was doing the work, but coordination is still important. Perhaps the person cooking the dinner couldn’t finish until certain supplies were bought.
Task decomposition is often easier than domain decomposition because many tasks have natural divisions. Unfortunately, it’s not always an effective way to use multiple cores on a computer. If one task finishes long before the others, a core might sit idle.
The next two examples give simple illustrations of the process of splitting a task into smaller subtasks in the context of multicore programming.
Consider a simple video game that consists of the following tasks.
-
Start game
-
Process move
-
Update score
-
Repaint screen
-
End game

Suppose that tasks B and D are independent and can be executed concurrently if two cores are available. Task D continually updates the screen with the old data until task C updates the information.
Figure 13.1(a) and (b) show how the tasks in this video game can be sequenced, respectively, on a single core or on two cores. All tasks are executed sequentially on a single-core processor. In a dual-core processor tasks B and C can execute on one core while task D is executing concurrently on another. Note from the figure that task C sends the score and any other data to task D which is continuously updating the screen. Having two cores can allow a faster refresh of the display since the processor doesn’t have to wait for tasks B or C to complete.
Suppose we need to evaluate the mathematical expression 2Kate-at² with parameters a and K at a given value of t. We can divide the expression into two terms: 2Kat and e-at². Each of these terms can be assigned to a different task for evaluation. On a dual-core processor, these two tasks can be executed on separate cores and the results from each combined to find the value of the expression for the main task.

Figure 13.2 shows how this expression can be evaluated on single core and dual-core processors. Sometimes, using multiple cores to evaluate an expression like this will take less time than a single core. However, there’s no guarantee that using multiple cores will always be faster since tasks take time to set up and to communicate with each other.
These examples illustrate how a task can be divided into two or more subtasks executed by different cores of a processor. We use a dual-core processor for our examples, but the same ideas can be expanded to a larger number of cores.
13.3.2. Domain decomposition
In a computer program, every task performs operations on data. This data is called the domain of that task. In domain decomposition, the data is divided into smaller chunks where each chunk is assigned to a different core, instead of dividing a task into subtasks. Thus, each core executes the same task but on different data.
In the example of the dinner party, we could have used domain decomposition instead of (or in addition to) task decomposition. If you want to cook a massive batch of mashed potatoes, you could peel 24 potatoes yourself. However, if there are four people (and each has a potato peeler), each person would only need to peel 6 potatoes.
The strategy of domain decomposition is very useful and is one of the major focuses of concurrency in this book. Problems in modern computing often use massive data, comprising millions of values or thousands of database records. Writing programs that can chop up data so that multiple cores can process smaller sections of it can greatly speed up the time it takes to finish computation.
In some ways, domain decomposition can be more difficult than task decomposition. The data must be divided evenly and fairly. Once each section of data has been processed, the results must be combined. Companies like Google that process massive amounts of information have developed terminology to describe this process. Dividing up the data and assigning it to workers is called the map step. Combining the partial answers into the final answer is called the reduce step.
We illustrate the domain decomposition strategy in the next two examples.
Suppose we want to apply function f to each element of an array a and sum the results. Mathematically, we want to compute the following sum.

In this formula, ai is the ith element of array a. Let’s assume we have a dual-core processor available to compute the sum. We split up the array so that each core performs the task on half of the array. Let S1 and S2 denote the sums computed by core 1 and core 2, respectively.

Assuming that N is even, both cores process exactly the same amount of data. For odd N, one of the cores processes one more data item than the other.

After S1 and S2 have been computed, one of the cores can add these two numbers together to get S. This strategy is illustrated in Figure 13.3. After the two cores have completed their work on each half of the array, the individual sums are added together to produce the final sum.
The need to multiply matrices arises in many mathematical, scientific, and engineering applications. Suppose we’re asked to write a program to multiply two square matrices A and B, which are both n × n matrices. The product matrix C will also be n × n. A sequential program will compute each element of matrix C one at a time. However, a concurrent program can compute more than one element of C simultaneously using multiple cores.

In this problem, the task is to multiply matrices A and B. Through domain decomposition, we can replicate this task on each core. As shown in Figure 13.4, each core computes only a portion of C. For example, if A and B are 4 × 4 matrices, we can ask one core to compute the product of the first two rows of A with all four columns of B to generate the first two rows of C. The second core computes the remaining two rows of C. Both cores can access matrices A and B.
13.3.3. Tasks and threads
It’s the programmer’s responsibility to divide his or her solution into a number of tasks and subtasks which will run on one or more cores on a processor. In previous sections, we described concurrent programs as if specific tasks could be assigned specific cores, but Java doesn’t provide a direct way to do so.
Instead, a Java programmer must group together a set of tasks and subtasks into a thread. A thread is very much like a sequential program. In fact, all sequential programs are made up of a single thread. A thread is a segment of executing code that runs through its instructions step by step. Each thread can run independently. If you have a single core processor, only one thread can run at a time, and all the threads will take turns. If you have a multicore processor, as many threads as there are cores can execute at the same time. You can’t pick which core a given thread will run on. In most cases, you won’t even be able to tell which core a given thread is using.
It takes care to package up the right set of tasks into a single thread of execution. Recall the previous examples of concurrent programming in this chapter.
Consider dividing the tasks in Example 13.1 into two threads. Tasks B and C in can be packaged into thread 1, and task D can be packaged into thread 2. This division is shown in Figure 13.5(a).
Tasks to evaluate different subexpressions in Example 13.2 can also be divided into two threads as shown in Figure 13.5(b). In many problems there are several reasonable ways of dividing a set of subtasks into threads.

Note that these figures look exactly like the earlier figures, except that the tasks are grouped as threads instead of cores. This grouping matches reality better, since we can control how the tasks are packaged into threads but not how they are assigned to cores.
In both examples, we have two threads. It’s possible that some other
thread started these threads running. Every Java program, concurrent or
sequential, starts with one thread. We’ll refer to this thread as the
main thread since it contains the main() method.
Example 13.3 and Example 13.4 use multiple identical tasks, but these tasks operate on different data. In Example 13.3, the two tasks can be assigned to two threads that operate on different portions of the input array. The task of summing the results from the two threads can either be a separate thread or a subtask included in one of the other threads. In Example 13.4, the two tasks can again be assigned to two distinct threads that operate on different parts of the input matrix A to generate the corresponding portions of the output matrix C.
There can be many ways to package tasks into threads. There can also be many ways to decompose data into smaller chunks. The best ways to perform these subdivisions of tasks or data depend on the problem at hand and the processor architecture on which the program will be executed.
13.3.4. Memory architectures and concurrency
The two most important paradigms for concurrent programming are message passing and shared memory systems. Each paradigm handles communication between the various units of code running in parallel in a different way. Message passing systems such as MPI approach this problem by sending messages between otherwise independent units of code called processes. A process which is executing a task may have to wait until it receives a message from another process before it knows how to proceed. Messages can be sent from a single process to one other or broadcast to many. Message passing systems are especially useful when the processors doing the work do not share memory.
In contrast, the built-in system for concurrency in Java uses the shared memory paradigm. In Java, a programmer can create a number of threads which share the same memory space. Each thread is an object which can perform work. We described threads as a way to package up a group of tasks, and processes are another. People use the term processes to describe units of code executing with separate memory and threads to describe units of code executing with shared memory.
When you first learned to program, one of the biggest challenges was probably learning to solve a problem step by step. Each line of the program had to be executed one at a time, logically and deterministically. Human beings don’t naturally think that way. We tend to jump from one thing to another, making inferences and guesses, thinking about two unrelated things at once, and so on. As you know now, it’s only possible to write and debug programs because of the methodical way they work.
You can imagine the execution of a program as an arrow that points to
one line of code, then the next, then the next, and so on. We can think
of the movement of this arrow as the thread of execution of the program.
The code does the actual work, but the arrow keeps track of where
execution in the program currently is. The code can move the arrow
forward, it can do basic arithmetic, it can decide between choices with
if statements, it can do things repeatedly with loops, it can jump
into a method and then come back. A single thread of execution can do
all of these things, but its arrow can’t be two places at once. It can’t
be dividing two numbers in one part of the program and evaluating an
if statement in another. However, there’s a way to split this thread
of execution so that two or more threads are executing different parts
of the program, and the next section will show you how this is done in
Java.
13.4. Syntax: Threads in Java
13.4.1. The Thread class
Java, like many programming languages, includes the necessary features
to package tasks and subtasks into threads. The Thread class and its
subclasses provide the tools for creating and managing threads. For
example, the following class definition allows objects of type
ThreadedTask to be created. Such an object can be executed as a
separate thread.
public class ThreadedTask extends Thread {
// Add constructor and body of class
}The constructor is written just like any other constructor, but there’s
a special run() method in Thread that can be overridden by any of
its subclasses. This method is the starting point for the thread of
execution associated with an instance of the class. Most Java
applications begin with a single main thread which starts in a main()
method. Additional threads must start somewhere, and that place is the
run() method. A Java application will continue to run as long as at
least one thread is active. The following example shows two threads,
each evaluating a separate subexpression as in Figure 13.5(b).
We’ll create Thread1 and Thread2 classes. The threads of execution
created by instances of these classes compute, respectively, the two
subexpressions in Figure 13.5(b) and save the
computed values.
public class Thread1 extends Thread {
private double K, a, t, value;
public Thread1(double K, double a, double t) {
this.K = K;
this.a = a;
this.t = t;
}
public void run() { value = 2*K*a*t; }
public double getValue() { return value; }
}public class Thread2 extends Thread {
private double a, t, value;
public Thread2(double a, double t) {
this.a = a;
this.t = t;
}
public void run() { value = Math.exp(-a*t*t); }
public double getValue() { return value; }
}The run() method in each thread above computes a subexpression and
saves its value. We show how these threads can be executed to solve the
math expression problem in Example 13.6.
13.4.2. Creating a thread object
Creating an object from a subclass of Thread is the same as creating
any other object in Java. For example, we can instantiate the Thread1
class above to create an object called thread1.
Thread1 thread1 = new Thread1(15.1, 2.8, 7.53);Using the new keyword to invoke the constructor creates a Thread1
object, but it doesn’t start executing it as a new thread. As with all
other classes, the constructor initializes the values inside of the new
object. A subclass of Thread can have many different constructors with
whatever parameters its designer thinks appropriate.
13.4.3. Starting a thread
To start the thread object executing, its start() method must be
called. For example, the thread1 object created above can be started
as follows.
thread1.start();Once started, a thread executes independently. Calling the start()
method automatically calls the object’s run() method behind the
scenes. When a thread needs to share data with another thread, it
might have to wait.
13.4.4. Waiting for a thread
Often some thread, main or otherwise, needs to wait for another thread
before proceeding further with its execution. The join() method is
used to wait for a thread to finish executing. For example, whichever
thread executes the following code will wait for thread1 to complete.
thread1.join();Calling join() is a blocking call, meaning that the code calling
this method will wait until it returns. Since it can throw a a checked
InterruptedException while the code’s waiting, the join() method
is generally used within a try-catch block. We can add a
try-catch block to the thread1 example so that we can recover from
being interrupted while waiting for thread1 to finish.
try {
System.out.println("Waiting for thread 1...");
thread1.join();
System.out.println("Thread 1 finished!");
}
catch (InterruptedException e) {
System.out.println("Thread 1 didn't finish!");
}Note that the InterruptedException is thrown because the main thread
was interrupted while waiting for thread1 to finish. If the join()
call returns, then thread1 must have finished, and we inform the user.
If an InterruptedException is thrown, some outside thread must have
interrupted the main thread, forcing it to stop waiting for thread1.
In earlier versions of Java, there was a stop() method which would
stop an executing thread. Although this method still exists, it’s been
deprecated and shouldn’t be used because it can make a program behave
in an unexpected way.
Now that we have the syntax to start threads and wait for them to
finish, we can use the threads defined in Example 13.5 with a
main thread to make our first complete concurrent
program. The main thread in class MathExpression creates and starts
the worker threads thread1 and thread2 and waits for their
completion. When the two threads complete their execution, we can ask
each for its computed value. The main thread then prints the product of
these values, which is the result of the expression we want to evaluate.
public class MathExpression {
public static void main (String[] args) {
double K = 120, a = 1.2, t = 2;
Thread1 thread1 = new Thread1(K, a, t);
Thread2 thread2 = new Thread2(a, t);
thread1.start(); // Start thread1
thread2.start(); // Start thread2
try { // Wait for both threads to complete
thread1.join();
thread2.join();
System.out.println("Value of expression: " +
thread1.getValue()*thread2.getValue());
}
catch (InterruptedException e) {
System.out.println("A thread didn't finish!");
}
}
}We want to make it absolutely clear when threads are created, start executing, and finish. These details are crucial for the finer points of concurrent Java programming. In Figure 13.5, it appears as if execution of the concurrent math expression evaluation begins with Thread 1 which spawns Thread 2. Although that figure explains the basics of task decomposition well, the details are messier for real Java code.
In the code above, execution starts with the main() method in
MathExpression. It creates Thread1 and Thread2 objects and waits
for them to finish. Then, it reads the values from the objects after
they’ve stopped executing. We could have put the main() method in
the Thread1 class, omitting the MathExpression class entirely. Doing
so would make the execution match Figure 13.5
more closely, but it would make the two Thread subclasses less
symmetrical: The main thread and thread1 would both independently
execute code inside the Thread1 class while only thread2 would
execute code inside the Thread2 class.

MathExpression, Thread1, and Thread2.Figure 13.6 shows the execution of thread1 and
thread2 and the main thread. Note that the JVM implicitly creates and starts
the main thread which explicitly creates and starts thread1 and thread2.
Even after the threads associated with thread1 and thread2 have stopped running,
the objects associated with them continue to exist. Their methods and fields can still be
accessed.
13.4.5. The Runnable interface
Although it’s possible to create Java threads by inheriting from the
Thread class directly, the Java API allows the programmer to use an
interface instead.
As an example, the Summer class takes an array of int values and
sums them up within a given range. If multiple instances of this class
are executed as separate threads, each one can sum up different parts of
an array.
public class Summer implements Runnable {
int[] array;
int lower;
int upper;
int sum = 0;
public Summer(int[] array, int lower, int upper) {
this.array = array;
this.lower = lower;
this.upper = upper;
}
public void run() {
for(int i = lower; i < upper; i++)
sum += array[i];
}
public int getSum() { return sum; }
}This class is very similar to one that inherits from Thread. Imagine
for a moment that the code following Summer is extends Thread
instead of implements Runnable. The key thing a class derived from
Thread needs is an overridden run() method. Since only the run()
method is important, the designers of Java provided a way to create a
thread using the Runnable interface. To implement this interface, only
a public void run() method is required.
When creating a new thread, there are some differences in syntax between
the two styles. The familiar way of creating and running a thread from a
Thread subclass is as follows.
Summer summer = new Summer(array, lower, upper);
summer.start();Since Summer doesn’t inherit from Thread, it doesn’t have a
start() method, and this code won’t compile. When a class only
implements Runnable, it’s still necessary to create a Thread object
and call its start() method. Thus, an extra step is needed.
Summer summer = new Summer(array, lower, upper);
Thread thread = new Thread(summer);
thread.start();This alternate way of implementing the Runnable interface seems more
cumbersome than inheriting directly from Thread, since you have to
instantiate a separate Thread object. However, most developers prefer
to design classes that implement Runnable instead of inheriting from
Thread. Why? Java only allows for single inheritance. If your class
implements Runnable, it’s free to inherit from another parent class
with features you might want.
In domain decomposition, we often need to create multiple threads, all from the same class. As an example, consider the following thread declaration.
public class NumberedThread extends Thread {
private int value;
public NumberedThread(int input) { value = input; }
public void run() {
System.out.println("Thread " + value);
}
}Now, suppose we want to create 10 thread objects of type
NumberedThread, start them, and then wait for them to complete.
NumberedThread[] threads = new NumberedThread[10]; (1)
for(int i = 0; i < threads.length; i++) {
threads[i] = new NumberedThread(i); (2)
threads[i].start(); (3)
}
try {
for(int i = 0; i < threads.length; i++)
threads[i].join(); (4)
}
catch(InterruptedException e) {
System.out.println("A thread didn't finish!");
}| 1 | First, we declare an array to hold references to NumberedThread
objects. Like any other type, we can make an array to hold objects that
inherit from Thread. |
| 2 | The first line of the for loop instantiates a
new NumberedThread object, invoking the constructor which stores the
current iteration of the loop into the value field. The reference to
each NumberedThread object is stored in the array. Remember that the
constructor does not start a new thread running. |
| 3 | The second line of the for loop does that. |
| 4 | We’re also interested in when the threads stop. Calling the join()
method forces the main thread to wait for each thread to finish. |
The entire second for loop is nested inside of a try block. If the
main thread is interrupted while waiting for any of the threads to
finish, an InterruptedException will be caught. As before, we warn the
user that a thread didn’t finish. For production-quality code, the
catch block should handle the exception in such a way that the thread
can recover and do useful work even though it didn’t get what it was
waiting for.
13.5. Examples: Concurrency and speedup
Speedup is one of the strongest motivations for writing concurrent programs. To understand speedup, let’s assume we have a problem to solve. We write two programs to solve this problem, one that’s sequential and another that’s concurrent and, hence, able to exploit multiple cores. Let ts be the average time to execute the sequential program and tc the average time to execute the concurrent program. So that the comparison is meaningful, assume that both programs are executed on the same computer. The speedup obtained from concurrent programming is defined as ts/tc.
Speedup measures how much faster the concurrent program executes relative to the sequential program. Ideally, we expect tc < ts, making the speedup greater than 1. However, simply writing a concurrent program doesn’t guarantee that it’s faster than the sequential version.
To determine speedup, we need to measure ts and
tc. Time in a Java program can easily be measured with
the following two static methods in the System class.
public static long currentTimeMillis()
public static long nanoTime()The first of these methods returns the current time in milliseconds
(ms). A millisecond is 0.001 seconds. This method gives the difference
between the current time on your computer’s clock and midnight of
January 1, 1970 Coordinated Universal Time (UTC). This point in time is
used for many timing features on many computer platforms and is called
the Unix epoch. The other method returns the current time in
nanoseconds (ns). A nanosecond is 0.000000001 or 10-9 seconds. This method also
gives the difference between the current time and some fixed time, which
is system dependent and not necessarily the Unix epoch. The
System.nanoTime() method can be used when you want timing precision
finer than milliseconds; however, the level of accuracy it returns is
again system dependent. The next example show how to use these methods
to measure execution time.
Suppose we want to measure the execution time of a piece of Java code.
For convenience, we can assume this code is contained in the work()
method. The following code snippet measures the time to execute
work().
long start = System.currentTimeMillis();
work();
long end = System.currentTimeMillis();
System.out.println("Elapsed time: " + (end - start) + " ms");The output will give the execution time for work() measured in
milliseconds. To get the execution time in nanoseconds, use the
System.nanoTime() method instead.
Now that we have the tools to measure execution time, we can measure speedup. The next few examples show the speedup (or lack of it) that we can achieve using a concurrent solution to a few simple problems.
Recall the concurrent program in Example 13.6 to evaluate a simple mathematical expression. This program uses two threads. We executed this multi-threaded program on an iMac computer with an Intel Core 2 Duo running at 2.16 Ghz. The execution time was measured at 1,660,000 nanoseconds. We also wrote a simple sequential program to evaluate the same expression. It took 4,100 nanoseconds to execute this program on the same computer. Plugging in these values for tc and ts, we can find the speedup.

This speedup is much less than 1. Although this result might be surprising, the concurrent program with two threads executes slower than the sequential program. In this example, the cost of creating, running, and joining threads outweighs the benefits of concurrent calculation on two cores.
In Example 13.3, we introduced the problem of applying a function to every value in an array and then summing the results. Let’s say that we want to apply the sine function to each value. To solve this problem concurrently, we partition the array evenly among a number of threads, using the domain decomposition strategy. Each thread finds the sum of the sines of the values in its part of the array. One factor that determines whether or not we achieve speedup is the complexity of the function, in this case sine, that we apply. Although we may achieve speedup with sine, a simpler function such as doubling the value might not create enough work to justify the overhead of using threads.
We create class SumThread whose run() method sums the sines of those
elements of the array in its assigned partition.
import java.util.Random;
public class SumThread extends Thread {
private double sum = 0.0; (1)
private int lower;
private int upper;
private double[] array; (2)
public static final int SIZE = 1000000; (3)
public static final int THREADS = 8;
public SumThread(double[] array, int lower, int upper) { (4)
this.array = array;
this.lower = lower;
this.upper = upper;
}| 1 | First, we set up all the fields that the class will need. |
| 2 | Note that every SumThread object will have its own reference to the array of data. |
| 3 | We fix the array size at 1,000,000 and the number of threads at 8, but these values could easily be changed or read as input instead. |
| 4 | In its constructor, a SumThread takes a reference to the array of data
and the lower and upper bounds of its partition. Like most
ranges we discuss, the lower bound is inclusive though the upper bound
is exclusive. |
public void run() {
for(int i = lower; i < upper; i++)
sum += Math.sin(array[i]); (1)
}
public double getSum() { return sum; } (2)| 1 | In the for loop of the run() method, the SumThread finds the sine
of each number in its array partition and adds that value to its running
sum. |
| 2 | The getSum() method is an accessor that allows the running sum to
be retrieved. |
public static void main(String[] args) {
double[] data = new double[SIZE]; (1)
Random random = new Random();
int start = 0;
for(int i = 0; i < SIZE; i++) (2)
data[i] = random.nextDouble();
SumThread[] threads = new SumThread[THREADS];
int quotient = data.length / THREADS;
int remainder = data.length % THREADS;
for(int i = 0; i < THREADS; i++) {
int work = quotient;
if(i < remainder)
work++;
threads[i] = new SumThread(data, start, start + work); (3)
threads[i].start(); (4)
start += work;
} | 1 | The main() method begins by instantiating the array. |
| 2 | It fills it with random values. |
| 3 | Then, each thread is created by passing in a reference to the array and lower and upper bounds that mark the thread’s partition of the array. If the process using the array length and the number of threads to determine upper and lower bounds doesn’t make sense, refer to Section 6.11 which describes the fair division of work to threads. If the length of the array is not divisible by the number of threads, simple division isn’t enough. |
| 4 | After each thread is created, its start() method is called. |
double sum = 0.0; (1)
try {
for(int i = 0; i < THREADS; i++) {
threads[i].join(); (2)
sum += threads[i].getSum(); (3)
}
System.out.println("Sum: " + threads[0].getSum()); (4)
}
catch(InterruptedException e) {
e.printStackTrace(); (5)
}
}
}| 1 | Once the threads have started working, the main thread creates its own running total. |
| 2 | It iterates through each thread waiting for it to complete. |
| 3 | When each thread is done, its value is added to the running total. |
| 4 | Finally, the sum is printed out. |
| 5 | If the main thread is interrupted while waiting for a thread to complete, the stack trace is printed. |
In Example 13.4, we discussed the importance of matrix operations in many applications. Now that we know the necessary Java syntax, we can write a concurrent program to multiply two square matrices A and B and compute the resultant matrix C. If these matrices have n rows and n columns, the value at the ith row and jth column of C is

In Java, it’s natural for us to store matrices as 2-dimensional arrays.
To do this multiplication sequentially, the simplest approach uses three
nested for loops. The code below is a direct translation of the
mathematical notation, but we do have to be careful about bookkeeping.
Note that mathematical notation often uses uppercase letters to
represent matrices though the Java convention is to start all variable
names with lowercase letters.
for(int i = 0; i < c.length; i++)
for(int j = 0; j < c[i].length; j++)
for(int k = 0; k < b.length; k++)
c[i][j] += a[i][k] * b[k][j];The first step in making a concurrent solution to this problem is to
create a Thread subclass which will do some part of the matrix
multiplication. Below is the MatrixThread class which will compute a
number of rows in the answer matrix c.
public class MatrixThread extends Thread {
private double[][] a;
private double[][] b;
private double[][] c;
private int lower;
private int upper;
public MatrixThread(double[][] a, double[][] b, (1)
double[][] c, int lower, int upper) {
this.a = a;
this.b = b;
this.c = c;
this.lower = lower;
this.upper = upper;
}
public void run() { (2)
for(int i = lower; i < upper; i++)
for(int j = 0; j < c[i].length; j++)
for(int k = 0; k < b.length; k++)
c[i][j] += a[i][k] * b[k][j];
}
}| 1 | The constructor for MatrixThread stores references to the arrays
corresponding to matrices A, B, and
C as well as lower and upper bounds on the rows of
C to compute. |
| 2 | The body of the run() method is identical
to the sequential solution except that its outermost loop runs only from
lower to upper instead of through all the rows of the result. It’s
critical that each thread is assigned a set of rows that does not
overlap with the rows another thread has. Not only would having multiple
threads compute the same row be inefficient, it would very likely lead
to an incorrect result, as we’ll see in
Chapter 14. |
The following client code uses an array of MatrixThread objects to
perform a matrix multiplication. We assume that an int constant named
THREADS has been defined which gives the number of threads we want to
create.
MatrixThread[] threads = new MatrixThread[THREADS];
int quotient = c.length / THREADS;
int remainder = c.length % THREADS;
int start = 0;
for(int i = 0; i < THREADS; i++) {
int rows = quotient;
if(i < remainder)
rows++;
threads[i] = new MatrixThread(a, b, c, start, start + rows); (1)
threads[i].start(); (2)
start += rows;
}
try {
for(int i = 0; i < THREADS; i++) (3)
threads[i].join();
}
catch(InterruptedException e) {
e.printStackTrace();
}| 1 | We loop through the array, creating a MatrixThread object for each
location. As in the previous example, we use the approach described in
Section 6.11 to allocate rows to each thread fairly.
Each new MatrixThread object is given a reference to each of the three
matrices as well as an inclusive starting and an exclusive ending row. |
| 2 | After the MatrixThread objects are created, we start them running with
the next line of code. |
| 3 | Next, there’s a familiar for loop with the join() calls that force
the main thread to wait for the other threads to finish. |
Presumably,
code following this snippet will print the values of the result matrix
or use it for other calculations. If we didn’t use the join()
calls to be sure the threads have finished, we might print out a result
matrix that’s only been partially filled in.
We completed the code for threaded matrix multiplication and executed it on an iMac computer with an Intel Core 2 Duo running at 2.16 Ghz. The program was executed for matrices of different sizes (n × n). For each size, the sequential and concurrent execution times in seconds and the corresponding speedup are listed in the following table.
| Size (n) | ts (s) | tc (s) | Speedup |
|---|---|---|---|
100 |
0.013 |
0.9 |
0.014 |
500 |
1.75 |
4.5 |
0.39 |
1,000 |
15.6 |
10.7 |
1.45* |
Only with 1,000 × 1,000 matrices did we see improved performance when using two threads. In that case, we achieved a speedup of 1.45, marked with an asterisk. In the other two cases, performance became worse.
13.6. Concepts: Thread scheduling
Now that we’ve seen how multiple threads can be used together, a number of questions arise: Who decides when these threads run? How is processor time shared between threads? Can we make any assumptions about the order in which the threads run? Can we affect this order?
These questions focus on thread scheduling. Because different concurrent systems handle scheduling differently, we’ll only describe scheduling in Java. Although sequential programming is all about precise control over what happens next, concurrency takes much of this control away from the programmer. When threads are scheduled and which processor they run on is handled by a combination of the JVM and the OS. With normal JVMs, there’s no explicit way to access the scheduling and alter it to your liking.
Of course, there are a number of implicit ways a programmer can affect scheduling. In Java, as in several other languages and programming systems, threads have priorities. Higher priority threads run more often than lower priority threads. Some threads are performing mission-critical operations which must be carried out as quickly as possible, and some threads are just doing periodic tasks in the background. A programmer can set thread priorities accordingly.
Setting priorities gives only a very general way of controlling which
thread will run. The threads themselves might have more specific
information about when they will and won’t need processor time. A
thread may need to wait for a specific event and won’t need to run
until then. Java allows threads to interact with the scheduler through
Thread.sleep() and Thread.yield(), which we’ll discuss in
Section 13.7, and through the wait(), method which
we’ll discuss in Chapter 14.
13.6.1. Nondeterminism
In Java, the mapping of a thread inside the JVM to a thread in the OS varies. Some implementations give each Java thread an OS thread, some put all Java threads on a single OS thread (with the side effect of preventing parallel execution), and some allow for the possibility of changing which OS thread a Java thread uses. Thus, the performance and, in some cases, the correctness of your program might vary, depending on which system you’re running. This is, yet again, one of those times when Java is platform independent…but not entirely.
Unfortunately, the situation is even more complicated. Making threads part of your program means that the same program could run differently on the same system. The JVM and the OS have to cooperate to schedule threads, and both programs are complex mountains of code which try to balance many factors. If you create three threads, there’s no guarantee that the first will run first, the second second, and the third third, even if it happens that way the first 10 times you run the program. Exercise 13.18 shows that the pattern of thread execution can vary a lot.
In all the programs before this chapter, the same sequence of input would always produce the same sequence of output. Perhaps the biggest hurdle created by this nondeterminism is that programmers must shift their paradigm considerably. The processor can switch between executions of threads at any time, even in the middle of operations. Every possible interleaving of thread execution could crop up at some point. Unless you can be sure that your program behaves properly for all of them, you might never be able to debug your code completely. What’s so insidious about nondeterministic bugs is that they can occur rarely and be almost impossible to reproduce. In this chapter, we’ve introduced how to create and run threads, but making these threads interact properly is a major problem we tackle in subsequent chapters.
After those dire words of warning, we’d like to remind you that nondeterminism is not in itself a bad thing. Many threaded applications with a lot of input and output, such as server applications, necessarily exist in a nondeterministic world. For these programs, many different sequences of thread execution may be perfectly valid. Each individual program may have a different definition of correctness. For example, if a stock market server receives two requests to buy the last share of a particular stock at almost the same time from two threads corresponding to two different clients, it might be correct for either one of them to get that last share. However, it would never be correct for both of them to get it.
13.6.2. Polling
So far the only mechanism we’ve introduced for coordinating different
threads is using the join() method to wait for a thread to end.
Another technique is polling, or busy waiting. The idea is to keep
checking the state of one thread until it changes.
There are a number of problems with this approach. The first is that it wastes CPU cycles. Those cycles spent by the waiting thread continually checking could have been used productively by some other thread in the system. The second problem is that we have to be certain that the state of the thread we’re waiting for won’t change back to the original state or to some other state. Because of the unpredictability of scheduling, there’s no guarantee that the waiting thread will read the state of the other thread when it has the correct value.
We bring up polling partly because it has a historical importance to parallel programming, partly because it can be useful in solving some problems in this chapter, and partly because we want you to understand the reasons why we need better techniques for thread communication.
13.7. Syntax: Thread states
A widely used Java tool for manipulating scheduling is the
Thread.sleep() method. This method can be called any time you want a
thread to do nothing for a set period of time. Until the sleep timer
expires, the thread will not be scheduled for any CPU time, unless it’s
interrupted. To make a thread of execution sleep, call Thread.sleep()
in that thread of execution with a number of milliseconds as a
parameter. For example, calling Thread.sleep(2000) will make the
calling thread sleep for two full seconds.
Another useful tool is the Thread.yield() method. It gives up use of
the CPU so that the next waiting thread can run. To use it, a thread
calls Thread.yield(). This method is useful in practice, but
according to official documentation, the JVM doesn’t have to do to
anything when a Thread.yield() call happens. The Java specification
doesn’t demand a particular implementation. A JVM could ignore a
Thread.yield() call completely, but most JVMs will move on to the next
thread in the schedule.

Figure 13.7 shows the lifecycle of a thread. A
thread begins its life in the New Thread state, after the constructor is
called. When the start() method is called, the thread begins to run
and transitions to the Runnable state. Being Runnable doesn’t
necessarily mean that the thread is executing at any given moment but
that it’s ready to run at any time. When in the Runnable state, a
thread may call Thread.yield(), relinquishing use of the processor,
but it will still remain Runnable.
However, if a thread goes to sleep with a Thread.sleep() call, waits
for a condition to be true using a wait() call, or performs a blocking
I/O operation, the thread will transition to the Not Runnable state. Not
Runnable threads cannot be scheduled for processor time until they wake
up, finish waiting, or complete their I/O. The final state is
Terminated. A thread becomes Terminated when its run() method
finishes. A Terminated thread cannot become Runnable again and is no
longer a separate thread of execution.
Any object with a type that’s a subclass of Thread can tell you its
current state using the getState() method. This method returns an
enum type, whose value must come from a fixed list of constant
objects. These objects are Thread.State.NEW, Thread.State.RUNNABLE,
Thread.State.BLOCKED, Thread.State.WAITING,
Thread.State.TIMED_WAITING, and Thread.State.TERMINATED. Although
the others are self explanatory, we lump the Thread.State.BLOCKED,
Thread.State.WAITING, and Thread.State.TIMED_WAITING values into
the Not Runnable state, since the distinction between the three isn’t
important for us.
Threads also have priorities in Java. When an object that’s a subclass
of Thread is created in Java, its priority is initially the same as
the thread that creates it. Usually, this priority is
Thread.NORM_PRIORITY, but there are some special cases when it’s a
good idea to raise or lower this priority. Avoid changing thread
priorities because it increases platform dependence and because the
effects are not always predictable. Be aware that priorities exist, but
don’t use them unless and until you have a good reason.
Let’s apply the ideas discussed above to a lighthearted example. You
might be familiar with sound of soldiers marching: “Left, Left, Left,
Right, Left!” We can design a thread that prints Left and another
thread that prints Right. We can combine the two to print the correct
sequence for marching and loop the whole thing 10 times so that we can
see how accurately we can place the words. We want to use the scheduling tools
discussed above to get the timing right. Let’s try Thread.sleep()
first.
public class LeftThread extends Thread {
public void run() {
for(int i = 0; i < 10; i++) {
System.out.print("Left "); (1)
System.out.print("Left ");
System.out.print("Left ");
try { Thread.sleep(10); } (2)
catch(InterruptedException e) {
e.printStackTrace();
}
System.out.println("Left"); (3)
}
}
}| 1 | Inside, the for loop, this thread prints out Left three times. |
| 2 | The, it waits for 10 milliseconds. |
| 3 | Finally, it prints out Left again and repeats the loop. |
public class RightThread extends Thread {
public void run() {
try {
Thread.sleep(5); (1)
for(int i = 0; i < 10; i++) {
System.out.print("Right "); (2)
Thread.sleep(10); (3)
}
}
catch(InterruptedException e) {
e.printStackTrace();
}
}
}| 1 | This thread waits for 5 milliseconds to get synchronized. |
| 2 | Inside its for loop, it prints out Right. |
| 3 | Then, it waits for 10 milliseconds and repeats the loop. |
The driver program below creates a thread for each of these
classes and then starts them. If you run this program, you should see 10
lines of Left Left Left Right Left, but there are a few problems.
public class MilitaryMarching {
public static void main(String[] args) {
LeftThread left = new LeftThread();
RightThread right = new RightThread();
left.start();
right.start();
try {
left.join();
right.join();
}
catch(InterruptedException e) {
e.printStackTrace();
}
}
}The first problem is that we have to wait some amount of time between
calls. We could shorten the Thread.sleep() calls, but there are limits
on the resolution of the timer. The bigger problem is that the two
threads can sometimes get out of sync. If you run the program many
times, you might see a Right out of place once in a while. If you
increase the repetitions of the for loops to a larger number, the
errors will become more likely. Whether or not you see errors is somewhat system
dependent. We can try Thread.yield() instead of Thread.sleep().
public class LeftYieldThread extends Thread {
public void run() {
for(int i = 0; i < 10; i++) {
System.out.print("Left ");
System.out.print("Left ");
System.out.print("Left ");
Thread.yield();
System.out.println("Left");
}
}
}public class RightYieldThread extends Thread {
public void run() {
for(int i = 0; i < 10; i++) {
System.out.print("Right ");
Thread.yield();
}
}
}These new versions of the two classes have essentially replaced calls to
Thread.sleep() with calls to Thread.yield(). Without the need for
exception handling, the code is simpler, but we’ve traded one set of
problems for another. If there are other threads operating in the same
application, they’ll be scheduled in ways that will interfere with the
pattern of yielding. If you’re running this code on a machine
with a single processor and a single core, you have a good chance of
seeing something which matches the expected output. However, if you’re running
it on multiple cores, everything will be jumbled. It’s likely that
the LeftYieldThread will be running on one processor with the
RightYieldThread on another. In that case, neither has any competition
to yield to.
Finally, let’s look at a polling solution which still falls short of the mark. To do this, we need state variables inside of each class to keep track of whether or not it’s done. Each thread needs a reference to the other thread to make queries, and the driver program must be updated to add these in before starting the threads.
public class LeftPollingThread extends Thread {
private RightPollingThread right;
private boolean done = false;
public void setRight(RightPollingThread right) {
this.right = right;
}
public void run() {
for(int i = 0; i < 10; i++) {
System.out.print("Left ");
System.out.print("Left ");
System.out.print("Left ");
done = true;
while(!right.isDone());
right.setDone(false);
System.out.println("Left");
}
}
public boolean isDone() { return done; }
public void setDone(boolean value) { done = value; }
}public class RightPollingThread extends Thread {
private LeftPollingThread left;
private boolean done = false;
public void setLeft(LeftPollingThread left) {
this.left = left;
}
public void run() {
for(int i = 0; i < 10; i++) {
while(!left.isDone());
left.setDone(false);
System.out.print("Right ");
done = true;
}
}
public boolean isDone() { return done; }
public void setDone(boolean value) { done = value; }
}Whether single core or multicore, this solution will always give the
right output. Or it should. Java experts will point out that we are
violating a technicality of the Java Memory Model. Because we’re not
using synchronization tools, we have no guarantee that the change of the
done variable will even be visible from one thread to another. In
practice, this problem should affect you rarely, but to be safe, both of
the done variables should be declared with the keyword volatile.
This keyword makes Java aware that the value may be accessed at any time
from arbitrary threads.
Another issue is that there’s no parallel execution. Each thread must wait
for the other to complete. Of course, this problem does not benefit from
a parallelism, but applying this solution to problems which can
benefit from parallelism might cause performance problems. Each thread
wastes time busy waiting in a while loop for the other to be done,
consuming CPU cycles while it does so. You’ll notice that the code
must still be carefully written. Each thread must set the other thread’s
done value to false. If threads were responsible for setting their
own done values to false, one thread might print its information and
go back to the top of the for loop before the other thread had reset
its own done to false.
In short, coordinating two or more threads together is a difficult problem. None of the solutions we give here are fully acceptable. We introduce better tools for coordination and synchronization in Chapter 14.
13.8. Solution: Deadly virus
Finally, we give the solution to the deadly virus problem. By this
point, the threaded part of this problem should not seem very difficult.
It’s simpler than some of the examples, such as matrix multiplication.
We begin with the worker class FactorThread that can be spawned as a
thread.
public class FactorThread extends Thread {
private long lower;
private long upper;
public FactorThread(long lower, long upper) {
this.lower = lower;
this.upper = upper;
}
public void run() {
if(lower % 2 == 0) // Only check odd numbers
lower++;
while(lower < upper) {
if(Factor.NUMBER % lower == 0) {
System.out.println("Security code: " + (lower + Factor.NUMBER / lower));
return;
}
lower += 2;
}
}
}The constructor for FactorThread takes an upper and lower bound,
similar to MatrixThread. Once a FactorThread object has those
bounds, it can search between them. The number to factor is stored in
the Factor class. If any value divides that number evenly, it must be
one of the factors, making the other factor easy to find, sum, and print
out. We have to add a couple of extra lines of code to make sure that we
only search the odd numbers in the range. This solution is tuned for
efficiency for this specific security problem. A program to find general
prime factors would have to be more flexible. Next, let’s examine the
driver program Factor.
public class Factor {
public static final int THREADS = 4; (1)
public static final long NUMBER = 59984005171248659L;
public static void main(String[] args) {
FactorThread[] threads = new FactorThread[THREADS]; (2)
long root = (long)Math.sqrt(NUMBER); // Go to square root
long start = 3; // No need to test 2
long quotient = root / THREADS;
long remainder = root % THREADS;
for(int i = 0; i < THREADS; i++) {
long work = quotient;
if(i < remainder)
work++;
threads[i] = new FactorThread(start, start + work); (3)
threads[i].start();
start += work;
}
try {
for(int i = 0; i < THREADS; i++)
threads[i].join(); (4)
}
catch(InterruptedException e) {
e.printStackTrace();
}
}
}| 1 | Static constants hold both the number to be factored and the number of threads. |
| 2 | In the main() method, we create an array of threads for
storage. |
| 3 | Then, we create and start each FactorThread object, assigning upper and
lower bounds at the same time, using the standard technique from
Section 6.11 to divide the work fairly. Because we
know the number we’re dividing isn’t even, we start with 3. By only
going up to the square root of the number, we know that we will only
find the smaller of the two factors. In that way we can avoid having one
thread find the smaller while another is finds the larger. |
| 4 | Afterward, we have the usual join() calls to make sure that all the
threads are done. In this problem, these calls are unnecessary. One
thread will print out the correct security code, and the others will
search fruitlessly. If the program went on to do other work, we might
need to let the other threads finish or even interrupt them. Don’t
forget join() calls since they’re usually very important. |
13.9. Summary
In this chapter we’ve explored two strategies to obtain a concurrent solution to programming problems. One strategy, task decomposition, splits a task into two or more subtasks. These subtasks can then be packaged as Java threads and executed on different cores of a multicore processor. Another strategy, domain decomposition, partitions input data into smaller chunks and allows different threads to work concurrently on each chunk of data.
A concurrent solution to a programming problem can sometimes execute more quickly than a sequential solution. Speedup measure how effective a concurrent solution is at exploiting the architecture of a multicore processor. Note that not all concurrent programs lead to speedup as some run slower than their sequential counterparts. Writing a concurrent program is a challenge that forces us to divide up work and data in a way that best exploits the available processors and OS.
Java provides a rich set of primitives and syntactic elements to write concurrent programs, but only a few of these were introduced in this chapter. Subsequent chapters give additional tools to code more complex concurrent programs.
13.10. Exercises
Conceptual Problems
-
The
start(),run(), andjoin()methods are essential parts of the process of using threads in Java. Explain the purpose of each method. -
What’s the difference between extending the
Threadclass and implementing theRunnableinterface? When should you use one over the other? -
How do the
Thread.sleep()method and theThread.yield()method each affect thread scheduling? -
Consider the expression in Example 13.2. Suppose that the multiply and exponentiation operations require 1 and 10 time units, respectively. Compute the number of time units required to evaluate the expression as in Figure 13.2(a) and (b).
-
Suppose that a computer has one quad-core processor. Can the tasks in Example 13.1 and Example 13.2 be further subdivided to improve performance on four cores? Why or why not?
-
Consider the definition of speedup from Section 13.5. Let’s assume you have a job 1,000,000 units in size. A thread can process 10,000 units of work every second. It takes an additional 100 units of work to create a new thread. What’s the speedup if you have a dual-core processor and create 2 threads? What if you have a quad-core processor and create 4 threads? Or an 8-core processor and create 8 threads? You may assume that a thread does not need to communicate after it’s been created.
-
In which situations can speedup be smaller than the number of processors? Is it ever possible for speedup to be greater than the number of processors?
-
Amdahl’s Law is a mathematical description of the maximum amount you can improve a system by only improving a part of it. One form of it states that the maximum speedup attainable in a parallel program is 1/(1 - P) where P is the fraction of the program which can be parallelized to an arbitrary degree. If 30% of the work in a program can be fully parallelized but the rest is completely serial, what’s the speedup with two processors? Four? Eight? What implications does Amdahl’s Law have?
-
Consider the following table of tasks:
Task Time Concurrency Dependency Washing Dishes
30
3
Cooking Dinner
45
3
Washing Dishes
Cleaning Bedroom
10
2
Cleaning Bathroom
30
2
Doing Homework
30
1
Cleaning Bedroom
In this table, the Time column gives the number of minutes a task takes to perform with a single person, the Concurrency column gives the maximum number of people who can be assigned to a task, and the Dependency column shows which tasks can’t start until other tasks have been finished. Assume that people assigned to a given task can perfectly divide the work. In other words, the time a task takes is the single person time divided by the number of people assigned. What’s the minimum amount of time needed to perform all tasks with only a single person? What is the minimum amount of time needed to perform all tasks with an unlimited number of people? What’s the smallest number of people needed to achieve this minimum time?
-
Consider the following code snippet.
x = 13; x = x * 10;Consider this snippet as well.
x = 7; x = x + x;If we assume that these two snippets of code are running on separate threads but that
xis a shared variable, what are the possible valuesxcould have after both snippets have run? Remember that the execution of these snippets can be interleaved in any way.
Programming Practice
-
Re-implement the array summing problem from Example 13.10 using polling instead of
join()calls. Your program should not use a single call tojoin(). Polling is not an ideal way to solve this problem, but it’s worth thinking about the technique. -
Composers often work with multiple tracks of music. One track might contain solo vocals, another drums, a third one violins, and so on. After recording the entire take, a mix engineer might want to apply special effects such as an echo to one or more tracks.
To understand how to add echo to a track, suppose that the track consists of a list of audio samples. Each sample in a mono (not stereo) track can be stored as a
doublein an array. To create an echo effect, we combine the current value of an audio sample with a sample from a fixed time earlier. This time is called the delay parameter. Varying the delay can produce long and short echoes.If the samples are stored in array
inand the delay parameter is stored in variabledelay(measured in number of samples), the following code snippet can be used to create arrayoutwhich contains the sound with an echo.double[] out = new double[in.length + delay]; // Sound before echo starts for(int i = 0; i < delay; i++) out[i] = in[i]; // Sound with echo for(int i = delay; i < in.length; i++) out[i] = a*in[i] + b*in[i - delay]; // Echo after sound is over for(int i = in.length; i < out.length; i++) out[i] = b*in[i - delay];Parameters
aandbare used to control the nature of the echo. Whenais1andbis0, there is no echo. Whenais0andbis1, there is no mixing. Audio engineers will control the values ofaandbto create the desired echo effect.Write a threaded program that computes the values in
outin parallel for an arbitrary number of threads. -
Write a program which takes a number of minutes and seconds as input. In this program, implement a timer using
Thread.sleep()calls. Each second, print the remaining time to the screen. How accurate is your timer? -
As you know, π ≈ 3.1416. A more precise value can be found by writing a program which approximates the area of a circle. The area of a circle can be approximated by summing up the area of rectangles filling curve of the arc of the circle. As the width of the rectangle goes to zero, the approximation becomes closer and closer to the true area. If a circle with radius r is centered at the origin, its height y at a particular distance x is given by the following formula.
Write a parallel implementation of this problem which divides up portions of the arc of the circle among several threads and then sums the results after they all finish. By setting r = 2, you need only sum one quadrant of a circle to get π. You’ll need to use a very small rectangle width to get an accurate answer. When your program finishes running, you can compare your value against
Math.PIfor accuracy.
Experiments
-
Use the
currentTimeMillis()method to measure the time taken to execute a relatively long-running piece of Java code you’ve written. Execute your program several times and compare the execution time you obtain during different executions. Why do you think the execution times are different? -
Thread creation overhead is an important consideration in writing efficient parallel programs. Write a program which creates a large number of threads which do nothing. Test how long it takes to create and join various numbers of threads. See if you can determine how long a single thread creation operation takes on your system, on average.
-
Create serial and concurrent implementations of matrix multiplication like those described in Example 13.11.
-
Experiment with different matrix sizes and thread counts to see how the speedup performance changes. If possible, run your tests on machines with different numbers of cores or processors.
-
Given a machine with k > 1 cores, what is the maximum speedup you can expect to obtain?
-
-
Repeatedly run the code in Example 13.7 which creates several
NumberedThreadobjects. Can you discover any patterns in the order that the threads print? Add a loop and some additional instrumentation to theNumberedThreadclass which will allow you to measure how long each thread runs before the next thread has a turn. -
Create serial and parallel implementations of the array summing problem solved in Example 13.10. Experiment with different array sizes and thread counts to see how performance changes. How does the speedup differ from matrix multiply? What happens if you simply sum the numbers instead of taking the sine first?
-
The solution to the array summing problem in Example 13.10 seems to use concurrency half-heartedly. After all the threads have computed their sums, the main thread sums up the partial sums sequentially.
An alternative approach is to sum up the partial sums concurrently. Once a thread has computed the sum of the sines of each partition, the sums of each pair of neighboring partitions should be merged into a single sum. The process can be repeated until the final sum has been computed. At each step, half of the remaining threads will have nothing left to do and will stop. The pattern of summing is like a tree which starts with k threads working at the first stage, k/2 working at the second stage, k/4 working at the third, and so on, until a single thread completes the summing process.
Figure 13.8 Example of concurrent tree-style summation with 8 threads.Update the
run()method in theSumThreadclass so that it adds its assigned elements as before and then adds its neighbor’s sum to its own. To do so, it must use thejoin()method to wait for the neighboring thread. It should perform this process repeatedly. After summing their own values, each even numbered thread should add in the partial sum from its neighbor. At the next step, each thread with a number divisible by 4 should add the partial sum from its neighbor. At the next step, each thread with a number divisible by 8 should add the partial sum from its neighbor, and so on. Thread 0 will perform the final summation. Consequently, the main thread only needs to wait for thread 0. So that each thread can wait for other threads, thethreadsarray will need to be a static field. Figure 13.8 illustrates this process.Once you’ve implemented this design, test it against the original
SumThreadclass to see how it performs. Restrict the number of threads you create to a power of 2 to make it easier to determine which threads wait and which threads terminate.
14. Synchronization
Sharing is sometimes more demanding than giving.
14.1. Introduction
Concurrent programs allow multiple threads to be scheduled and executed, but the programmer doesn’t have a great deal of control over when threads execute. As explained in Section 13.6, the JVM and the underlying OS are responsible for scheduling threads onto processor cores.
While writing a concurrent program, you have to ensure that the program will work correctly even though different executions of the same program will likely lead to different sequences of thread execution. The problem we introduce next illustrates why one thread execution sequence might be perfectly fine while another might lead to unexpected and incorrect behavior. (And even people starving!)
14.2. Problem: Dining philosophers
Concurrency gives us the potential to make our programs faster but introduces a number of other problems. The way that threads interact can be unpredictable. Because they share memory, one thread can corrupt a value in another thread’s variables. We introduce synchronization tools in this chapter that can prevent threads from corrupting data, but these tools create new pitfalls. To explore these pitfalls, we give you another problem to solve.
Imagine a number of philosophers sitting at a round table with plates that are periodically filled with rice. Between adjacent philosophers are single chopsticks so that there are exactly the same number of chopsticks as there are philosophers. These philosophers only think and eat. In order to eat, a philosopher must pick up both the chopstick on her left and the chopstick on her right. Figure 14.1 illustrates this situation.

Your goal is to write a class called DiningPhilosopher which extends
Thread. Each thread created in the main() method should be a
philosopher who thinks for some random amount of time, then acquires the
two necessary chopsticks and eats. No philosopher should starve. No
philosophers should be stuck indefinitely fighting over chopsticks.
Although this problem sounds simple, the solution is not. Make sure that you understand the concepts and Java syntax in this chapter thoroughly before trying to implement your solution. It’s important that no two philosophers try to use the same chopstick at the same time. Likewise, we need to avoid a situation where every philosopher is waiting for every other philosopher to give up a chopstick.
14.3. Concepts: Thread interaction
This dining philosopher problem highlights some difficulties which were emerging toward the end of the last chapter. In Exercise 13.10 two snippets of code could run concurrently and modify the same shared variable, potentially producing incorrect output. Because of the nondeterministic nature of scheduling, we have to assume that the code executing in two or more threads can be interleaved in any possible way. When the result of computation changes depending on the order of thread execution, it’s called a race condition. Below is a simple example of a race condition in Java.
public class RaceCondition extends Thread {
private static int counter = 0;
public static final int THREADS = 4;
public static final int COUNT = 1000000;
public static void main(String[] args) {
RaceCondition[] threads = new RaceCondition[THREADS];
for(int i = 0; i < THREADS; i++) {
threads[i] = new RaceCondition();
threads[i].start();
}
try {
for(int i = 0; i < THREADS; i++)
threads[i].join();
}
catch(InterruptedException e) {
e.printStackTrace();
}
System.out.println("Counter:\t" + counter);
}
public void run() {
for(int i = 0; i < COUNT/THREADS; i++)
counter++;
}
}This short (and pointless) class attempts to increment the variable
counter until it reaches 1000000. To illustrate the race condition,
we’ve divided the work of incrementing counter evenly among a number
of threads. If you run this program, the final value of counter will
often not be 1000000. Depending on which JVM, OS, and how many cores
you have, you may never get 1000000, and the answer you do get will
vary a lot. On all systems, if you change the value of THREADS to 1,
the answer should always be correct.
Looking at the code, the problem might not be obvious. Everything
centers on the statement counter++ in the for loop inside the
run() method. But, this statement appears to execute in a single step!
Each thread should increase the value of counter a total of
COUNT/THREADS times, adding up to 1000000. The trouble is that
counter++ is not a single step. Recall that counter++ is shorthand
for counter = counter + 1. To be even more explicit we could write it
as follows.
temp = counter;
counter = temp + 1;One thread might get as far as storing counter into a temporary
location, but then it runs out of time, allowing the next thread in the
schedule to run. When that’s the case, this next thread may do a series of
increments to count which are all overwritten when the first thread
runs again. Because the first thread had an old value of counter
stored in temp, adding 1 to temp has the effect of ignoring
increments that happened in the interim. This situation can happen on a single
processor with threads switching back and forth, but it’s even more dangerous
on a multicore system.
The primary lesson here is that threads can switch between each other at any time with unpredictable effects. The secondary lesson is that the source code is too coarse-grained to show atomic operations. An atomic operation is one which cannot be interrupted by a context switch to another thread. The actual code that the JVM runs is much lower level than source code.
We can’t easily force a non-atomic operation to be atomic, but there are
ways to restrict access to certain pieces of code under certain
conditions. The name we give to a piece of code which should not be
accessed by more than one thread at a time is a critical section. In
the example above, the single line of code which increments counter is
a critical section, and the error in the program would be removed if
only one thread were able to run that line of code at a time.
Protecting a critical section is done with mutual exclusion tools. They’re called mutual exclusion tools because they enforce the requirement that one thread executing a critical section excludes the possibility of another. There are many different techniques, algorithms, and language features in computer science which can be used to create mutual exclusion. Java relies heavily on a tool called a monitor which hides some of the details of enforcing mutual exclusion from the user. Mutual exclusion is a deeply researched topic with many approaches other than monitors. If you plan to write concurrent programs in another language, you may need to brush up on its mutual exclusion features.
14.4. Syntax: Thread synchronization
14.4.1. The synchronized keyword
In Java, the language feature which allows you to enforce mutual
exclusion is the synchronized keyword. There are two ways to use this
keyword: with a method or with an arbitrary block of code. In the method
version, you add the synchronized modifier before the return type.
Let’s imagine a class with a private String field called message
which is set to be "Will Robinson!" by the constructor. Now, we define
the following method.
public synchronized void danger() {
message = "Danger, " + message;
}If danger() is called five times from different threads, message
will contain
"Danger, Danger, Danger, Danger, Danger, Will Robinson!" Without the
synchronized keyword, danger() would suffer from a race condition
similar to the one in RaceCondition. Some of the String
concatenations might be overwritten by other calls to danger(). You
would never have more than five copies of "Danger, " appended to the
beginning of message, but you might have fewer.
Any time a thread enters a piece of code protected by the synchronized
keyword, it implicitly acquires a lock which only a single thread can
hold. If another thread tries to access the code, it’s forced to wait
until the lock is released. This lock is re-entrant. Re-entrant means
that, when a thread currently holds a lock and tries to get it again, it
succeeds. This situation frequently occurs with synchronized methods
which call other synchronized methods.
Consider method safety() which does the “opposite” of danger(), by
removing occurrences of "Danger, " from the beginning of message.
public synchronized void safety() {
if(message.startsWith("Danger, "))
message = message.substring(8);
}Will the danger() and safety() methods play nicely together on the
same object? In other words, will a thread be blocked from entering
safety() if another thread is already in danger()? Yes! The locks
in Java are connected to objects. When you use the synchronized keyword on a
method, the object the method is being called on (whichever object
this refers to inside the method) serves as the lock. Thus, only one
thread can be inside of either of these methods on a given object. If you have 10
synchronized methods in an object, only one of them can execute at a
time for that object.
Perhaps this level of control is too restrictive. You may have six
methods which conflict with each other and four others which conflict
with each other but not the first six. Using synchronized in each
method declaration would unnecessarily limit the amount of concurrency
your program could have.
Although it takes a little more work, using synchronized with a block
of code allows more fine-grained control. The following version of
danger() is equivalent to the earlier one.
public void danger() {
synchronized(this) {
message = "Danger, " + message;
}
}Using synchronized on a block of code gives us more flexibility in two
ways. First, we can choose exactly how much code we want to control,
instead of the whole method. Second, we can choose which object we want
to use for synchronization. For the block style, any arbitrary object
can be used as a lock. Objects keep a list of threads which are waiting
to get the lock and do all the other management needed to make the
synchronized keyword work.
If you have two critical sections which are unrelated to each other, you can use the fine-grained control the block style provides. First, you’ll need some objects to use as locks, probably declared so that they can easily be shared, perhaps as static fields of a class.
private static Object lock1 = new Object();
private static Object lock2 = new Object();Then, wherever you need control over concurrency, you use them as locks.
synchronized(lock1) {
// Do dangerous thing 1
}
// Do safe things
synchronized(lock2) {
// Do dangerous thing 2, unrelated to dangerous thing 1
}Since declaring a method with synchronized is equivalent to having its
body enclosed in a block beginning with synchronized(this), what about
static methods? Can they be synchronized? Yes, they can. Whenever a
class is loaded, Java creates an object of type Class which
corresponds to that class. This object is what synchronized static
methods inside the class will use as a lock. For example, a synchronized
static method inside of the Eggplant class will lock on the object
Eggplant.class.
14.4.2. The wait() and notify() methods
Protecting critical sections with the synchronized keyword is a
powerful technique, and many other synchronization tools can be built
using just this tool. However, efficiency demands a few more options.
Sometimes a thread is waiting for another thread to finish a task so
that it can process the results. Imagine one thread collecting votes
while another one’s waiting to count them. In this example, the
counting thread must wait for all votes to be cast before it can begin
counting. We could use a synchronized block and an indicator boolean
called votingComplete to allow the collector thread to signal to the
counting thread.
while(true) {
synchronized(this) {
if(votingComplete)
break;
}
}
countVotes();What’s the problem with this design? The counting thread is
running through the while loop over and over waiting for
votingComplete to become true. On a single processor, the counting
thread would slow down the job of the collecting thread which is trying
to process all the votes. On a multicore system, the counting thread is
still wasting CPU cycles that some other thread could use. This
phenomenon is known as busy waiting, for obvious reasons.
To combat this problem, Java provides the wait() method. When a thread’s
executing synchronized code, it can call wait(). Instead of busy
waiting, a thread which has called wait() will be removed from the
list of running threads. It will wait in a dormant state until someone
comes along and notifies the thread that its waiting is done. If you
recall the thread state diagram from Chapter 13,
there’s a Not Runnable state which threads enter by
calling sleep(), calling wait(), or performing blocking I/O. Using
wait(), we can rewrite the vote counting thread.
synchronized(this) {
while(!votingComplete) {
wait();
}
}
countVotes();Note that the while loop has moved inside the synchronized block.
Doing so before might have kept our program from terminating: As long as
the vote counting thread held the lock, the vote collecting thread would
not be allowed to modify votingComplete. When a thread calls wait(),
however, it gives up the corresponding lock it’s holding until it wakes
up and runs again. Why use the while loop at all now? There’s no
guarantee that the condition you’re waiting for is true. Many threads
might be waiting on this particular lock. We use the while loop to check
that votingComplete is true and wait again if it isn’t.
In order to notify a waiting thread, the other thread calls the
notify() method. Like wait(), notify() must be called within a
synchronized block or method. Here is corresponding code the vote
collecting thread might use to notify the counting thread that voting is
complete.
// Finish collecting votes
synchronized(this) {
votingComplete = true;
notifyAll();
}A call to notify() will wake up one thread waiting on the lock object.
If there are many threads waiting, the method notifyAll() used above
can be called to wake them all up. In practice, it’s usually safer to
call notifyAll(). If a particular condition changes and a single
waiting thread is notified, that thread might need to notify the next
waiting thread when it’s done. If your code isn’t very carefully
designed, some thread might end up waiting forever and never be notified
if you only rely on notify().
To illustrate the use of wait() and notify() calls inside of
synchronized code, we give a simple solution to the producer/consumer
problem below. This problem is a classic example in the concurrent
programming world. Often one thread (or a group of threads) is
producing data, perhaps from some input operation. At the same time, one
thread (or, again, a group of threads) is taking these chunks of
data and consuming them by performing some computational or output task.
Every resource inside of a computer is finite. Producer/consumer problems often assume a bounded buffer which stores items from the producer until the consumer can take them away. Our solution does all synchronization on this buffer. Many different threads can share this buffer, but all accesses will be controlled.
public class Buffer {
public final static int SIZE = 10;
private Object[] objects = new Object[SIZE];
private int count = 0;
public synchronized void addItem(Object object) throws InterruptedException { (1)
while(count == SIZE) (2)
wait();
objects[count] = object;
count++;
notifyAll(); (3)
}
public synchronized Object removeItem() throws InterruptedException { (4)
while(count == 0) (5)
wait();
count--;
Object object = objects[count];
notifyAll(); (6)
return object;
}
}| 1 | When adding an item, producers enter the synchronized addItem()
method. |
| 2 | If count shows that the buffer is full, the producer must wait
until the buffer has at least one open space. |
| 3 | After adding an item to the buffer, the producer then notifies all waiting threads. |
| 4 | The consumer
performs mirrored operations in removeItem(). |
| 5 | A consumer thread can’t consume anything if the buffer is empty and must then wait. |
| 6 | After there’s an object to consume, the consumer removes it and notifies all other threads. |
Both methods are synchronized, making access to the buffer completely sequential. Although it seems undesirable, sequential behavior is precisely what’s needed for the producer/consumer problem. All synchronized code is a protection against unsafe concurrency. The goal is to minimize the amount of time spent in synchronized code and get threads back to parallel execution as quickly as possible.
Although producer/consumer is a good model to keep in mind, there are other ways that reading and writing threads might interact. Consider the following programming problem, similar to one you might find in real life.
As a rising star in a bank’s IT department, you’ve been given the job
of creating a new bank account class called SynchronizedAccount. This
class must have methods to support the following operations: deposit,
withdraw, and check balance. Each method should print a status message
to the screen on completion. Also, the method for withdraw should return
false and do nothing if there are insufficient funds. Because the
latest system is multi-threaded, these methods must be designed so that
the bookkeeping is consistent even if many threads are accessing a
single account. No money should magically appear or disappear.
There’s an additional challenge. To maximize concurrency,
SynchronizedAccount should be synchronized differently for read and
write accesses. Any number of threads should be able to
check the balance on an account simultaneously, but only one thread can
deposit or withdraw at a time.
To solve this problem, our implementation of the class has a balance
variable to record the balance, but it also has a readers variable to
keep track of the number of threads which are reading from the account
at any given time.
public class SynchronizedAccount {
private double balance = 0.0;
private int readers = 0; Next, the getBalance() method is called by threads which wish to read
the balance.
public double getBalance() throws InterruptedException {
double amount;
synchronized(this) { (1)
readers++;
}
amount = balance; (2)
synchronized(this) {
if(--readers == 0) (3)
notifyAll(); (4)
}
return amount;
}| 1 | Access to the readers variable is synchronized. |
| 2 | After passing that first synchronized block, the code which stores the
balance is no longer synchronized. In this way, multiple readers can access
the data at the same time. For this example, the concurrency controls we
have are overkill. The command amount = balance does not take a great
deal of time. If it did, however, it would make sense for readers to
execute it concurrently as we do. |
| 3 | After reading the balance, this method
decrements readers. |
| 4 | If readers reaches 0, a call to notifyAll() is
made, signaling that threads trying to deposit to or withdraw from the
account can continue. |
public void deposit(double amount) throws InterruptedException {
changeBalance(amount);
System.out.println("Deposited $" + amount + ".");
}
public boolean withdraw(double amount)
throws InterruptedException {
boolean success = changeBalance(-amount);
if(success)
System.out.println("Withdrew $" + amount + ".");
else
System.out.println("Failed to withdraw $" +
amount + ": insufficient funds.");
return success;
}The deposit() and withdraw() methods are wrappers for the
changeBalance() method, which has all the interesting concurrency
controls.
protected synchronized boolean changeBalance(double amount) (1)
throws InterruptedException {
boolean success;
while(readers > 0) (2)
wait();
if(success = (balance + amount > 0)) (3)
balance += amount;
return success;
}
}| 1 | The changeBalance() method is synchronized so that it can have
exclusive access to the readers variable. It’s also marked protected
because SynchronizedAccount will be used as a parent class in
Chapter 17. |
| 2 | As long as readers is
greater than 0, this method will wait. |
| 3 | Eventually, the readers should finish their job and notify the waiting writer which can finish changing the balance of the account. |
14.5. Pitfalls: Synchronization challenges
As you can see from the dining philosophers problem, synchronization tools help us get the right answer but also create other difficulties.
14.5.1. Deadlock
Deadlock is the situation when two or more threads are both waiting for the others to complete, forever. Some combination of locks or other synchronization tools has forced a blocking dependence onto a group of threads which will never be resolved.
In the past, people have described four conditions which must exist for deadlock to happen.
-
Mutual Exclusion: Only one thread can access the resource (often a lock) at a time.
-
Hold and Wait: A thread holding a resource can ask for additional resources.
-
No Preemption: A thread holding a resource cannot be forced to release it by another thread.
-
Circular Wait: Two or more threads hold resources which make up a circular chain of dependency.
We illustrate deadlock with an example of how not to solve the dining philosophers problem. What if all the philosophers decided to pick up the chopstick on her left and then the chopstick on her right? If the timing was just right, each philosopher would be holding one chopstick in her left hand and be waiting forever for her neighbor on the right to give up a chopstick. No philosopher would ever be able to eat. Here’s that scenario illustrated in code.
public class DeadlockPhilosopher extends Thread {
public static final int SEATS = 5; (1)
private static boolean[] chopsticks = new boolean[SEATS]; (2)
private int seat;
public DeadlockPhilosopher(int seat) { (3)
this.seat = seat;
}| 1 | We define a constant for the number of seats. |
| 2 | We create a shared boolean array called chopsticks so that all philosophers
can know which chopsticks are in use. |
| 3 | The constructor assigns each philosopher a seat number. |
public static void main(String args[]) {
DeadlockPhilosopher[] philosophers = new DeadlockPhilosopher[SEATS];
for(int i = 0; i < SEATS; i++) {
philosophers[i] = new DeadlockPhilosopher(i);
philosophers[i].start(); (1)
}
try {
for(int i = 0; i < SEATS; i++)
philosophers[i].join(); (2)
}
catch(InterruptedException e) {
e.printStackTrace();
}
System.out.println("All philosophers done.");
}| 1 | In main(), we create and start a thread for each
philosopher. |
| 2 | Then, we wait for them to finish which, sadly, will never happen. |
After setting up the class and the main() method, things get interesting
in the run() method.
public void run() {
try {
getChopstick(seat); (1)
Thread.sleep(50); (2)
getChopstick((seat + 1) % SEATS); (3)
}
catch(InterruptedException e) {
e.printStackTrace();
}
eat();
}| 1 | First a philosopher tries to get her left chopstick. |
| 2 | Then she sleeps for 50 milliseconds. |
| 3 | Finally, she tries to get her right chopstick. We mod by SEATS so that the
last philosopher will try to get the chopstick at the beginning of the array. |
Without sleeping, this code would usually run just fine. Every once in a while, the philosophers would become deadlocked, but it would be hard to predict when. By introducing the sleep, we can all but guarantee that the philosophers will deadlock every time.
The remaining two methods are worth examining to see how the synchronization is done, but by getting the two chopsticks separately above, we’ve already gotten ourselves into trouble.
private void getChopstick(int location) throws InterruptedException {
if(location < 0)
location += SEATS;
synchronized(chopsticks) {
while(chopsticks[location])
chopsticks.wait();
chopsticks[location] = true;
}
System.out.println("Philosopher " + seat +
" picked up chopstick " + location + ".");
}
private void eat() {
// Done eating, put back chopsticks
synchronized(chopsticks) {
chopsticks[seat] = false;
if(seat == 0)
chopsticks[SEATS - 1] = false;
else
chopsticks[seat - 1] = false;
chopsticks.notifyAll();
}
}
} Here’s another example of deadlock. We emphasize deadlock because it’s one of the most common and problematic issues with using synchronization carelessly.
Consider two threads which both need access to two separate resources.
In our example, the two resources are random number generators. The goal
of each of these threads is to acquire locks for the two shared random
number generators, generate two random numbers each, and sum the numbers
generated. (Note that locks are totally unnecessary for this problem
since access to Random objects is synchronized.)
import java.util.Random;
public class DeadlockSum extends Thread {
private static Random random1 = new Random();
private static Random random2 = new Random();
private boolean reverse;
private int sum;The class begins by creating shared static Random objects
random1 and random2. Then, in the main() method, the main thread
spawns two new threads, passing true to one and false to the other.
public static void main(String[] args) {
Thread thread1 = new DeadlockSum(true);
Thread thread2 = new DeadlockSum(false);
thread1.start();
thread2.start();
try {
thread1.join();
thread2.join();
}
catch(InterruptedException e) {
e.printStackTrace();
}
}Next, the mischief begins to unfold. One of the two threads stores
true in its reverse field.
public DeadlockSum(boolean reverse) {
this.reverse = reverse;
}Finally, we have the run() method where all the action happens. If the
two running threads were both to acquire locks for random1 and random2 in
the same order, everything would work out fine. However, the reversed
thread locks on random2 and then random1, with a sleep() in
between. The non-reversed thread tries to lock on random1 and then
random2.
public void run() {
if(reverse) {
synchronized(random2) {
System.out.println("Reversed Thread: locked random2");
try{ Thread.sleep(50); }
catch(InterruptedException e) {
e.printStackTrace();
}
synchronized(random1) {
System.out.println("Reversed Thread: locked random1");
sum = random1.nextInt() + random2.nextInt();
}
}
}
else {
synchronized(random1) {
System.out.println("Normal Thread: locked random1");
try { Thread.sleep(50); }
catch(InterruptedException e) {
e.printStackTrace();
}
synchronized(random2) {
System.out.println("Normal Thread: locked random2");
sum = random1.nextInt() + random2.nextInt();
}
}
}
}
}If you run this code, it should invariably deadlock with thread1
locked on random2 and thread2 locked on random1. No sane
programmer would intentionally code the threads like this. In fact, the
extra work we did to acquire the locks in opposite orders is exactly
what causes the deadlock. For more complicated programs, there may be
many different kinds of threads and many different resources. If two
different threads (perhaps written by different programmers) need
both resource A and resource B at the same time but try to acquire them
in reverse order, this kind of deadlock can occur without such an
obvious cause.
For deadlock of this type, the circular wait condition can be broken by ordering the resources and always locking the resources in ascending order. Of course, this solution only works if there is some universal way of ordering the resources and the ordering is always followed by all threads in the program.
Ignoring the deadlock problems with the example above, it gives a nice example of the way Java intended synchronization to be done: when possible, use the resource you need as its own lock. Many other languages require programmers to create additional locks or semaphores to protect a given resource, but this approach causes problems if the same lock is not consistently used. Using the resource itself as a lock is an elegant solution.
14.5.2. Starvation and livelock
Starvation is another problem which can occur with careless use of synchronization tools. Starvation is a general term which covers any situation in which some thread never gets access to the resources it needs. Deadlock can be viewed as a special case of starvation since none of the threads which are deadlocking makes progress.
The dining philosophers problem was framed around the idea of eating with humorous intent. If a philosopher is never able to acquire chopsticks, that philosopher will quite literally starve.
Starvation doesn’t necessarily mean deadlock, however. Examine the
implementation in Example 14.2 for the bank account.
That solution is correct in the sense that it preserves mutual
exclusion. No combination of balance checks, deposits, or withdrawals
will cause the balance to be incorrect. Money will neither be created
nor destroyed. A closer inspection reveals that the solution is not
entirely fair. If a single thread is checking the balance, no other
thread can make a deposit or a withdrawal. Balance checking threads
could be coming and going constantly, incrementing and decrementing the
readers variable, but if readers never goes down to zero, threads
waiting to make deposits and withdrawals will wait forever.
Another kind of starvation is livelock. In deadlock, two or more threads get stuck and wait forever, doing nothing. Livelock is similar except that the two threads keep executing code and waiting for some condition that never arrives. A classic example of livelock is two polite (but oddly predictable) people speaking with each other: Both happen to start talking at exactly the same moment and then stop to hear what the other has to say. After exactly one second, they both begin again and immediately stop. Lather, rinse, repeat.
Imagine three friends going to a party. Each of them starts getting ready at different times. They follow the pattern of getting ready for a while, waiting for their friends to get ready, and then calling their friends to see if the other two are ready. If all three are ready, then the friends will leave. Unfortunately, if a friend calls and either of the other two aren’t ready, he’ll become frustrated and stop being ready. Perhaps he’ll realize that he’s got time to take a shower or get involved in some other activity for a while. After finishing that activity, he’ll become ready again and wait for his friends to become ready.
If the timing is just right, the three friends will keep becoming ready, waiting for a while, and then becoming frustrated when they realize that their friends aren’t ready. Here’s a rough simulation of this process in code.
public class Livelock extends Thread {
private static int totalReady = 0; (1)
private static Object lock = new Object(); (2)
public static void main(String[] args) { (3)
Livelock friend1 = new Livelock();
Livelock friend2 = new Livelock();
Livelock friend3 = new Livelock();| 1 | First, we create a shared variable called totalReady which
tracks the total number of friends ready. |
| 2 | To avoid race conditions, a shared Object called lock will be used to control
access to totalReady. |
| 3 | Then, the main() method creates Livelock
objects representing each of the friends. |
try {
friend1.start();
Thread.sleep(100);
friend2.start();
Thread.sleep(100);
friend3.start();
friend1.join();
friend2.join();
friend3.join();
}
catch(InterruptedException e) {
e.printStackTrace();
}
System.out.println("All ready!");
}The rest of the main() method starts each of the threads representing
the friends running, with a 100 millisecond delay before the next thread
starts . Then, it waits for them all to finish. If
successful, it’ll print All ready! to the screen.
public void run() {
boolean done = false;
try {
while(!done) { (1)
Thread.sleep(75); // Prepare for party (2)
synchronized(lock) {
totalReady++; (3)
}
Thread.sleep(75); // Wait for friends (4)
synchronized(lock) {
if(totalReady >= 3) (5)
done = true;
else
totalReady--; (6)
}
}
}
catch(InterruptedException e) {
e.printStackTrace();
}
}
}| 1 | In the run() method, each friend goes through a loop until the done
variable is true. |
| 2 | In this loop, an initial call to Thread.sleep()
for 75 milliseconds represents preparing for the party. |
| 3 | After that,
totalReady is incremented by one. |
| 4 | Then, the friend waits for another 75 milliseconds. |
| 5 | Finally, he checks to see if everyone else is ready by
testing whether totalReady is 3. |
| 6 | If not, he decrements totalReady and repeats the process. |
At roughly 75 milliseconds into the simulation, the first friend becomes ready, but he doesn’t check with his friends until 150 milliseconds. Unfortunately, the second friend doesn’t become ready until 175 milliseconds. He then checks with his friends at 225 milliseconds, around which time the first friend is becoming ready a second time. However, the third friend isn’t ready until 275 milliseconds. When he then checks at 350 milliseconds, the first friend isn’t ready anymore. On some systems the timing might drift such that the friends all become ready at the same time, but it could take a long, long while.
In reality, human beings would not put off going to a party indefinitely. Some people would decide that it was too late to go. Others would go alone. Others would go over to their friends' houses and demand to know what was taking so long. Computers are not nearly as sensible and must obey instructions, even if they cause useless repetitive patterns. Realistic examples of livelock are hard to show in a short amount of code, but they do crop up in real systems and can be very difficult to predict.
14.5.3. Sequential execution
When designing a parallel program, you might notice that synchronization tools are necessary to get a correct answer. Then, when you run this parallel version and compare it to the sequential version, it runs no faster or, worse, runs slower than the sequential version. Too much zeal with synchronization tools can produce a program which gives the right answer but doesn’t exploit any parallelism.
For example, we can take the run() method from the parallel
implementation of matrix multiply given in Example 13.11
and use the synchronized keyword to lock on the matrix itself.
public void run() {
synchronized(c) {
for(int i = lower; i < upper; i++)
for(int j = 0; j < c[i].length; j++)
for(int k = 0; k < b.length; k++)
c[i][j] += a[i][k] * b[k][j];
}
}In this case, only a single thread would have access to the matrix at any given time, and all speedup would be lost.
For the parallel version of matrix multiply we gave earlier, no synchronization is needed. In
the case of the producer/consumer problem, synchronization is necessary,
and the only way to manage the buffer properly is to enforce sequential
execution. Sometimes sequential execution can’t be avoided, but you
should always know which pieces of code are truly executing in parallel
and which aren’t if you hope to get the maximum amount of speedup. The
synchronized keyword should be used whenever it’s needed, but no
more.
14.5.4. Priority inversion
In Chapter 13 we suggest that you rarely use thread priorities. Even good reasons to use priorities can be thwarted by priority inversion. In priority inversion, a lower priority thread holds a lock needed by a higher priority thread, potentially for a long time. Because the high priority thread cannot continue, the lower priority thread gets more CPU time, as if it were a high priority thread.
Worse, if there are some medium priority threads in the system, the low priority thread could hold the lock needed by the high priority thread for even longer because those medium priority threads reduce the amount of CPU time the low priority thread has to finish its task.
14.6. Solution: Dining philosophers
Here we give our solution to the dining philosophers problem. Although deadlock was the key pitfall we were trying to avoid, many other issues can crop up in solutions to this problem. A single philosopher might be forced into starvation, or all philosophers might experience livelock through some pattern of picking up and putting down chopsticks which never quite works out. A very simple solution could allow the philosophers to eat, one by one, in order. Then, the philosophers would often and unnecessarily be waiting to eat, and the program would approach sequential execution.
The key element that makes our solution work is that we force a philosopher to pick up two chopsticks atomically. The philosopher will either pick up both chopsticks or neither.
import java.util.Random;
public class DiningPhilosopher extends Thread {
public static final int SEATS = 5;
private static boolean[] chopsticks = new boolean[SEATS];
private int seat;
public DiningPhilosopher(int seat) {
this.seat = seat;
}We begin with a similar setup as the deadlocking version given in Example 14.3.
public static void main(String args[]) {
DiningPhilosopher[] philosophers = new DiningPhilosopher[SEATS];
for(int i = 0; i < SEATS; i++) {
philosophers[i] = new DiningPhilosopher(i);
philosophers[i].start(); (1)
}
try {
for(int i = 0; i < SEATS; i++)
philosophers[i].join(); (2)
}
catch(InterruptedException e) {
e.printStackTrace();
}
System.out.println("All philosophers done.");
}| 1 | In main(), we create and start a thread for each
philosopher. |
| 2 | Then, we wait for them to finish. |
public void run() { (1)
for(int i = 0; i < 100; i++) { (2)
think();
getChopsticks();
eat();
}
}
private void think() { (3)
Random random = new Random();
try {
sleep(random.nextInt(20) + 10);
}
catch(InterruptedException e) {
e.printStackTrace();
}
}| 1 | This run() method is different from the deadlocking version but not in
a way that prevents deadlock. |
| 2 | We added the for loop so that you could
see the philosophers eat and think many different times without
problems. |
| 3 | We also added the think() method to randomize the amount of
time between eating so that each run of the program is less
deterministic. |
private void getChopsticks() { (1)
int location1 = seat;
int location2 = (seat + 1) % SEATS;
synchronized(chopsticks) { (2)
while(chopsticks[location1] || chopsticks[location2]) { (3)
try {
chopsticks.wait(); (4)
}
catch(InterruptedException e) {
e.printStackTrace();
}
}
chopsticks[location1] = true;
chopsticks[location2] = true;
}
System.out.println("Philosopher " + seat + " picked up chopsticks " +
location1 + " and " + location2 + ".");
}| 1 | The real place where deadlock is prevented is in the getChopsticks()
method. As in Example 14.3, we mod by SEATS so that the last philosopher
tries to get the first chopstick in the array. |
| 2 | The philosopher acquires the chopsticks lock. |
| 3 | Then, she picks up the two chopsticks she needs only if both are available. |
| 4 | Otherwise, she waits. |
private void eat() { (1)
// Done eating, put back chopsticks
synchronized(chopsticks) { (2)
chopsticks[seat] = false;
if(seat == 0)
chopsticks[SEATS - 1] = false;
else
chopsticks[seat - 1] = false;
chopsticks.notifyAll(); (3)
}
}
}| 1 | Finally, in the eat() method, the philosopher eats the rice. We would
assume that some other computation would be done here in a realistic
problem before entering the synchronized block. The eating itself
does not require a lock. |
| 2 | After eating’s done, the lock is acquired to give back the chopsticks (hopefully after some cleaning). |
| 3 | Then, all waiting philosophers are notified that some chopsticks may have become available. |
Our solution prevents deadlock and livelock because some philosopher will get control of two chopsticks eventually, yet there are still issues. Note that each philosopher only eats and thinks 100 times. If, instead of philosophers sharing chopsticks, each thread were a server sharing network storage units, the program could run for an unspecified amount of time: days, weeks, even years. If starvation is happening to a particular philosopher in our program, the other philosophers will finish after 100 rounds, and the starved philosopher can catch up. If there were no limitation on the loop, a starving philosopher might never catch up.
Even if we increase the number of iterations of the loop quite a lot,
we probably wouldn’t see starvation of an individual thread because we’re
cheating in another way. Some unlucky sequence of chopstick accesses
by two neighboring philosophers could starve the philosopher between
them. By making the think() method wait a random amount of time, such
a sequence will probably be interrupted. If all philosophers thought for
exactly the same amount of time each turn, an unlucky pattern could
repeat. It’s not unreasonable to believe that the amount
of thinking a philosopher (or a server) will do at any given time will
vary, but the behavior depends on the system.
It’s very difficult to come up with a perfect answer to some synchronization problems. Such problems have been studied for many years, and research continues to find better solutions.
14.7. Exercises
Conceptual Problems
-
What’s the purpose of the
synchronizedkeyword? How does it work? -
The language specification for Java makes it illegal to use the
synchronizedkeyword on constructors. During the creation of an object, it’s possible to leak data to the outside world by adding a reference to the object under construction to some shared data structure. What’s the danger of leaking data in this way? -
If you call
wait()ornotify()on an object, it must be inside of a block synchronized on the same object. If not, the code will compile, but anIllegalMonitorStateExceptionmay be thrown at run time. Why is it necessary to own the lock on an object before callingwait()ornotify()on it? -
Why is it safer to call
notifyAll()thannotify()? If it’s generally safer to callnotifyAll(), are there any scenarios in which there are good reasons to callnotify()? -
Imagine a simulation of a restaurant with many waiter and chef objects. The waiters must submit orders to the kitchen staff, and the chefs must divide the work among themselves. How would you design this system? How would information and food be passed from waiter to chef and chef to waiter? How would you synchronize the process?
-
Let’s reexamine the code that increments a variable with several threads from Section 14.3. We can rewrite the
run()method as follows.public synchronized void run() { for(int i = 0; i < COUNT/THREADS; i++) counter++; }Will this change fix the race condition? Why or why not?
-
Examine our deadlock example from Example 14.4. Explain why this example fulfills all four conditions for deadlock. Be specific about which threads and which resources are needed to show each condition.
-
What’s priority inversion? Why can a low priority thread holding a lock be particularly problematic?
Programming Practice
-
In Example 14.1 the
Bufferclass used to implement a solution to the producer/consumer problem only has a single lock. When the buffer is empty and a producer puts an item in it, both producers and consumers are woken up. A similar situation happens whenever the buffer is full and a consumer removes an item. Re-implement this solution with two locks so that a producer putting an item into an empty buffer only wakes up consumers and a consumer removing an item from a full buffer only wakes up producers. -
In Example 14.2 we used the class
SynchronizedAccountto solve a bank account problem. As we mention in Section 14.5.2, depositing and withdrawing threads can be starved out by a steady supply of balance checking threads. Add additional synchronization tools toSynchronizedAccountso that balance checking threads will take turns with depositing and withdrawing threads. If there are no depositing or withdrawing threads, make your implementation continue to allow an unlimited number of balance checking threads to read concurrently. -
The solution to the dining philosophers problem given in Section 14.6 suffers from the problem that a philosopher could be starved by the two philosophers on either side of her, if she happened to get unlucky. Add variables to each philosopher which indicate hunger and the last time a philosopher has eaten. If a given philosopher is hungry and hasn’t eaten for longer than her neighbor, her neighbor shouldn’t pick up the chopstick they share. Add synchronization tools to enforce this principle of fairness. Note that your solution must not cause deadlock. Although one philosopher may be waiting on another who is waiting on another and so on, some philosopher in the circle must have gone hungry the longest, breaking circular wait.
Experiments
-
Critical sections can slow down your program by preventing parallel computation. However, the locks used to enforce critical sections can add extra delays on top of that. Design a simple experiment which repeatedly acquires a lock and does some simple operation. Test the running time with and without the lock. See if you can estimate the time needed to acquire a lock in Java on your system.
-
Design a program which experimentally determines how much time a thread is scheduled to spend running on a CPU before switching to the next thread. To do this, first create a tight loop which runs a large number of iterations, perhaps 1,000,000 or more. Determine how much time it takes to run a single run of those iterations. Then, write an outer loop which runs the tight loop several times. Each iteration of the outer loop, test to see how much time has passed. When you encounter a large jump in time, typically at least 10 times the amount of time the tight loop usually takes to run to completion, record that time. If you run these loops in multiple threads and average the unusually long times together for each thread, you should be able to find out about how long each thread waits between runs. Using this information, you can estimate how much time each thread is allotted. Bear in mind that your this average is only an estimation. Some JVMs will change the amount of CPU time allotted to threads for various reasons. If you’re on a multicore machine, it will be more difficult to interpret your data since some threads will be running concurrently.
-
Create an experiment to investigate priority inversion in the following way.
-
Create two threads, setting the priority of the first to
MIN_PRIORITYand the priority of the second toMAX_PRIORITY. Start the first thread running but wait 100 milliseconds before starting the second thread. The first thread should acquire a shared lock and then perform some lengthy process such as finding the sum of the sines of the first million integers. After it finishes its computation, it should release the lock, and print a message. The second thread should try to acquire the lock, print a message, and then release the lock. Time the process. Because the lock is held by the lower priority thread, the higher priority thread will have to wait until the other thread is done for it to finish. -
Once you have a feel for the time it takes for these two threads to finish alone, create 10 more threads that must also perform a lot of computation. However, do not make these threads try to acquire the lock. How much do they delay completion of the task? How does this delay relate to the number of cores in your processor? How much does the delay change if you set the priorities of these new threads to
MAX_PRIORITYorMIN_PRIORITY?
-
15. Constructing Graphical User Interfaces
A good sketch is better than a long speech.
15.1. Problem: Math tutor
Most people are used to using interacting with programs through a GUI rather than a command-line interface. In this chapter, our problem is to write a GUI program that can allow young math students to practice their arithmetic. Specifically, we’re interested in addition, subtraction, multiplication, and division with small, positive integers. For this program, we’ll consider addition and subtraction basic and multiplication and division advanced. Our program should allow the user to select a check box in a menu setting the mode to advanced or basic.
The user should then be able to select one of the four operations from another menu. Once the operation is selected, the program should generate a random problem testing that operation. The problem should be displayed as a label on the program with a text field to one side. The user should be able to enter an answer in the text field and hit a button to submit it. The program should check the answer and display the updated number of correct and incorrect answers.

MathTutor. (a) No menu selected. (b) Type selected. (c) Operations selected. (d) Attempting to answer an addition problem.Figure 15.1 shows the final program in four different states. The window on the top left appears when the program is first initialized, with the “Submit” button disabled until a problem is generated. The top right and the bottom left show each of the two menus open. The bottom right shows the program when an addition problem has been generated and the user is about to answer.
15.2. Concepts: Graphical user interfaces
The program shown above with its menus, labels, buttons, and other interactive components is called a graphical user interface or GUI. A GUI is a means of communication between a computer program and a (usually human) user. Although it’s possible for some programs such as scripts to interact with a GUI, most program-to-program communication is done in other ways.
While communication through input and output on the command line is one way to communicate with a program, GUIs offer a user-friendly alternative that has become extremely commonplace. In fact, GUIs are so common that many people have never used anything else to interact with programs and may not even suspect that other kinds of interaction are possible.
This chapter will teach you how to write programs with GUIs. Although GUIs can make input and output easier for the user, the programmer has to shoulder the burden of arranging the layout and appearance of the GUI and making it function properly. Chapter 7 introduced a way to make simple GUIs, but those GUIs came in preset flavors designed for displaying a message, getting a range of responses in the form of buttons or lists, or reading a short piece of text as input. In this chapter we’ll explore ways to make GUIs of arbitrary complexity with no limitations on the size or shape of the GUI or the components it contains.
A typical GUI consists of a frame (also known as a window) on which are displayed one or more components (known as widgets), such as panels, buttons, and text boxes. Panels are used to organize the contents within the frame. A frame contains at least one panel, but additional ones can be added. Each panel can also contain components: buttons, labels, text boxes, and even other panels. Using code to create a GUI with all the components laid out exactly where you want them is half the work of making a GUI-driven program in Java.
Some components like labels are read-only to the user. They display information such as status messages. Other components allow the user to give input to the program. Reading GUI input is usually done in response to an event. Handling events inside of a program is the other half of writing a GUI program in Java. Layout is concerned with appearance, but event handling is concerned with functionality.
Some IDEs such as IntelliJ have graphical tools that automatically generate GUI layout code for you. It’s fast to create a GUI with such tools, but the GUIs they create are often inflexible and look terrible when the window is resized. We focus on how to write all the code yourself because doing so gives you more control and helps you understand Java GUIs better.
15.2.1. Swing and AWT
Most of the components you’ll use to create GUIs are defined in
classes that belong to the Java Swing library. This library contains
many interfaces and classes. In earlier chapters, you have seen and
used one class from the Swing library, the JOptionPane class.
Some components of the Swing library are
built on another library known as the Abstract Window Toolkit or AWT.
The AWT is an older library which provides direct access to OS
components. Thus, an AWT Button object in Microsoft Windows creates a
Windows button. Swing, however, draws its own button. AWT GUIs look
exactly like other GUIs from the same OS. Swing GUIs can be configured
to look similar using look and feel settings, or developers can choose
to use a default Java look and feel that will look similar across all platforms.
We’ll discuss many Swing components such as JButton and JTextField. Swing
components usually have a J at the beginning of their names to
distinguish them from similar AWT components. (The AWT contains Button
and TextField. If you see examples from other sources using components
that don’t start with J, they’re probably using AWT.) Although Swing
is built on top of the older AWT library, it’s not a good idea to mix
Swing and AWT components in a single GUI.
The Swing library is far too large for us to cover in its entirety. Instead, our goal is to show you how to construct GUIs using some of the most common Java components. Once you’ve grasped the material in this chapter, you’ll be able to read and understand how to use many other interesting Swing components, as well as other Java libraries for constructing GUIs. The JavaFX library is a newer library that was intended to replace Swing, but it hasn’t been widely adopted. Although it’s still available, JavaFX is no longer included with Java 11 and higher and must be downloaded as a separate library.
15.3. Syntax: GUIs in Java
15.3.1. Creating a frame
A frame is the Java terminology for a window. GUI components in Java will
usually be found on a frame. In Swing, a frame is an object whose type is
derived from the JFrame class. Here’s a line of code that creates a JFrame object.
JFrame frame = new JFrame("Empty Frame");The above statement declares and creates a JFrame object named
frame. The title of the frame is “Empty Frame” and is given as
an argument to the JFrame constructor. Although calling the
constructor creates the frame, you need to make it visible for it to
show up on the screen.
frame.setVisible(true);The setVisible() method causes the frame frame to be visible on
the screen as a window. You can specify its size as follows.
frame.setSize(350,200);The setSize() method sets the width and height of the frame in pixels.
In the above example, the width of frame is set to 350
pixels and its height to 200 pixels. If you don’t set the size (or use a
method like pack() to make a JFrame resize itself to the appropriate
size for its contents), it might be so tiny that you at first don’t see it.
The window created by the above code is resizable. If you don’t want the user to be able to resize the window, you can specify that as well.
frame.setResizable(false);Your entire GUI will often be a frame you create and the components inside that frame. You might want your application to end when you close the frame by clicking on the close button toward the top. The actual location of this button depends on the operating system and the look and feel managers you’re using. Regardless, the following statement can be used to set the behavior of the application when you close the frame window.
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);|
Pitfall: Closing frames
Some books and online tutorials suggest setting Using By using It’s still necessary to select some default closing operation. By
default, the operation is set to |
Program 15.1 creates and displays an empty frame with the title “Empty Frame,” much like the code above.
import javax.swing.*; (1)
public class EmptyFrame {
public static void main(String[] args){
JFrame frame = new JFrame("Empty Frame"); (2)
frame.setSize(350,200); (3)
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE); (4)
frame.setVisible(true); (5)
}
}| 1 | This import statement lets the compiler know we’re using the Swing library. |
| 2 | The first statement inside the main() method declares and creates a JFrame object
and assigns a title to it. |
| 3 | Then, we set its size. |
| 4 | Next, we set the default close operation. |
| 5 | Finally, we make the frame visible. |
The frame so created is shown in Figure 15.2.
You may resize the frame at any point in the program even after the frame has been created and made visible. The initial size may or may not be set prior to making the frame visible. Similarly, the frame title can be set and reset at any point in the program.
A single frame might need to open other subsidiary windows from time to time
to ask a question or display some information. To create windows dependent
on a parent frame, use JDialog instead of JFrame. A dialog window made
with JDialog can either be modal (meaning that the user must close it before they
can interact with the parent frame) or non-modal (allowing the user
to interact with it and its parent frame at the same time).
15.3.2. Components
A component (or widget) is an element of a GUI. Java provides a large variety of components including panels, buttons, text boxes, check boxes, radio buttons, and menus. When laying out a GUI, one or more of the components are created and then placed on a frame. A component is declared and created like any other object.
Widget w = new Widget(arguments);Here we use class Widget to represent any Swing component class like
JButton or JTextField. Arguments supplied while constructing a
component allow you to set attributes such as its icon, color, size, or
text to display. Most of these attributes can be changed after creation.
Although components can be added directly to a frame, it’s often convenient to lay out a GUI by adding panels to a frame and adding components to those panels. Each panel can hold zero or more components. A panel is also referred to as a container object. Next, we show you how to create a panel, populate it with components, add it to a frame, and display the completed frame.
In Swing, a panel is an instance of the JPanel class and can be created as
follows.
JPanel panel = new JPanel();This statement creates a panel named panel. Thus far, the panel
is empty. We can create two buttons and add them to panel.
JButton thisButton = new JButton("This");
JButton thatButton = new JButton("That");
panel.add(thisButton);
panel.add(thatButton);Here, we create two buttons named thisButton and thatButton.
It’s common for component variables to reflect what kind of component
they are by appending a description, in this case Button, to their names.
These buttons are labeled "This" and
"That", but their labels could be any String values. Then, we add
the two buttons to the panel.
frame.add(panel);This statement adds the panel to an existing frame called frame.
Another useful component is JTextField. It creates a text field that can
be used by a program for both input and output of String data.
JTextField field = new JTextField("This is not a pipe.");This statement creates a JTextField component named field.
When displayed, it’ll show the text “This is not a pipe.”
The user can change this text by typing, but we won’t know when the text
has been change without the event handling tools discussed in
Section 15.3.3. The following example combines several
of the components we’ve introduced into one program.
We can write an application with a GUI that contains three buttons labeled “This,” “That,” and “Exit.” In addition, it contains a text field that initially displays the text, “Text input and output area”
In this example the buttons are only for display. You can click each one, but the program won’t do anything. The text field won’t be changed by the program after it’s initialized either. In the next subsection we’ll add actions to each button and make the program more useful.
import javax.swing.*;
public class FrameWithPanel {
public static void main(String[] args){
JFrame frame = new JFrame("Button Example"); (1)
JPanel panel = new JPanel(); (2)
JButton thisButton = new JButton("This"); (3)
JButton thatButton = new JButton("That");
JButton exitButton = new JButton("Exit");
JTextField field = new JTextField("Text input and output area");
panel.add(thisButton); (4)
panel.add(thatButton);
panel.add(field);
panel.add(exitButton);
frame.add(panel); (5)
frame.setSize(350,200);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true); (6)
}
}| 1 | We first create a frame named frame. |
| 2 | Then, we make a panel named panel. |
| 3 | Next, we create three buttons named thisButton, thatButton, and exitButton and a text field named field. |
| 4 | We add the buttons and the text field to panel. |
| 5 | We add panel to frame. |
| 6 | After setting the size and the closing operation, the frame is made visible. |
The final GUI is shown in Figure 15.3. The sequence in which you add the buttons to the panel determines the appearance of the GUI. That’s why the text field appears before the “Exit” button. Note that the same GUI may look different on different platforms.
In addition to JTextField, JTextArea and JPasswordField are two other
components useful for entering text. The JTextArea component is designed
for larger passages of text and allows multiple lines. The JPasswordField
component functions the same as a JTextField except that each character
of input text is displayed as a meaningless echo character designed to hide
sensitive information like a password.
Figure 15.4(a) shows a GUI with a JTextArea, and
Figure 15.4(b) shows a GUI with a JPasswordField.

15.3.3. Adding actions to components
We can design a GUI so that when a user clicks a button, the program responds by printing a message to the terminal, changing a text field, playing a sound, or any other action that a Java program can perform. Clicking a button generates an event. In Swing, an event is processed by one or more listeners. Java provides various types of listeners, some of which are introduced here. Next, we show you how to write listeners to handle events generated by a few different kinds of components.
The ActionListener interface
Java provides an ActionListener interface. This interface has a single
method named actionPerformed(). This method takes an ActionEvent as
input and performs a suitable action based on the event. A JButton
object generates ActionEvent when it’s pressed. Any class that
implements the ActionListener interface can be registered as an action
listener on a JButton or any other component that generates an
ActionEvent.
As discussed in Chapter 10, an interface is a set of
method signatures. If a class implements an interface, it promises that its objects will
have all of the methods in that interface. If a class implements
ActionListener, it’s saying that it knows what to do when an action is
performed. The following statements show how to add an ActionListener
to a button and implement its actionPerformed() method.
JButton thisButton = new JButton("This");
thisButton.addActionListener(new ActionListener() {
public void actionPerformed(ActionEvent e) {
// Code to perform an action goes here
}
});The first line above creates a button named thisButton. The remaining code
adds an action listener to the button. The process of adding an action
listener to an object is also known as registering a listener on the
object. Note that the sole argument to this addActionListener() method
is a newly created ActionListener object. Inside this newly created
and anonymous ActionListener object, we implement the
actionPerformed() method. Whatever code we want to execute in response
to the clicking of the thisButton button goes inside the
actionPerformed() method.
This syntax may look strange to you. ActionListener is an interface,
which can’t be instantiated. What’s that new keyword doing? It’s
doing something pretty amazing by creating an instance of an anonymous
class. On the fly, we’re creating a class that has never existed
before. It doesn’t even have a name! All we know about it is that it
implements the interface ActionListener.
Note that there are braces after the constructor call, defining what’s
inside of this class. Inside, we have only created an
actionPerformed() method, but we could have created fields as well as
other methods. It’s a little ugly to create a whole new class and
instantiate it in the middle of calling the addActionListener()
method, but it’s also very convenient. We need to supply an object that
reacts to the event exactly the way we want it to. Since one doesn’t
exist yet, we have to create it. Of course, it’s possible to supply any
object that implements the ActionListener interface, not just
instances of anonymous classes. For more information about nested
classes, inner classes, and anonymous classes, refer to
Section 9.4 and Section 10.4.
Now we can modify Program 15.2 to respond to button
clicks. When the thisButton button is clicked, the program will display the
message “You can get with this.” in the text field. Similarly, when the
thatButton button is clicked, the program will display “Or you can get with that.”
import javax.swing.*;
import java.awt.event.*;
public class FrameWithPanelAndActions {
public static void main(String[] args){
JFrame frame = new JFrame("Button Example");
JPanel panel = new JPanel();
JButton thisButton = new JButton("This");
JButton thatButton = new JButton("That");
JButton exitButton = new JButton("Exit");
JTextField field = new JTextField("Text input and output area");
panel.add(thisButton);
panel.add(thatButton);
panel.add(field);
panel.add(exitButton);
// Add action listeners to various buttons
thisButton.addActionListener(new ActionListener() {
public void actionPerformed(ActionEvent e){
field.setText("You can get with this.");
}
});
thatButton.addActionListener(new ActionListener(){
public void actionPerformed(ActionEvent e){
field.setText("Or you can get with that.");
}
});
exitButton.addActionListener(new ActionListener(){
public void actionPerformed(ActionEvent e){
System.out.println("Exit");
frame.dispose();
}
});
frame.add(panel);
frame.setSize(350,200);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true);
}
}Program 15.3 is largely the same as
Program 15.2. It adds the same buttons and text
field but then adds an action listener to each button. The action
performed when the thisButton and thatButton buttons are clicked is to display
a message in the text box. When the exitButton button is clicked, the
listener displays a message on the terminal and exits the program.
The action listeners can be added either before or after the panel has been set up but should be added before the frame is made visible.
In the previous example, we added an ActionListener object to each
button and implemented its actionPerformed() method with anonymous
inner classes. An alternate way to use ActionListener is to implement
ActionListener on the surrounding class and include an
actionPerformed() method exactly once instead of creating several
individual anonymous inner classes which each handle an event. Let’s
examine one such implementation in
Program 15.4 and contrast it with
Program 15.3. Note that both programs
generate the same GUI and exhibit identical behavior.
ActionListener at the class level.import javax.swing.*;
import java.awt.event.*;
public class AlternateActionListener implements ActionListener {
private JFrame frame = new JFrame("Button Example");
private JPanel panel = new JPanel();
private JButton thisButton = new JButton("This");
private JButton thatButton = new JButton("That");
private JButton exitButton = new JButton("Exit");
private JTextField field = new JTextField("Text input and output area");
public AlternateActionListener (){ (1)
thisButton.addActionListener(this);
thatButton.addActionListener(this);
exitButton.addActionListener(this);
panel.add(thisButton);
panel.add(thatButton);
panel.add(field);
panel.add(exitButton);
frame.add(panel);
frame.setSize(350,200);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true);
}
public void actionPerformed(ActionEvent e){ (2)
Object button = e.getSource(); (3)
if(button == thisButton) (4)
field.setText("You can get with this.");
else if(button == thatButton)
field.setText("Or you can get with that.");
else {
System.out.println("Exit");
frame.dispose();
}
}
public static void main(String[] args){ (5)
new AlternateActionListener();
}
}| 1 | The constructor adds an ActionListener to each button. The listener added is this, specifying that the AlternateActionListener object is the one that will process any action event generated by the buttons. The remainder of the code for the constructor is essentially the same as that from the main() method in Program 15.3. |
| 2 | A class that implements ActionListener must include an actionPerformed() method. It has exactly one parameter, an ActionEvent object. Whenever an action event occurs, its attributes are bundled into an ActionEvent object and passed into the actionPerformed() method. |
| 3 | The getSource() method returns a reference to the object that generated the event. Variable button holds the object returned by
getSource(). |
| 4 | These if statements compare button with thisButton and thatButton to determine if either of these generated the event. Then, a suitable message is displayed in the field text field. If neither button generated the event, it must have been exitButton, so the frame disposes itself after displaying “Exit” on the terminal. |
| 5 | The main() method creates an instance of AlternateActionListener and finishes. The program doesn’t end there because the threads of the GUI are already running. |
There are a few differences between
Program 15.3 and
Program 15.4. In
the second program, most of the code has been
moved from the main() method to the constructor. Various objects,
namely the frame, the panel, all three
buttons, and the text box are now fields of the object instead of local
variables in the main() method. The buttons need to be fields so that the
actionPerformed() method can compare against them, and the text box needs
to be a field so that the method can change it.
We’ve examined two styles of adding an ActionListener to a Java
program. The choice of style depends on your needs. Adding
an anonymous ActionListener to each component makes it easy to specify an
action for each one, but the syntax is ugly. Using a named class (often the main program class or a
subclass of JFrame) as the ActionListener allows you to handle many
events in a centralized location. It can be easier to find errors when
all events are handled in one actionPerformed() method, but the method
can become complex since it needs to determine which component generated the event.
The ItemListener interface
An ItemListener can be attached to a component such as a check box or a
radio button to listen for when it’s selected or deselected. When you select
a check box, a ✓ sign appears to its left, and an ItemEvent is
generated. When you select an already checked check box, the sign
disappears, and another ItemEvent is generated.
Creating a check box is very much like creating a button, except
that we use the JCheckBox component instead of JButton.
When it’s initially created, a check box is unchecked.
JCheckBox checkBox = new JCheckBox("Check the oven");Just as the ActionListener interface only has a single method, the
ItemListener interface only has one as well, itemStateChanged(), which
takes a single parameter of type ItemEvent.
An ActionEvent and an ItemEvent are similar, but one reason that Java
has two different interfaces with two different kinds of events is
because an ItemEvent has more information: By using the
getStateChange() method, it’s possible to tell whether the component
that fired the ItemEvent is now selected or deselected.
checkBox.addItemListener(new ItemListener(){
public void itemStateChanged(ItemEvent e) {
if(e.getStateChange() == ItemEvent.SELECTED)
checkBox.setText("We checked the oven!");
else
checkBox.setText("No one checked the oven!");
}
});Below is an example of a GUI with three check boxes.
The following program shows a GUI with three check boxes labeled “Nasty”, “Brutish”, and “Short”. When each is clicked, it’ll update a text field saying that your life either is or isn’t nasty, brutish, or short, depending on whether or not the clicked check box is currently selected.
import javax.swing.*;
import java.awt.event.*;
public class CheckBoxExample {
public static void main(String[] args){
JFrame frame = new JFrame("Check Box Example"); (1)
JPanel panel = new JPanel();
JCheckBox nastyCheckBox = new JCheckBox("Nasty"); (2)
JCheckBox brutishCheckBox = new JCheckBox("Brutish");
JCheckBox shortCheckBox = new JCheckBox("Short");
JTextField field = new JTextField("Here's what your life is like.");
panel.add(nastyCheckBox); (3)
panel.add(brutishCheckBox);
panel.add(shortCheckBox);
panel.add(field);
// Add item listeners to the check boxes
nastyCheckBox.addItemListener(new ItemListener() { (4)
public void itemStateChanged(ItemEvent e) {
if(e.getStateChange() == ItemEvent.SELECTED)
field.setText("Your life is nasty.");
else
field.setText("Your life isn't nasty.");
}
});
brutishCheckBox.addItemListener(new ItemListener(){
public void itemStateChanged(ItemEvent e) {
if(e.getStateChange() == ItemEvent.SELECTED)
field.setText("Your life is brutish.");
else
field.setText("Your life isn't brutish.");
}
});
shortCheckBox.addItemListener(new ItemListener(){
public void itemStateChanged(ItemEvent e) {
if(e.getStateChange() == ItemEvent.SELECTED)
field.setText("Your life is short.");
else
field.setText("Your life isn't short.");
}
});
frame.add(panel); (5)
frame.setSize(350,200);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true);
}
}| 1 | Just as in previous examples, we create a frame and a panel. |
| 2 | We make three check boxes and a text field. |
| 3 | Then we add all four components to the panel. |
| 4 | We create an ItemListener for each check box
to update the text field with an appropriate message
based on whether the check box is now checked or unchecked. Note that
the most recent message will overwrite whatever text was previously
in the text field. |
| 5 | Like previous examples, we add the panel to the frame, set the size, set the default close operation, and show the frame. |
Figure 15.5 shows this GUI after the “Brutish” check box has been clicked.
All JCheckBox objects could have an ActionListener added to them
as well. We could change the listener for the nastyCheckBox above to the following,
and it would function the same. To do so, we must ask the nastyCheckBox if it’s
currently selected by calling its isSelected() method.
nastyCheckBox.addActionListener(new ActionListener() {
public void actionPerformed(ActionEvent e) {
if(nastyCheckBox.isSelected())
field.setText("Your life is nasty.");
else
field.setText("Your life isn't nasty.");
}
});Another Swing component that can be used with an ItemListener is JRadioButton.
Radio buttons are similar to check boxes in that clicking one will select it.
However, radio buttons are almost always used in a group. When one radio button
in the group is selected, all others are deselected, guaranteeing that only one
radio button can be selected at a time.
For example, the following code will create three radio buttons, only one of which can be selected.
JRadioButton smarterButton = new JRadioButton("Smarter than the average bear");
JRadioButton lessSmartButton = new JRadioButton("Less smart than the average bear");
JRadioButton asSmartButton = new JRadioButton("As smart as the average bear");
ButtonGroup group = new ButtonGroup();
group.add(smarterButton);
group.add(lessSmartButton);
group.add(asSmartButton);The ButtonGroup object provides the logical grouping that guarantees a maximum
of one JRadioButton will be selected. This grouping is only for the purposes of
selection, and the radio buttons still need to be added to a panel or a frame or some other
GUI container to display them.
With check boxes, an ItemListener didn’t provide much of an advantage over an
ActionListener. A radio button, however, can be deselected not by clicking on it
but by clicking on another radio button. Thus, using an ItemListener allows us
to handle the event when a radio button is deselected, even though it wasn’t clicked
itself, as illustrated in the following example.
The program below shows a GUI with three radio buttons labeled “Half empty”, “Half full”, and “Twice the needed size”, describing a partially filled glass of water from the perspective of an optimist, a pessimist, or an engineer, respectively. When each radio button is selected, it’ll update the first text field describing the glass from the given perspective. However, when a radio button is deselected by clicking another one, it’ll update the second text field to describe what the glass isn’t, now that we’re in a different perspective.
import javax.swing.*;
import java.awt.event.*;
public class RadioButtonExample {
public static void main(String[] args){
JFrame frame = new JFrame("Radio Button Example");
JPanel panel = new JPanel();
JRadioButton halfEmptyButton = new JRadioButton("Half empty"); (1)
JRadioButton halfFullButton = new JRadioButton("Half full");
JRadioButton twiceTheSizeButton = new JRadioButton("Twice the needed size");
JTextField positiveField = new JTextField("Positive statement about the glass.");
JTextField negativeField = new JTextField("Negative statement about the glass.");
ButtonGroup group = new ButtonGroup(); (2)
group.add(halfEmptyButton);
group.add(halfFullButton);
group.add(twiceTheSizeButton);
panel.add(halfEmptyButton); (3)
panel.add(halfFullButton);
panel.add(twiceTheSizeButton);
panel.add(positiveField);
panel.add(negativeField);
// Add item listeners to the radio buttons
halfEmptyButton.addItemListener(new ItemListener() { (4)
public void itemStateChanged(ItemEvent e) {
if(e.getStateChange() == ItemEvent.SELECTED)
positiveField.setText("The glass is half empty.");
else
negativeField.setText("And it's not half empty.");
}
});
halfFullButton.addItemListener(new ItemListener(){
public void itemStateChanged(ItemEvent e) {
if(e.getStateChange() == ItemEvent.SELECTED)
positiveField.setText("The glass is half full.");
else
negativeField.setText("And it's not half full.");
}
});
twiceTheSizeButton.addItemListener(new ItemListener(){
public void itemStateChanged(ItemEvent e) {
if(e.getStateChange() == ItemEvent.SELECTED)
positiveField.setText("The glass is twice the needed size.");
else
negativeField.setText("And it's not twice the needed size.");
}
});
frame.add(panel); (5)
frame.setSize(350,200);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true);
}
}| 1 | We make three radio buttons and two text fields. |
| 2 | We add the three radio buttons to a group. |
| 3 | Then we add the five components to the panel. |
| 4 | We create an ItemListener for each radio button. When the event
is a selection, it will update the first text field with a message
that matches the radio button. When the event is a deselection,
it will update the second text field with a message that suggests
the opposite of the radio button. |
| 5 | Like previous examples, we add the panel to the frame, set the size, set the default close operation, and show the frame. |
Figure 15.6(a) shows this GUI before any radio buttons have been selected. Figure 15.6(b) shows this GUI after the “Half full” radio button’s been selected. Figure 15.6(c) shows this GUI after the “Twice the needed size” radio button’s been selected. In this final step, note that the second text field reads “And it’s not half full.” because the “Half full” button was just deselected.

The MouseListener interface
Clicking a button or a check box is useful, but a mouse can generate events
in other ways too. For example, in a screen full of pictures, you might want to
highlight a picture when the cursor hovers over it. Or you might want to
create a drawing program which uses a mouse as a pen. To process general
mouse events, we need an object that implements the MouseListener
interface, which defines the following methods.
-
mouseClicked() -
mouseEntered() -
mouseExited() -
mousePressed() -
mouseReleased()
The function of each method is implied by its name. The mouseEntered()
event fires when the mouse cursor moves into the area above a component.
Conversely, the mouseExited() event fires when a mouse cursor was over
a component and has just moved away. The mousePressed() event fires
when a mouse button is pressed over a component. The mouseReleased()
event fires when a mouse button is released over a component.
The mouseClicked() event is a combination of
both the mousePressed() and mouseReleased() events, occurring only
if a mouse button was pressed and then released while the cursor was
over a component. As you can see, a component only fires events when the
cursor is over it (or has just left). Thus, a component only
reports events that have to do with it, not the general state of the
mouse.
Each method in MouseListener receives a MouseEvent object as its
argument. To handle mouse events, a class must implement the
MouseListener interface. Doing so is similar to the implementation of the
ActionListener interface from the previous section, but implementing
MouseListener requires a definition for each of the five methods
listed above. The next example illustrates MouseListener in use.
We can write a program that displays a GUI containing two buttons labeled “One” and “Two.” A text box will display a suitable message when the cursor enters a button. When a button is clicked, the text box should display the total number of times that button has been clicked.
MouseListener interface.import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
public class SimpleMouseEvents implements MouseListener { (1)
private JFrame frame = new JFrame("Mouse Events");
private JTextField status = new JTextField("Mouse status comes here.");
private JButton oneButton = new JButton("One");
private JButton twoButton = new JButton("Two");
private int oneClicks = 0, twoClicks = 0; // Number of clicks
public SimpleMouseEvents() { (2)
JPanel panel = new JPanel();
oneButton.addMouseListener(this);
twoButton.addMouseListener(this);
panel.add(oneButton);
panel.add(twoButton);
panel.add(status);
frame.add(panel);
frame.setSize(275,200);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true);
}
// Implement all abstract methods in MouseListener
public void mouseEntered(MouseEvent e) { (3)
if (e.getSource() == oneButton)
status.setText("Mouse enters One.");
else
status.setText("Mouse enters Two.");
}
public void mouseClicked(MouseEvent e) { (4)
if (e.getSource() == oneButton) {
oneClicks++;
status.setText("One clicked "+ oneClicks + " times.");
}
else {
twoClicks++;
status.setText("Two clicked "+ twoClicks + " times.");
}
}
public void mouseExited(MouseEvent e) {} // Unused methods (5)
public void mousePressed(MouseEvent e) {}
public void mouseReleased(MouseEvent e) {}
public static void main(String[] args){ (6)
new SimpleMouseEvents();
}
}| 1 | We declare class SimpleMouseEvents, implementing the MouseListener interface. The following few lines declare frame frame, buttons one and two, and a text box status. Two integers oneClicks and twoClicks are initialized to 0 and are used to keep track of the number of times each button has been clicked. |
| 2 | The first line of the SimpleMouseEvents constructor creates the panel
panel. It doesn’t need to be a field, and it’s always preferable to
keep a variable local if it can be. The next two lines add a MouseListener to the two buttons. Note the use of this in the argument to addMouseListener() which refers to the object being created by the constructor. Next, the panel is set up and added to the frame. Finally the frame size and its default close operations are set, and the frame is made visible. |
| 3 | The mouseEntered() method is invoked when the cursor enters either of the two buttons. First, we retrieve the source of the event using the getSource() method and identify which object generated the event. A suitable message is displayed in the status box using the setText() method. |
| 4 | The mouseClicked() method is invoked when the mouse cursor is clicked above a button. As before, we retrieve the source of the event using the getSource() method. A suitable message, including the number of clicks, is displayed in the text box. Of course, recording button clicks could have been done with an ActionListener instead. |
| 5 | MouseListener methods that aren’t used must be implemented, but their bodies can be left empty. |
| 6 | The only job of the main() method is to create an instance of
SimpleMouseEvents. |
Program 15.5 generates the GUI shown in Figure 15.7.
Mouse adapter
Creating a MouseListener requires all five methods in the interface to
be implemented. In many cases, as in Example 15.7,
there’s no need to implement all the methods because we’re not
interested in all the corresponding events. In such situations we’re
forced to include empty methods.
However, you might want to include the methods only when they’re
needed. The MouseAdapter class helps us avoid implementing
methods we don’t need.
MouseAdapter is an abstract class, unlike the MouseListener
interface. The advantage of using MouseAdapter is that it already
provides a skeletal implementation of each method needed to process
mouse events. We can override these implementations as needed, and we
don’t need to provide an implementation of a method that’s not used.
Program 15.6 is a revised version of Program 15.5. Remember that an abstract class is extended whereas an interface is implemented.
MouseAdapter abstract class.import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
public class SimpleMouseAdapter extends MouseAdapter { (1)
private JFrame frame = new JFrame("Mouse Events");
private JTextField status = new JTextField("Mouse status comes here.");
private JButton oneButton = new JButton("One");
private JButton twoButton = new JButton("Two");
private int oneClicks = 0, twoClicks = 0;
public SimpleMouseAdapter () {
JPanel panel = new JPanel();
oneButton.addMouseListener(this);
twoButton.addMouseListener(this);
panel.add(oneButton);
panel.add(twoButton);
panel.add(status);
frame.add(panel);
frame.setSize(275,200);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true);
}
// Override only those methods we want
public void mouseEntered(MouseEvent e) { (2)
if (e.getSource() == oneButton)
status.setText("Mouse enters One.");
else
status.setText("Mouse enters Two.");
}
public void mouseClicked(MouseEvent e) { (3)
if (e.getSource() == oneButton) {
oneClicks++;
status.setText("One clicked "+ oneClicks + " times.");
}
else {
twoClicks++;
status.setText("Two clicked "+ twoClicks + " times.");
}
}
public static void main(String[] args){
new SimpleMouseAdapter ();
}
}| 1 | Class SimpleMouseAdapter extends the abstract class MouseAdapter. Thus, it inherits all the empty methods defined in MouseAdapter. |
| 2 | We override the method mouseEntered(). |
| 3 | We override the method mouseClicked(). No other methods need to be overridden in this example. |
Other event listeners
In this chapter we describe three types of listeners in Java,
ActionListener, ItemListener and MouseListener. You may have noticed that none of
the mouse events we discussed involved the movement of the mouse inside
of the component, only whether it was entering or exiting the component.
Because tracking mouse movement is more computationally expensive than
tracking simple presses, releases, enters, and exits, Java uses yet another
listener to handle mouse movement, MouseMotionListener. It contains
the methods mouseDragged() and mouseMoved(), which are used to
handle mouse movement with or without the button pressed.
Java provides several other listeners to handle a variety of events. For
example, the DocumentListener can be attached to a JTextField or a
JTextArea object to listen to document events, which include the
insertUpdate() event that’s fired when a character is inserted the
text box. A KeyListener can also be attached to text boxes to listen
to key events such as the return key being typed, which can have similar
functionality. These events could be useful when developing a text editor
application, for example.
After you’ve mastered the contents of this chapter, you may plan to write more complex GUIs than the ones we discuss. For further information, you might want to follow the Java tutorial on writing event listeners at the Oracle Swing Events tutorial site.
15.3.4. Adding sounds and images
Sounds and images can also be added to a Java GUI application. While
Java offers a rich set of sound APIs, we restrict our examples to
playing sound clips from audio files that come in au or wav formats.
We also introduce the ImageIcon class to create icons from image
files.
Sounds
There are many ways to play sounds in Java, but the simplest is through the Clip interface. Let’s see how we can create an appropriate Clip
object.
Clip clip = AudioSystem.getClip();This statement creates a new Clip object using a static method from
the AudioSystem class in the javax.sound.sampled package. To use
clip, we need an audio file to play.
File soundFile = new File("sounds/trumpet.wav"); (1)
clip.open(AudioSystem.getAudioInputStream(soundFile)); (2)| 1 | Here we create a File object corresponding to the location of an audio
file we want to play. In this case, we’re trying to play a file called
trumpet.wav in a sounds directory that’s in the same directory as
our program. The location of the file could be much more complicated
or even entered by the user. |
| 2 | Then, we use the AudioSystem class to make an audio stream from the
file and open it with clip. Note that the two methods on this line can
throw a number of exceptions, depending on whether the file is in a usable
format and your computer’s audio system is ready. |
clip.start();This command will play the clip in clip loaded from the specified
file, exactly once. If you want to play the clip in a loop, use the
loop() method. You can specify a specific number of times to loop
or use the Clip.LOOP_CONTINUOUSLY constant to make it loop an unlimited
number of times.
clip.loop(Clip.LOOP_CONTINUOUSLY);To stop a clip from playing, use the stop() method.
clip.stop();Now that we’ve seen how to create, open, play, and stop an audio clip, we’re ready to write a program that can play sounds.
We can write a program to play a loop of a bird chirping or a dog barking when the corresponding button is clicked. Our program only has two sounds, but more could be added.

We can include a button labeled “Stop Sound” that stops the playback of sounds when clicked. When it starts, the GUI will look like Figure 15.8(a). Note that the “Stop Sound” button is gray, showing that it’s disabled. The complete program is shown below.
import java.io.*; (1)
import java.awt.event.*;
import javax.swing.*;
import javax.sound.sampled.*;
public class AnimalSounds {
public static void main (String[] args) throws Exception {
JFrame frame = new JFrame("Animal Sounds");
JPanel panel = new JPanel();
JButton chirpButton = new JButton("Chirp");
JButton barkButton = new JButton("Bark");
JButton stopButton = new JButton("Stop Sound");
JTextField field = new JTextField("Click Chirp or Bark.");
File chirpFile = new File("sounds/chirp.wav"); (2)
File barkFile = new File("sounds/bark.wav");
Clip chirpClip = AudioSystem.getClip(); (3)
chirpClip.open(AudioSystem.getAudioInputStream(chirpFile));
Clip barkClip = AudioSystem.getClip();
barkClip.open(AudioSystem.getAudioInputStream(barkFile));
panel.add(chirpButton);
panel.add(barkButton);
panel.add(stopButton);
panel.add(field);
frame.add(panel);
stopButton.setEnabled(false); (4)| 1 | Many import statements are needed to cover all the library classes and interfaces used to play sounds. |
| 2 | After creating a number of GUI elements, we define the files for the two sounds. |
| 3 | Then, we create chirpClip and barkClip and open audio streams
corresponding to their sound files. |
| 4 | Note that we start with the stop button disabled. |
chirpButton.addActionListener(new ActionListener() { (1)
public void actionPerformed(ActionEvent e){
field.setText("Playing chirp.");
barkButton.setEnabled(false);
chirpClip.loop(Clip.LOOP_CONTINUOUSLY);
stopButton.setEnabled(true);
}
});
barkButton.addActionListener(new ActionListener(){ (2)
public void actionPerformed(ActionEvent e){
field.setText("Playing bark.");
chirpButton.setEnabled(false);
barkClip.loop(Clip.LOOP_CONTINUOUSLY);
stopButton.setEnabled(true);
}
});
stopButton.addActionListener(new ActionListener(){ (3)
public void actionPerformed(ActionEvent e){
field.setText("Click Chirp or Bark.");
chirpClip.stop();
barkClip.stop();
barkButton.setEnabled(true);
chirpButton.setEnabled(true);
stopButton.setEnabled(false);
}
});
frame.setSize(275,200); // Set size in pixels
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true); // Display it
}
}| 1 | Here we define the action listener for chirpButton, which
disables barkButton, tells the user that the chirp sound is playing, plays
the sound, and enables the stop button. |
| 2 | The action listener for barkButton button is similar. |
| 3 | The action listener for stopButton doesn’t know which sound is playing,
so it stops both sounds and then disables the stopButton. |
When chirpButton is clicked, the GUI looks like Figure 15.8(b).
Images and icons
Images are often useful when creating GUIs. In this section we show you
how to use images to create icons and then use those icons to decorate
buttons and labels. First, let’s see how an icon object can be created.
Suppose we have a picture file named smile.jpg in a directory named
pictures. Note that the pictures directory should be located in same
directory as the class files for your program. The following statement
creates an object of type ImageIcon from this picture.
ImageIcon smileIcon = new ImageIcon("pictures/smile.jpg");The file name, along with its path, is passed to the
ImageIcon constructor as a string. Now we can add the image to a
button.
JButton smile = new JButton();
smile.add(smileIcon);Similarly, you can add an image to a label. The next example gives a simple program that creates a button with an image.
Figure 15.9 shows a GUI with a button decorated with a
picture. Program 15.8 gives the code to create this
GUI using the ImageIcon class.
import javax.swing.*;
import java.awt.*;
public class IconExample {
public static void main(String[] args) {
JFrame frame = new JFrame("Icon Example");
ImageIcon smileIcon = new ImageIcon("pictures/smile.jpg"); (1)
JButton smileButton = new JButton(smileIcon); (2)
frame.add(smileButton);
frame.setSize(325,250);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true);
}
}| 1 | An image icon is created from a JPEG file named smile.jpg located in
the pictures directory. |
| 2 | We create a button named smileButton and decorate it with an icon
by supplying it as an argument to the JButton constructor. If
the file can’t be found, the program will fail quietly. This means that
no exception is thrown. Instead, the button will appear without an image. |
Labels, icons, and text
In some applications you might want to show a picture with an attached
text label. For example, a shopping cart application for an online clothing
store might shows pictures of clothes, each labeled with a name
and a price. The JLabel class is flexible, able to display text alone,
an image alone, or both. However, a JLabel is designed for displaying
information and can’t read user input.
Here are three different ways to create a label.
ImageIcon hibiscus = new ImageIcon("pictures/hibiscus.jpg")
JLabel textOnly = new JLabel("Text only");
JLabel flower = new JLabel(hibiscus);
JLabel labeledflower = new JLabel("Red Hibiscus", hibiscus, JLabel.CENTER);The first JLabel constructor above creates a label displaying only
text, namely, “Text only.” The second constructor creates a label
decorated with an icon created from a picture. The third constructor
creates a label with the same icon and additional text. The last
argument in this third case is JLabel.CENTER, a constant that
specifies that the content of the label (both the image and the text)
should be placed horizontally in the center of the label. A horizontal
alignment of left or right could also be specified using the constants
JLabel.LEFT or JLabel.RIGHT, respectively.
Sometimes you might want to place the text below the icon that decorates the label. To do so, you could set the horizontal and vertical positions of the text as follows.
flower.setVerticalTextPosition(JLabel.BOTTOM);
flower.setHorizontalTextPosition(JLabel.CENTER);Figure 15.10(a) is generated by Program 15.9.

import javax.swing.*;
import java.awt.*;
public class LabelExample {
public static void main(String[] args) {
JFrame frame = new JFrame("Label Example");
ImageIcon hibiscusIcon = new ImageIcon("pictures/hibiscus.jpg");
JLabel flower = new JLabel("Red Hibiscus", hibiscusIcon, JLabel.CENTER);
flower.setVerticalTextPosition(JLabel.BOTTOM); (1)
flower.setHorizontalTextPosition(JLabel.CENTER); (2)
frame.add(flower);
frame.setSize(300,250);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true);
}
}| 1 | Vertically position the text on the bottom of the label. |
| 2 | Horizontally center the text on the label. |
You will see the GUI shown in Figure 15.10(b) if the alignment instructions on these two lines are omitted.
15.3.5. Layout managers
Java provides a number of layout managers to assist with the design of
GUIs. A layout manager controls the placement of
components on a frame or panel. Every container has a default layout
manager, but it’s possible to change that manager to a different one.
In this section we’ll introduce the three layout managers FlowLayout,
GridLayout, and BorderLayout. Java also provides several other layout
managers, each designed for different situations.
FlowLayout
The FlowLayout manager is one of simplest. When a
container is using the FlowLayout manager, components will be added in
order from left to right. When there’s no more space, subsequent
components will be added starting on the next row. In addition, each row of
components is centered within the container. The JPanel container uses
FlowLayout by default, but it’s possible to set it explicitly as
well.
JPanel panel = new JPanel(new FlowLayout());When we’ve added more than one component to a JFrame in previous
examples, we’ve first added them to a JPanel. The reason we did so is
because FlowLayout is the default layout manager for
JPanel containers. Although every JFrame has a container, it uses
the BorderLayout manager by default, which would have complicated our
earlier examples. The next example illustrates FlowLayout further.
FlowLayoutProgram 15.10 creates a GUI with several buttons.
FlowLayout.import javax.swing.*;
import java.awt.*;
public class FlowLayoutExample {
public static void main(String[] args) {
JFrame frame = new JFrame("FlowLayout Example"); (1)
JPanel panel = new JPanel(new FlowLayout()); (2)
final int MAX_BUTTONS = 6;
for(int i = 0; i < MAX_BUTTONS; i++) (3)
panel.add(new JButton(" " + i + " "));
frame.add(panel);
frame.setSize(300,200);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setResizable(false);
frame.setVisible(true);
}
}| 1 | We first create a frame. |
| 2 | We create a panel and set its layout manager to FlowLayout. |
| 3 | This for loop is used to create new buttons, label them appropriately, and add them to the panel. |
The FlowLayout manager places the buttons along a number of rows depending on the width of the frame.
If the container changes size, the components will react by "'flowing'" into different rows, hence the name.
The GUI created is shown in Figure 15.11.
FlowLayout manager to generate a GUI containing six buttons.GridLayout
The GridLayout manager lays out components in a grid with a set number
of rows and columns. As with other layout managers, GridLayout can be
applied to frames and panels.
JFrame frame = new JFrame("Grid Layout Example");
frame.setLayout(new GridLayout(3, 2, 5, 5));This snippet creates a frame named frame and sets its layout manager
to GridLayout. The first two arguments to GridLayout give the number
of rows and columns, respectively. The last two arguments (which are optional)
give the horizontal and vertical gaps between the neighboring cells in the
grid. In this example the frame will contain a total of six cells organized
into three rows with two columns.
Figure 15.12 shows how frame will look after six
buttons, labeled 0 through 5, have been added to it in order. The buttons
were created in the same way as the buttons in Program 15.10, but
they look different because of the GridLayout manager. A key
feature of using GridLayout is that all cells in the grid will be
the same size and will stretch to fill the entire container. Also note
the equal spacing between the neighboring cells. It’s possible to add
more cells or fewer cells than specified in the GridLayout constructor, but
the layout manager will be forced to guess at your intentions.
We can write a program to display pictures of animals and identify which animal the mouse is current hovering over. The animal’s name will be displayed in the title of the frame. Figure 15.13 shows this GUI.
Program 15.11 creates the GUI shown in Figure 15.13.
GridLayout manager.import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
public class AnimalIdentifier extends MouseAdapter { (1)
private JLabel bison, dove, gecko, spider; (2)
private JFrame frame = new JFrame("Animal Identifier");
public AnimalIdentifier() {
JPanel panel = new JPanel(new GridLayout(2,2,5,5)); (3)
ImageIcon bisonIcon = new ImageIcon("pictures/bison.jpg");
ImageIcon doveIcon = new ImageIcon("pictures/dove.jpg");
ImageIcon geckoIcon = new ImageIcon("pictures/gecko.jpg");
ImageIcon spiderIcon = new ImageIcon("pictures/spider.jpg");
bison = new JLabel(bisonIcon); (4)
bison.addMouseListener(this);
dove = new JLabel(doveIcon);
dove.addMouseListener(this);
gecko = new JLabel(geckoIcon);
gecko.addMouseListener(this);
spider = new JLabel(spiderIcon);
spider.addMouseListener(this);
panel.add(bison); (5)
panel.add(dove);
panel.add(gecko);
panel.add(spider);
frame.add(panel);
frame.setSize(400,400); (6)
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true);
}| 1 | Class AnimalIdentifier extends MouseAdapter so that it can
be added as a MouseListener without the need to implement all of its methods. |
| 2 | We declare four labels and a frame as fields. The labels are named bison, dove, gecko, and spider. |
| 3 | Inside the constructor, we create a panel with a 2 × 2 GridLayout. Then, we create four image icons, one to decorate each label. |
| 4 | Each of the four labels is created with its respective icon. We also add the AnimalIdentifier object we’re constructing as a MouseListener for each label. |
| 5 | The buttons are added to the panel, and the panel is added to the frame. |
| 6 | The last few lines set the size of the frame, set its close operation, and make it visible. |
public void mouseEntered(MouseEvent e) { (1)
Object label = e.getSource(); (2)
if(label == bison)
frame.setTitle("Animal Identifier: Bison");
else if(label == dove)
frame.setTitle("Animal Identifier: Dove");
else if (label == gecko)
frame.setTitle("Animal Identifier: Gecko");
else if (label == spider)
frame.setTitle("Animal Identifier: Spider");
}
public static void main(String[] args) { (3)
new AnimalIdentifier();
}
}| 1 | Since AnimalIdentifier extends MouseListener, we only need to implement the single MouseListener method we care about, mouseEntered(). |
| 2 | We get the label the mouse entered. We compare this label to the four labels and change the frame title correspondingly. |
| 3 | The main() method creates a new instance of
class AnimalIdentifier, launching the GUI. |
Play with Program 15.11. What happens when you resize the window?
BorderLayout
The BorderLayout manager is the default one for a JFrame. It allows
components to be laid out spatially in regions of a container. These
regions are north, south, east, west, and center. This layout is
intuitively easy to understand, but it’s difficult to describe
precisely.
You can only add one component to each region of the layout, and adding a component to any region is optional. The regions will stretch or shrink to accommodate the components inside. The north and south regions will only be as tall as needed to hold their contents, but their width will stretch as wide as the entire container. The east and west regions will only be as wide as needed to hold their contents, but their height will stretch as tall as needed to fit the remaining height of the container. Both the height and the width of the center region will stretch as big as it needs to fill the container.
BorderLayoutHere’s an example of a frame using BorderLayout. Five buttons have
been added, one to each region, using the program shown below. Since the default layout manager of a JFrame is a BorderLayout,
we don’t need to state it explicitly, although we do in this case.
BorderLayout.import javax.swing.*;
import java.awt.*;
public class BorderLayoutExample {
public static void main(String[] args) {
JFrame frame = new JFrame("BorderLayout Example");
frame.setLayout(new BorderLayout());
frame.add(new JButton("North"), BorderLayout.NORTH);
frame.add(new JButton("South"), BorderLayout.SOUTH);
frame.add(new JButton("East"), BorderLayout.EAST);
frame.add(new JButton("West"), BorderLayout.WEST);
frame.add(new JButton("Center"), BorderLayout.CENTER);
frame.setSize(400,250);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true);
}
}
BorderLayout generated by Program 15.12.Unlike FlowLayout or GridLayout, the location must be specified to
add a component to a BorderLayout. To do so, the add() method
takes a second parameter, which is one of the constants BorderLayout.NORTH,
BorderLayout.SOUTH, BorderLayout.EAST, BorderLayout.WEST, or
BorderLayout.CENTER, depending on where you want to add the component.
If you don’t specify a second parameter, the component will be added to
the center region. Since only one component can be in each region,
adding a component to a region that’s already occupied will replace the
old component with the new one.
At first glance, BorderLayout seems that it would rarely be useful.
However, this layout is frequently used because it establishes a spatial
relationship between different parts of a GUI. A
container with a BorderLayout generally has other containers with
their own layouts added to its regions, as shown in the following
example.
We can make a GUI application that functions as a simple calculator. The calculator has the ten digits 0-9, a plus button, a minus button, and an enter button. At the top is a display that shows the current value.
We create ten JButton objects for the digits and three more JButton
objects for plus, minus, and enter. The display is a JLabel. The code
is given below.
import javax.swing.*;
import java.awt.*;
public class CalculatorLayout {
public static void main(String[] args) {
JFrame frame = new JFrame("Calculator Layout");
frame.setLayout(new BorderLayout());
JPanel numbers = new JPanel(new GridLayout(4,3));
numbers.add(new JButton("7"));
numbers.add(new JButton("8"));
numbers.add(new JButton("9"));
numbers.add(new JButton("4"));
numbers.add(new JButton("5"));
numbers.add(new JButton("6"));
numbers.add(new JButton("1"));
numbers.add(new JButton("2"));
numbers.add(new JButton("3"));
numbers.add(new JButton("0"));
numbers.add(new JButton("+"));
numbers.add(new JButton("-"));
frame.add(numbers, BorderLayout.CENTER);
JButton enter = new JButton("Enter");
frame.add(enter, BorderLayout.SOUTH);
JLabel display = new JLabel("0");
frame.add(display, BorderLayout.NORTH);
frame.setSize(300,350);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true);
}
}
This program uses a frame with a BorderLayout to arrange components around
a central panel with a GridLayout. First, we
put the ten digit buttons in a panel with a GridLayout having 4 rows
and 3 columns. We put the plus button and the minus button in the
remaining two cells of the grid. We add this grid panel to the center region
of the frame. We put the enter button in the south region
and the display in the north region.
Note that this program only creates the layout of a simple calculator, not the functionality.
There’s no limit to how deeply you can nest containers within each
other. Sometimes you must use many BorderLayout managers to achieve the
appearance you want. The value of establishing these spatial relationships
is that they’re still valid even when the GUI is resized. Even so, it’s
challenging to make a usable GUI that looks attractive no matter how
the user resizes it or what the resolution of the user’s screen is.
Although there’s not enough space here to discuss strategies for
developing attractive GUIs, it’s worth noting the value of the
setPreferredSize() method that all components have. This method is
one of the best ways to suggest a size for particular components,
especially if other components and containers are going to stretch
as needed. When key components have their sizes set using
setPreferredSize(), the entire frame can be packed using the
pack() method, which sizes the frame to fit its components.
The three layout managers discussed in this section are the simplest,
but there are others. The BoxLayout manager is a useful tool for
laying out components in a line, whether horizontal like a row or
vertical like a column. The GridBagLayout
manager can be used to create complex layouts in a single container
using a grid-based framework that’s much more flexible than
GridLayout, but the complexity of programming GridBagLayout is
significant. The SpringLayout and GroupLayout managers are also
powerful, but they’re designed for use with a GUI builder utility.
15.3.6. Menus
Menus provide a useful form of interface that’s expected from most GUI applications. In this section we show how to create menus and respond to the selection of menu items. Menus are placed on a menu bar. Each menu usually consists of several menu items that could be selected by the user. In addition to simple text, a menu item can be a button, a radio button, check box, or an icon. A menu can have one or more sub-menus opening out of a menu item.
Creating menus
To use menus we have to create a menu bar.
JMenuBar menuBar = new JMenuBar();This statement creates an object of type JMenuBar named menuBar which
can hold menus. A JFrame has only one menu bar. We can create several
menus and add them to the menu bar.
JMenu frenchMenu = new JMenu("French Menu");
JMenu germanMenu = new JMenu("German Menu");
menuBar.add(frenchMenu);
menuBar.add(germanMenu);These statements create two menus named frenchMenu and germanMenu labeled
“French Menu” and “German Menu,” respectively. The two menus can be added to the existing menu bar using the add() method. Menus can be populated
with menu items as follows.
JMenuItem coqAuVin = new JMenuItem("Coq au vin");
JMenuItem moulesFrites = new JMenuItem("Moules-frites");
frenchMenu.add(coqAuVin);
frenchMenu.add(moulesFrites);These statements create two menu items named coqAuVin and
moulesFrites. These menu items are then added to the menu frenchMenu.
After having created a menu bar together with its menus and their
respective menu items, we need a frame so that we can set its menu bar
to the one we created.
JFrame frame = new JFrame("Menu Example");
frame.setJMenuBar(menuBar);These statements create a frame and set its menu bar to menuBar. It’s
possible to use the add() method instead of the setJMenuBar() method
to add a JMenuBar to a JFrame. However, doing so will add the
JMenuBar to the regular content area, not to the menu area.
Figure 15.16 shows a GUI with the menus and menu items added above.
Sometimes you might need to disable a menu item and enable it only under certain conditions.
JMenuItem unusable = new JMenuItem("Currently unusable");
unusable.setEnabled(false);These statements create a menu item named unusable and disable it.
A disabled menu item shows as a gray item and doesn’t respond to
attempts to select it. As we showed in Example 15.9, JButton
objects, like many other components, can be disabled in the same way.
Adding events to menus
An action listener can be added to each menu item, just like a
JButton. Then, when a menu item is clicked by the user, an action
event is generated. A JCheckBoxMenuItem object can be added to a
JMenu as well. This object will have a check box which can be selected
or unselected. A regular JMenuItem object generates an ActionEvent
which is handled by an ActionListener. Like a JCheckBox, a
JCheckBoxMenuItem can also generate an ItemEvent handled by an
ItemListener. Here are examples of both situations.
JMenuItem clickHere = new JMenuItem("Click here");
JCheckBoxMenuItem checkBox = new JCheckBoxMenuItem("Check yourself");
clickHere.addActionListener(this);
checkBox.addItemListener(this);A JMenuItem works just like a JButton. In fact, the same action
listener code could handle events for both buttons and menu items.
Similar to JCheckBox objects, a JCheckBoxMenuItem can be handled with an ActionListener if you only want to know when it’s clicked on. However, you can add an ItemListener if you want to write an event handler that runs whenever the state of its check box changes.
15.4. Solution: Math tutor
Here we give the code to generate the GUI shown in Figure 15.1 which displays basic (addition and subtraction) as well as advanced (multiplication and division) problems.
As shown in Figure 15.1, this GUI has a menu bar consisting of two menus labeled “Type” and “Operations.” The “Type” menu contains a check box labeled “Advanced” while the “Operations” menu contains four menu items labeled “Add,” “Subtract,” “Multiply,” and “Divide.” Note that the “Multiply” and “Divide” menu items start disabled. They’ll be enabled when the user selects the “Advanced” check box.
Before we introduce the program that creates this GUI, we need a helper
class called ProblemGenerator that can randomly generate arithmetic
problems. The class is designed so that the answers are always positive
integers.
import java.util.Random;
import javax.swing.*;
public class ProblemGenerator {
private Random random = new Random();
public int addPractice(JLabel label) {
int a = random.nextInt(12) + 1;
int b = random.nextInt(12) + 1;
label.setText(a + " + " + b + " = ");
return a + b;
}
public int subtractPractice(JLabel label) {
int a = random.nextInt(12) + 1;
int b = a + random.nextInt(12) + 1;
label.setText(b + " - " + a + " = ");
return b - a;
}
public int multiplyPractice(JLabel label) {
int a = random.nextInt(12) + 1;
int b = random.nextInt(12) + 1;
label.setText(a + " \u00D7 " + b + " = ");
return a * b;
}
public int dividePractice(JLabel label) {
int a = random.nextInt(12) + 1;
int b = a*(random.nextInt(12) + 1);
label.setText(b + " \u00F7 " + a + " = ");
return b / a;
}
}The code listed above has methods addPractice(),
subtractPractice(), multiplyPractice(), and dividePractice(). Each
method generates an appropriate math problem, sets an input JLabel to
display the problem, and returns the solution. Note that \u00D7 and
\u00F7 are the Unicode values for the multiplication (×) and division (÷)
symbols.
Program 15.15 generates the GUI in Figure 15.1.
import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
public class MathTutor implements ActionListener, ItemListener {
private JMenuItem add = new JMenuItem("Addition"); (1)
private JMenuItem subtract = new JMenuItem("Subtraction");
private JMenuItem multiply = new JMenuItem("Multiply");
private JMenuItem divide = new JMenuItem ("Divide");
private JLabel score = new JLabel("Score: 0 Correct 0 Incorrect");
private JLabel label = new JLabel();
private JTextField field = new JTextField(10);
private JButton submitButton = new JButton("Submit");
private ProblemGenerator generator = new ProblemGenerator(); (2)
private int correct = 0; (3)
private int incorrect = 0;
private int answer = -1;| 1 | We begin by creating the GUI components that need to interact with event handlers: four menu items, a label, a text field, and a button. |
| 2 | We also create a ProblemGenerator object to help create new problems. |
| 3 | Next, we add int fields to store the number of correct and incorrect answers as well as the answer to the current problem. |
public MathTutor() { (1)
JFrame frame = new JFrame("Math Tutor");
JMenuBar menuBar = new JMenuBar();
JMenu typeMenu = new JMenu("Type");
JMenu operationsMenu = new JMenu("Operations");
JCheckBoxMenuItem advanced = new JCheckBoxMenuItem("Advanced");
// Add listeners to menu items (2)
add.addActionListener(this);
subtract.addActionListener(this);
multiply.addActionListener(this);
divide.addActionListener(this);
advanced.addItemListener(this); (3)
//Add anonymous ActionListener to submitButton (4)
submitButton.addActionListener(new ActionListener() {
public void actionPerformed(ActionEvent e) {
int response = Integer.parseInt(field.getText());
if(response == answer)
correct++;
else
incorrect++;
label.setText("");
score.setText("Score: " + correct + " Correct " +
incorrect + " Incorrect");
submitButton.setEnabled(false);
}
}); | 1 | Inside the MathTutor constructor, we create the frame and the remaining components. |
| 2 | Action listeners are added to the four operations menu items. |
| 3 | An item listener is added to the “Advanced” check box menu item because it requires a different kind of event handler. Note that MathTutor implements both the ActionListener and ItemListener interfaces, allowing it to handle both kinds of events. |
| 4 | Next, we add an anonymous ActionListener just for the submit button. It
reads the response from the text field, converts it into an integer, and checks against the answer. If the response is correct, it increments the counter for correct answers. Otherwise, it increments the counter for incorrect answers. Finally, it updates the score label and disables the submit
button until another operation is chosen from the menu. |
typeMenu.add(advanced); (1)
operationsMenu.add(add); (2)
operationsMenu.add(subtract);
operationsMenu.add(multiply);
operationsMenu.add(divide);
multiply.setEnabled(false); (3)
divide.setEnabled(false);
menuBar.add(typeMenu); (4)
menuBar.add(operationsMenu);
frame.setJMenuBar(menuBar);
// Add components to frame and display GUI (5)
frame.add(score, BorderLayout.NORTH);
frame.add(label, BorderLayout.WEST);
frame.add(field, BorderLayout.EAST);
frame.add(submitButton, BorderLayout.SOUTH);
submitButton.setEnabled(false);
frame.setSize(300, 150);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setVisible(true);
}| 1 | We add the advanced menu item to the type menu. |
| 2 | Then, we add the four kinds of operations to the operations menu. |
| 3 | The multiply and divide menu items are disabled because the application starts in basic mode. |
| 4 | The menus are then added to the menu bar, and the menu bar is set on the frame. |
| 5 | Finally, the labels and text field are added to the frame, which is made visible. Note that these components can be added directly to the frame with the parameters BorderLayout.NORTH, BorderLayout.EAST, and BorderLayout.WEST because JFrame objects use the BorderLayout manager by default. |
public void itemStateChanged(ItemEvent e) {
if(e.getStateChange() == ItemEvent.SELECTED) {
add.setEnabled(false);
subtract.setEnabled(false);
multiply.setEnabled(true);
divide.setEnabled(true);
}
else {
add.setEnabled(true);
subtract.setEnabled(true);
multiply.setEnabled(false);
divide.setEnabled(false);
}
}The itemStateChanged() method enables the multiply and divide menus and
disables the add and subtract menus if the advanced check box is
selected and does the reverse if it’s been unselected.
public void actionPerformed(ActionEvent e){
Object menuItem = e.getSource();
if(menuItem == add)
answer = generator.addPractice(label);
else if(menuItem == subtract)
answer = generator.subtractPractice(label);
else if(menuItem == multiply)
answer = generator.multiplyPractice(label);
else if(menuItem == divide)
answer = generator.dividePractice(label);
submitButton.setEnabled(true);
field.setText("");
}Depending on which menu item fired the event, the actionPerformed() method calls the
appropriate method from the ProblemGenerator object to create and then
display a math problem on label. The correct answer is stored in answer.
Note that this actionPerformed() method doesn’t handle the submit button
because it has its own anonymous class handler. We use both styles of listener
to keep the code simpler: Handling the submit button separately makes sense
because it’s different, but handling the operations menu items together makes
sense because they’re similar.
public static void main(String[] args){
new MathTutor();
}
}Last but not least, the main() method creates an instance of MathTutor, initiating GUI construction and display.
15.5. Concurrency: GUIs
Stand-alone Java programs have at least one thread, the main thread. Applications with GUIs create additional threads to manage the GUI behind the scenes.
Although a GUI will create several threads, the most relevant of these
is the event dispatch thread (EDT). This thread handles events like
button clicks. When you write actionPerformed() methods, remember
that the EDT is the one that will actually execute the code inside.
If you’re writing a complex program, the EDT may interact with many other threads, and the synchronization issues discussed in Chapter 14 will become important. However, only the EDT is allowed to change the state of components in a GUI. Using other threads to do so will work some of the time, but it’s not thread-safe and violates the design of Swing.
15.5.1. Worker threads
Thread safety is not the most common multi-threaded GUI problem, however. Unresponsive GUIs can be found on almost every platform, as you’ve no doubt experienced. In Java, unresponsive GUIs usually happen when the programmer uses the event dispatch thread to perform some task that takes too long. Because the EDT is responsible for updating the GUI, the GUI freezes, and the user has to wait.
This problem presents quite a conundrum. On the one hand, the EDT is the only thread allowed to update components. On the other, it has to do its work quickly so that the GUI is responsive. The solution is to spawn worker threads to do the job. When they’re done, they can tell the EDT to update the GUI.
Let’s look at a GUI with two JButton components and two JLabel components.
When one button’s pressed, the EDT goes to sleep for 5 seconds before
displaying an answer on the first label (in this case, approximately
the square root of 2). When the other button’s pressed, it increments
a counter and displays the value in the second label.
import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
public class UnresponsiveGUI implements ActionListener {
private JLabel answerLabel = new JLabel("Answer:");
private JButton computeButton = new JButton("Compute");
private JLabel countLabel = new JLabel("0");
private JButton incrementButton = new JButton("Increment");
private int count = 0;
public UnresponsiveGUI() {
JFrame frame = new JFrame("Unresponsive GUI");
frame.setLayout(new GridLayout(4,1));
computeButton.addActionListener(this);
incrementButton.addActionListener(this);
frame.add(answerLabel);
frame.add(computeButton);
frame.add(countLabel);
frame.add(incrementButton);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setSize(300,150);
frame.setVisible(true);
}
public void actionPerformed(ActionEvent e) {
if(e.getSource() == computeButton) {
answerLabel.setText("Computing...");
try {
Thread.sleep(5000);
}
catch(InterruptedException ignore) { }
answerLabel.setText("Answer: " + Math.sqrt(2.0));
}
else {
count++;
countLabel.setText("" + count);
}
}
public static void main(String args[]) {
new UnresponsiveGUI();
}
}
If you click the “Compute” button, the GUI becomes unresponsive. Specifically, nothing will happen when you click the “Increment” button, but you should still be able to move the frame around the desktop on most systems. Furthermore, some thread in the GUI is registering the clicks you do on the “Increment” button, though events triggered by those clicks aren’t handled until after the EDT wakes up. At that point, the counter will shoot up in value unpredictably.
One solution is to create an anonymous inner class that extends
SwingWorker. The SwingWorker class is abstract, but it’s also
generic, meaning that it has type parameters (given in angle brackets)
which specify what type of objects it interacts with. Generic classes
are often containers like LinkedList where the type parameter says
what kind of objects will be kept in the list.
Chapter 18 covers generics
in some depth. The reason we need generics for SwingWorker is so that it
can specify what kinds of answers it produces.
The first type parameter specifies the type that the worker will return when
it completes its work. The second specifies the type that the worker will return
periodically in the process of doing work (which can be useful for
updating progress bars). Examine the following program which has added a
SwingWorker to its actionPerformed() method but is otherwise the
same as Program 15.16.
SwingWorker to avoid becoming unresponsive.import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
public class WorkerGUI implements ActionListener {
private JLabel answerLabel = new JLabel("Answer:");
private JButton computeButton = new JButton("Compute");
private JLabel countLabel = new JLabel("0");
private JButton incrementButton = new JButton("Increment");
private int count = 0;
public WorkerGUI() {
JFrame frame = new JFrame("Worker GUI");
frame.setLayout(new GridLayout(4,1));
computeButton.addActionListener(this);
incrementButton.addActionListener(this);
frame.add(answerLabel);
frame.add(computeButton);
frame.add(countLabel);
frame.add(incrementButton);
frame.setDefaultCloseOperation(JFrame.DISPOSE_ON_CLOSE);
frame.setSize(300,150);
frame.setVisible(true);
}
public void actionPerformed(ActionEvent e) {
if(e.getSource() == computeButton) {
SwingWorker worker = new SwingWorker<String, Void>() { (1)
public String doInBackground() { (2)
try {
Thread.sleep(5000);
}
catch(Exception ignore) {}
return "Answer: " + Math.sqrt(2.0); (3)
}
public void done() { (4)
try {
answerLabel.setText(get());
}
catch (Exception ignore) {}
}
};
worker.execute(); (5)
answerLabel.setText("Computing...");
}
else {
count++;
countLabel.setText("" + count);
}
}
public static void main(String args[]) {
new WorkerGUI();
}
}| 1 | In this program, the first type parameter for the SwingWorker is
String because we’re going to set the text in a JLabel with its
result. The second parameter is Void, meaning that we don’t intend to
return any values periodically. Most child classes of SwingWorker
should override the doInBackground() and done() methods. |
| 2 | The doInBackground() method performs the time-consuming work we
want done on another thread. In our example, the “work” is just going to
sleep, but it will generally be some CPU or I/O intensive process. |
| 3 | Afterward, it returns the answer it found. |
| 4 | The done() method is
called automatically by the EDT after doInBackground() finishes. Note that
the get() method automatically returns whatever answer was produced by
the doInBackground() method. |
| 5 | Once the SwingWorker object has been created, the execute() method starts
it running. |
This GUI will look identical to the unresponsive version (except for the title), but it will remain responsive.
This syntax is not particularly elegant, but it accomplishes a complex
task. It spawns a thread transparently and then notifies the EDT when the
thread has its answer ready. Using a SwingWorker isn’t
always required, but it’s a useful tool to have in your arsenal if you
plan on writing industrial-strength, responsive GUIs.
15.6. Summary
This chapter covers the fundamentals of constructing a GUI to allow users to interact with an application. We show how to add components such as buttons and text boxes and use layout managers to organize their appearance. We show how you can add action listeners and other event handlers so that user interactions like button clicks can trigger useful tasks.
While Java offers a large variety of components and listeners, this introduction is limited to a few of the most commonly used. Once you understand the basics of GUI construction as described in this chapter, it should be easy to understand the extensive Java tutorial at the Oracle Swing Components tutorial site or other reference sources.
15.7. Exercises
Conceptual Problems
-
Both
ActionListenerandMouseListenerinterfaces can be used to process button clicks. Under which circumstances isActionListenerbetter? Under which isMouseListenerbetter? -
What do you expect will happen if you used
setJMenuBar()to set two different menu bars on a singleJFrameobject? -
Describe the situations that the following event listeners are useful for:
ActionListener,MouseListener, andItemListener.
Programming Practice
-
Write a program that creates a GUI containing two buttons labeled “Start” and “Done.” The GUI frame should be titled “Start and Done.”
-
Modify Program 15.5 by implementing the
mouseExited(),mousePressed(), andmouseReleased()methods. Each method must display a suitable message in the text box when the corresponding event occurs. For example, when the mouse exits buttonone, the text box should display “Mouse exits One.” -
Modify Program 15.8 such that clicking the icon-decorated button plays the sound of a bat squeaking. You will need to add an
ActionListenerto the button, create an audio clip for the desired sound, and then play this clip when the button is clicked. Consider visiting Freesound.org to find free sound files. -
Write a Java program that creates a GUI containing a label with a picture of yourself.
-
Extend the
AnimalSoundsclass developed in Example 15.9 to include sounds for various animals. There are many publicly available sounds files for use in your program. The Freesound link above is only one source. -
In Example 15.9 we stopped both the chirp and the bark sounds because the action listener corresponding to the “Stop Playing” button didn’t know which sound was playing. Modify Program 15.7 so that only the sound that’s playing is stopped. You may need to declare another variable to keep track of which is playing.
-
Modify Program 15.11 so that it plays a sound associated with an animal when the mouse is clicked over its label. Note that this is an example of a situation where a
MouseListenercan be used to listen for mouse click events though anActionListenercannot. As in Exercise 15.7 and Exercise 15.9, you may need to download sounds from the Internet. -
Modify the GUI from Section 15.4 to display the problem number the user’s working on. The first problem will be numbered “Problem 1” with subsequent problems 2, 3, and so on. The number should increase each time the user hits the “Submit” button. Find a suitable place on the GUI to display this information. You may need to add a panel to reorganize the GUI.
-
Remove the
actionPerformed()anditemStateChanged()methods from theMathTutorclass given in Section 15.4. Move the code from these methods into individual anonymous inner classes added to theadd,subtract,multiply,divide, andadvancedobjects.Note that you can now remove
ActionListenerandItemListenerfrom the list of implemented interfaces for theMathTutorclass. Reorganizing the code this way should have no impact on the functionality of the program. Is doing so a good idea? Why or why not? -
In Program 15.3 exchange the first two
add()method calls on thepanelso thatthatButtonis added to the panel beforethisButton. Explain how the appearance of the GUI is changed. -
Modify Program 15.2 by adding a second panel named
secondPanel. Create a new button namedotherButtonwith the label “The Other.” AddotherButtontosecondPanel. Now addsecondPaneltoframeand look at the GUI generated. Can you explain why only components from one of the panels is visible? -
Remove the line
frame.setResizable(false);from Program 15.10. Run the modified program and resize the frame to various sizes. How does the placement of the buttons change? -
Modify Program 15.10 by deleting the lines that set the frame size. What does the resulting GUI look like? Now add the following code just before the line
frame.setResizable(false);:frame.pack();When you run the modified program, what’s the impact of using the
pack()method? -
Create a GUI with a frame that uses
GridLayoutand has a suitable size. Use a 3 × 2 layout with a horizontal and vertical spacing of 5 pixels each. Use a loop to add eight buttons to your frame, labeled 1 through 8. Observe how the frame expands to include all the buttons even though theGridLayoutonly specified 6 cells. Depending on the frame size, you might have to resize the window to see all cells and buttons. What happens if you add fewer than 6? -
Consider the calculator layout from Program 15.13. Add listeners to all of its buttons so that clicking on the number buttons, the plus and minus buttons, and the “Enter” button will make it perform like a calculator capable of addition and subtraction. Note that you’ll need to add some additional fields to keep track of the current value and whether or not the user has just pressed the plus or minus buttons.
-
Write a Java program that creates a GUI with a frame and a menu bar containing a single menu. Add a menu item to this menu. Use the
add()method, not thesetJMenuBar()method, to add the menu bar to the frame. What’s the difference between using theadd()method and thesetJMenuBar()method to add a menu bar to aJFrame?
Experiments
-
Recall that Program 15.16 is unresponsive because the event dispatch thread goes to sleep for 5 seconds (5,000 milliseconds). Experiment with this value to determine how much time you can block the EDT before the GUI feels unresponsive.
-
Program 15.16 is unrealistic because the EDT simply goes to sleep. Normally, a GUI becomes unresponsive because the EDT is performing extensive calculations or doing slow I/O operations. Replace the line that sleeps with a short loop that performs significant calculations. One simple way to spend a lot of computational time is by summing the sines of random numbers, similar to the work done in Example 13.10. How many sines do you need to compute to make the GUI unresponsive for 5 seconds?
-
Take the computationally expensive loop from Exercise 15.22 and use it to replace the line that sleeps in Program 15.17, the
SwingWorkerversion of the program. Does the program become unresponsive if you run it? If possible, run the program on Windows, macOS, and Linux environments. If it’s unresponsive in some environments but not others, why do you think that might be?
16. Testing and Debugging
I never make stupid mistakes. Only very, very clever ones.
16.1. Fixing bugs
This chapter is about finding, fixing, and preventing bugs in software. Within this book, this chapter is unique in that it’s not based on concrete problems with straightforward solutions. Finding and fixing bugs in software, especially concurrent software, is a problem no one’s solved completely. The first half of this chapter will focus on common bugs and how to fix them. The second half will focus on design techniques for preventing bugs and testing techniques for finding bugs hidden in your code.
16.1.1. Common sequential bugs
We’ll begin with bugs commonly found in sequential programs, some of which have been mentioned in previous chapters as common mistakes. We won’t discuss syntax errors or any other errors which can be caught at compile time. Instead, all bugs discussed in this chapter are run-time bugs.
There’s an infinite number of possible bugs, so they can’t all be listed. Below are a few of the most common categories of bugs to affect beginner (and occasionally veteran) programmers.
- Precision Errors
-
Floating-point numbers have limited precision inside of a computer. Programs that assume infinite precision might break when real results are slightly larger or smaller than expected.
- Overflow and Underflow
-
The cousin of limited precision in floating-point types is the limited range of values that integer types can take on. If a value goes too high, it wraps back around and becomes a negative number. If a value becomes too low, the opposite can happen.
- Casting Errors
-
Casting can have many subtle effects in a program. Sometimes programmers divide two integers and forget that the result is an integer. Incorrectly casting objects can also lead to a
ClassCastException. - Loop Errors
-
Loops are a favorite place for bugs to hide. Three of the most common loop mistakes are:
-
Off-by-one errors: The loop executes one more or one fewer time than expected.
-
Infinite loop: A classic. The loop continues executing until the program runs out of memory or a user stops the program externally.
-
Zero loop: The loop doesn’t execute even once, though the programmer expected it to.
-
- Equivalence Testing Errors
-
If a programmer uses the
==operator to compare two references, it will be true only if the two references point at the same object. Instead, theequals()method should usually be used to compare the attributes of the objects pointed at by the references. - Array Errors
-
Arrays are often involved with loop errors. Two problems specific to arrays are:
-
Out of bounds: A math mistake or an off-by-one error could lead to an attempt to access an element of an array that comes before index 0 or after the last index.
-
Uninitialized object arrays: Arrays of primitive data types can be created and used immediately; however, arrays of object types are filled with
nullvalues until each element is assigned an object, often a new object.
-
- Scope Errors
-
Some errors can be caused by a programmer’s misunderstanding about the visibility of a variable.
-
Shadowing variables: If a local variable is declared with the same name as a field or class variable, changes within a method will be made to that local variable. This principle is straightforward, but if a programmer doesn’t notice the shadow declaration, the behavior of the code can be very confusing.
-
Reference vs. value: When primitive data is passed as an argument into a method, its value is copied into the method, and the original data is unchanged. When an object is passed as an argument into a method, the reference is unchanged, but methods called on the object can still affect it.
-
- Null Pointer Errors
-
By this point in your programming experience, you’ve almost certainly experienced a
NullPointerException. This last kind of bug is, in many ways, a catch-all category because a null reference is generally not due to a simple typographical error. In the simplest case, a reference simply hasn’t been initialized with some default constructor, but more often there’s a logical error in the design of the code.
16.2. Concepts: Approaches to debugging
When you’ve discovered the existence of a bug, pinning down its cause can be difficult. There are a number of different techniques that are useful for narrowing down the possible problems.
16.2.1. Assertions
A common cause of program errors is an incorrect assumption by a programmer. A programmer can assume that the user will only enter positive numbers, that a library call won’t throw any exceptions, or that a linked list is never empty. Some assumptions are reasonable, but it’s important to make sure that they’re correct.
Using assertions is a way to check some of your assumptions, often those surrounding a method call. In most languages, an assertion tests a condition. If that condition is true, nothing happens, but if it’s false, the program shuts down or an error or exception is thrown. Using assertion statements is particularly important with methods because you want to be sure that both your input and output are in the ranges you expect them to be.
Java supports assertions natively, as we’ll discuss in the next section. However, virtually every language allows you to create your own assertions should they not be present as a language construct.
16.2.2. Print statements
Computer programs execute quickly. Even if they executed a million times slower, no human is sensitive enough to decipher the flow of electrons inside the processor as a program executes. The simple truth is that we have no idea what’s really happening when our programs execute. We believe that we understand our programs well, and the output usually confirms that our programs are doing what we imagine they should be doing.
If the output doesn’t match our expectations, we might not have enough data to understand the problem. As long as there have been programmers, they have been printing out additional debug information to find their errors. This technique can go a step beyond simple assertion statements because you can print out the values of the variables rather than just test to see if they’re in a range.
Once you’ve found the error in your code, it can be tedious to remove
all of your debug statements. Some programmers use a special print
command that can be turned off using a global variable or compiler
option. Others send their output to stderr so that it doesn’t
interfere with the legitimate output of the program. Much depends upon
the system, the language, and the individual tastes of the programmer.
16.2.3. Step-through execution
With the rise of modern debugging environments, using print statements has lost some of its appeal. Most languages allow the programmer to run his or her program in a special debug mode where it’s possible to execute a single line of code at a time. These tools usually give the option of stepping over method calls or stepping into them on a case by case basis.
As the program executes, the programmer can inspect the values of the variables in the code. This method of debugging is excellent because it allows the programmer to watch the execution of the code at whatever pace he or she desires. Pinpointing problems becomes trivial if you know which variables you need to watch.
Despite the power of this technique, it has critics. Some older programmers look down on these tools because they make new programmers lazier and, in some cases, less careful about writing code correctly in the first place. It should be noted that step-through execution modes are not available for every language or for every system. Some embedded software or operating system programming cannot be debugged on the real hardware in this way. Of course, most of these systems can be run in virtual environments that do allow step-through debugging.
Even when step-through debugging is available, there are difficulties
that can limit its effectiveness. If the bug occurs sporadically,
perhaps due to race conditions, a programmer might not know where to start
looking. Certain data structures such as the list template in C++ might
not be easily traversable using the inspection facilities of the
debugger. Likewise, the bug or the source of the unexplained behavior
could be buried in library code. The debugger doesn’t always have
access to library code for stepping through.
16.2.4. Breakpoints
Breakpoints are a feature of step-through debuggers designed to make them easier to use. A user can specify a particular line of code (with some restrictions) as being a place where the debugger should pause execution. Debuggers typically rely on at least one breakpoint in order to skip all the preliminary parts of the code and skip straight to the perceived trouble spot.
Sometimes an error will crop up predictably after many thousands of iterations of a loop or unpredictably due to race conditions or user input. For either of these cases, conditional breakpoints can be used to save the a programmer a great deal of time. Rather than always pausing execution on a given line, a conditional breakpoint will only pause if a certain condition is met.
16.3. Syntax: Java debugging tools
16.3.1. Assertions
As we mentioned before, many languages have assertions as a built-in language construct. In Java, there are two forms this feature takes. The simpler can be done by typing the following.
assert condition;In this case, condition is a boolean value that’s expected to be true
for the program to function properly. The more complicated form of the
feature can be used as follows.
assert condition : value;This form adds a value that can be attached to the assertion to give the user more information about the problem. This value can be any primitive data type, any object type, or a statement that evaluates to one of the two.
If you’ve never used an assert statement before, you might want to
test it out by forcing an assertion to fail. You might try the following.
int x = 5;
assert (x < 4) : "x is too large!";Then, if you compile your program and run it through the JVM, you’ll
be shocked when absolutely nothing happens. Actually, some of you with
older Java compilers might have heard complaints when you tried to
compile this code. If you have a Java 1.3 compiler or earlier, it’ll treat
assert like an identifier. Some old Java 1.4 compilers might also give
warnings or require special flags to compile. However, if you
have an up-to-date compiler, the problem is that the JVM must have
assertions enabled at run time. Assertions are intended to be a special
debugging tool and ignored otherwise. To turn run program
AssertionTest with assertions enabled, type the following.
java -ea AssertionTest
With this option, an exception should be thrown at run time.
Exception in thread "main" java.lang.AssertionError: x is too large!
If you’re using an IDE like Eclipse or IntelliJ, you’ll need to enable
assertions on the run configuration for the program, usually by putting -ea
in the field for JVM arguments. There are other options allowing you to
enable or disable assertions for specific packages or classes.
Now that you know how to use assertions, you need to know when they’re
a good idea. The Java Tutorials
on the Oracle website suggest five situations
where assertions are useful: internal invariants,
control-flow invariants, preconditions for methods, postconditions for
methods, and class invariants. Internal invariants are those
situations when you assume that reaching a certain place in your code,
like the else branch of an if statement, will force a variable to
have a certain value. For internal invariants, you assert that the
variable has the expected value. A control-flow invariant means that
you assume that your code will always execute along a certain path. For
control-flow invariants, you assert false if the JVM reaches a point
in the code you expected it never would. Method preconditions are
those conditions you expect to be true about the state of objects or the
input to a method before the method is called.
The philosophy of Java is that public methods should not have
assertions used to test their preconditions. Instead, illegal input
values for a public method should cause exceptions to be thrown, so
that improper usage can always be dealt with. In contrast, method
postconditions are the states that various variables and objects should
have at the end of a method call. Using assertions to check these values
is fine, since they reflect an error on the part of whoever wrote the
method. Class invariants are conditions about the state of every
instance of a class that should be true as long as the class is in a
consistent state. Perhaps a method call rearranges the innards of an
object, but by the end of the method call, the object should be
consistent again. You should use assertions to check class invariants at
the end of every method that could make the object violate these
invariants.
Wonderful as assertions are, there are times when they shouldn’t be
used. The key danger of assertions is that they’re usually turned off.
Thus, any statement that’s part of an assertion must not have
side-effects that are necessary for the normal operation of the program.
For example, imagine you have an object called bacteria that
mutates periodically. The mutation returns true if successful and
false if there was an unexpected error. You should not test for that
failure inside an assert, as follows.
assert bacteria.mutate() : "Mutation failed!";With assertions disabled, the entire assertion is skipped, and the
bacteria object won’t mutate.
Instead, your assertion should test only the result of the computation.
boolean success = bacteria.mutate();
assert success : "Mutation failed!";As stated above, checking for bad input coming into public methods
shouldn’t be done with assertions because turning off assertions will
remove your error checking.
16.3.2. Print statements
Print statements are one of the most time-honored methods of debugging and remain a quick, dirty, yet effective means of finding errors. Java does not provide any special tools to make print statements easier to use for debugging. Some purists might argue that this kind of debugging which focuses on progressively narrowing down the location of a problem until the bad assumption, logical mistake, or typographical error can be found should be done only with assertions.
Nevertheless, there are a few tips to make print statements a better
debugging tool in Java. The first is the use of System.err. By now,
you’ve used System.out.print() and System.out.println() so many
times that you’re probably tired of them. Any output method that can be
used with System.out can also be used with System.err. For example,
there’s a System.err.print() and a System.err.println() method. If
you simply run a program from the command line and watch the output, you
should see no difference between using System.out and System.err.
However, if you redirect the output of your program to a file using the
> operator, only the System.out code will be sent to the file.
Anything printed with System.err will be sent to the screen.
Alternatively, you can redirect System.err to a file by using the 2>
operator. Using System.err makes it easier to separate legitimate
output from error messages, but it also makes it easier to comment out
your debug code by doing a find and replace.
A more extensive method for using print statements to debug is by
defining your own class for printing. Every method in it can call a
corresponding method in System.out or System.err. You can define a
boolean value at the class level that determines whether or not
methods in your debug printing class print or stay silent. When you want
to change from debugging to your production or retail version of the
code, you can simply switch this value to false.
A “modernized” method of using print statements is creating a simple
GUI instead. In preparing materials for this textbook, we were
occasionally frustrated by the fact that multiple threads can interfere
with each other while printing on the screen: You can’t always tell
which thread is printing which characters. By displaying the output of
each thread in separate JTextArea or JLabel components on a simple GUI,
you can disentangle the output of each thread.
16.3.3. Step-through debugging in Java
Since the Eclipse and IntelliJ IDEs are so widely used, we’re going to review the step-through debugging features of each environment. Similar tools are available with other IDEs and for most languages.
Eclipse
In Eclipse, you can set set breakpoints either by right clicking or double clicking on the shaded bar immediately to the left of the line you’re interested in or by selecting Toggle Breakpoint from the Run menu. If you try to set a breakpoint on an empty or ineligible line of code, Eclipse will set it on the next legal one.
To debug a program in Eclipse, right click on the file you wish to run in the Package Explorer and select Debug As Java Application. If your program’s already set up to run, you can simply click the Debug button in the toolbar. Whenever you hit a breakpoint, Eclipse will switch to the Debug perspective if it’s not already there.
Once execution is suspended on a breakpoint, you can use the commands Resume, Step Into, Step Over, and Step Return, either from the Run menu or from the toolbar. The Resume command (or F8) allows the program to continue execution, until it hits another breakpoint. The Step Into command (or F5) advances the execution of the program by one statement, moving into a method is there is a method call. The Step Over command (or F6) also advances the execution of the program by one statement, but it skips over method calls. The Step Return (or F7) command advances the execution of the program to the end of the current method and returns, popping the current method off the stack. In the Run menu, there’s also a useful Run to Line command, which will run code until execution reaches the line where your cursor is.
By right-clicking on a breakpoint in Eclipse, you can access its properties. Though properties, you can specify that a breakpoint only halts execution when a specific condition is true or only for a specific thread. Eclipse also provides variable watch and inspection options. Simply by hovering over a variable, its type and value are displayed. You can also inspect an object and traverse its fields. The Variables pane will show the values of local variables, and the Breakpoints pane will show active and inactive breakpoints.
The Debug pane will show a view of the stack for each thread. By moving up and down the stack, the local variables will change depending on which method call you’re currently inside of. By default, the method call displayed will be wherever code most recently executed, but it’s useful to jump back to the method that called the current method (and the method that called that, and so on) to better understand the overall state of the program and why the current method call has the parameters that it does.
IntelliJ
The debugging facilities provided by IntelliJ are similar to those found in Eclipse, and many developers prefer them. You can click in the space to the left of a line of code to set or remove a breakpoint, and you can edit its properties with a right-click.
You can start your program running in debug mode by clicking the Debug button on the toolbar or selecting Debug (Shift+F9) from the Run menu. When execution of your program reaches a breakpoint and pauses, you can use essentially the same tools to advance execution as you would in Eclipse.
The Resume Program command (or F9) will continue execution. The Step Into command (or F7) will advance execution by one line, moving into a method call if there is one. IntelliJ also has a Smart Step Into command (or Shift+F7) that allows you to pick which method call to step into if there’s more than one on the next line. The Step Over command (or F8) advances execution by one line but does not move into a method call. The Step Out command (or Shift+F8) returns from the current method. IntelliJ also has a Run to Cursor command that will try to execute code until reaching the line where your cursor is. All of these commands can be found in the Run menu, and the most common ones appear on toolbars.
In addition, IntelliJ has “force” versions of most of these commands which step over a line of code, step into a method call, or run to your cursor, ignoring breakpoints that might pause execution.
IntelliJ has a Frames pane similar to the Debug pane in Eclipse. It allows
the user to select a given thread and jump to different method calls in the
stack for that thread. Likewise, IntelliJ has a Variables pane that shows the
state of the local variables for the current method call. One of the features
that developers like the most about IntelliJ is that it displays the values that
variables have on each line where they’re used. In other words, a line of code
that adds variables x and y will display their values off to the side of the
line of code, updating the display each time the line’s executed.
16.3.4. Examples
Experience is often the difference between a good programmer and a bad programmer. Having seen a bug before means you know to expect it in the future. Don’t be discouraged if it takes hours to find a bug and squash it. Although that time is stressful, spending hours poring over your program makes you better at reading code, a skill just as valuable as writing code. And when you’ve spent hours trying to fix a simple mistake, you’re unlikely to make the same mistake again. To make it easier to spot some of these mistakes, we give a few examples corresponding to the common bugs listed in Section 16.1.
Floating-point precision can cause subtle errors.
Here’s an example of a program attributed to Cleve Moler that gives
some estimation of the threshold for floating-point precision. Note that
a ≈ 4/3, making b ≈ 1/3, c
≈ 1, and d ≈ 0. Nevertheless,
the comparison d == 0.0 in the if statement in this code will
evaluate to false.
double a = 4.0 / 3.0;
double b = a - 1;
double c = b + b + b;
double d = c - 1;
System.out.println(d);
if(d == 0.0)
System.out.println("Success!");The output for this fragment is -2.220446049250313E-16, and it would be
much worse with float variables. Computer scientists who specialize in
numerical analysis have tricks for minimizing the amount of floating-point
error introduced, but awareness is an easy solution to these kinds of bugs.
When testing for specific values of a floating-point number, it’s wise to
test for a range rather than a single value. For example, the condition
d == 0.0 could be replaced by Math.abs(d) < 0.000001.
As you know, the int and long types have limited bits for
storage. If an arithmetic operation pushes the value of an int
variable larger than Integer.MAX_VALUE, the variable will come full
circle and become a negative number, usually with a large magnitude. The
converse happens when a variable is pushed lower than the smallest value
it can hold. These situations are called overflow and underflow,
respectively, and Java throws no exceptions when they occur. Programmers
who deal with large magnitude values in int or long types get used
to underflow and overflow, and when unexpected values are output by
their programs, they’re usually quick to pin down the problem variable.
Overflow and underflow can cause more surprising bugs when programmers
forget the sharply limited range of values for byte and char types. For
example, a curious beginner programmer might want to print out a table
of all of the possible values for char. Perhaps the programmer has
forgotten the range of values a char can take and is stumped when
the following loop does not terminate.
for(char letter = '\0'; letter < 100000; letter++)
System.out.print(letter);Each time letter reaches Character.MAX_VALUE which is '\uFFFF' or
65535 as a numerical value, the next increment pushes its value back
to 0. These kinds of errors with byte and char values are most
common when they’re being used as numbers. Some
possibilities are cryptography, low level file operations, and manipulation
of multimedia data. The best solution is care and attention. It can help
to store the values in variables with more bits such as int or long
values, but care must still be taken to ensure that these values are
within the appropriate range before storing them back into variables
with a smaller number of bits.
For example, color values in many image formats are stored as red, green
blue values with a byte used for each of the three colors. In this
system, the darkest color, black, is represented as (0,0,0), zero
values for each of the three byte values. At the same time, the lightest
color, white, is represented conceptually as (255,255,255). In
principle, we can perform a simple filter to increase contrast and
lightness by doubling all the pixel values. Given red, green, and
blue color values stored in three byte variables called red,
green, and blue, a naive implementation of this filter might be as
follows.
red *= 2;
green *= 2;
blue *= 2;In Java, this code would not function correctly. The first problem is that, even
though image standards are written with color values between 0 and 255,
Java byte values are signed. The web standard for the color purple
has red, green, and blue values of (128,0,128). Since Java byte
values are signed, printing the byte values for each component of
purple directly will actually print (-128,0,-128). Multiplying the
green value by 2 still gives 0. However, multiplying -128 by 2 as a
byte value is -256 which underflows back to 0. Thus, “brightening”
purple actually turns it into (0,0,0), black. Properly applying the
filter to a byte requires a conversion to the int type, masking out
the sign bit, scaling by 2, capping the values at 255, and then casting
back into a byte. Despite the complicated description, the code is not
too unwieldy.
// Bitwise AND automatically upcasts to int
red = (byte)Math.min(255, 2*(red & 0xFF));
green = (byte)Math.min(255, 2*(green & 0xFF));
blue = (byte)Math.min(255, 2*(blue & 0xFF));The previous example about scaling color component values shows one of the
dangers of casting. Someone can easily forget that the implicit cast to
convert a byte to an int always uses a signed conversion. Likewise, the
explicit cast needed to store an int into a byte will cheerfully convert
any arbitrarily large int into a byte, even though the final value might
not be expected by the programmer.
Many other casting errors commonly crop up. The most classic example might be muddling floating-point and integer types.
int x = 5;
int y = 3;
double value = 2.0*(x/y);Above, it’s easy for a programmer to forget that the division of x
and y is integer division. After all, the 2.0 is right there,
causing an implicit cast to double. Of course, this cast happens after
the division, and the answer stored into value is 2.0 and not the
3.3333333333333335 that the programmer might have expected.
Newer programmers sometimes forget that an explicit cast from a floating-point type to an integer type always uses truncation, never rounding.
int three = (int)2.99999;This assignment will always store 2 into three. The Math.round()
method or some other additional step is needed to perform rounding.
Casting errors are not limited to primitive data types. Object casting will be discussed at length in Chapter 17. The biggest danger there is an incorrect explicit upcast.
Fruit snack = new ChiliPepper();
Apple apple = (Apple)snack;In a botanical sense, a chili pepper is indeed a fruit and its parallel
Java class is apparently a child of the Fruit class. For some reason,
the programmer thought that the only Fruit that would be pointed at by
a snack reference would be of type Apple. Instead of a mouth on
fire, the programmer gets a ClassCastException. This two line example
is so simple that it should never come up in serious programming. A much
more common example is an array or linked-list whose contents have a type
that’s the parent class of the item you generally expect to be stored. If a large
team is working on a body of code with such a list, half of the
team might expect the list to contain only Apple objects while the
other expected only ChiliPepper objects. The use of generics,
discussed in Chapter 18,
can reduce the number of casting errors of this kind, but some applications require a
list to hold many different types with a common superclass. In those
cases, some amount of explicit (and therefore dangerous) casting will
usually be necessary when retrieving objects.
Loops give Java much of its expressive power, which includes the power to express incorrect code. Here are examples of a few of the most common loop errors.
Computer scientists often use zero-based counting. This departure from “normal” practices is just one source of loops that iterate one time more or less than they should. If you want to iterate n times, a good rule of thumb is to start at 0 and to go up to but not including n. Alternatively, if you have a reason not to be zero-based, you can start at 1 and go up to and including n.
for(int i = 1; i < 50; i++)
System.out.println("Question " + i + ".");Perhaps you want to make a template for an exam. Instead of being zero-based, you start at 1 because most exams don’t have a Question 0. Unfortunately, you’ve gotten so used to using strictly less than for your ending condition that you forget to change it and only get 49 questions printed out. If your purpose was making an exam, you could catch your mistake and move on. If you’re writing a program that dispenses a quantity of heart medication into a patient’s IV in a hospital, one iteration too few or too many could cause the patient to get too little of the drug to make a difference or too much of the drug to be safe.
Input is another tricky area when it comes to being off by one.
int i = 0;
double sum = 0;
int count = 0;
Scanner scanner = new Scanner(System.in);
while(i >= 0) {
sum += i;
System.out.print("Enter an integer (negative to quit): ");
i = scanner.nextInt();
count++;
}
System.out.println("Average: " + (sum / count));This fragment of code appears to be a perfectly innocent loop that finds
the average of the numbers entered by a user. The loop uses a sentinel
value so that the user simply enters a negative number when all the
numbers have been entered. The value of sum is updated before the user
enters a value; thus, the harmless 0 from the declaration of i is
included but the final negative number entered to leave the loop is not.
Unfortunately, the value of count is incremented for every turn of the
loop, even the extra one for the negative number. To combat this
problem, an if statement could be used inside of the loop or count
could simply be initialized to -1. The mistake is a simple one, but it
doesn’t jump out at you unless you trace a few executions. What’s most
insidious is that the error is going to be small, especially for large
sets of input numbers. Catching this kind of bug will be discussed more
throughly in the second half of this chapter which deals with testing.
Infinite loops come in many different flavors, from the char overflow
example earlier to traversing a linked-list which has a cycle in it.
Many infinite loops are caused by simple typographical errors. Perhaps
the most classic is:
int i = 1;
while(i <= 100);
{
System.out.println(i);
i++;
}It’s usually a beginning programmer who leaves a semicolon at the end of
the while header, but even veterans can get overly enthusiastic
about semicolons. Often a programmer confronted with such a bug (which
causes no output, in this case) will scour the body of the loop without
carefully scrutinizing the condition. An extra semicolon at the end of
a for loop header will usually cause an error but will usually not
cause an infinite loop.
public double average(int[] array) {
double sum = 0;
int count = 0;
for(int i = 0; i < 100; i++) {
sum += array[i];
count++;
if(i == 0)
i--;
}
return sum / count;
}This example might be too absurd to appear in a
textbook, but nearly everyone has written worse code while learning to
program. We could suppose that this method is meant to average the
values in an array, but for some reason, zero valued entries are not to
be counted. The student probably meant to have the following if
statement.
if(array[i] == 0)
count--;Those two small changes turn the method into a working but slightly
inelegant solution. When debugging remember that index variables in
for loops can get changed in the body of the loop and change the
expected behavior. Generally, it’s a bad idea to change the value of an
index variable anywhere other than the header of a for loop, but there
are times when doing so gives the cleanest solution.
Many loop errors are caused by a bad header. Getting the inequality backward or switching increment and decrement will usually make a loop that runs a very long time or not at all. We’ll see the second possibility just a little later.
for(i = 10; i > 0; i++)
System.out.println(i + "!");
System.out.println("Blast-off!");In this case, the programmer clearly wanted to count down from 10 to
1, but after so much incrementing, he or she forgot to make i
decrement. As a result, the value of i increases for a very long (but
not infinite) time, until it overflows.
On the other end of the spectrum, a bad condition can make a loop
execute zero times on for and while loops. For some input, doing so
might be intended behavior. In other cases, no input will ever cause the
loop to execute.
int i = 0;
double sum = 0;
int count = -1;
Scanner scanner = new Scanner(System.in);
while(i > 0) {
sum += i;
System.out.print("Enter an integer (negative to quit): ");
i = scanner.nextInt();
count++;
}
System.out.println("Average: " + (sum / count));We’ve returned to our earlier example of averaging a set of
numbers input by the user. This time we’ve initialized count to be -1
to avoid the off-by-one error, but we’ve also changed the inequality
of the while loop from greater than or equal to strictly greater. As a
consequence, the loop is never entered because 0, the initial
value of i, is too small.
public static boolean isPrime(int n) {
for(int i = 1; i < n; i++) {
if(n % i == 0)
return false;
}
return true;
}Here’s a simple method intended to test the number n for primality.
Unfortunately, the programmer started the index i at 1 instead of 2.
As a consequence, this loop will only run once before finding that any
number is divisible by 1. True, this is not a loop that executes zero
times, but only once is still just as wrong.
public static boolean isPrime(int n) {
for(int i = 2; i < n; i++) {
if(n % i == 0)
return false;
else
return true;
}
}This example is similar code trying to solve the same problem.
Again, the loop only runs once because the programmer forgot that
finding a single case when a number is not evenly divisible by another
number does not make it prime: a large range of possible factors must be
checked before we can be sure. Many, many beginning programmers make
this mistake when asked to solve this problem. Perhaps some insight
about the nature of bugs can be gained from this example. By the time a
student writes a program of this kind, he or she should have a fair idea
of how for loops and if statements work. Likewise, the student will
have a fair understanding of the notion of primality. Yet in the
process of combining the ideas together, it’s easy to get sloppy and
write incorrect code that gives some semblance of being correct.
Equivalence is tricky in Java. Very inexperienced programmers confuse
the = operator with the == operator, but using the == operator to
test for equivalence between two references causes more (and subtler)
problems. Comparing two references with the == operator will evaluate
to true if and only if the two references point at the exact same
object.
String string1 = new String("Test");
String string2 = new String("Test");
if(string1 == string2)
System.out.println("Identical");
else
System.out.println("Different");Because these two String references point to two different String
objects, which happen to have identical contents, the == returns
false, and the output is Different. With String objects this matter
is further confused by a Java optimization called String pooling.
String string1 = "Test";
String string2 = "Test";
if(string1 == string2)
System.out.println("Identical");
else
System.out.println("Different");Because Java keeps a pool of existing String values, only one copy of
"Test" is in the pool, and both string1 and string2 point to it.
Thus, this second fragment of code prints Identical. Because of
String pooling, programmers can write code which can work in some
situations and fail in others, if it depends on the == operator.
For String objects as well as every other reference type, it’s
almost always the case that the equals() method should be used to test
for comparison instead of the == operator. There are a few instances
when it’s necessary to know if two references really and truly do refer
to the same location in memory, but these instances are a tiny
minority.
That said, the equals() method is not bullet-proof. With String
objects and most of the rest of the Java API, you can expect good
behavior from the equals() method. However, if you create your own
class, you’re expected to implement the equals() method. By default,
the equals() method inherited from Object only does an equality test
using ==.
Properly implementing the equals() method takes care and thought. If
your class contains references to other custom classes, you must be
certain that they also properly implement their own equals() methods.
Likewise, to conform to Java standards, a custom equals() method
implies that you have also implemented a custom hashCode() method so
that objects that are equivalent with equals() give the same hash
value. It seems nit-picky to mention this issue, but many real-world
applications depend on the efficient and correct operation of hash
tables. Hash tables are data structures used to store and
retrieve a key and an associated value. We’ll discuss them briefly
in Example 18.4.
16.3.5. Array errors
Any time you have a large collection of data, there are always opportunities for bugs. With catastrophic array bugs, Java usually gives clear exceptions that point you to the line number. Once the exception is thrown, the bug should be obvious. The biggest difficulties arise when some unusual course of events is responsible for the bug cropping up and you have to reconstruct what it is.
We have all experienced an ArrayIndexOutOfBoundsException. Either a
little carelessness with our indexes or a mistake about the size of the
array can lead us to try to access an index that isn’t in the array.
In the C language, a negative index is sometimes a legal location, but it
never is in Java. Although errors involving negative indexes sometimes occur
in code, a more common error is accessing an index slightly larger than the
bounds of an array, particularly with a loop.
int[] array = new int[100];
for(int i = 0; i <= 100; i++)
array[i] = i;In this example, the last iteration of the loop will access index 100
when array only goes up to index 99.
The causes for going out of bounds can be more subtle. We can imagine an
array of linked lists, perhaps for storing English words in a dictionary. If we
want to select a list based on the first letter of the word, we could use
an array of length 26. Consider the following helper method used to add a
new String to the correct list.
public void add(String word) {
int index = word.toLowerCase().charAt(0) - 'a';
lists[index].add(word);
}We can assume that the add() method for a given linked list works
properly, but we might have caused other problems already. For one thing,
we assumed that word began with either an upper- or lowercase letter,
corresponding to our array locations 0 through 25. We’re depending on
other code to check the input and throw out String values
like "$1" or "-isms", which would map to indexes outside of the 0 to 25
range. Incidentally, we’re also assuming that word has at least one character
in it. Even if we expect the input to the method to be error free, the addition
of error checking is rarely a bad idea.
Another simple mistake that can occur with arrays is failing to
initialize an object array. With a primitive data type like int,
creating an array with 1,000 elements automatically allocates enough
space to hold those elements and even initializes each one to a default
value, 0 in the case of an int. With an object data type, however,
each element of the array is a reference to null until it’s
initialized.
Hippopotamus[] hippos = new Hippopotamus[15];
hippos[3].feed();This example causes a NullPointerException. New programmers are often
confused by this error because they expect the exception to mention the array
or its indexes. For more experienced programmers, this kind of mistake is
more of a forehead-slapping oversight than a mind-numbing puzzler that’ll take
hours to debug. It’s probably just a matter of instantiating each element in
the array before you try to feed those hungry, hungry hippos.
Hippopotamus[] hippos = new Hippopotamus[15];
for(int i = 0; i < hippos.length; i++)
hippos[i] = new Hippopotamus();
hippos[3].feed();16.3.6. Scope errors
We don’t have variables in real life, and as a consequence, our intuition about them is sometimes wrong. Which variable you’re accessing at any given time can appear obvious, even if it really isn’t.
Java allows variables in different scopes to be declared with the same identifier. If the scopes are two separate methods, then they’ll never interfere with each other. However, if one scope encloses another, the inner variable will shadow or hide the outer variable.
public class Shadow {
int darkness = 10;
public void deepen(int darkness) {
darkness += darkness;
if(darkness > 100)
darkness = 100;
}
public int getDarkness() { return darkness; }
}In this example, the field darkness is being shadowed by the local
variable darkness in the deepen() method. It appears that the
programmer wanted to increase the field darkness by the amount passed
into the parameter darkness and failed to notice that both variables
have the same name. As a consequence, the parameter darkness will
double itself and then never be used again while the field darkness
will never increase. This kind of bug could go uncaught for a long while
until a programmer notices that the Shadow object isn’t increasing in
darkness no matter how many times it’s told to.
This mistake is also common in constructors, since it’s
reasonable to give a certain parameter a name similar to the field it’s
about to initialize. Some programmers explicitly prefix all fields with
this even though it’s often redundant. Three additions of this will
fix the problem in the preceding example.
public void deepen(int darkness) {
this.darkness += darkness;
if(this.darkness > 100)
this.darkness = 100;
}In Java, scope is also defined in terms of classes and their parent classes. A parent class variable can be shadowed by a child class variable of the same name.
public class Bodybuilder {
public int strength = 8;
public boolean isStrongEnough(int strengthNeeded) {
return strength >= strengthNeeded;
}
public void setStrength(int value) { strength = value; }
}public class BraggingBodybuilder extends Bodybuilder {
public int strength = 10;
public void brag() {
System.out.println("My strength is " + strength + "!");
}
}This example looks like a simple case of inheritance, but whoever wrote
the BraggingBodybuilder class mistakenly included the
field strength again. As a consequence, any BraggingBodybuilder will
always brag that his or her strength is 10, even when code sets his or
her strength to other values. When strength is tested, it’ll use the
strength field from the superclass Bodybuilder which is set by the
setStrength() method. When classes have large numbers of fields,
making such a mistake becomes easier.
Dynamic and static binding complicate this scope problem further. The fragment of code below using the class definitions from above highlights these complications.
Bodybuilder builder = new BraggingBodybuilder();
builder.strength = 15; (1)
BraggingBodybuilder bragger = (BraggingBodybuilder)builder;
bragger.brag();
bragger.strength = 20; (2)
bragger.brag();| 1 | Because fields are statically bound to the class of the
object, the strength field for Bodybuilder will be set to 15. |
| 2 | However, the strength field for BraggingBodybuilder
will be set to 20 here. |
Thus, the first call to brag() will print out My strength is 10!, but the
second call will print out My strength is 20!. Note that some of the
confusion in this example is possible only because the field strength is
public. If the field was private and only changed through methods, at
least there would no longer be two ways to set the strength field with
two different outcomes.
The final category of scope error we’ll talk about occurs when using methods because of confusion between passing by reference and passing by value. Every variable in Java is passed by value. However, when that value is itself a reference, it’s possible to change the values that it references.
public void increaseMagnitude(int number) {
number *= 10;
}A novice Java programmer might write a method like the above, expecting
the value of number to increase by 10 in the calling code. Some
languages like Perl use call by reference as default. Other languages
like C++ and C# allow the user to mark certain parameters as call by
reference. Programmers comfortable with such languages might be confused
about the workings of Java.
On the other hand, becoming used to the pass-by-value style of Java can cause other errors.
public void increaseMagnitude(int[] numbers) {
numbers[0] *= 10;
}In this contrasting example, the 0 index element of numbers is increased
by a factor of 10. Unlike the previous code, the increase in the value
of that element will affect the array passed in by the calling code. The
values in the array are shared by the increaseMagnitude() method and
the calling code. As you can see, the variable numbers isn’t changing.
Reassigning the array reference to a difference array reference would have
no affect, but we’re changing an element in the array, not the array
reference. The same phenomenon can occur with the fields of objects whose
references are passed into a method.
16.3.7. Null pointer errors
Null pointer errors usually raise a NullPointerException in Java. This
category of errors is something of a catch-all that could happen for
many different reasons, some of which have already been mentioned.
A NullPointerException could be raised because the elements of an object
array haven’t been initialized. Scope problems could cause a reference to
be null if the programmer was mistakenly updating another reference,
leaving the reference in question uninitialized.
Though they are common, it’s difficult to give a blanket explanation for
why most null pointer errors happen. Usually there’s some fundamental
error in program logic. Linked lists and tree structures that rely on
null references to mark the end of a list or an empty child node are
especially susceptible to these errors.
One significant source of errors is careless usage of method parameters.
A programmer might pass in objects that don’t conform to expectations
or even null references instead of objects. Well written
methods, particularly library calls, should be designed to throw an
appropriate exception when this happens. Poorly designed code might
blindly use a null reference without checking it first, causing a
NullPointerException.
16.4. Concurrency: Parallel bugs
We’ll discuss parallel bugs briefly here because we’ve already spoken in depth about the dangers of parallel programming in Chapter 14. Beyond deadlocks and livelocks, a key difficulty with parallel bugs is that they can make the appearance of sequential bugs nondeterministic and unpredictable.
16.4.1. Race conditions
A race condition describes the situation when the output of a program is dependent on the timing of the execution of two or more threads. Because of the complexity of the JVM and the OS and the fact that many other processes might be running and interacting, it’s usually impossible to determine how two threads will be scheduled. As a consequence, if the output of the program depends on unpredictable timing, the output will also be unpredictable.
In Java, the way that race conditions often impact the program is through some variable shared between multiple threads. When the schedule of threads becomes unpredictable, the changes made to this variable can come out of sequence, and its value becomes unpredictable. Incorrect output means that your program has a bug, but the most frustrating aspect of race conditions is that they’re nondeterministic. Your program could sometimes have the right answer and sometimes not. Your program could always have the wrong answer but not always the same one. The truly insidious issue with race conditions is that they’ll usually cause errors only a tiny percentage of the time. Thus, rigorous testing such as we’ll discuss in the second half of this chapter is necessary to show that a race condition is occurring.
16.4.2. Deadlocks and livelocks
Both deadlocks and livelocks describe situations in which some part of your program will stop making progress because of thread interaction. In the case of deadlock, there will be a circular wait in which thread A is waiting for thread B which is waiting, directly or indirectly, on thread A. In the case of livelock, some repetitive pattern of waiting for a condition that will never be satisfied is still going on, but the threads continue to use CPU time and aren’t simply waiting.
If your program reaches a deadlock state, it won’t terminate. If
threads updating a GUI become deadlocked, your window might freeze.
Typically, deadlocks are nondeterministic and occur only some of the
time. Like all race conditions, they can be difficult to detect and
duplicate. In fact, Thread.stop(), Thread.suspend(), and
Thread.resume(), three seemingly useful and fundamental methods that
were originally part of the Java Thread class, have been deprecated
because they are deadlock prone.
16.4.3. Sequential execution
One bug that isn’t even a bug in non-parallel code is sequential execution. This situation arises when, usually due to overuse of synchronization tools, parallel code runs sequentially. Each segment of code, instead of running in parallel, is forced to wait for another to complete. A certain amount of serial execution is necessary to maintain program correctness and avoid race conditions, but Amdahl’s Law gives a rigid, mathematical characterization of how easily speedup can be lost if serial execution makes up large portions of program execution. Because setting up threads and using other concurrency tools has some overheard, a parallel program executing sequentially often runs more slowly than a completely sequential version.
Since programs are usually parallelized for the sake of speedup, it’s useful to time sections of programs to see how well you’ve parallelized them. Sequential execution due to synchronization tools is only one of the many problems that can cause slow execution. The threads might be competing for a limited resource such as an I/O device or might be fighting over a small section of memory, causing cache misses. Tuning applications for maximum performance requires an expert understanding of the concurrency issues within software as well as the underlying OS and hardware characteristics. For now, it’s enough to be aware of the risk of sequential execution and to be as careful as possible when applying locks and other synchronization tools.
16.5. Finding and avoiding bugs
What would you do if you wanted to design software for a system that administers a dose of radiation to a specific location on a patient to help treat them for cancer? Depending on the specification of the problem, you might need to control various voltage sources, read data from sensors, and create a command-line interface or a GUI. With a well-designed specification, you could probably apply your knowledge of loops and control structures to an API and develop a software solution that met requirements, provided that an appropriate hardware platform existed.
But how would you know that it worked? Sure, you could run a series of tests, but how many tests would it take for you to be convinced that it worked perfectly? What if your grade was dependent on it working without a single error? Or your job? Or your life?
You’ve probably already faced the stress of trying to get a program to work as well as possible for the sake of your grade. It’s not such a far cry to imagine your job being on the line if you make a serious mistake as a professional programmer. But what about your life? Perhaps you’ll never put your own life into the hands of code you write, but odds are that you’ve already put your life into the hands of someone else’s code. Software controls airplanes, automobiles, medical equipment, and countless other applications where a bug in the code could result in loss of human life.
Sadly, there have already been cases when such bugs have surfaced with deadly consequences. One of the most famous examples of the dangers of badly written software is the Therac-25. The Therac-25 was a machine designed to deliver therapeutic radiation for medical purposes. Between 1985 and 1987, use of the Therac-25 caused at least six incidents of massive radiation overdoses, leading to at least three deaths.
Like most failures of this magnitude, there was more than a single cause behind the Therac-25 tragedies. For one thing, the machines did give an error code. However, the user manual did not explain the error code, and the technicians were not trained to deal with the errors. Even when patients complained about pain caused by the machines, the technicians and even the manufacturers of the Therac-25 were confident that the machine was operating correctly because neither of the previous models, the Therac-6 and the Therac-20, had suffered any problems. Overconfidence has played a significant role in many of the worst systems failures, including the devastating Chernobyl disaster.
Ignoring the human errors, a number of software errors were also responsible for the Therac-25 overdoses. The overdoses occurred when technicians made incorrect keystrokes giving confusing instructions to the Therac-25 about which mode of operation it should be in. In this situation, the machine would operate with a high-power beam but without the beam spreader that was necessary for its safe operation. The designers ignored the possibility that this series of keystrokes would happen. Also, a race condition was involved in this bug since it depended on one task that set up the equipment and another that received input from the technician. This race condition wasn’t caught during testing because only technicians with long practice could work fast enough to cause the bug. Finally, a counter was incremented for use as a flag variable, but arithmetic overflow occasionally caused this flag to have the wrong value.
In the remaining half of this chapter, we’ll discuss a number of testing methodologies and design strategies to minimize errors in software.
16.6. Concepts: Design, implementation, and testing
Unfortunately, there’s no foolproof way to design software. There are many researchers who work to design new languages and new development tools to limit certain kinds of mistakes, but it’s impossible to design a language as powerful as Python or Java which will also prevent all software bugs. A consequence of the halting problem, a fundamental concept in the theory of computation, is that there’s no way to design a test that will detect all potential infinite loops (or infinite recursion) for all programs.
With careful design, implementation, and testing, most errors can be reduced almost to nothing. In the following subsections, we’ll discuss these three aspects of programming and how you can apply them to writing better programs.
16.6.1. Design
We’ve remarked in the past that good design pays off ten-fold in implementation, and that payoff continues to increase by factors of ten as you move on to testing and eventually deployment.
One of the first design decisions you might have to make is choice of
language. Some languages are better designed for certain tasks than
others. For example, languages like Ada have been carefully designed to
minimize programming mistakes such as mis-matched else blocks. Many
functional languages like ML are designed so that memory errors such as
a NullPointerException are impossible. Even Java has taken clear steps
to avoid some of the errors possible, such as bus errors, in C and similar
languages that allow pointer arithmetic. However, many other factors such
as portability, compatibility, and speed will affect your language
choice.
If you’re working in the software development industry, you might be given a specification from your client or your supervisors. As you design the software needed to meet the specification, you might use UML diagrams to map out the classes and interactions you plan to implement in your program.
There are many questions you might ask yourself as you design your solution. Will your solution be compatible with the system and future changes made to the system? Is it easy to add features to your solution? Does your solution deal gracefully with mistakes in user input or external hardware and software failures? Is your code easy to maintain, particularly by future programmers who were not involved in its initial development? Are the components of the system modular? Can they be worked on, tested, and upgraded independently? Are the components of your system designed well enough to be reused for other applications? Are the elements of your system secure from malicious attacks? Finally, is it easy for the user to work with your software?
Each one of these questions is related to a separate sub-field in software engineering. It might be impossible to address them all completely, but different applications will have different priorities. One method for OO software engineering uses design patterns. The idea behind design patterns is that most classes share some common design principles with a large category of other classes. By naming and recognizing each category, you can apply the same rules to designing new classes from a category you’re already familiar with. Each category is called a design pattern. Java uses design patterns extensively in its API. Describing design patterns in greater depth is beyond the scope of this book, but you might want to consult the Gang of Four’s popular book Design Patterns.
Another important idea in design is design by contract. Although this is also a rich, complex area of software engineering, the idea can be applied to methods in a straightforward way. For each method, you have a formal explanation of what its input should be, what its output should be, and what else can be changed in the process. For some languages and some segments of code, it’s possible to prove that a given method does exactly what it’s supposed to do. Nevertheless, Donald Knuth, a giant in computer science, is famous for having said, "Beware of bugs in the above code; I have only proved it correct, not tried it."
16.6.2. Implementation
Once you have gotten your design to the implementation phase, there are a number of other techniques you can use to minimize errors. One interesting technique is pair programming, in which two programmers sit at a single computer and work together. Ideally, the programmer who is currently typing, often called the driver, is thinking about the immediate problems posed by the next few lines of code while the other programmer, often called the navigator, is thinking about the larger context of the program and watching for errors. Two sets of eyes are always beneficial when looking at something as detailed and confusing as a computer program.
In keeping with the theme of having more than one set of eyes looking at a program, it’s also useful to have the individuals who test the software be independent from those who develop it. By keeping the testers separate, they’re not infected by the assumptions and biases that the developers made while writing the software. Some communication between the two groups is necessary, but there’s value in black-box testing, which we’ll explain in the next subsection.
Another piece of general advice is to rely on standard libraries as much as possible. Reinventing your own libraries is partly a waste of time and partly dangerous because your own libraries haven’t undergone as much testing as the standard ones. Likewise, it makes your code less portable. Some expert developers might need to write special libraries for speed or memory efficiency, but they’re the exception, not the rule.
There are a number of Java specific implementation guidelines. People have written entire books about good software engineering in Java, and so we’ll only give a few obvious pointers.
Although it’s tempting to do so when working under time pressure, never
write empty exception handlers. Doing so swallows exceptions blindly,
giving the user no information about the errors in his or her program. By
the same token, always make your exception handlers as narrow as
possible. Simply putting catch(Exception e) at the end of any
try-block has one of two possible outcomes: In one case your handler
is vague and the user is informed that a general error of some kind has
occurred. In the other your handler is more specific than it has a right
to be. You might have assumed that a file I/O error was likely to
occur and always report that failure. Instead, an
ArrayOutOfBoundsException could happen and be mistakenly reported as a
file I/O problem.
You should test the input to any public methods you write and throw a pre-determined exception if the input is invalid. Never use assertions to test input to public methods. In fact, you should never depend on assertions to catch errors since they must be turned on in the JVM to have effect. Assertions are great for debugging code before it’s released but have little or no value in the field.
16.6.3. Testing
Once you’ve designed and implemented your program (or ideally throughout the process of implementation), you should test it to see if it behaves as expected and required. The most common form of software testing done by students is a form of smoke test. A smoke test is a basic test of functionality. Such a test should simply run through the major features of a program and verify that they seem to work under ordinary circumstances. Often a student will barely finish the program before the deadline and be unable to perform anything but the most basic tests.
Smoke tests are useful because it’s pointless to test the finer details of a system that’s clearly broken, but the software engineering industry uses many other kinds of testing to ensure that a given piece of software meets its specification. We’ll briefly cover three broad areas of testing: black-box testing, white-box testing, and regression testing.
Black-box testing
Black-box testing assumes that the tester knows nothing about the internal mechanisms of the software he or she is testing. The software is viewed as a “black box” with inputs and outputs but otherwise unknown internals. The tester chooses some subset of the possible inputs and tests to see if the output matches the specification.
For simple programs with very little input, it might be possible to test all possible input values, but doing so is impractical for most programs. A short list of techniques for determining the appropriate set of input values for black-box testing follows.
- Equivalence Partitioning
-
The idea behind equivalence partitioning is that large ranges of data might be functionally equivalent from the point of view of causing errors. If a tester can run a test for one element from a range of data, then the entire range can be tested quickly. To perform this kind of testing, the tester must partition data into ranges that function differently. The partition created is usually not really a partition in the mathematical sense as the sub-domains are overlapping. For this reason equivalence partitioning is also referred to as subdomain testing.
For example, a program controlling the temperature of the water in an aquarium might have legal input ranges between 32 °F and 212 °F. However, if the program warms the water when it’s below 75 °F and cools it when it’s above 90 °F, then values below 0, values from 0 to 74, values from 75 to 90, values from 91 to 212, and values above 212 all constitute different partitions. - Boundary Value Analysis
-
Once inputs have been partitioned into equivalent ranges, testers can focus on values which are near the boundaries of those ranges. For example, an input containing a person’s age might be allowed to range between 0 and 150. The values -1, 0, 1, 149, 150, and 151 are good candidates for input from the perspective of boundary value analysis. As with equivalence partitioning, boundary value analysis is useful not only for the boundaries between valid and invalid data but also for the boundaries between any input ranges with different program behavior such as the boundaries separating the five ranges of values for the aquarium thermostat program described above.
- All-Pairs Testing
-
Most software bugs are triggered by a single piece of input. Some harder to discover bugs require two separate pieces of input to have specific values at the same time before they manifest. With each increase in the number of different inputs that must each have specific values at the same time to cause a bug, the bug becomes increasingly difficult to detect but also increasingly unlikely to exist. It might be possible to test all possible values for a given input but impossible to test all possible values for all inputs at the same time. All-pairs testing is a compromise between these two extremes that tests all possible pairs of inputs.
- Fuzz Testing
-
The concept behind fuzz testing is to use large amounts of invalid, unlikely, or random data as input to a program. Although this kind of testing is used only to test the reliability and robustness of a program receiving unexpected input, it has a number of advantages. One significant advantage of fuzz testing is that it’s quick and easy to design test cases. Another is that it makes no assumptions about the program behavior, catching errors that might never occur to a human being. If fuzz testing is automated, it can also be used for stress testing, in which the program’s ability to process a large amount of data quickly or while remaining responsive is tested.
White-box testing
The philosophy of white-box testing is the opposite of black-box testing. When using white-box testing techniques, the tester has access to program internals. The tester should employ techniques to test every possible path that execution can take through the code. Traversing a particular path of execution through a program is called exercising that path.
In order to exercise every possible path, it’s necessary to force each conditional statement to be true on some path and false on another. Some combinations of true and false might be impossible, but ignoring this fact, a program with n independent conditionals would require 2n runs to test them all. Because of the large number of possible execution paths, white-box testing generally tries to maximize coverage over metrics that are not quite so demanding.
Method coverage is the percentage of methods that are called by test cases at least once. Ideally, this number is 100%. Statement coverage is the percentage of statements that are executed by test cases. Again, this number should be as close to 100% as possible. Branch coverage is the percentage of conditionals that have been executed on both their true and false branches. Getting total coverage here is difficult, but good testing can come close.
As with black-box testing, equivalence partitioning and boundary value methods can be used to reduce the total number of test cases. Also, it’s important to test those parts of your programs reached only in error conditions in addition to normal operation.
Regression testing
Regression testing is a form of testing that’s not often necessary for student code, which is usually focused on small projects. The motivating idea behind regression testing is that, in the act of fixing a bug or adding a feature, existing code can be broken. Thus, even after a system has been thoroughly tested, small changes or additions require the entire system to be retested. As the size of a program grows, the chance of unintended consequences increases, along with the value of performing regression testing.
Regression testing can incorporate both black- and white-box testing. Doing regression testing could simply mean running all the existing tests over after every major change. At the very minimum, each time a test uncovers a bug, that test should be added to the test suite used after each build of the program. The use of regression testing also implies that regular testing is being done on your code. Regular testing gives developers the opportunity to track changes in other aspects of their program such as memory usage, running time, responsiveness, and other non-functional issues.
16.7. Syntax: Java testing tools
One open-source tool for testing Java is called JUnit. There are other testing tools for Java, and there’s a wide array of tools for testing software in virtually any language. We cover JUnit here because it’s widely accepted as a standard Java testing tool and because it’s open source.
16.7.1. JUnit testing
JUnit testing is used for unit testing Java. Unit testing is the process of testing separate software components that will eventually work together. By testing them individually, debugging can be done before interactions between different components make it more difficult to find the underlying bugs. After unit testing comes integration testing to test how the components work together. Finally, system testing is the testing of the complete, integrated system against its specifications.
Annotations
Our coverage of JUnit testing is based on JUnit 5. This version of JUnit has simple syntax for creating JUnit tests compared to JUnit 3 and earlier, but it also relies on annotations. An annotation is additional information written into Java code that affects how the compiler or run-time system treats the code. They are like comments, but they can affect code execution or compilation, usually indirectly. Applying an annotation to a method is called decorating. A class, a method, a variable, a package, or even an individual method parameter can be decorated.
There are several annotations built into Java. Here, we consider three: @Deprecated,
@Override, and @SuppressWarnings. If a method is decorated with
@Deprecated, it’s deprecated and included only for backward compatibility.
The compiler will give a warning if you call deprecated code such as the following.
@Deprecated
public void oldMethod() {
...
}Many methods in the extensive Java API are deprecated, like
Thread.suspend(), due to its inherent deadlock risk. As of Java 5 when
annotations were introduced, existing deprecated methods were decorated with
@Deprecated. Before that, the only way to know that a method was deprecated
was by reading the documentation. The @Override annotation marks a method that’s
overriding a parent class method, causing a compiler error if the method
isn’t correctly overriding some parent class method. The @SuppressWarnings
annotation allows certain warning messages to be suppressed, like using
deprecated code if you really have to.
Basic JUnit syntax
First of all, JUnit is not a part of the standard Java API. To use it, you should download the latest jar file from the JUnit site and add the path to that jar file to your class path. Because JUnit is so universal, Eclipse, IntelliJ, and many other IDEs provide a way to add the JUnit library to a project without the need to download the jar file separately.
To access the JUnit facilities in your code, you need the following import.
Note that this import is different from JUnit 4 and earlier versions which
used classes from the org.junit package.
import org.junit.jupiter.api.*;Then, you need to set up a testing class just like you would any other
class. The key difference is that each method in the testing class is
designed to test some functionality of a code component. For example,
let’s imagine that we want to test functionality within the Java
Math class such as the ceil(), pow(), and sin() methods.
To do so, we create a class called MathTest with three methods inside
of it called ceilTest(), powTest(), and sinTest(). Note that it’s a
common JUnit convention to end the names of the testing methods with “Test.”
We’ll use each method to test the functionality of the three methods
that, respectively, have matching names. Although ending with “Test” is
a convention, there’s no requirement to name these methods any particular
way. Tests in JUnit don’t have to test single method calls. They could
test any functional aspect of an object or class. Nevertheless, for
documentation reasons it’s wise to give the test methods names that
reflect what’s being tested.
Where do annotations come in? The header for the ceilTest() method
should be as follows.
@Test
public void ceilTest()The only thing necessary to use a method for a JUnit test is to annotate
it with @Test. It’s also necessary to make any function used for
testing public with a void return type and no parameters. Otherwise,
the JUnit framework will crash when you try to run the tests. Each
method with a @Test annotation is run once by JUnit, but JUnit can’t
supply any arguments to them. They should be self-contained tests
without any outside input.
The exception to this rule is that you can perform some set up for the
tests and then some clean up afterward. Any method decorated with
@BeforeEach will be run before every test, and any method decorated with
@AfterEach will be run after every test. If you have some set up or
clean up that’s expensive to run, you can use the annotations
@BeforeAll or @AfterAll to decorate a static method that’s run
once before or after all the tests.
So far we have talked about the major aspects of writing a JUnit test class except for the test itself. How does the JUnit test report a success or a failure to the tester? As you would expect in Java, we use the exception handling mechanism to indicate failures. If the test method returns normally, the test is considered a success. If an unhandled exception or error is thrown by the method, the test is considered a failure. One of the most common ways of implementing this is by using a form of assertions.
Of course, you could simply add an assert into the test code, then
enable assertions while running the test, but this approach means that
your tests could all incorrectly pass if you forget to enable
assertions. Instead, use the following import.
import static org.junit.jupiter.api.Assertions.*;With this static import, you’ll have access to many static methods
that provide useful assertion functionality. The simplest of these is
assertTrue(), which is essentially equivalent to an assert without
requiring assertions to be enabled. For example, we could code the body
of the ceilTest() method as follows.
@Test
public void ceilTest() {
assertTrue(4 == Math.ceil(3.1));
}Another useful method is assertEquals() (and its close cousin
assertArrayEquals()) which takes two parameters and throws an
AssertionError if the two aren’t equal. There are overloaded versions
of this method for other primitive types and Object. Note that the preferred
assertEquals() method for the double type takes three parameters,
including a delta threshold in case the values don’t match exactly.
Using these methods, we can finally write a complete (though simple)
implementation of MathTest.java.
import org.junit.jupiter.api.*;
import static org.junit.jupiter.api.Assertions.*;
public class MathTest {
private static double sqrt2;
private static final double THRESHOLD = 0.000001;
@BeforeAll
public static void setUp() { sqrt2 = Math.sqrt(2);}
@Test
public void ceilTest() {
assertTrue(4 == Math.ceil(3.1));
}
@Test
public void powTest() {
assertEquals(2, Math.pow(sqrt2, 2), THRESHOLD);
}
@Test
public void sinTest() {
assertEquals(sqrt2/2.0, Math.sin(Math.PI / 4.0), THRESHOLD);
}
}Note that the setUp() method is extremely trivial here, and no clean
up is needed.
JUnit has many other powerful features that allow you to run suites of tests or repeated tests with specific parameterized values, but we’re only going to introduce one more feature here. In an ideal world, you develop tests as you develop code. In fact, a popular software development methodology is called test-driven development (TDD). The central idea behind TDD is writing your tests before you write your code. Doing so provides clarity about what you want your code to do, a way to know that you’ve written your code correctly, a way to document your code, and a suite of tests that grows along with your program.
Whether doing TDD or not, you might have completed a test for a specific
feature before you’ve finished implementing it. Or perhaps a feature
in your program is broken at the moment, but you want to continue
running tests on the rest of the features. In these cases and others, it’s
useful to turn off a particular test temporarily. To do this, you add the
annotation @Disabled before the @Test annotation. In parentheses after the
@Disabled annotation, you should ideally put in parentheses a String giving
the reason why the test is being disabled. There are even annotations that
allow you to run tests or disable them for particular platforms.
Running JUnit
Once you’ve created your JUnit test classes, you’ll want to run
them. There are tools built into IDEs like Eclipse to make running easier,
but the command line is always an option. As we said before, you need to
include the JUnit jar file in your classpath. You can either do this
permanently, by adding it to a CLASSPATH environment variable in a way
dependent on your OS, or for a particular run of a Java tool. Assuming
that you haven’t added the jar file to your classpath permanently, let’s
say that you’re using the JUnit Platform 1.5.1 that’s included with JUnit
5.5.1 from a jar file called junit-platform-console-standalone-1.5.1.jar
that can be found in C:\Java\JUnit\. If MathTest.java is in the current
directory, you would type the following.
javac -classpath .;C:\Java\JUnit\junit-platform-console-standalone-1.5.1.jar MathTest.java
To actually run the tests, you need to tell the platform where to
look for tests to run. Thus, you run the platform from its jar file, specifying that the class
path is the current directory (.), and then scan that directory for tests. Note that it’s
unnecessary to mention MathTest at this point since all tests in the specified class path will
be run.
java -jar C:\Java\JUnit\junit-platform-console-standalone-1.5.1.jar --class-path . --scan-class-path
The output should include something like the following, showing that all three tests passed.
╷ ├─ JUnit Jupiter ✔ │ └─ MathTest ✔ │ ├─ ceilTest() ✔ │ ├─ powTest() ✔ │ └─ sinTest() ✔ └─ JUnit Vintage ✔
For the command line, this output is impressive, yet the commands listed above to run JUnit are complex. These commands have many additional options, allowing you to include or exclude additional paths, directories, and file names. While it’s possible to run JUnit commands from the command line, the process is smoother through an IDE.
16.8. Concurrency: Testing tools
In this section, we describe some tools that exist specifically to help catch those bugs that crop up as a direct result of concurrency. This section is short, and that shortness reflects the fewness of good tools available. The design of concurrent debugging and testing tools is still an open research topic. The heart of the problem is that the nondeterminism present in concurrency makes bugs difficult to pin down. You could run a JUnit test 1,000,000 times and never see a peculiar race condition. From a brute force perspective, we could try to test all possible interleavings of thread execution, but this approach is not practical for large programs because the number of interleavings grows exponentially. Nevertheless, some research has focused on attacking the problem from this direction.
16.8.1. IBM ConTest
One tool that used this idea was ConTest from IBM. Normal JVM
operation makes some interleavings more likely than others. If the
correct output is very likely and the incorrect is very unlikely, it’s
easy for a tester to believe that the program works correctly. ConTest was a
tool that instrumented class files after they’d been compiled by
Java. When it instrumented these files, it added extra method calls into
concurrent code designed to introduce some randomness into the system.
By introducing sleep() and yield() methods in random places, the JVM
could be forced into producing interleavings that would otherwise be
unusual. The designers of ConTest used heuristics so that ConTest
added this randomness in “smart” locations designed to maximize unusual
interleavings and catch bugs.
ConTest was not a panacea. Although it revealed bugs that were rare, it still had to be combined with strong testing methodologies so that those bugs could be caught when they appeared. Another difficulty with using ConTest was that it couldn’t tell you where the problem happened or when it was likely to happen under normal circumstances. You were still dependent on your test design to reveal the source of the problem. ConTest also didn’t guarantee every possible ordering. Very rare bugs might not have manifested even after thousands of runs with ConTest instrumented code. Although ConTest was one of the most promising tools taking this approach, it is no longer available.
16.8.2. Devexperts tools
The open-source Lin-check framework has some similarities to ConTest. It was designed by Devexperts specifically to test data structures such as those we will discuss in Chapter 18. Like ConTest, Lin-check executes tests in parallel many times in an effort to find a concurrent interleaving that causes an error condition.
The Dl-check tool was also designed by Devexperts. Its goal is to find deadlocks that could happen in concurrent programs.
16.8.3. ConcJUnit and ConcurrentUnit
We hope we’ve convinced you of the value of using JUnit testing to unit test your programs. Of course, JUnit has limitations, especially when testing concurrent programs. JUnit uses exceptions to report failed test cases, but JUnit only reports exceptions from the main thread, not from any child threads that might be spawned. ConcJUnit allows exceptions thrown by child threads to be reported and also forces all child threads to join with the main thread.
In this way, it will be clear if any errors happened while a child thread was being executed, either causing an exception to be thrown or causing a child thread to fail to rejoin the main thread. ConcJUnit is intended as a drop-in replacement for JUnit, but only for JUnit 3 and 4. ConcJUnit is no longer under active development and is unlikely to have a version compatible with JUnit 5. ConcJUnit is part of a larger suite of open-source tools called Concutest maintained at the Concutest site.
ConcurrentUnit is another testing framework with annotations similar to those found in JUnit. Although it’s not intended as a replacement for JUnit, it has facilities like ConcJUnit that allow testers to discover when an exception occurs on child threads.
16.8.4. SpotBugs
SpotBugs (previously called FindBugs), is a static analysis tool that examines programs for a long list of errors. SpotBugs looks for patterns that match known errors. Most of the errors that SpotBugs looks for have nothing to do with concurrency, but a whole section of its bug list is devoted to multithreaded correctness. SpotBugs can help you find incorrect usage of synchronization tools as well as unsafe concurrent library usage.
16.8.5. Intel® tools
There are industry tools for debugging and optimizing threaded programs outside of Java. Intel® produces software such as the Intel® Inspector to find concurrent errors as well as the Intel® Vtune™ Amplifier to help tune threaded programs. These products from Intel®, like many concurrency tools, are focused on C/C++ and Fortran platforms. Historically, concurrency has been centered in the high performance and scientific computing markets. Java, in contrast, has been perceived as a slow language, better suited to desktop applications. As the role of concurrency continues to evolve, so will the tools to help programmers.
16.9. Examples: Testing a class
The larger the system, the more critical testing becomes. We don’t have the space to explain a complex testing example, but we can provide another example of JUnit testing.
Using an example from physics, we can create a PointCharge class that has
a certain charge and a specific location in 3D space. We’re also going to
introduce some errors into the class. Because the class is so simple, the
errors should be obvious. Nevertheless, we’ve picked reasonable errors that
might come up in real development.
public class PointCharge {
private double charge; // C
private double x; // m
private double y; // m
private double z; // m
public static final double K = 8.9875517873681764e9; // N m^2 C^-2
public PointCharge(double charge, double x, double y, double z) { (1)
this.charge = charge;
this.x = x;
this.y = y;
this.z = y;
}
public double getCharge() { return charge; }
public double distance(PointCharge p) { (2)
return distance(p.x, p.y, p.z);
}
private double distance(double x, double y, double z) { (3)
double deltaX = this.x - x;
double deltaY = this.y - y;
double deltaZ = this.z - z;
return Math.sqrt(deltaX*deltaX + deltaY*deltaY + deltaZ*deltaZ);
}
public double scalarForce(PointCharge p) { (4)
double r = distance(p);
return K*charge*p.charge/r*r;
}
public double fieldMagnitude(double x, double y, double z) { (5)
double r = distance(x, y, z);
return charge/(r*r);
}
}| 1 | The PointCharge class has a straightforward constructor followed by an
accessor. |
| 2 | Then, it has a method to determine distance to another PointCharge. |
| 3 | This method in turn relies on a private helper method that can compute distance from an arbitrary x, y, and z location. |
| 4 | Some of the harder work done by the class can be found in a method to determine the scalar force between two charges. |
| 5 | Another method finds the magnitude of the electric field due to the charge at some location. |
Recall from physics that the force F between two charges q1 and q2 is given by the following equation.

In this equation, ke is the proportionality constant 8.9875517873681764 × 109 N·m2·C-2 and r is the distance between the charges. Likewise, the electric field E at a given location due to a charge q is given below.

Let’s come up with a test for the distance() methods first. We’re
going to need some other PointCharge objects. Let’s make four altogether:
one at the origin and three one meter along each positive axis. We can create
these charges in a set up method. While we’re at it, we’ll give them a
variety of positive and negative charges.
@BeforeEach
public void setUp() {
charge1 = new PointCharge(1, 0, 0, 0);
charge2 = new PointCharge(2, 1, 0, 0);
charge3 = new PointCharge(-1, 0, 1, 0);
charge4 = new PointCharge(0, 0, 0, 1);
}To test the distance() method thoroughly, we’ll check the distance
from charge1 to all the other charges as well as charge2 to
charge3.
@Test
public void distance() {
assertEquals(1.0, charge1.distance(charge2), 0.000001);
assertEquals(1.0, charge1.distance(charge3), 0.000001);
assertEquals(1.0, charge1.distance(charge4), 0.000001);
assertEquals(Math.sqrt(2.0), charge2.distance(charge3), 0.000001);
}The distances between charge1 and the other three should be 1, and the
distance between charge2 and charge3 should be around the square root of two.
Yet when we run this test with JUnit, the test
fails with the following error.
java.lang.AssertionError: expected:<1.0> but was:<1.4142135623730951>
This error happens on the second assertion in the method. But why? If we comb through the
distance() methods in PointCharge, they all look correct. The
problem must be deeper. PointCharge doesn’t have accessor methods for
its location, so we can’t test those. Checking the constructor, we
find the culprit: this.z = y;, a simple cut and paste error.
With the distance() methods working, we can run a similar test for
scalarForce() generated by plugging in appropriate values into the
equation for F.
@Test
public void scalarForce() {
assertEquals(2*PointCharge.K, charge1.scalarForce(charge2), 0.000001);
assertEquals(-PointCharge.K, charge1.scalarForce(charge3), 0.000001);
assertEquals(0.0, charge1.scalarForce(charge4), 0.000001);
assertEquals(-PointCharge.K, charge2.scalarForce(charge3), 0.000001);
}When we run this test with JUnit, the last assertion fails. We get the following output.
java.lang.AssertionError: expected:<-8.987551787368176E9> but was:<-1.797510357473635E10>
A close inspection reveals that the actual value is about twice the
expected value. Where does this extra factor of 2 come from? Scanning
the code for scalarForce(), we find return K*charge*p.charge/r*r;
We forgot parentheses and messed up our equation. What we really wanted
was return K*charge*p.charge/(r*r);
The most striking thing about this example is that three test cases passed! Perhaps that means that we were choosing values that were too simple, but it also illustrates the importance of thorough testing.
Finally, let’s test the value of the fieldMagnitude() method. For
simplicity, we’ll test the field at the locations of charge1,
charge3, and charge4 with respect to charge2.
This time the first assertion fails. We get the following output.
java.lang.AssertionError: expected:<1.797510357473635E10> but was:<2.0>
2.0 seems like a very strange result when we were expecting a value
with an order of magnitude 10 times larger. Perhaps a constant was
omitted? Yes, our version of fieldMagnitude() left off a factor of
K. Once we fix that, our code finally passes all three tests. Why didn’t
we fail the assertions after the first one? Because of the exception handling
mechanism, each JUnit test method stops once a failure has happened.
Here is the fully corrected version of PointCharge renamed
FixedPointCharge.
PointCharge.public class FixedPointCharge {
private double charge; // C
private double x; // m
private double y; // m
private double z; // m
public static final double K = 8.9875517873681764e9; // N m^2 C^-2
public FixedPointCharge(double charge, double x, double y, double z) {
this.charge = charge;
this.x = x;
this.y = y;
this.z = z;
}
public double getCharge() { return charge; }
public double distance(FixedPointCharge p) {
return distance(p.x, p.y, p.z);
}
private double distance(double x, double y, double z) {
double deltaX = this.x - x;
double deltaY = this.y - y;
double deltaZ = this.z - z;
return Math.sqrt(deltaX*deltaX + deltaY*deltaY + deltaZ*deltaZ);
}
public double scalarForce(FixedPointCharge p) {
double r = distance(p);
return K*charge*p.charge/(r*r);
}
public double fieldMagnitude(double x, double y, double z) {
double r = distance(x, y, z);
return K*charge/(r*r);
}
}And, for easy readability, here’s the full JUnit test class
TestPointCharge. Note that you will have to change the name
PointCharge to FixedPointCharge if you want to test the corrected
class.
PointCharge.import org.junit.jupiter.api.*;
import static org.junit.jupiter.api.Assertions.*;
public class TestPointCharge {
private PointCharge charge1;
private PointCharge charge2;
private PointCharge charge3;
private PointCharge charge4;
@BeforeEach
public void setUp() {
charge1 = new PointCharge(1, 0, 0, 0);
charge2 = new PointCharge(2, 1, 0, 0);
charge3 = new PointCharge(-1, 0, 1, 0);
charge4 = new PointCharge(0, 0, 0, 1);
}
@Test
public void distanceTest() {
assertEquals(1.0, charge1.distance(charge2), 0.000001);
assertEquals(1.0, charge1.distance(charge3), 0.000001);
assertEquals(1.0, charge1.distance(charge4), 0.000001);
assertEquals(Math.sqrt(2.0), charge2.distance(charge3), 0.000001);
}
@Test
public void scalarForceTest() {
assertEquals(2*PointCharge.K, charge1.scalarForce(charge2), 0.000001);
assertEquals(-PointCharge.K, charge1.scalarForce(charge3), 0.000001);
assertEquals(0.0, charge1.scalarForce(charge4), 0.000001);
assertEquals((double)-PointCharge.K, (double)charge2.scalarForce(charge3), 0.000001);
}
@Test
public void fieldMagnitudeTest() {
assertEquals(2*PointCharge.K, charge2.fieldMagnitude(0, 0, 0), 0.000001);
assertEquals(PointCharge.K, charge2.fieldMagnitude(0, 1, 0), 0.000001);
assertEquals(PointCharge.K, charge2.fieldMagnitude(0, 0, 1), 0.000001);
}
}16.10. Exercises
Conceptual Problems
-
What’s the purpose of the
assertkeyword in Java? What steps must be taken for it to be active? -
What’s the value of
jafter the following statements are executed?int j = 1; int i; for(i = 0; i < 10; i++); j += i;Assuming the programmer made an error, what category of programming error does it fall under?
-
The following loop is intended to print out all possible
bytevalues. What’s the conceptual error made in the following loop? How many times will it execute?for(byte value = 0; value < 256; ++value) System.out.println("Byte: " + value); -
What are all the possible run-time errors that could occur in this method that reverses a section of an array?
public void reverse(Object[] array, int start, int end) { Object temp; end--; // Up to but not including end while(start < end) { temp = array[start]; array[start] = array[end]; array[end] = temp; start++; end--; } }What checks could be added to catch these errors?
-
Recall the idea of a stack mentioned in Section 9.1. Consider the following definition of a stack designed to hold
intvalues.public class IntegerStack { private static Node { public int data; public Node next; } private Node head = null; public void push(int value) { Node temp = new Node(); temp.data = value; temp.next = head; head = temp; } public void pop() { head = head.next; } public int top() { return head.data; } public boolean isEmpty() { return head == null; } }What exceptions could be thrown when using this class? Where could they be thrown?
-
Imagine that you have a simple linked list such as the ones described in Section 18.2.2. What if there’s a loop in the list such that the last element in the list points to an earlier element in the list? For this reason, a simple traversal of the list will go on forever. How could you detect such a problem during program execution? Note that this question sometimes comes up in job interviews.
-
What’s the difference between black-box testing and white-box testing? What kinds of bugs are more likely to be caught by black-box testing? By white-box testing?
-
The Microsoft Zune was a portable media player in competition with the Apple iPod. The first generation Zune 30 received negative publicity because many of them froze on December 31, 2008 due to a leap year bug. It’s possible to find segments of the source code that caused this problem on the Internet. Essentially, the clock code for the Zune behaved correctly on any day of the year numbered 365 or lower. Likewise, when the day was greater than 366, it would correctly move to the next year and reset the day counter. When day was exactly 366, however, the Zune became stuck in an infinite loop. What kind of testing should Microsoft have done to prevent this bug?
Programming Practice
-
Apply JUnit testing to the last major assignment you did in class. What bugs did you uncover?
Experiments
-
James Gosling’s original specification for Java contained assertions, but they weren’t included until Java 1.4. One of the concerns about an assertion mechanism is the additional time required to process the assertions. Time a program of at least moderate length before adding
assertstatements to its methods. If you useassertstatements to check method input and output thoroughly, you should see a slight decrease in performance when assertions are enabled. When disabled, you should see almost none. How great is the performance hit? -
Take another look at your last programming assignment. Calculate the number of branches based on
ifandswitchstatements and compute 2 raised to that power. Time your program executing once under normal circumstances. Multiply that time by the number of different possibilities you would need to exercise every possible combination of branches in your program. How much total time would it take to run all of those different executions of your program? -
Take a concurrent program you’ve written that relies on explicit synchronization mechanisms for correctness. Remove all synchronization tools and run the code many times, testing for race conditions. How many runs does it take before a race condition causes an error? If you can, run your program on systems with different numbers of cores. Using a larger number of cores should make race conditions more evident since more processors can execute contentious code in parallel.
17. Polymorphism
…how strange it is to be anything at all.
17.1. Problem: Banking account with a vengeance
In Chapter 14, we introduced the
SynchronizedAccount class that guarantees that checking the balance,
making deposits, and making withdrawals will all be safe even in a
multi-threaded environment. Unfortunately, SynchronizedAccount provides
few of the options a full bank account should have. The problem we
present to you now is to create an entire line of bank accounts which
all inherit from SynchronizedAccount. Because of inheritance, all
accounts will at least have getBalance(), deposit(), and
withdraw() methods.
You must create three new account classes. The constructor for each
class must take a String which gives the name of the person opening
the account and a double which gives the starting balance of the
account. The first of these classes is CheckingAccount. The rules for
the checking account implemented by this class are simply that the
customer is charged $10 every month that the account is open. The second
class is DirectDepositAccount. This account is very similar to the
basic checking account except that an additional method
directDeposit() has been added. On its own, directDeposit() appears
to operate like deposit(); however, if a direct deposit has been made
in the last month, no service fee will be charged to the account.
The SavingsAccount class operates somewhat differently. In addition to
a name and a starting balance, the constructor for a SavingsAccount
takes a double which gives the annual interest rate the account earns.
Each month the balance is checked. If the balance of the account is
greater than $0, the account earns interest corresponding to
1/12 of the annual rate. However, if the balance
is below $1,000, a $25 service fee is charged each month, regardless of
how low the balance becomes.
In Chapter 11 you were exposed to concepts surrounding inheritance in object-oriented programming. We now return to these concepts and explore them further. In the first place, concurrency is on the table now, and you must be careful to keep your derived classes thread safe. In the second, we’ll discuss the full breadth of inheritance. The tools we describe here are intended to allow you to solve this extended bank account problem (and indeed many other problems) with as little code as possible.
17.2. Concepts: Polymorphism
Perhaps the most important reason for inheritance is code reuse. When you
can successfully reuse existing code, you’re not just saving the time
of writing new code. You’re also leveraging the quality and correctness
of the existing code. For example, when you create your own class which
extends Thread, you’re confident that all the thread mechanisms work
properly.
You can reuse code by taking a class that does something you like, say
the Racecar class, and enhance it in some way, perhaps so that it
becomes the TurboRacecar class. If you use the TurboRacecar class on
its own, your code reuse is through simple inheritance. If you use
TurboRacecar objects with a RaceTrack class, which was written to
take Racecar objects as input, you’ve entered the realm of
polymorphism. Polymorphism means that the same method can be used on
different types of objects without being rewritten. In Java,
polymorphism works by allowing the programmer to use a child class in
any place where a parent class could have been used.
17.2.1. The is-a relationship
Consider the two following class definitions.
public class Racecar {
public double getTopSpeed() { return 200.0; }
public int getHorsepower() { return 700; }
public double speed = 0;
}public class TurboRacecar extends Racecar {
public int getHorsepower() { return 1100; }
}Now, imagine that a RaceTrack has an addCar(Racecar car) method
which adds a Racecar to the list of cars on the track. When the cars
begin racing, the RaceTrack object will query the cars to see how much
horsepower they have. A Racecar object will return 700 when
getHorsepower() is called, but a TurboRacecar will return 1100.
Even through the TurboRacecar doesn’t have an explicit
getTopSpeed() method, it inherits one from Racecar. Like all derived
classes in Java, TurboRacecar has all the methods and fields that
Racecar does. This relationship is called an is-a relationship
because every TurboRacecar is a Racecar in the sense that you can
use a TurboRacecar whenever a Racecar is required.
17.2.2. Dynamic binding
There’s a little bit of magic that makes polymorphism work. When you
compile your code, the RaceTrack doesn’t know which getHorsePower()
method will eventually get called. Only at run time does it query the
object in question and, if it’s a TurboRacecar, use the overridden
method that returns 1100. This feature of Java is called dynamic
binding. Not every object oriented programming language supports
dynamic binding. C++ actually allows the programmer to specify whether
or not a method is dynamically bound.
Only methods are dynamically bound in Java. Fields are statically
bound. Consider the following re-definitions of Racecar and
TurboRacecar.
public class StaticRacecar {
public static final double TOP_SPEED = 200.0;
public static final int HORSEPOWER = 700;
public double speed = 0;
}public class StaticTurboRacecar extends StaticRacecar {
public static final int HORSEPOWER = 1100;
}Assume that RaceTrack contains a method which prints out the
horsepower of a StaticRacecar like so:
public void printHorsepower(StaticRacecar car) {
System.out.print(car.HORSEPOWER);
}Even if you pass an object of type StaticTurboRacecar to the
printHorsepower() method, the value 700 will be printed out every time.
In Java, all fields, whether normal, static, or final are statically bound,
meaning that the variable type determines which field will be used at compile
time. In contrast, dynamic binding means that the true type of the object
(not the reference variable pointing to it) determines the method that will be
called at run time. Dynamic binding applies only to regular instance methods.
As their name implies, static methods are statically bound, determined at
compile time by reference type.
17.2.3. General vs. specific
Another way to look at inheritance is as a statement of specialization
and generalization. A TurboRacecar is a specific kind of Racecar
while Racecar is a general category that TurboRacecar belongs to.
The rules of Java say that you can always use a more specific version of
a class than you need but never a more general one. You can use a
TurboRacecar any time you need a Racecar but never use a Racecar when
you need a TurboRacecar. A square will do the job of a rectangle, but a
rectangle will not always be suitable when a square is needed.
Consider the following two classes:
public class Vehicle {
public void travel(String destination) {
System.out.println("Traveling to " + destination + "!");
}
}public class RocketShip extends Vehicle {
public void blastOff() {
System.out.println("10, 9, 8, 7, 6, 5, 4, 3, 2, 1 *ROAR*");
}
}Here’s a method that requires a RocketShip but only uses its
travel() method.
public void takeVacation(RocketShip ship, String destination) {
ship.travel(destination);
}It seems as though we should be able to pass any Vehicle to the
takeVacation() method because the only method in ship used by
takeVacation() is travel(). However, the programmer
specified that the parameter should be a RocketShip, and Java plays it
safe. Just because it looks like there won’t be a problem, Java isn’t
going to take any chances on passing an overly general Vehicle when a
RocketShip is required. If Java took chances, a problem could arise if
the takeVacation() method was overridden by a method that did call
ship.blastOff().
In summary, you can pass a RocketShip to a method which takes a
Vehicle or store a RocketShip into an array of Vehicles, but not the
reverse. Java usually gives a compile time error if you try to put
something too general into a location that’s too specific, but there are some
situations which are so tricky that Java doesn’t catch the
error until run time. Arrays, specifically, can cause problems. Examine
the following code snippet.
Vehicle[] transportation = new RocketShip[100];
transportation[0] = new Vehicle();On the first line, we’re using a Vehicle array reference to store an
array of 100 RocketShip references. But, in the second line, we try to store a
Vehicle into an array that’s really a RocketShip array, even though
it looks to the compiler like a Vehicle array. Doing so will compile
but throw an ArrayStoreException at run time.
17.3. Syntax: Inheritance tools in Java
So far, we’ve described polymorphism in Java with a conceptual focus.
In our previous examples, the only language tool needed to use
polymorphism was the extends keyword which you’re now well familiar with.
There are a number of other tools designed to help you structure
class hierarchies and enforce design decisions.
17.3.1. Abstract classes and methods
One such tool is abstract classes. An abstract class is one which can
never be instantiated. In order to use an abstract class, it’s
necessary to make a child class from it. To create an abstract class, you
simply add the abstract keyword to its definition, as in the
following example.
public abstract class Useless {
protected int variable;
public Useless(int input) {
variable = input;
}
public void print() {
System.out.println(variable);
}
}This class is useless for a number of reasons. For one thing, there’s no
way to find out the value of variable except by printing it out.
Furthermore, there’s no way to change the value of variable after the
object’s been created. Finally, since an abstract class can’t be
instantiated, the following code snippet will not compile.
Useless thing = new Useless(14);Instead, we must create a new class that extends Useless.
public class Useful extends Useless {
public Useful(int value) {
super(value);
}
public int getVariable() { return variable; }
public void setVariable(int value) {
variable = value;
}
}Then, we can instantiate an object of type Useful and use it for
something.
Useless item = new Useful(14);
item.print();Note that, in accordance with the rules of Java, we can store an object
with the more specific type Useful into a reference with the more general
type Useless. Even though Java knows that the object it points to will
never actually be a Useless object, it’s perfectly legal to have a
Useless reference. You can use abstract classes in this way to provide
a base class with some fundamental fields and methods that all other
classes in a particular hierarchy need. By using the keyword abstract,
you’re marking the class as template for other classes instead of as a
class that will be used directly.
Methods can be abstract as well. If you have an abstract class, you can create a method header which describes a method that all non-abstract children classes must implement, as shown below.
public abstract class Sequence {
protected int number;
protected final int CONSTANT;
public Sequence(int number, int constant) {
this.number = number;
CONSTANT = constant;
}
public abstract int getNextValue();
}This abstract class is supposed to be a template for classes which can
produce some sequence of numbers. Note that there’s no body for the
getNextValue() method. It simply ends with a semicolon. Every
non-abstract derived class must implement a getNextValue() method to
produce the next number in the sequence. For example, we could implement
an arithmetic or a geometric sequence as follows.
public class ArithmeticSequence extends Sequence {
public ArithmeticSequence(int firstTerm, int difference) {
super(firstTerm, difference);
}
public int getNextValue() {
number += CONSTANT;
return number;
}
}public class GeometricSequence extends Sequence {
public GeometricSequence(int firstTerm, int ratio) {
super(firstTerm, ratio);
}
public int getNextValue() {
number *= CONSTANT;
return number;
}
}The Sequence class doesn’t specify how the sequence of numbers
should be generated, but any derived class must implement the
getNextValue() method in order to compile. By using an abstract class,
we don’t have to create a base class which generates a meaningless
sequence of numbers just for the sake of establishing the
getNextValue() method. Abstract classes are like interfaces in that they
can force the programmer who’s extending them to implement particular methods,
but unlike interfaces they can also define fields and methods of any kind.
Here’s a more involved example of an abstract class that gives a first step toward solving the bank account with a vengeance problem posed at the beginning of the chapter.
import java.util.Calendar; (1)
public abstract class BankAccount extends SynchronizedAccount { (2)
private String name;
private Calendar lastAccess;
private int monthsPassed = 0;| 1 | The first step is to import the Calendar class for some date tools
we’re going to use later. |
| 2 | We extend SynchronizedAccount and declare the new class to be
abstract. In this example, we don’t use any abstract methods, but
since each bank account has unique characteristics, we don’t want people
to be able to create a generic BankAccount. |
public BankAccount(String name, double balance) throws InterruptedException {
this.name = name;
changeBalance(balance);
lastAccess = Calendar.getInstance();
}
public String getName() { return name; }
protected Calendar getLastAccess() { return lastAccess; }
protected int getMonthsPassed() { return monthsPassed; }The constructor and the accessors should be what you expect to see. Note
that calling the static method Calendar.getInstance() is the correct
way to get a Calendar object with the current date and time.
public final double getBalance() throws InterruptedException {
update();
return super.getBalance();
}
public final void deposit(double amount) throws InterruptedException {
update();
super.deposit(amount);
}
public final boolean withdraw(double amount) throws InterruptedException {
update();
return super.withdraw(amount);
}Then come the balance checking and changing methods. Each calls its parent
method after calling an update() method we discuss below.
protected synchronized void update() throws InterruptedException {
Calendar current = Calendar.getInstance();
int months = 12*(current.get(Calendar.YEAR) -
lastAccess.get(Calendar.YEAR)) + (current.get(Calendar.MONTH) -
lastAccess.get(Calendar.MONTH));
if(months > 0) {
lastAccess = current;
monthsPassed = months;
}
}
} Other than adding String for a name associated with the account, the
update() method is the other major addition made in BankAccount.
Each time update() is called, the number of months since the last
access is stored in the field monthsPast and the timestamp of the last
access is stored in lastAccess. We didn’t need these time features
before, but issues like earning interest or paying monthly service
charges will make them necessary. This method is synchronized so that
the two fields associated with the last access are updated atomically.
17.3.2. Final classes and methods
If you look at the previous example carefully, you’ll notice that the
methods getBalance(), deposit(), and withdraw() were each declared
with the keyword final. You’ve seen this keyword used to declare
constants before. The meaning that final has for methods is similar to
what it means for constants (and almost the opposite of abstract). A method
which is declared final can’t be overridden by child classes. If you’re
designing a class hierarchy and you want to lock a method into doing a
specific thing and never changing, this is the way to do it.
Like abstract, the keyword final can be applied to a class as well.
If you want to prevent a class from being extended further, apply the
final keyword to its definition. You might not find yourself using this
feature of Java very often. It’s primarily useful in situations where a
large body of code has been designed to make use of a specific class.
Making child classes from that class could cause unexpected problems.
The most common example of a final class is the String class.
Consider the following.
public class SuperString extends String {}This code will give a compiler error. String is perfect the way it is
(or so the Java designers have decided). Use of the final keyword for
classes, methods, and especially to specify constants allows the compiler to do
performance optimizations that would otherwise be impossible.
17.3.3. Casting
Polymorphism gives us greater power and flexibility when writing code. For
example, we can make a Vehicle array and store child class objects of
Vehicle inside, like so.
Vehicle[] vehicles = new Vehicle[5];
vehicles[0] = new Skateboard();
vehicles[1] = new RocketShip();
vehicles[2] = new SteamBoat();
vehicles[3] = new Car();
vehicles[4] = new Skateboard;This process could be infinitely more complex. We could be reading data
out of a file and dynamically creating different kinds of Vehicle
objects, but the final product of an array of Vehicle objects is the
important thing. Now, we can run through the array with a loop and have
the code magically work for each kind of Vehicle.
for(int i = 0; i < vehicles.length; i++)
vehicles[i].travel("Prague");Each Vehicle will travel to Prague as it should. The only trouble is
that we’ve hidden some information from the compiler. We know that
vehicles[1] is a RocketShip, but we can’t treat it like one.
vehicles[1].blastOff();This code won’t compile.
RocketShip ship = vehicles[1];This code won’t compile either. In both cases, we must use an
explicit cast to tell the compiler that the object really is a
RocketShip.
((RocketShip)vehicles[1]).blastOff();
RocketShip ship = (RocketShip)vehicles[1];Now, both lines of code work. The compiler is always conservative. It never makes guesses about the type of something. Consider the following.
Vehicle ship = new RocketShip();
ship.blastOff();Even though ship must be a RocketShip, Java doesn’t assume that it is.
The compiler uses the reference type Vehicle to do the check and will
refuse to compile. Casting allows us to use our human insights to
overcome the shortsightedness of the compiler. Unfortunately, there’s no
guarantee that human insights are correct. What happens if you cast improperly?
Vehicle vehicle = new Skateboard();
RocketShip ship = (RocketShip)vehicle;
ship.blastOff();In this example, we’re trying to cast a Skateboard into a
RocketShip. At compile time, no errors will be found. Because we use
explicit casting, the compiler assumes that we, powerful human beings
that we are, know what we’re doing. The error will happen at run time
while executing the second line. Java will try to cast vehicle into a
RocketShip, fail, and throw a ClassCastException.
Java provides some additional tools to make casting easier. One of these
is the instanceof keyword which can be used to test if an object is an
instance of a particular class (or one of its derived classes). For
example, we can make an object execute a special command if we know that
the object is capable of it.
public void visitDenver(Vehicle vehicle) {
if(vehicle instanceof RocketShip)
((RocketShip)vehicle).blastOff();
vehicle.travel("Denver");
}Even inside this if statement where it must be the case that vehicle
is a RocketShip, we still must perform an explicit cast. Sometimes
instanceof is not precise enough. If you must be sure that the object
in question is a particular class and not just one of its child classes, you
can use the getClass() method on any object and compare it to the
static class object. Using this tool, we can rewrite the former example
to be more specific.
public void visitDenver(Vehicle vehicle) {
if(vehicle.getClass() == RocketShip.class)
((RocketShip)vehicle).blastOff();
vehicle.travel("Denver");
}This version of the code will only call blastOff() for objects of
class RocketShip and not for objects of a child class like
FusionPoweredRocketShip.
17.3.4. Inheritance and exceptions
Beyond ClassCastException, there are a few other issues that come up
when combining exceptions with inheritance. As you already know, an
exception handler for a parent class will work for a child class. As
such, when using multiple exception handlers, it’s necessary to order
them from most specific to most general in terms of class hierarchy.
However, there’s another subtle rule that’s necessary to keep
polymorphism functioning smoothly. Let’s consider a Fruit class with
an eat() method that throws an UnripeFruitException.
public class Fruit {
public void eat() throws UnripeFruitException {
...
}
}Almost any fruit can be unripe, and it can be unpleasant to try to eat such
a fruit. But there are other things that can go wrong when eating
fruit. Consider the Plum class derived from Fruit.
public class Plum extends Fruit {
public void eat() throws UnripeFruitException, ChokingOnPitException {
...
}
}In the Plum class, the eat() method has been overridden to tackle
the special ways that eating a plum is different from eating fruit in
general. When eating a plum, you can make a mistake and try to swallow
the pit, throwing, it seems, a ChokingOnPitException. This scenario
seems natural, but it’s not allowed in Java.
The principle behind polymorphism is that a more specialized version of
something can always be used in place of a more general version. Indeed,
if you use a Plum in place of a Fruit, calling the eat() method is no
problem. The problem only happens if a ChokingOnPitException is thrown.
Code that was designed for Fruit objects knows nothing about a
ChokingOnPitException, so there’s no way for such code to catch the
exception and deal with the situation.
There’s nothing wrong with throwing exceptions on overridden methods.
The rule is that the overriding method must throw a subset of the exceptions
that the overridden method throws. This subset doesn’t need to be a proper
subset, so it could be all, some, or none of the exceptions thrown by the
overridden method. This rule demonstrates a concept called Hoare’s rule of
consequence that pops up many times in programming language design. Essentially,
if you start with something that works, you can tighten the requirements on
the input (using a Plum instead of any Fruit) and loosen the requirements
on the output (throwing fewer exceptions than were originally thrown), and it
will still work.
Here we have a few additional examples in a somewhat larger class hierarchy.

public abstract class Animal {
private boolean alive = true;
private boolean happy = true;
private final boolean warmBlooded;
public Animal(boolean warmBlooded) {
this.warmBlooded = warmBlooded;
}
public boolean isHappy() { return happy; }
public void setHappy(boolean value) { happy = value; }
public boolean isAlive() { return alive; }
public void die() { alive = false; }
}We begin with the abstract Animal class. This class gives a base
definition for animals which includes whether the animal is alive,
whether the animal is happy, and whether it’s warm-blooded (declared
final because an animal can’t switch between warm-blooded and
cold-blooded).
public abstract class Mammal extends Animal {
public static final boolean MALE = false;
public static final boolean FEMALE = true;
private boolean gender;
public Mammal(boolean gender) {
super(true);
this.gender = gender;
}
public boolean getGender() { return gender; }
public abstract String makeSound();
}We then extend Animal into Mammal. All mammals are warm-blooded,
which is reflected in the constructor call to the base class. In
addition, it’s assumed that all mammals make some sound. Mammals generally
also have well-defined genders. Like Animal, Mammal is an abstract class,
and any non-abstract child of Mammal must implement makeSound().
public class Platypus extends Mammal {
public Platypus(boolean gender) {
super(gender);
}
public String makeSound() {
return "Quack!";
}
public Egg layEgg() {
if(getGender() == FEMALE)
return new Egg();
else
return null;
}
public void poison(Animal victim) {
if(getGender() == MALE)
victim.setHappy(false);
}
}The Platypus class extends Mammal and adds the unusual things that a
platypus can do: laying eggs (if female) and poisoning other animals (if
male).
public class Human extends Mammal {
public Human(boolean gender, boolean happy) {
super(gender);
setHappy(happy);
}
public String makeSound() {
return "Hello, world.";
}
}The Human class also extends Mammal. Depending on the problem being
solved, this class might warrant a great deal more specialization. Right
now the main addition is taking happiness as an argument to the
constructor since the default human state is not necessarily happiness.
public final class DavidBowie extends Human {
public DavidBowie() {
super(MALE, true);
}
public String makeSound() {
return "I always had a repulsive need to be something more than human.";
}
}Finally, the DavidBowie class extends Human and is declared a final
class because it’s impossible to add anything to David Bowie.
Our examples have stretched fairly long in this chapter. It’s difficult to give strong motivation for some aspects of inheritance and polymorphism without a large class hierarchy. These tools are designed to help organize large bodies of code and should become more useful as the size of the problem you’re working on grows. One of the best examples of the success of inheritance is the Java API itself. The standard Java library is large and depends on inheritance a great deal.
17.4. Solution: Banking account with a vengeance
Now, we return to the specific problem given at the beginning of the
chapter and give its solution. We’ve already given you the
BankAccount abstract class which provides a lot of structure.

BankAccount that models a normal checking account.public class CheckingAccount extends BankAccount {
public static final double FEE = 10;
public CheckingAccount(String name, double balance)
throws InterruptedException {
super(name, balance);
}
protected synchronized void update() throws InterruptedException {
super.update();
changeBalance(-getFee()*getMonthsPassed());
}
protected double getFee() { return FEE; }
}The most basic account is the CheckingAccount. As you recall from the
BankingAccount class, the getBalance(), deposit(), and
withdraw() methods are all declared final. At first it seems as if
there’s no way to change these methods to add the $10 service charge.
However, each of those methods calls the update() method first to take
care of any bookkeeping. By overriding the update() method, we can
easily add the service charge. The new update() method calls the
parent update() to calculate the passage of time, then it changes the
balance based on the number of months that have passed.
The system we’ve adopted may seem unusual at first. Any time the
balance is checked, deposited to, or withdrawn from, we call update().
By updating the account to reflect any months which may have passed
before continuing on, we don’t have to write code which periodically
updates each bank account. Each bank account is only updated if needed.
We were careful to mark update() as synchronized. Although the
chance of an error happening is small, we make the update of the
internal Calendar and the application of any fee atomic, just to be
safe.
Note that we don’t use the constant FEE directly in update().
Instead, we call the getFee() method. The reason for this decision is
due to the next class.
CheckingAccount that models the behavior of accounts with direct deposits.import java.util.Calendar;
public class DirectDepositAccount extends CheckingAccount {
protected Calendar lastDirectDeposit;
public DirectDepositAccount(String name, double balance)
throws InterruptedException {
super(name, balance);
lastDirectDeposit = Calendar.getInstance();
}
public double getFee() {
Calendar current = Calendar.getInstance();
int months = 12*(current.get(Calendar.YEAR) -
lastDirectDeposit.get(Calendar.YEAR)) +
(current.get(Calendar.MONTH) -
lastDirectDeposit.get(Calendar.MONTH));
if(months <= 1)
return 0;
else
return super.getFee();
}
public void directDeposit(double amount) throws InterruptedException {
deposit(amount);
lastDirectDeposit = Calendar.getInstance();
}
}The DirectDepositAccount class extends the CheckingAccount class.
Note that the update() method hasn’t been overridden. We’ve added
another Calendar object to keep track of the last time a direct
deposit was made. Then, we override the getFee() method. If there’s
been a recent direct deposit, the fee is nothing; otherwise, it
returns the fee from the CheckingAccount. Because of dynamic binding,
the update() method defined in CheckingAccount will call this
overridden getFee() method for DirectDepositAccount objects.
BankAccount that models the behavior of a savings account.public class SavingsAccount extends BankAccount {
public static final double MINIMUM = 1000;
public static final double FEE = 25;
protected final double RATE;
public SavingsAccount(String name, double balance, double rate)
throws InterruptedException {
super(name, balance);
RATE = rate;
}
protected double getFee() { return FEE; }
protected double getMinimum() { return MINIMUM; }
protected synchronized void update() throws InterruptedException {
super.update();
int months = getMonthsPassed();
for(int i = 0; i < months; i++) {
if(getBalance() > 0)
changeBalance(getBalance() * (1 + RATE/12));
if(getBalance() < getMinimum())
changeBalance(-getFee());
}
}
}There should be few surprises in the last class, SavingsAccount. The
biggest difference is that we use a loop in the update() method to
update the balance because the account could be gaining interest and
also incurring fees. The interaction of the two operations might give a
different result than applying each in a block for the backlog of
months.
This set of classes might not resemble the way a real, commercial-grade banking application works. Nevertheless, with inheritance and polymorphism we were able to create bank accounts which do some complicated tasks with a relatively small amount of code. At the same time, we preserved thread safety so that these accounts can be used in concurrent environments.
17.5. Concurrency: Atomic libraries
This chapter has discussed using polymorphism to reuse code. To solve the banking account with a vengeance problem from the beginning of the chapter, we explored the process of extending several bank account classes to add additional features while working hard to maintain thread safety.
Code can be reused by extending classes with child classes or by using
instances of existing classes as fields. There’s no single solution
that’s best for every case. As in the bank account examples, it can be
difficult to know when to apply the synchronized keyword to methods.
To lessen the load on the programmer, the Java API provides a library of
atomic primitives in the java.util.concurrent.atomic package. These are
classes with certain operations guaranteed to execute atomically. For example,
the AtomicInteger class encapsulates the functionality of an int variable
with atomic accesses. One of its methods is incrementAndGet(), which will
atomically increment its internal value by 1 and return the result. Recall from
Program 14.1 that even an operation as simple as
++ isn’t atomic. If many different threads try to increment a single
variable, some of those increments can get lost, causing the final value
to be less than it should be.
We can use the AtomicInteger class to rewrite
Program 14.1 so that no race condition occurs.
AtomicInteger.import java.util.concurrent.atomic.*;
public class NoRaceCondition extends Thread {
private static AtomicInteger counter = new AtomicInteger();
public static final int THREADS = 4;
public static final int COUNT = 1000000;
public static void main(String[] args) {
NoRaceCondition[] threads = new NoRaceCondition[THREADS];
for(int i = 0; i < THREADS; i++) {
threads[i] = new NoRaceCondition();
threads[i].start();
}
try {
for(int i = 0; i < THREADS; i++)
threads[i].join();
}
catch(InterruptedException e) {
e.printStackTrace();
}
System.out.println("Counter:\t" + counter.get());
}
public void run() {
for(int i = 0; i < COUNT / THREADS; i++)
counter.incrementAndGet();
}
}This program is identical to Program 14.1, except
that the type of counter has been changed from int to
AtomicInteger (and an appropriate import has been added).
Consequently, the ++ operation was changed to an incrementAndGet()
method call, and a get() method call was needed to get the final
value. If you run this program, the final answer should always be
1,000,000, no matter what.
The java.util.concurrent.atomic package includes AtomicBoolean and
AtomicLong as well as AtomicInteger. Likewise, the
AtomicIntegerArray and AtomicLongArray classes are included to
perform atomic array accesses. For general purposes, the
AtomicReference<V> class provides an atomic way to store a reference
to any object. The <V> is a generic type parameter, which will be
discussed in Chapter 18.
Although you could use the synchronized keyword to create each one of
these classes yourself, the result wouldn’t be as efficient. The atomic
classes use a special lock-free mechanism. Unlike the synchronized
keyword which forces a thread to acquire a lock on a specific object,
lock-free mechanisms are built on a compare-and-swap (CAS) hardware
instruction. Thus, incrementing and the handful of other ways to update an
atomic variable execute in one step because of special instructions on the
CPU. Since there’s no waiting to acquire a lock or fighting over which thread
has the lock, the operation is very fast. Many high performance concurrent
applications depends on CAS implementations.
17.6. Exercises
Conceptual Problems
-
Explain the difference between static binding and dynamic binding. In which situations does each apply?
-
Consider the following two classes.
public class Sale { public double discount = 0.25; public double getDiscount() { return discount; } public void setDiscount(double value) { discount = value; } }public class Blowout extends Sale { public double discount = 0.5; public double getDiscount() { return discount; } public void setDiscount(double value) { discount = value; } }Given the following snippet of code, what’s the output and why?
Sale sale = new Blowout(); System.out.println(sale.discount); System.out.println(sale.getDiscount); Blowout blowout = (Blowout)sale; System.out.println(blowout.discount); sale.setDiscount(0.75); System.out.println(sale.discount); -
What are the differences and similarities between abstract classes and interfaces?
-
Assume that the
Corn,Carrot, andPotatoclasses are all derived fromVegetable. BothCarrotandPotatoclasses have apeel()method, butCorndoes not. Examine the following code and identify which line will cause an error and why.Vegetable[] vegetables = new Vegetable[30]; for(int i = 0; i < vegetables.length; i += 3) { vegetables[i] = new Corn(); vegetables[i + 1] = new Carrot(); vegetables[i + 2] = new Potato(); } int index = vegetables.length - 1; Potato potato; while(index >= 0) { potato = (Potato)vegetable[index]; potato.peel(); index--; } -
How many different structures can the keyword
finalbe applied to in Java, and what doesfinalmean in each case? -
Assume that
Quicksandis a child class ofDanger.What’s the output of the following code and why?
Quicksand quicksand = new Quicksand(); if(quicksand instanceof Danger) { System.out.printf("Run for your lives!"); if(quicksand.getClass() == Danger.class) System.out.printf("Run even faster!"); if(quicksand instanceof Quicksand) { System.out.printf("The more you struggle, the faster you'll sink!"); if(quicksand.getClass() == Quicksand.class) System.out.printf("You'll need to find a vine to escape!"); -
Consider the following two classes. What’s the problem that prevents compilation?
public class Snake { public void handle() throws BiteException { System.out.println("You handled a snake!"); if(Math.random() > 0.9) throw new BiteException(); } }public class Cobra extends Snake { public void handle() throws BiteException, PoisonException { System.out.println("You handled a cobra!"); if(Math.random() > 0.8) { if(Math.random() > 0.2) throw new PoisonException(); throw new BiteException(); } } }
Programming Practice
-
Update the solution from Section 11.5 so that it uses as many of the inheritance tools from this chapter as possible. Clearly, the
Gate,UnaryOperator, andBinaryOperatorclasses should be markedabstract. Which methods should beabstract? Which methods or classes should befinal? -
Implement a program to assess income tax on normal employees, students, and international students using a class hierarchy. Normal employees pay a 6.2% social security tax and a 1.45% Medicare tax every year, but neither kind of student pays these taxes. All three groups pay normal income tax according to the following table.
Marginal Tax Rate Income Bracket 10%
$0 - $9,700
12%
$9,701 - $39,475
22%
$39,476 - $84,200
24%
$84,201 - $160,725
32%
$160,726 - $204,100
35%
$204,101 - $510,300
37%
$510,301+
Tax is assessed at a given rate for every dollar in the range. For example, if someone makes $35,000, she pays 10% tax on the first $9,700 of her income and 12% on the remaining $25,300. The exception is international students whose country has a treaty with the U.S. so that they don’t have to pay tax on the first $50,000 of income.
-
Re-implement the original
SynchronizedAccountclass from Example 14.2 using atomic classes. For simplicity, you can change thebalancetype fromdoubletoAtomicIntegersince there’s noAtomicDoubleclass. How much has this simplified the implementation? Is thereadersfield still necessary? Why or why not?
Experiments
-
Take Program 17.4 and increase
COUNTto100000000. Run it several times and time how long it takes to run to completion.Then, take Program 14.1 and increase its
COUNTto100000000as well. Change the body of theforloop inside therun()method so thatcount++;is inside of asynchronizedblock that usesRaceCondition.classas the lock. (The choice ofRaceCondition.classis arbitrary, but it’s an object that all the threads can see.) In this way, the increment will occur atomically, since only the thread that has acquired theRaceCondition.classlock will be able to do the operation. Now, run this modified program several times and time it.How different are the running times? They might be similar, depending on the implementation of locks and CAS on your OS and hardware platform.
18. Dynamic Data Structures
Algorithms + Data Structures = Programs
18.1. Problem: Infix conversion
If a math teacher writes the expression 1 + 7 × 8 - 6 × (4 + 5) ÷ 3 on the blackboard and asks a group of 10-year-old children to solve it, different children might give different answers. The difficulty lies not in the operations themselves but in the order of operations. Modern graphing calculators and many computer programs can, of course, evaluate such expressions correctly, but how do they do it? You intuitively grasp order of operations (left to right, multiplication and division take higher precedence than addition and subtraction, and so on), but encoding that intuition into a computer program requires effort.
One way a computer scientist might approach this problem is to turn the mathematical expression from one that’s difficult to evaluate into one that’s easy. The normal style of writing mathematical expressions is called infix notation, because the operators are written in between the operands they’re used on. An easier notation for automatic evaluation is called postfix notation, because an operator is placed after the operands it works on. The following table gives a few examples of expressions written in both infix and postfix notation.
| Infix | Postfix |
|---|---|
|
|
|
|
|
|
|
|
Although infix notation is probably more familiar to you, postfix notation has the benefit of exactly specifying the order of operations without using any precedence rules and without needing parentheses to clarify. To understand how to compute an expression in postfix notation, we rely on the idea of a stack, which we first introduced in Chapter 9 and examine in greater depth here.
Recall that a stack has three operations: push, pop, and top. It works like a stack of physical objects. The push operation places an object on the top, the pop operation removes an item from the top, and the top operation tells you what’s at the top of the stack.
Using a stack, postfix evaluation rules are easy: Scan the expression from left to right, if you see an operand (a number, in our case), put it on the stack. If you see an operator, pop the last two operands off the stack and use the operator on them. Then, push the result back on the stack. When you run out of input, the value at the top of the stack is your answer.
For example, with 1 9 2 * +, all three operands are pushed onto the
stack. Then, the * is read, and so 2 and 9 are popped off the stack
and multiplied. The result 18 is pushed back on the stack. Then, the
+ is read, and 18 and 1 are popped off the stack and summed,
resulting in 19, which is pushed back on the stack as the final
answer.
Our problem, however, is not to evaluate an expression in postfix notation but to convert an expression in infix notation to postfix notation. Again, the concept of a stack is useful. To do the conversion, we initialize a stack and scan through the input in infix notation. As we scan through the input, we do one of four things depending on which of the four possible inputs we see.
- Operand
-
Simply copy the operand to the postfix output.
- Operator
-
If the stack’s empty, push the operator onto the stack. If the stack’s not empty and the operator at the top of the stack has the same or greater precedence than our new operator, put the top operator into our postfix output and pop the stack. Continue this process as long as the top operator has the same or greater precedence compared to our new operator and the stack is not empty. Finally, push the new operator onto the stack.
- Left Parenthesis
-
Push the left parenthesis onto the stack.
- Right Parenthesis
-
Pop everything off the stack and add it to the output until you reach a left parenthesis on the stack. Then pop the left parenthesis.
Precedence comes from order of operations: * and / have high
precedence and ` and `-` have low precedence. When you encounter it on
the stack, treat `(` as if it has even lower precedence than ` and
-. A right parenthesis should never appear on the stack.
Following this algorithm, we’re able to write a program that converts infix notation to postfix notation. We further restrict our problem to the case when the only operands are positive integers in the range [0, 9]. Since each is a single character, parsing the input is much easier. The same ideas for postfix conversion hold no matter how the input is formatted, but parsing arbitrarily formatted numbers is a difficult problem in its own right. This restriction also makes spaces unnecessary.
To solve the infix conversion problem, we need to create a stack data structure whose elements are terms from an infix expression, where a term is an operator, operand, or a parenthesis. We created a stack to solve the nesting expression problem in Section 9.1, but we explore stacks in this chapter as one of many different kinds of dynamic data structure.
18.2. Concepts: Dynamic data structures
By now you’ve seen several ways to organize data in your programs. For example, you’ve used arrays to store a sequence of values and class definitions to store (and operate on) collections of related values in objects. These data structures have the property that they’re static in size: Once allocated, they do not grow as the program runs. If you allocate an array to store 100 integers, you’ll get an error if you try to store 101 integers into it.
In this chapter, we examine dynamic data structures: As more data is read or processed, these data structures grow and shrink in memory to store what is needed. The stack used to solve the nesting expressions problem from Chapter 9 was not actually a dynamic data structure since it was defined with a fixed maximum size. In this chapter, we implement a true stack as well as many other kinds of dynamic data structures.
18.2.1. Dynamic arrays
There are two broad classes of dynamic data structures we examine here. The first kind are based on arrays that grow and shrink. Dynamic arrays allow for fast access to individual elements in the data structure. One drawback of dynamic arrays is that the array that stores that data has a fixed amount of space. When too many elements are added, a new array must to be allocated and all the original elements copied over.

14 would need to be moved back to insert 17 in order.Another drawback of dynamic arrays is that they’re poorly suited for insertion or deletion of elements in the middle of the array. When an element is inserted, each element after it must be moved back one position. Likewise, when an element is deleted, all of the elements after it must be moved forward one position. Thus, insertions and deletions at the end of a dynamic array are usually efficient, but insertions and deletions in the middle are time consuming.
18.2.2. Linked lists
The second kind of dynamic data structure is based on objects that link
to (or reference) other objects. The simplest form of such a data type
is a linked list. A linked list is a data structure made up of a
sequence of objects. Each object contains some data value (such as a
String) and a link to the next object in the sequence.

Linked lists are flexible because they have no preset size. Whenever a new element is needed, it can be created and linked into the list. Unfortunately, they can be slow if you need to access arbitrary elements in the list. The only way to reach an element in the list is to walk from element to element until you find what you’re looking for. If the element is at the beginning (or the end) of the list, this process can be quick. If the element is in the middle, there’s no fast way to get there.
Linked lists work well when inserting new elements at arbitrary locations in the list. Unlike arrays, they’re not implemented as a contiguous block of memory. Linking a new element into the middle of the list automatically creates the correct relationship among elements, and there’s no need to move all the elements after an insertion.
Among their downsides is the memory overhead of linked lists. A new object must be allocated for each element in the list, which must include a reference to the next element as well as its own data. Consequently, using a linked list to solve a problem usually take more memory than an equivalent dynamic array solution.
It turns out that either dynamic arrays or linked lists can be used to create an efficient solution to the infix conversion problem defined at the beginning of the chapter.
18.2.3. Abstract data types
The fact that dynamic arrays and linked lists can be used to solve similar problems points out that we may often be more interested in the capabilities of a data structure rather than its implementation.
An abstract data type (ADT) is a set of operations that can be applied to a set of data values with well-defined results that are independent of any particular implementation. In other words, it is a list of things that a data type can do (or have done to it).
A stack is a great example of an ADT. A stack needs to be able to push a value, pop a value, and tell us what value is on top. The internal workings of the stack are irrelevant (as long as they’re efficient). It’s possible to use either a dynamic array or a linked list to implement a stack ADT. A queue is another ADT we discuss in Section 18.4, but there are many other useful ADTs.
18.3. Syntax: Dynamic arrays and linked lists
18.3.1. Dynamic arrays
Suppose you’re faced with the problem of reading a list of names from a
file, sorting them into alphabetical order, and printing them out. You’ve
already looked at simple sorting algorithms to handle the sorting
part, or you could use the Java Arrays.sort() method. In previous
problems when you needed to use an array for storing items, you knew in
advance how many (or a maximum of how many) items you’d need to store.
In this new problem, the number of names in the input file is
unspecified, so you must allow an arbitrary number to be handled.
One approach is to make a guess at how many names are in the input file and allocate an array of that size. If your guess is too small, and you don’t check array accesses, you’ll cause an exception once you’ve filled the array and try to store the next name into the index one past the last legal one. If your guess is too large, you could be wasting a significant amount of storage space.
Our first solution to the problem of dealing with dynamic or unknown amounts of data is to watch our array accesses and expand the array as necessary during processing. It’s also possible to contract an array once you determine that the array has more space than needed.
A simple solution
Program 18.1 allocates an array of 10 String references
and reads a list of names from standard input until it reaches the end
of the file, storing each name in successive array locations. If the
number of names in the input is larger than the size of the array, it
generates an exception.
Since programs that generate uncaught exceptions are, in general, a bad idea, our first change to this program should be either to catch the exception or check the index before storing the name in the array. In either case, we would then take some action that’s more user friendly than generating an exception, perhaps simply printing an explanatory message before exiting.
import java.util.Arrays;
import java.util.Scanner;
public class ReadIntoFixedArray {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String[] names = new String[10];
int count = 0;
while(in.hasNextLine())
names[count++] = in.nextLine();
Arrays.sort(names, 0, count);
for(String name: names) (1)
System.out.println(name);
}
}| 1 | Note that we use an enhanced for loop for convenient iteration through
the array names. If you don’t recall this syntax, refer to
Section 6.9.1. |
A second possibility is to take a recovery action that allows the program to proceed. What went wrong? We made a guess of the input size and allocated an array of that size, but our guess was too small. We could modify the code to allocate a larger array at the beginning, recompile, and re-run the program, but that option might not be available to us if the program’s been distributed to users around the world. Instead, we fix the problem on the fly by allocating a larger array, copying the old array into the new array, and continuing.
Program 18.2 begins like the previous program by allocating a fixed-size array.
import java.util.Arrays;
import java.util.Scanner;
public class ReadAndGrowArray {
public static void main(String[] args) {
String[] names = new String[10];
Scanner in = new Scanner(System.in);
int count = 0;
String line = null;
while(in.hasNextLine()) {
line = in.nextLine();
try {
names[count] = line;
}
catch(ArrayIndexOutOfBoundsException e) { (1)
names = Arrays.copyOfRange(names, 0, names.length*2); (2)
names[count] = line;
}
count++;
}
Arrays.sort(names, 0, count);
for(String name: names)
System.out.println(name);
}
}| 1 | The program catches the ArrayOutOfBoundsException if there isn’t enough
space for another name in the array. |
| 2 | The catch statement allocates a new array, twice the size of the original
(current) array, copies the existing array into it, and replaces the reference
to the current array with a reference to the new array. |
Note that it was necessary to refactor the code in
Program 18.1 slightly. We added the line variable
to hold the temporary result of reading the input line and moved the
count increment outside of the try-catch block.
Can this new, improved program still fail? Yes, but only for very large input, in the case when the Java virtual machine runs out of memory when doubling the size of the array.
A potentially more serious problem is the way we set names to point at
a new array.
names = Arrays.copyOfRange(names, 0, names.length*2);This line works because we know the only variable that references the
array is names. If other variables referenced that array, they would
continue to reference the old, smaller, and now out-of-date version of
the names array. Figure 18.3 shows this problem.

array1 and array2 begin pointing at the same array. (b) A new array has been allocated, and 42 has been added to it. array1 has been updated to point at the new array, but array2 still points at the original.A more complete solution
The problem of updating variables that reference the dynamic array is a serious issue in large programs. It might not be enough to allocate a larger array and assign the new reference to only one variable. There might be hundreds of variables (or other objects) that reference the original array.
A solution to this problem is to create a new class whose objects
contain the array as a private field. References to the array are then
mediated, as usual, via accessor methods, which always refers to the
same version of the array. Program 18.3 is a simple
implementation of a dynamic array class. This class maintains an
internal array of String objects, which it extends whenever a call to
set() tries to write a new element just past the end of the array.
import java.util.Arrays;
public class DynamicArray {
private String[] strings = new String[10];
public synchronized void set(int i, String string) {
if(i == strings.length)
strings = Arrays.copyOfRange(strings, 0, strings.length*2);
strings[i] = string;
}
public String get(int i) {
return strings[i];
}
public synchronized void sort(int first, int last) {
Arrays.sort(strings, first, last);
}
}Note that the set() and sort() methods are both synchronized in
case this class is used by multiple threads simultaneously.
Program 18.4 illustrates how to modify and extend Program 18.1 to use this new class. Since the array grows automatically, there is no need for the original program to check for out-of-bounds exceptions. Of course, the array expansion only works if the reference occurs exactly at the index corresponding to one beyond the end of the array. Other out-of-bound references generate an exception.
DynamicArray class to store input read from a file.import java.util.Scanner;
public class UseDynamicArray {
public static void main(String[] args) {
DynamicArray names = new DynamicArray();
Scanner in = new Scanner(System.in);
int count = 0;
String line = null;
while(in.hasNextLine()) {
line = in.nextLine();
names.set(count, line); (1)
count++;
}
names.sort(0, count); (2)
for(int i = 0; i < count; i++) (3)
System.out.println(names.get(i));
}
}| 1 | Since names is no longer an array, but rather an object of class
DynamicArray, we can no longer use braces ([]) to access elements and
must use methods set() and get() instead. |
| 2 | Arrays.sort() can’t sort this object directly which is why we provided a
sort() method in the class that sorts the private array on demand. |
| 3 | We also can’t use an enhanced for loop on names and must iterate through
its contents explicitly. |
This implementation, like most implementations of dynamic arrays, has potentially serious performance penalties. If the initial array is too small, it will have been doubled and the elements copied multiple times, resulting in slower execution. After a resize, the array is only half full, resulting in wasted space. Even on average, the array will only be three-quarters full.
18.3.2. Linked lists
As we’ve seen, while dynamic arrays can grow to accommodate a large number of items, the performance penalties of repeated copying and the space wasted by unoccupied array elements can negatively affect program behavior. In this section, we introduce the linked list, an alternative data structure that can efficiently grow to accommodate a large number of objects. As we shall see, this efficient growth comes at the expense of limitations on how the structure can be accessed.
Consider again the problem of reading an arbitrary number of names from an input file and storing them. Since we don’t know in advance how many names there are, it might not be efficient to pre-allocate or dynamically grow an array to store them. Instead, imagine that we could write each name on a small index card, and then link the index cards together to keep track of them, much like the cars of a railroad train are linked by the coupling from one to the next.
Constructing a linked list
In Java, a linked list is usually implemented as a class that provides methods to interact with a sequence of objects. The objects in the list are implemented as a private static nested class. A private static nested class behaves like a normal class but can only be created and accessed by the class surrounding it. In this way, the internal representation of the list is hidden and protected from outside modification. The nested class has two fields, one containing the data to be stored and the other containing a link or reference to the next object, or node, in the list. Since they’re only accessed by the outer class, it’s reasonable to make these fields public. If you need a refresher on static nested classes, refer to Section 9.4.
public class LinkedList {
private static class Node {
public String value;
public Node next;
}
// Methods for interacting with the list
}Note that the type next is the same as the class it’s inside of! This
apparent circular reference works because the variable only references
an object, but the object is not actually contained within the variable.
In fact, the value of the link may be null, indicating that there are
no additional nodes in the list.
In the railroad metaphor, the node is a train car (with its freight as the value), and the link to the next node is the coupling to the next car.
The definition of LinkedList given above is a good start, but it needs
a head reference that keeps track of the first node in the list.
Initially, this value is null. We also need an add() method so that
we can add nodes to the list. Without checking through the entire list,
it’s useful to know how many nodes are in it. We can create a size
field that we increment whenever we add a node, as well as an accessor
to read its value. Finally, we can create a fillArray() method that
fills an array with the values in the list.
String objects.public class LinkedList {
private static class Node {
public String value;
public Node next;
}
private Node head = null;
private int size = 0;
public void add(String value) {
Node temp = new Node();
temp.value = value;
temp.next = head;
head = temp;
size++;
}
public int size() {
return size;
}
public void fillArray(String[] array) {
Node temp = head;
int position = 0;
while(temp != null) {
array[position++] = temp.value;
temp = temp.next;
}
}
}Program 18.6 is a re-implementation of the
name-reading program using class LinkedList. Note that no array needs
to be pre-allocated. Instead, we capture all lines of input in a
linked list called list.
LinkedList class to store input read from a file.import java.util.Arrays;
import java.util.Scanner;
public class UseLinkedList {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
LinkedList list = new LinkedList();
while(in.hasNextLine())
list.add(in.nextLine());
String[] names = new String[list.size()];
list.fillArray(names);
Arrays.sort(names);
for(String name: names)
System.out.println(names);
}
}Each time we read a new line from the file, the LinkedList class
internally creates a new Node with the input line as its value. It
also sets its next reference to the current head so that the rest
of the list (which could be empty if head is null) comes after the
new Node. We then update the head field to reference the new Node.
Thus, each new line read from the file is stored at the beginning of
the linked list. The last node in the list, which contains the first
String read in, has a next value of null.
Figure 18.4 shows a visualization of the contents of this
implementation of a linked list. An “X” is used in place of an arrow
that points to null.

Since we also increment the size field inside of LinkedList on each
add, we know how many String objects it contains. Thus, we know how large of
an array to allocate in Program 18.6. The fillArray() method visits
every node in the linked list, storing its value into the allocated array.
array. We sort the returned array and then print it as before.
Appending to the end of a linked list
The LinkedList class maintains a field named head that references
the first node in the linked list. As we saw, that element was actually
the last or most recent String read from input. This head
element was followed by the next most recent String, followed by the
next most recent String, and so on. The last node contained the first
String read from input and had a null next field.
If we want the linked list to be ordered in the natural way, with head
pointing to the first element read from the file and the last element in
the list (the one with next pointing to null) containing the
String most recently read, we can maintain a second field that
references the tail of the list.
Program 18.7 adds a tail pointer called
tail to the LinkedList class. Note that we have changed the add()
method to the addFirst() method, and we have also added an addLast()
method to make it easy to append elements to the end of a linked list.
tail, to reference the last element (tail) of the list.public class LinkedListWithTail {
private static class Node {
public String value;
public Node next;
}
private Node head = null;
private Node tail = null;
private int size = 0;
public void addFirst(String value) { (1)
Node temp = new Node();
temp.value = value;
temp.next = head;
head = temp;
if(tail == null)
tail = head;
size++;
}
public void addLast(String value) { (2)
Node temp = new Node();
temp.value = value;
if(tail == null)
head = temp;
else
tail.next = temp;
tail = temp;
size++;
}
public int size() {
return size;
}
public void fillArray(String[] array) {
Node temp = head;
int position = 0;
while(temp != null) {
array[position++] = temp.value;
temp = temp.next;
}
}
}| 1 | The addFirst() method has been updated to change the tail
pointer, but only if the list is empty (when head is null). After all,
adding to the front of a list only changes tail if the front is also
the back. |
| 2 | In the addLast() method, adding a value to an empty list
also sets the head to point at the new node. Once the list has a node in it,
subsequent calls to addLast() will point the next field of
the old tail at this new node, linking the earlier nodes in the list to the
new node at the end. |
Inserting into a linked list
In the running example for this chapter, we’re interested in printing a
sorted list of String objects read from input. Thus far we’ve
captured the lines into a linked list of elements, dumped these elements
into an array of the right size, and then sorted the array. An
alternative solution is to insert the elements into the linked list at
the right point in the first place.
Program 18.8 is a version of a linked list that
inserts elements into the linked list in sorted order. The only
significant difference between it and the previous implementations of a
linked list is its add() method. This method walks down the linked
list, starting at head, until it either walks off the end of the list
or finds an element before which the new String should go. There are
special cases that must be handled to make this process work correctly:
empty list, inserting at the beginning, inserting in the middle, and inserting
at the end.
add() method inserts each value in sorted order.public class SortedLinkedList {
private static class Node {
public String value;
public Node next;
}
private Node head = null;
private Node tail = null;
private int size = 0;
public void add(String value) {
Node temp = new Node();
temp.value = value;
temp.next = null;
if(head == null) // Empty list (1)
head = tail = temp;
else if(value.compareTo(head.value) < 0) { // Insert at beginning (2)
temp.next = head;
head = temp;
}
else { // Insert at middle or end (3)
Node previous = head;
Node current = head.next;
while(current != null && value.compareTo(current.value) >= 0) {
previous = current;
current = current.next;
}
previous.next = temp;
temp.next = current;
if(current == null) // Inserting at end of list (4)
tail = temp;
}
size++;
}| 1 | When adding to an empty linked list, the head and tail fields must be set to
reference the new node. The next field of the new node is null by default. |
| 2 | If inserting at the beginning of a non-empty list, the head must be
updated to point to the new node. The next field of the new node is set to
the old value of head. |
| 3 | Inserting into the middle or the end of a linked list are similar
operations. To insert a node into the middle, it’s common to maintain two
variables to reference the current and previous nodes while walking down
the list. Once the proper insertion point is found (between the previous and
current nodes), the next field for the previous node is adjusted to
reference the new node, and next field for the new node is set to current. |
| 4 | Inserting at the end of a linked list is the same as inserting into the
middle, except that the tail field must also be updated to reference the new
node. |
public int size() {
return size;
}
public void fillArray(String[] array) {
Node temp = head;
int position = 0;
while(temp != null) {
array[position++] = temp.value;
temp = temp.next;
}
}
}18.4. Syntax: Abstract data types (ADT)
We’ve seen two examples so far of dynamic data structures: dynamic arrays and linked lists. A great deal of complexity can go on inside these data structures, but code that uses these data structures doesn’t need to be aware of the details of the internal implementation. Ideally, user programs could use any data structure that provides the required set of operations.
Our dynamic array and linked list classes were simple examples of abstract data types (ADT). We can design many data structures that hide the details of their implementation inside a class. The user of each class is aware of the operations (public methods) that can be performed on objects of the class but not of the intricacies used to implement those operations. Defining an ADT without regard to an implementation keeps users of the ADT from becoming dependent on details of any particular implementation. It gives maximum freedom to the programmer to choose (and change) the implementation as appropriate for the overall system design.
We generalize a data structure by observing which operations are applied to it. Then, we create an abstraction that formalizes these observations. The idea is to cleanly separate the use and behavior of the data structure from the way in which it’s implemented.
Interfaces are the obvious tool for defining the behavior of a class in Java without specifying its implementation. When defining an ADT in Java, its set of operations becomes the set of methods specified by the interface. Then, any class that implements the ADT must implement the corresponding interface.
In subsequent sections we look at two fundamental abstract data types, stacks and queues, and sample classes that implement them.
18.4.1. Stacks
We’ve already used stacks to solve problems in Chapter 9. Recall that a stack data structure behaves like a stack of books on your desk. When you place a book on the stack, it covers the books that are already there. When you take a book off the stack, you remove the book most recently placed there, exposing the one beneath it.
You can find a simple implementation of a stack in the solution to the infix conversion problem in Section 18.6, but we now examine the stack more deeply as an archetypal ADT. A stack’s restricted set of operations (pushing and popping) is adequate for many tasks and can be implemented in a number of different ways, some more efficient than others.
The acronym FILO (first in, last out) is sometimes used to describe a stack. The last item that’s been pushed onto the stack is the first item to be popped off the stack. In the next section, we’ll study the queue, which is a FIFO (first in, first out) data structure.
18.4.2. Abstract Data Type: Operations on a stack
There are two essential operations on a stack abstract data type,
corresponding to placing a book on the pile and removing it: push()
and pop(). We also define two additional operations, top() and
isEmpty().
-
push(x)
Push valuexonto the stack. -
pop()
Pop the object off the top of the stack and return its value. -
top()
Return the value from the top of the stack but do not remove it. -
isEmpty()
Returntrueif the stack is empty andfalseotherwise.
Because a stack’s an abstract data type, we’re not specifically
concerned with how these operations are implemented, merely that they
are. Thus, we can specify an interface called Stack that requires
these four methods.
public interface Stack {
void push(String value);
String pop();
String top();
boolean isEmpty();
}Linked list implementation
All the operations defined by the stack ADT (and interface) are
implemented as methods in the class LinkedListStack, shown in
Program 18.10.
public class LinkedListStack implements Stack {
private static class Node {
public String value;
public Node next;
}
private Node head = null; (1)
public void push(String value) { (2)
Node temp = new Node();
temp.value = value;
temp.next = head;
head = temp;
}
public String pop() { (3)
String value = null;
if(isEmpty())
System.out.println("Can't pop empty stack!");
else {
value = head.value;
head = head.next;
}
return value;
}
public String top() {
String value = null;
if(isEmpty())
System.out.println("No top on an empty stack!");
else
value = head.value;
return value;
}
public boolean isEmpty() {
return head == null;
}
}| 1 | The head field is used to maintain a reference to the linked list that
defines the stack. It is initialized to null. |
| 2 | The method push() must create a new node for the linked list and push
it onto the front of the list. It does so by creating a new Node,
setting its value field to the incoming value, and pointing its
next pointer to the beginning of the list, stored by head. Since
temp is now the new top of the stack, head is made to point at it. |
| 3 | The pop() method needs to return the value of the head node and
remove that node from the linked list. It does this by replacing the
head node with the node pointed at by the next link in head. The
pop() method from the simpler stack used in the solution to the nested
expressions problem in Section 9.5 merely
removed the top and didn’t return the value. Most real-world stack
implementations of pop() do return this value, giving programmers
more flexibility. |
Note that both pop() and top() print an error message if the stack
is empty. More elaborate error handling is possible by throwing an exception.
Dynamic array implementation
Like the dynamic array example of Program 18.3,
Program 18.11 implements a stack of String
values using a dynamic array data structure.
import java.util.Arrays;
public class DynamicArrayStack implements Stack {
private String[] strings = new String[10];
private int size = 0;
public void push(String string) {
if(size == strings.length)
doubleArray();
strings[size++] = string;
}
public String pop() {
String value = null;
if(size == 0)
System.out.println("Can't pop empty stack!");
else
value = strings[--size];
return value;
}
public String top() {
String value = null;
if(isEmpty())
System.out.println("No top on an empty stack!");
else
value = strings[size - 1];
return value;
}
public boolean isEmpty() {
return size == 0;
}
private void doubleArray() {
strings = Arrays.copyOfRange(strings, 0, strings.length*2);
}
}This stack implementation using a dynamic array omits the top() and
isEmpty() methods, causing a compiler error until the Stack interface is
fully implemented.
At the beginning of the chapter, we introduced the problem of converting an expression from infix to postfix notation. In Section 18.6, we give the solution to this problem, but without a program that can evaluate a postfix expression, the conversion tool isn’t very useful.
Here we give a simple postfix evaluator. Recall the algorithm: Scan the input expression from left to right, if you see a number, put it on the stack. If you see an operator, pop the last two operands off the stack and use the operator on them. Then, push the result back on the stack. When you run out of input, the value at the top of the stack is your answer.
Like the infix to postfix converter, we restrict our input to positive
integers of a single digit. To make this program simpler, we introduce
two new classes that will be useful in our infix to postfix converter.
The first is Term.
public class Term {
private int value;
public Term(int value) { this.value = value; }
public int getValue() { return value; }
}This class allows us to hold an int value. Although its structure is
simple, we update the definition of Term later in the solution to the
infix to postfix conversion problem. By doing so, we can keep exactly
the same definition for TermStack given next.
Term objects.public class TermStack {
private static class Node {
public Term value;
public Node next;
}
private Node head = null;
public void push(Term value) {
Node temp = new Node();
temp.value = value;
temp.next = head;
head = temp;
}
public Term pop() {
Term value = null;
if (isEmpty())
System.out.println("Can't pop empty stack!");
else {
value = head.value;
head = head.next;
}
return value;
}
public Term top() {
Term value = null;
if (isEmpty())
System.out.println("No top on an empty stack!");
else
value = head.value;
return value;
}
public boolean isEmpty() {
return head == null;
}
}This class gives a linked list implementation of a stack. In fact, it’s
virtually identical to Program 18.10 with the
substitution of Term for String.
With our utility classes in place, the code for the postfix evaluator is short.
import java.util.*;
public class PostfixEvaluator {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String expression = in.nextLine(); (1)
TermStack stack = new TermStack();
for(int i = 0; i < expression.length(); i++) { (2)
char term = expression.charAt(i);
if(term >= '0'&& term <= '9') (3)
stack.push(new Term(term - '0'));
else {
int b = stack.pop().getValue();
int a = stack.pop().getValue();
switch(term) { (4)
case '+': stack.push(new Term(a + b));
break;
case '-': stack.push(new Term(a - b));
break;
case '*': stack.push(new Term(a * b));
break;
case '/': stack.push(new Term(a / b));
break;
}
}
}
System.out.println("The answer is: " + stack.top().getValue()); (5)
}
}| 1 | Our main() method reads in the expression from the user and
creates a TermStack called stack. |
| 2 | Then, it iterates through the
expression with a for loop. |
| 3 | For each number we find, we supply it as
an argument to the constructor of a new Term object, which we push
onto stack. |
| 4 | For each operator, we pop two items off stack and apply the operator
to them. We create a new Term from the result and push this value onto
stack. |
| 5 | Finally, after all input is exhausted, we print the value on
the top of stack. |
To test this program properly, you must supply expressions in postfix form. Also, remember that these operations are all integer operations without fractional parts. Be careful to avoid division by zero!
18.4.3. Queues
A queue data structure is similar to a stack data structure, except that when getting an item from a queue, the item that’s been in the queue longest is the one retrieved. A queue data structure models an ordinary queue or line of people. The first person in line at a bank, for example, is the first one to receive service. Late comers are served in the order in which they arrive.
A queue is sometimes called a FIFO (first in, first out) data structure due to this property. To distinguish the operations on a queue from those on a stack, we use the terms enqueue and dequeue instead of push and pop.
18.4.4. Abstract Data Type: Operations on a queue
Four typical operations on a queue data structure are the following.
-
enqueue(x)
Put valuexat the end of the queue. -
dequeue()
Remove and return the value at the front of the queue, that is, the value that’s waiting the longest. -
front()
Return the value at the front of the queue but do not remove it. -
isEmpty()
Returntrueif the queue is empty andfalseotherwise.
As with stacks, we can specify an interface called Queue that requires
these four methods.
public interface Queue {
void enqueue(String value);
String dequeue();
String front();
boolean isEmpty();
}Linked list implementation
Program 18.15 shows an implementation of the queue
ADT operations using a linked list. Because we need to keep track of
nodes at both ends of the linked list, we maintain head and tail
variables to reference these nodes. The enqueue() and dequeue()
methods manipulate these variables to manage the queue as values are put
onto it and removed from it.
public class LinkedListQueue implements Queue {
private static class Node {
public String value;
public Node next;
}
private Node head = null;
private Node tail = null;
public void enqueue(String value) {
Node temp = new Node();
temp.value = value;
temp.next = null;
if(isEmpty())
head = temp;
else
tail.next = temp;
tail = temp;
}
public String dequeue() {
String value = null;
if(isEmpty())
System.out.println("Can't dequeue an empty queue!");
else {
value = head.value;
head = head.next;
if(head == null)
tail = null;
}
return value;
}
public String front() {
String value = null;
if(isEmpty())
System.out.println("No front on an empty queue!");
else
value = head.value;
return value;
}
public boolean isEmpty() {
return head == null;
}
}Note that the implementation of the LinkedListQueue class is very
similar to the implementation of the LinkedListWithTail class. The
enqueue() method in the former is almost identical to the addLast()
method in the latter.
18.5. Advanced: Generic data structures
Most of the dynamic data structures we’ve seen in this chapter store
values of type String. We’ve explored dynamic arrays of String values,
linked lists of String objects, queues of String objects, and stacks
of String objects. In Example 18.1, we
created the stack class TermStack to hold Term objects, but
TermStack is identical to the existing LinkedListStack class with
the substitution of Term for String.
What if you wanted to store values of some other type in these data
structures? What if you wanted a stack of int values or a queue of
Thread objects? You might think that you need to create a distinct but
similar implementation of each ADT for each type, as we do in
Example 18.1.
One possible solution is to take advantage of the fact that a variable
of type Object can hold a reference to a value of any reference type,
since all classes are subtypes of Object. If we create data
structures using Object as the underlying type, we can store values of
any type in the data structure. For example,
Program 18.16 is an implementation of a stack ADT with
an underlying data type of Object.
Object references.public class ObjectStack {
private static class Node {
public Object value;
public Node next;
}
private Node head = null;
public void push(Object value) {
Node temp = new Node();
temp.value = value;
temp.next = head;
head = temp;
}
public Object pop() {
Object value = null;
if(isEmpty())
System.out.println("Can't pop empty stack!");
else {
value = head.value;
head = head.next;
}
return value;
}
public Object top() {
Object value = null;
if(isEmpty())
System.out.println("Can't get top of empty stack!");
else
value = head.value;
return value;
}
public boolean isEmpty() {
return head == null;
}
}A stack of Object references could be an example of a
heterogeneous data structure since it’s possible to push objects of
different types onto the same stack. While there are situations in which
this technique is useful, in most cases a homogeneous data structure
(where all values are of the same type) is all that’s needed.
Homogeneous data structures allow type checking to occur at compile
time, thus helping to avoid run-time errors.
Using a stack of Object references is generally more cumbersome, since
you must cast values returned from pop() or top() to the appropriate
data type.
ObjectStack stack = new ObjectStack();
stack.push("hello");
String result = (String)stack.pop(); (1)| 1 | Without the explicit cast to String, the compiler gives an error:
Type mismatch: cannot convert from Object to String. |
Casting the returning value from a heterogeneous data structure essentially forces type checking to move from compile time to run time. Instead of having the Java compiler verify the type correctness of operations, we force the Java virtual machine to do the check.
18.5.1. Generics in Java
Java provides a general facility to create classes that implement the
same basic ADT but with a different underlying data type. This mechanism
preserves the advantages of compile-time type checking and eliminates
the need for run-time casting. A generic class is a class that gives a
template for creating classes in which a placeholder for an underlying
data type can be filled in when a specific instance of that class is
created. In the case of Example 18.1, we need
a stack that can hold Term objects instead of String objects, and a
generic class would allow us to create a stack of any reference type.
The generics facility in Java only supports underlying data types that
are reference types like String and other classes, not
primitive types like int or boolean. However, we can use
wrapper classes to hold primitives types. Thus, a generic stack of int
values needs to be implemented as a stack of Integer objects.
Fortunately, Java automatically converts between int and Integer in
most cases.
Defining a simple generic class in Java is done by appending a type
parameter within angle brackets (<>) to the end of the class name
being defined.
public class GenericClass<T> {
...
T transform(T item) {
...
}
}This code defines a new generic class (think class template)
GenericClass with underlying type T. It includes a method
transform() that takes a value of type T and transforms it (in some
unspecified way) to another value of type T.
To use a generic class properly, you must create instances of it
specifying the underlying type. Then, the compiler will check using the
appropriate type at compile time. The compiler must make sure that
all the operations are valid with the supplied type substituted for the
type parameter (T in this example).
For example, to create and use an instance of GenericClass with
underlying type String, you might do the following.
GenericClass<String> genericString = new GenericClass<String>();
String output = generic.transform("hello");Because this use of the GenericClass class is defined for underlying
type String, no casting is necessary to assign the result of the
transform() method to the String variable output.
To create and use an instance of GenericClass with underlying type
Integer, you would type:
GenericClass<Integer> genericInteger = new GenericClass<Integer>();
int i = generic.transform(27);The same definition of GenericClass is used in both instances with
different underlying data types, and the compiler is able to verify at
compile time that the uses are type safe.
If you omit the underlying type when declaring a generic variable or
creating an instance of a generic type, the compiler uses Object as
the underlying type. This use, called a raw type, is essentially like
not using generics at all. There’s no compile-time type checking, and
references must be cast as needed. Modern Java compilers generally issue
a warning when raw types are used.
GenericClass genericRaw = new GenericClass(); // Raw type
int i = (Integer)genericRaw.transform(27); // Cast neededThe next two examples illustrate defining generic classes in Java.
Program 18.17 defines a generic version of the
LinkedList class shown earlier. Note that it’s necessary to include
the type parameter T on the outer class as well as the nested class
Node.
public class GenericLinkedList<T> {
private static class Node<T> {
public T value;
public Node<T> next;
}
private Node<T> head = null;
private int size = 0;
public void add(T value) {
Node<T> temp = new Node<T>();
temp.value = value;
temp.next = head;
head = temp;
size++;
}
public int size() {
return size;
}
public void fillArray(T[] array) {
Node<T> temp = head;
int position = 0;
while(temp != null) {
array[position++] = temp.value;
temp = temp.next;
}
}
}This class is almost indistinguishable from Program 18.5 except that
is uses type T instead of String.
Using generics is mostly like using any other class, but there are a few
oddities. In particular, there are problems instantiating arrays with generic
types. The fillArray() method works because it never creates the array, only
fills it.
18.5.2. Using a Generic Class
Creating an instance of a generic class is similar to creating an
instance of a regular class, except that you should
specify the missing type (or types) used to parameterize the generic
class. For example, if you want to create an instance of the
GenericClass<T> class, you must specify the type T, for example
new GenericClass<String>().
Program 18.18 uses the generic class
GenericLinkedList parameterized by String to re-implement
Program 18.6.
GenericLinkedList to create and use a linked list of Strings.import java.util.Arrays;
import java.util.Scanner;
public class UseGenericLinkedList {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
GenericLinkedList<String> list = new GenericLinkedList<String>();
while(in.hasNextLine())
list.add(in.nextLine());
String[] names = new String[list.size()];
list.fillArray(names);
Arrays.sort(names);
for(String name: names)
System.out.println(name);
}
}Java 7 and later allow generic type inference. Type inference means that
the compiler is able to guess what type you mean without explicitly typing it.
Type inference is intended as a convenience so that you don’t have to type as
much repetitive code. The most common form of generic type inference uses the
diamond operator (<>). This operator is used when instantiating a generic
type to show the compiler that you want to use a generic type parameter that
you believe the compiler can determine for itself.
For example, the following line appears above without type inference.
GenericLinkedList<String> list = new GenericLinkedList<String>();Using type inference, it can be shortened to the following.
GenericLinkedList<String> list = new GenericLinkedList<>();In general, you must always type the full generic type parameter when declaring a variable, but you can often use the diamond operator when instantiating a new generic object.
18.5.3. Using Java Libraries
Many Java library classes use generics to make them more flexible. The
java.util package includes many classes to implement stacks, queues,
dynamic arrays, sets, and other useful data structures. These container classes
are parameterized so that they can be created to hold many different types. We
illustrate three examples here: Vector, ArrayList, and HashMap. Note that
there’s also a LinkedList class, which is a great deal more powerful than the
LinkedList class defined in this chapter. Any class that implements the
Iterable interface can also be used in the enhanced for loops described in
Section 6.9.1. The ArrayDeque, ArrayList, HashSet, TreeSet,
and Vector classes all implement Iterable. In our examples, a Vector
object and a Set (returned by the entrySet() method of a HashMap) are
used as targets of enhanced for loops.
A Vector (java.util.Vector) implements an array of objects that can
grow at run time. The array is automatically extended whenever an
attempt is made to store an item exactly one location beyond the last
element. Unlike a linked list, Vector elements can be efficiently
accessed in any order (by specifying the index, just like an ordinary
array). An element can be inserted into the middle of the Vector,
causing any elements after the insertion point to be pushed back by an index.
Arbitrary elements can also be deleted from the Vector using the remove()
method.
Program 18.19 illustrates a use of the Vector
class. The program creates an empty Vector and generates random
integers between 1 and 10, appending them to the end of the vector,
until their sum is at least 100. Then, it prints the integers, their
sum, and how many were generated.
import java.util.Random;
import java.util.Vector;
public class VectorExample {
public static void main(String[] args) {
Random random = new Random();
Vector<Integer> vector = new Vector<Integer>();
int sum = 0;
while(sum < 100) {
int n = random.nextInt(10) + 1;
vector.add(n); // append n to end of vector
sum += n;
}
for(int n: vector)
System.out.format("%3d%n", n);
System.out.println("---");
System.out.format("%3d (%d values)%n", sum, vector.size());
}
}Output from a typical run of Program 18.19 is shown below:
9 9 8 7 7 4 7 6 8 7 9 4 9 10 --- 104 (14 values)
The HashMap(java.util.HashMap) is a very useful, general-purpose
data structure that maintains a dictionary of entries. A dictionary
associates unique keys with values. You can think of it as mapping a
key to a value. In the Java HashMap class, keys and values can be
arbitrary Java classes.
Program 18.20 reads a sequence of lines containing
names and ages. For simplicity, each name is one word, and each age is a
simple integer. It stores these (name, age) pairs in a
HashMap<String,Integer> data structure. Once all the input is read and
in.hasNext() returns false, the program prints all the keys
(names), then all the values (ages), and finally it prints the names and
ages of each person in the input file.
HashMap dictionary to store a mapping from names to ages.import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
public class HashMapExample {
public static void main(String[] args) {
HashMap<String,Integer> map = new HashMap<>();
Scanner in = new Scanner(System.in);
while(in.hasNext()) {
String name = in.next();
int age = in.nextInt();
map.put(name, age);
}
System.out.println("Keys");
for(String name: map.keySet())
System.out.println("\t" + name);
System.out.println("Values");
for(int age: map.values())
System.out.println("\t" + age);
for(Map.Entry<String, Integer> entry: map.entrySet())
System.out.println(entry.getKey() + " -> " + entry.getValue());
}
}Shown below is the output for a simple input file.
Keys Kathy Martha Fred Henway Michael Henry John Margarette Edward Tim Hamcost Values 60 22 15 1 21 31 23 57 12 57 2 Kathy -> 60 Martha -> 22 Fred -> 15 Henway -> 1 Michael -> 21 Henry -> 31 John -> 23 Margarette -> 57 Edward -> 12 Tim -> 57 Hamcost -> 2
18.6. Solution: Infix conversion
Here we give our solution to the infix conversion problem from the
beginning of the chapter. As in Example 18.1,
we use a stack of Term objects to solve the problem. However, we
expand the Term class to hold both operands and operators. We only add
methods and fields to the earlier definition, taking nothing away. In
this way, we should be able to use the Term class for both infix to
postfix conversion and postfix calculation.
public class Term {
private int value;
private char operator;
private boolean isOperator;Here we’ve augmented the earlier Term class by adding two more
fields, a char called operator to hold an operator and a boolean
called isOperator to keep track of whether or not our Term object
holds an operator or an operand.
public Term(int value) {
this.value = value;
isOperator = false;
}
public Term(char operator) {
this.operator = operator;
isOperator = true;
}We now have two constructors. The first one takes an int value and
stores it into value, setting isOperator to false to indicate that
the Term object must be an operand. The second constructor takes a
char value and stores it into operator, setting isOperator to
true to indicate that the Term object must be an operator (such as
+, -,*, or /).
public int getValue() { return value; }
public char getOperator() { return operator; }
public boolean isOperator() { return isOperator; } These three accessors give back the operand value, the operator
character, and whether or not the object is an operator, respectively.
This solution is not necessarily the most elegant from an OOP
perspective. The code that uses a Term object needs to choose the
getOperator() method or the getValue() method depending on whether
the Term is an operator. This design opens up the possibility
that some code will call the wrong accessor method and get a useless
default value.
public boolean greaterOrEqual(Term term) {
if(isOperator())
switch(operator) {
case '*':
case '/': return true;
case '+':
case '-': return term.operator != '*' && term.operator != '/';
default: return false;
}
else
return false;
}
}The most complicated addition to the Term class is the
greaterOrEqual() method, which takes in another Term object. This
method compares the operator of the Term object being called with the
one that’s being passed in as a parameter. Because this method is in
the Term class, it can access the private variables of the term
parameter. This method returns true if the operator of the called
object has a greater or equal precedence compared to the operator of the
parameter object. The meat of the method is the switch statement that
establishes the high precedence of * and /, the medium precedence of
+ and -, and the low precedence of anything else, namely the left
parenthesis (.
With this updated Term class, we can create Term objects that hold
either an operator or an operand and allow the precedence of operators
to be compared. We use exactly the same TermStack class from
Example 18.1 for our stack. All that remains
is the client code that parses the input.
import java.util.*;
public class InfixToPostfix {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String expression = in.nextLine(); (1)
TermStack stack = new TermStack(); (2)
String postfix = ""; (3)| 1 | We read in the input expression. |
| 2 | We create a TermStack called stack to aid in conversion. |
| 3 | We also declare an empty String called postfix to hold the output. |
for(int i = 0; i < expression.length(); i++) { (1)
char term = expression.charAt(i);
if(term >= '0' && term <= '9') (2)
postfix += term;
else if(term == '(') (3)
stack.push(new Term(term));
else if(term == ')') { (4)
while(stack.top().getOperator() != '(') {
postfix += stack.top().getOperator();
stack.pop();
}
stack.pop(); // Pop off the '('
}
else if(term == '*' || term == '/' || term == '+' || term == '-') {
Term operator = new Term(term); (5)
while(!stack.isEmpty() && stack.top().greaterOrEqual(operator)) {
postfix += stack.top().getOperator();
stack.pop();
}
stack.push(operator);
}
}| 1 | This for loop runs through each char in the input expression and
applies the four rules given in the description of the infix conversion
problem. |
| 2 | If a term is an operand, it’s added directly to the output. |
| 3 | If a term is a left parenthesis, it’s pushed onto the stack. |
| 4 | If a term is a right parenthesis, all the terms on the stack are popped off and added to the output until a left parenthesis is reached. |
| 5 | If a term is a normal operator, the top of the stack is repeatedly popped
and added to output as long as it has a precedence greater than or equal to the
new operator. The complexity of doing this precedence comparison is tucked
away inside of the Term class. |
while(!stack.isEmpty()) { (1)
postfix += stack.top().getOperator();
stack.pop();
}
System.out.println(postfix); (2)
}
}| 1 | After the input has all been consumed, we pop any remaining operators off the stack and add them to the output. |
| 2 | Finally, we print the output. |
The output from this program could be used as the input to the postfix
evaluator program from Example 18.1. A more complex program
that did both the conversion and the calculation might want to store
everything in a queue of Term objects instead of producing String output and
then recreating Term objects.
18.7. Concurrency: Linked lists and thread safety
The implementations of stacks and queues in the previous sections are
not thread-safe. If multiple threads use a stack or queue object
simultaneously, the head or tail pointers can become inconsistent or
be updated incorrectly, potentially causing the stack or queue to lose
elements. As you’ve seen, multiple threads operating on the same data
can produce unexpected results.
Program 18.21 is a simple multi-threaded program to test (and break!) the thread safety of the queue implementation in Program 18.15.
public class UseLinkedListQueue extends Thread {
private static final int THREADS = 10;
private LinkedListQueue queue;
private boolean adding;
public static void main(String[] args) throws InterruptedException {
Thread[] threads = new Thread[THREADS];
LinkedListQueue queue = new LinkedListQueue(); (1)
for(int i = 0; i < THREADS; i++) {
threads[i] = new UseLinkedListQueue(queue, true);
threads[i].start(); (2)
}
for(int i = 0; i < THREADS; i++)
threads[i].join(); (3)
for(int i = 0; i < THREADS; i++) {
threads[i] = new UseLinkedListQueue(queue, false);
threads[i].start(); (4)
}
for(int i = 0; i < THREADS; i++)
threads[i].join();
while(!queue.isEmpty())
System.out.println("Left in queue: ID = " + queue.dequeue());
}| 1 | The program creates a queue. |
| 2 | It then creates and starts 10 threads, passing them the queue and true
for their adding value. |
| 3 | Then, the program joins the threads until each has finished. |
| 4 | The program starts 10 more threads, passing them the same queue but false
for their adding value. |
public UseLinkedListQueue(LinkedListQueue queue, boolean adding) { (1)
this.queue = queue;
this.adding = adding;
}
public void run() {
if(adding) {
long ID = Thread.currentThread().getId();
System.out.println("Thread ID added to queue: " + ID);
queue.enqueue("" + ID); (2)
}
else {
String ID = queue.dequeue();
System.out.println("Thread ID removed from queue: " + ID); (3)
}
}
}| 1 | Each thread’s constructor takes a reference to the shared queue and a
boolean that specifies whether it’s an adding or a removing thread. |
| 2 | Threads in the adding phase add a String version of their thread ID
numbers to the queue and print it out. |
| 3 | Threads not in the adding phase each remove one value from the queue and print it out. |
Without appropriate synchronization, the program may not correctly link all values into the queue nor remove them at the end. A typical error-prone output run is shown here.
Thread ID added to queue: 9 Thread ID added to queue: 14 Thread ID added to queue: 13 Thread ID added to queue: 12 Thread ID added to queue: 11 Thread ID added to queue: 10 Thread ID added to queue: 18 Thread ID added to queue: 17 Thread ID added to queue: 16 Thread ID added to queue: 15 Thread ID removed from queue: 14 Thread ID removed from queue: 11 Thread ID removed from queue: 12 Thread ID removed from queue: 16 Thread ID removed from queue: 17 Thread ID removed from queue: 18 Thread ID removed from queue: 10 Can't dequeue an empty queue! Can't dequeue an empty queue! Thread ID removed from queue: 15 Thread ID removed from queue: null Thread ID removed from queue: null
How does this implementation fail? Consider the situation in which two
threads are attempting to put a value in the queue simultaneously by calling
the enqueue() method in Program 18.15. Suppose
the first thread tests the queue and finds it empty (isEmpty() returns
true) but is then interrupted. If a second thread gets control, it will
also see that the queue’s empty, set the head and tail
variables to the new Node object temp, and
return. The first thread will eventually wake up, still thinking that
the queue is empty, and also set the head and tail variables to its
own new Node temp. But these assignments overwrite the assignments
just done by the previous thread! The initial node that was in the queue
is now lost. Note that there are other sequences of execution that can cause
similar race conditions.
This problem can be fixed by ensuring that once one thread starts
examining and modifying queue variables, no other thread can access the
same variables until the first one is finished. As shown in
Chapter 14, this mutual exclusion can be
achieved by using the synchronized keyword on methods that need to
have exclusive access to object variables. In this queue implementation,
we need to synchronize access by threads that are using either the
enqueue() or dequeue() methods, since both methods access and
manipulate variables in the object. Although it’s not called in this
program, the front() method should also be synchronized so that a
null head is not accessed accidentally. The isEmpty() method doesn’t
need to be synchronized since the only methods that call it that can
do any harm are already synchronized. Outside code that calls
isEmpty() might get the wrong value if another thread modifies the
contents of the queue, but there’s no guarantee that other threads won’t
modify the state of the queue at any point after the isEmpty()
method is called anyway.
public class LinkedListQueueSafe implements Queue {
private static class Node {
public String value;
public Node next;
}
private Node head = null;
private Node tail = null;
public synchronized void enqueue(String value) {
Node temp = new Node();
temp.value = value;
temp.next = null;
if(isEmpty())
head = temp;
else
tail.next = temp;
tail = temp;
}
public synchronized String dequeue() {
String value = null;
if(isEmpty())
System.out.println("Can't dequeue an empty queue!");
else {
value = head.value;
head = head.next;
if(head == null)
tail = null;
}
return value;
}
public synchronized String front() {
String value = null;
if(isEmpty())
System.out.println("No front on an empty queue!");
else
value = head.value;
return value;
}
public boolean isEmpty() {
return head == null;
}
}With both enqueue() and dequeue() methods synchronized as in
Program 18.22, a typical output generated by the
program is shown below.
Thread ID added to queue: 9 Thread ID added to queue: 14 Thread ID added to queue: 12 Thread ID added to queue: 13 Thread ID added to queue: 10 Thread ID added to queue: 11 Thread ID added to queue: 18 Thread ID added to queue: 17 Thread ID added to queue: 16 Thread ID added to queue: 15 Thread ID removed from queue: 9 Thread ID removed from queue: 18 Thread ID removed from queue: 13 Thread ID removed from queue: 17 Thread ID removed from queue: 15 Thread ID removed from queue: 16 Thread ID removed from queue: 14 Thread ID removed from queue: 12 Thread ID removed from queue: 10 Thread ID removed from queue: 11
18.8. Concurrency: Thread-safe libraries
As we mentioned in Section 9.6, some libraries are thread safe and some are not. The Java Collections Framework (JCF) is a very useful library, but it’s also a library that requires you to manage your own thread safety if it matters for your program.
The JCF defines the Collection interface and the Map interface. The
Collection interface, which any collection of objects should
implement, has subinterfaces Set, List, and Queue which define the
basic operations in Java that are needed to implement a set, list, or
queue of items. The Map interface gives the basic operations for a
dictionary, a collection of key-value pairs, one implementation of which
is the HashMap from Example 18.4.
As we mentioned in Chapter 10, an interface can’t
mark a method with the synchronized keyword. Consequently, the JCF makes
no guarantee about the thread safety of a container based on which
interface it implements. The programmer must read the documentation
carefully in order to know if a container is thread safe and react accordingly.
An ArrayList is like a Vector, with essentially the same interface
but without synchronization. That is, if two threads attempt to insert or
remove an element from the same ArrayList at the same time, the
internal state of the ArrayList might become corrupt, or the results might be
incorrect.
Program 18.23 is an example of synchronizing updates to the
ArrayList class with multiple threads.
ArrayList.import java.util.ArrayList;
public class ArrayListExample extends Thread {
private ArrayList<String> list;
public static void main(String[] args) throws InterruptedException {
ArrayList<String> list = new ArrayList<String>(); (1)
Thread t1 = new ArrayListExample(list); (2)
Thread t2 = new ArrayListExample(list);
t1.start();
t2.start();
t1.join();
t2.join();
for(String text: list) (3)
System.out.println(text);
}| 1 | The main() method creates an ArrayList. |
| 2 | It then creates and starts two threads, passing in the ArrayList as an
argument to each so that they both share the list. |
| 3 | After waiting for the threads to finish, the main() method prints
out the contents of the list. |
public ArrayListExample(ArrayList<String> list) {
this.list = list; (1)
}
public void run() {
for(int i = 0; i < 10; i++) { (2)
synchronized(list) { (3)
list.add(this.getName() + ": " + i);
}
try {
Thread.sleep(1); (4)
}
catch (InterruptedException e) {
e.printStackTrace();
}
}
}
}| 1 | The constructor stores a reference to the shared ArrayList. |
| 2 | Each thread repeats a loop 10 times, appending a String to the
ArrayList on each iteration. |
| 3 | To prevent concurrent updates from happening, each thread
synchronizes on the shared variable list. |
| 4 | To make concurrent update attempts more likely without synchronization, the thread sleeps for a millisecond on each iteration. |
Without the synchronized keyword, a typical run, shown below,
includes a null reference in the output, indicating that the internal
ArrayList data structure wasn’t updated correctly.
Thread-1: 0 Thread-0: 0 Thread-1: 1 Thread-0: 1 Thread-1: 2 Thread-0: 2 Thread-0: 3 Thread-1: 3 Thread-1: 4 Thread-0: 4 null Thread-0: 5 Thread-1: 6 Thread-0: 6 Thread-1: 7 Thread-0: 7 Thread-1: 8 Thread-0: 8 Thread-0: 9 Thread-1: 9
With the synchronized keyword, each run includes exactly the same
number of entries from each thread, although the threads don’t always
alternate in strict lockstep.
Thread-0: 0 Thread-1: 0 Thread-0: 1 Thread-1: 1 Thread-1: 2 Thread-0: 2 Thread-1: 3 Thread-0: 3 Thread-1: 4 Thread-0: 4 Thread-0: 5 Thread-1: 5 Thread-1: 6 Thread-0: 6 Thread-1: 7 Thread-0: 7 Thread-1: 8 Thread-0: 8 Thread-1: 9 Thread-0: 9
ArrayList is much more widely used than Vector, not in spite of its lack
synchronization but because of that lack. Synchronization tools have overhead,
slowing down execution. Most programmers aren’t focused on writing thread-safe
code and prefer faster execution.
Whenever synchronization doesn’t matter, ArrayList is clearly a better choice
than Vector. When synchronization does matter, the programmer must decide
whether to use Vector or to use ArrayList with explicit synchronization
tools.
18.9. Exercises
Conceptual Problems
-
Explain the difference between static data structures and dynamic data structures.
-
In which situations is it better to use a dynamic array? In which situations is it better to use a linked list? Explain why in each case.
-
On which line in Program 18.1 is an exception generated? Why?
-
In Program 18.2, is it possible to post-increment
countinside thetryclause rather than at the bottom of thewhileloop? -
Explain why the array inside the
namesobject in Program 18.4 is, on average, only three-quarters full. -
Based on the stack implementation in Program 18.10, draw a picture of the linked list structure after each of the following statements.
LinkedListStack stack = new LinkedListStack(); stack.push("hello"); stack.push("goodbye"); stack.pop(); stack.push("there"); stack.push("cruel"); stack.pop(); stack.push("world"); -
Implement the methods
top()andisEmpty()for the dynamic array implementation of the stack in Program 18.11. -
Based on queue implementation in Program 18.15, draw a picture of the linked list structure after each of the following statements.
LinkedListStack queue = new LinkedListStack(); stack.enqueue("hello"); stack.enqueue("there"); stack.enqueue("world"); stack.dequeue(); stack.enqueue("cruel"); stack.dequeue(); stack.enqueue("goodbye");
Programming Practice
-
Implement a version of
DynamicArrayfrom Program 18.3 that shrinks the size of its internal storage array to half its size when only one quarter of its capacity is being used. This design can save significant amounts of space if a large number of items are added to the dynamic array at once and then removed. -
Consider Program 18.7 which defines the
LinkedListWithTailclass for storing a linked list ofStringvalues. Add areverse()method to the class which reverses the order of the nodes in the linked list. The key idea is make a new linked list that holds the head of the list. Then, remove the head from the original linked list. Put the next node in front of the head in the new linked list and remove it from the old. Continue the process until there’s nothing left in the original list. Be sure to reset theheadandtailreferences correctly after the reversal. -
In Section 18.2.2, we used two kinds of linked lists to store data but copy all that data back into an array before sorting it. We also used a third linked list class,
SortedLinkedList, to insert data and maintain a sorted order. However, it’s possible to add data in non-sorted order to a linked list and then sort it afterward. Add asort()method to theLinkedListWithTailclass that performs a bubble sort on the nodes inside.The algorithm for a bubble sort is described in Section 10.1. The idea is to make repeated passes through a list, swapping two adjacent items if they’re out of order. You keep making passes over the list until no adjacent items are out of order. For a this
sort()method, you’ll need to use thecompareTo()method to compare theStringvalues in the linked list nodes. Also, it might be necessary to have special cases that update theheadandtailpointers if those nodes are swapped with other nodes. Note that bubble sort is not the fastest way to sort a linked list. We introduce a faster approach in Chapter 19. -
Create JUnit test cases to verify that the
synchronizedkeywords are needed on theset()andsort()methods of theDynamicArrayexample from Program 18.3. To test theset()method, you can create one thread that repeatedly sets, gets, and tests a changing value at a fixed location (e.g., 0) and another thread that continuously appends to the array (causing it to grow by copy and replace, thus occasionally overwriting the value at the fixed location). To test thesort()method, create two threads that sort the same large random array at the same time. Check to see if the array is, in fact, actually sorted after the threads have exited. For both tests, you might need to repeat the operations a number of times to trigger the race condition. -
To make an infix converter that can handle floating-point values or even just integers with more than one digit, you need to make a pass over the input, parsing the sequence of characters into terms. When an expression is in infix notation, the order of terms is an operand followed by an operator, repeated over and over, and finishing on an operand. There are two exceptions: Whenever you’re expecting an operand, you might get a left parenthesis, but after the parenthesis, you’ll continue to look for an operand. Whenever you’re expecting an operator, you might get a right parenthesis, but after that parenthesis, you’ll continue to look for an operator.
Using this first pass over input to separate terms as well as the
Double.parseDouble()method to compute the equivalentdoublevalues of operands, rewrite the solution from Section 18.6 to convert your terms into postfix ordering and then calculate the answer. -
Re-implement the solution to the infix conversion problem given in Section 18.6 so that it uses
GenericStackwith a type parameter ofTerminstead ofTermStack. -
Interfaces can also be generic. Consider the following generic version of
Queue.public interface Queue<T> { void enqueue(T value); T dequeue(); T front(); boolean isEmpty(); }Re-implement
LinkedListQueueso that it’s generic with type parameterTand implements interfaceQueue<T>.
Experiments
19. Recursion
In order to understand recursion, you must first understand recursion.
19.1. Problem: Maze of doom
The evil mastermind from Chapter 13 has returned with a new attempt at world domination. Since he now knows that you can use concurrency to crack his security code, this time he’s hidden his deadly virus in a secret location protected by a complex maze of walls and passageways. Fortunately, you’ve been able to get a copy of the maze floor plan, but now you must write a program to find a path through it so you can steal the deadly virus before the evil mastermind unleashes it on the world.

Finding a path through a maze involves systematically exploring twists
and turns, keeping track of where you’ve been, backtracking out of dead
ends, and producing a resulting path once you make it through. You
already have the basic tools necessary to solve this problem. You can,
for example, represent the maze with a two-dimensional array of
characters, where a plus (''+) represents a wall and a space (' ')
represents a passageway. You could mark a path through the maze by
replacing a contiguous (vertical and horizontal but not diagonal)
sequence of ' ' characters by '*' characters, leading from the
starting square to the final square where the deadly virus is located.
The difficulties are dead ends and, worse, loops. How do you keep track of which paths you’ve tried that didn’t work? While you could use additional data structures to store this information, recursion is a solution technique that makes solving problems like this one surprisingly straightforward.
19.2. Concepts: Recursive problem solving
The idea that we’ll use to solve this maze problem is called recursion. Imagine you’re in a maze and have the choice to go right, left, or straight. No matter which of the three paths you take, you’ll probably be confronted by more choices of going right, left, or straight as you progress. You need to explore them all systematically. The process of systematically exploring the right path is similar to the process of systematically exploring the left path. The choice at this moment between left, right, and straight is in fact part of the same systematic process you want to follow when you’re in the left, right, or straight branches of the maze.
Solutions that can be described in terms of themselves are recursive. But what is recursion? How can describing something in terms of itself be useful? Since recursion sounds circular, how can it be applied to problem solving in Java? How does the computer keep track of these self-references? The following subsections address these questions.
19.2.1. What is recursion?
In the context of computer science and mathematics, recursion means describing some repetitive process in terms of itself. Many complex things can be described elegantly using recursion.
Consider the question, “How old are you now?” If you’re 27, you could answer, “I’m one year older than I was last year.” If then asked, “Well, how old were you last year?” Again, you could answer, “I was one year older than I was the year before.” Assuming that the person who wanted to wanted to know your age was very patient, you could repeat this answer over and over, explaining that each year you’ve been one year older than the previous year. However, after being asked 27 times about your age on the previous year, you’d run out of years of life and be forced to answer, “Zero years old.”
This absurd dialog shows an important feature of useful recursive definitions: They have at least one base case and at least one recursive case. The base case is the part of the definition that’s not described in terms of itself. It’s a concrete answer. Without the base case, the process would never end, and the definition would be meaningless. The recursive case is the part of the definition that is defined in terms of itself. Without the recursive case, the definition could only describe a finite set of things.
In the example above, the base case is being zero years old. You have no age before that. The recursive case is any age greater than zero . We can use mathematical notation to describe your age in a given year. Here age(year) is a function that gives the age you were during year.

To be meaningful, recursive cases should be defined in terms of simpler or smaller values. In English, it’s equally correct to say that you are now a year younger than you’ll be next year. Unfortunately, the age that you’ll be next year is not any closer to a base case, making that recursion useless.

A recursive definition for your age suggests that recursion is all around us. Though recursive definitions written in formal notation might seem artificial, self-similarity is a constant theme in art and nature. The branching of a trunk of a tree is similar to the branching of its limbs, which is similar to the branching of its branches, which in turn is similar to the branching of its twigs. In fact, we borrow the idea of the branching of a tree to define a recursive data structure in Section 19.4. Figure 19.2 starts with a simple Y-shaped branching. By successively replacing the branches with the previous shape, a tree is generated recursively. Fractals are images generated by similar recursive techniques. Although many real trees exhibit recursive tendencies, they don’t follow rules consistently or rigidly.
19.2.2. Recursive definitions
Although recursion crops up throughout the world, certain forms of recursion are more useful for solving problems. As with many aspects of programming, the recursion we use has a strong connection to mathematical principles.
In mathematics, a recursive definition is one that is defined in terms of itself. It’s common to define functions, sequences, and sets recursively. Functions, such as f(n), are usually defined in relation to the same function with a smaller input, such as f(n - 1). Sequences, such as sn, are usually defined in relation to earlier elements in the sequence, such as sn-1.
Even very common functions can be defined recursively. Consider the multiplication x · y. This multiplication means repeatedly adding x a total of y times. If y is a positive integer, we can describe this multiplication with the following recursive definition. Note the base case and recursive case.

Multiplication seems like such a basic operation that there would be no need to have such a definition. Yet mathematicians often use multiple equivalent definitions to prove results. Furthermore, this elementary definition provides intuition for creating more complex definitions.
Another mathematical function with a natural recursive definition is the factorial function, often written n!. The factorial function is used heavily in probability and counting. The value of n! = n · (n - 1) · (n - 2) · … · 3 · 2 · 1. Mathematicians like recursive definitions because they’re able to describe functions and sequences precisely without using ellipses (…).

Note that the base case gives 1 as the answer when n = 0. By convention 0! = 1. Thus, this definition correctly gives 0! = 1, 1! = 1 · 0! = 1, 2! = 2 · 1! = 2, 3! = 3 · 2! = 6, and so on.
The Fibonacci sequence is an infinite sequence of integers starting with 1, 1, 2, 3, 5, 8, 13, 21, …. Each term after the two initial 1s is the sum of the previous two terms in the sequence. Fibonacci has many interesting properties and crops up in surprisingly diverse areas of mathematics. It was originally developed to model the growth of rabbit populations.
The Fibonacci sequence also has a natural recursive mathematical definition. Indeed, you may have noticed that we described each term as the sum of the two previous terms. We can formally define the nth Fibonacci number Fn as follows, starting with n = 0.

Since the Fn depends on the two previous terms, it’s necessary to have two base cases. The Fibonacci sequence is a special kind of Lucas sequence. Other Lucas sequences specify different values for the two base cases and sometimes coefficients to multiply the previous terms by.
19.2.3. Iteration vs. recursion
These mathematical definitions are interesting, but what’s their
relationship to Java code? So far, we’ve considered algorithms that
are iterative in nature: processing is performed as a sequence of
operations on elements of a sequential data structure. We sum the
elements of an array by iterating through them from first to last. We
multiply two matrices by using nested for loops to sequence through
the matrix contents in the proper order. Similarly, one method might make
a sequence of one or more calls to other methods. We’re confident that
such computations terminate because we start at the beginning and work
to the end of a finite structure. But what if the structure is not a
simple linear or multidimensional array? The path we’re trying to find
through the maze is of unknown length and complexity.
A method might call other methods to complete its operation. For example,
a method that sorts a list of String values calls another method to do
pairwise comparison of the values in the list. A method that calls
itself, either directly or indirectly, is called a recursive method.
A recursive method might seem like a circular argument that never ends. In fact, a recursive method only calls itself under certain circumstances. In other circumstances, it does not. A recursive method has the same two parts that a mathematical recursive definition has.
-
Base case
The operation being computed is done without any recursive calls. -
Recursive case
The operation is broken down into smaller pieces, one or more of which results in a recursive call to the method itself.
Each time a method calls itself recursively it does so on a smaller problem. Eventually, it reaches a base case, and the recursion terminates.
A recursive method is useful when a problem can be broken down into smaller subproblems where each subproblem has the same structure as the original, complete problem. These subproblems can be solved by recursive calls and the results of those calls assembled to create a larger solution.
Recursive methods are often surprisingly small given their complexity. Each recursive call only makes a single step forward in the process of solving the problem. In fact, it can appear that the problem is never solved. The code has something like a “leap of faith” inside of it. Assuming you can solve a smaller subproblem, how do you put the solutions together to solve the full problem? This assumption is the leap of faith, but it works out as long as the subproblems get broken down into smaller and smaller pieces that eventually reach a base case.
From a theoretical standpoint, any problem that can be solved iteratively can be solved recursively, and vice versa. Iteration and recursion are equivalent in computational power. Sometimes it’s more efficient or more elegant to use one approach or the other, and some languages are designed to work better with a particular approach.
19.2.4. Call stack
Many programmers who are new to recursion feel uncomfortable about the syntax. How can a method call itself? What does that even mean?
Recursion in Java is grounded in the idea of a call stack. We discuss the stack abstract data type in Chapter 18. A similar structure is used to control the flow of control of a program as it calls methods.
Recall that a stack is a first in, last out (FILO) data structure. Each time a method is called, its local variables are put on the call stack. As the method executes, a pointer to the current operation it’s executing is kept on the call stack as well. This collection of local variables and execution details for a method call is called the stack frame or activation record. When another method is called, it pushes its own stack frame onto the call stack as well, and its caller remembers what it was executing before the call. When a method returns, it pops its stack frame (the variables and state associated with its execution) off the call stack.
A recursive method is called in exactly the same way. It puts another copy of its stack frame on the call stack. Each call of the method has its own stack frame and operates independently. There’s no way to access the variables from one call to the next, other than by passing in parameters or returning values.
Figure 19.3 shows the stack frames being pushed
onto the call stack as the main() method calls the factorial()
method, starting with the argument 4. The factorial() method
recursively calls itself with successively smaller values.

Figure 19.4 shows the stack frames popping off
the call stack as each call to factorial() returns. As the answers are
returned, they’re incorporated into the answer that’s generated and
returned to the next caller in the sequence until the final answer 24
(4!) is returned to main().

19.3. Syntax: Recursive methods
Unlike many Syntax sections in other chapters, there’s no new Java syntax to introduce here. Any method that calls itself, directly or indirectly, is a recursive method. Recursive methods are simply methods like any others, called in the normal way.
The real difficulty in learning to program recursively lies in breaking out of the way you’re used to thinking about program control flow. All that you’ve learned about solving problems with iteration in previous chapters might make it harder for you to embrace recursion.
Iteration views the whole problem at once and tries to sequence all the pieces of the solution in some organized way. Recursion is only concerned with the current step in the solution. If the current step is one in which the answer is clear, you’re in a base case. Otherwise, the solution takes one step toward the answer and then makes the leap of faith, allowing the recursion to take care of the rest. Programmers who are new to recursion are often tempted to do too much in each recursive call. Don’t rush it!
The use of recursion in languages like Java owes much to the development of functional programming. In many functional languages (such as Scheme), there are no loops, and only recursion is allowed. In a number of these languages, there’s no assignment either. Each variable has one value for its entire lifetime, and that value comes as a parameter from whatever method called the current method.
It may seem odd to you, but this approach is a good one to follow when writing recursive methods. Try not to assign variables inside your methods. See if the work done in each method can be passed on as an argument to the next method rather than changing the state inside the current method. In that way, each recursive method is a frozen snapshot of some part of the process of solving the problem. Of course, this guideline is only a suggestion. Many practical recursive methods need to assign variables internally, but a surprisingly large number do not.
Because the data inside these methods is tied so closely to the input
parameters and the return values given back to the caller, these methods
are often made static. Ideally, recursive methods do not change the
state of fields or class variables. Again, sometimes changing external
state is necessary, but recursive methods are meant to take in only
their input parameters and give back only return values. Recursive code
that reads and writes variables inside of objects or classes can be
difficult to understand and debug since it depends on outside data.
With this information as background, we focus on examples for the rest of this section. Because recursion is a new way of thinking, approach these examples with an open mind. Many students have the experience that recursion makes no sense until they see the right example. Then, the way it works suddenly “clicks.” Don’t be discouraged if recursion seems difficult at first.
In this section, we work through examples of factorial computation, Fibonacci numbers, the classic Tower of Hanoi problem, and exponentiation. These problems are mathematical in nature because mathematical recursion is easy to model in code. The next section applies recursion to processing data structures.
In our first example of a recursive implementation, we return to the factorial function. Recall the recursive definition that describes the function.

By translating this mathematical definition almost directly into Java, we can generate a method that computes the factorial function.
public static long factorial(int n) {
if(n == 0) // Base case
return 1;
else // Recursive case
return n * factorial(n-1);
}Note the base case and recursive case are exactly the same as in the
recursive definition. The return type of the method is long because
factorial grows so quickly that only the first few values are small
enough to fit inside of an int.
Let’s return to the recursive definition of Fibonacci.

Like factorial, this definition translates naturally into a recursive method in Java.
public static int fibonacci(int n) {
if(n == 0 || n == 1) // Base cases
return 1;
else // Recursive case
return fibonacci(n-1) + fibonacci(n-2);
}One significant problem with this implementation is performance. In this case, the double recursion performs a great deal of redundant computation.
One technique for eliminating redundant computation in recursion is called memoization. Whenever the value for a subproblem is computed, we note down the result (like a memo). When we go to compute a value, we first check to see if we have already found it.
To perform memoization for Fibonacci, we can pass an array of int
values of length n + 1. The values in this array all begin with a
value of 0. When computing the Fibonacci value for a particular n,
we first check to see if its value is in the array. If not, we perform
the recursion and store the result in the array.
public static int fibonacci(int n, int[] results) {
if(results[n] == 0) {
if(n == 0 || n == 1)
results[n] = 1;
else
results[n] = fibonacci(n-1) + fibonacci(n-2);
}
return results[n];
}This change makes the computation of the nth Fibonacci number much more efficient; however, even more efficient approaches are described in the exercises.
The famous Tower of Hanoi puzzle is another example commonly used to illustrate recursion. In this puzzle, there are three poles containing a number of different sized disks. The puzzle begins with all disks arranged in a tower on one pole in decreasing size, with the smallest diameter disk on top and the largest on the bottom. Figure 19.5 shows an example of the puzzle. The goal is to move all the disks from the initial pole to the final pole, with two restrictions.
-
Only one disk can be moved at a time.
-
A larger disk can never be placed on top of a smaller disk.

The extra pole is used as a holder for intermediate moves. The idea behind the recursive solution follows.
-
Base Case
Moving one disk is easy. Just move it from the pole it’s on to the destination pole. -
Recursive Case
In order to move n > 1 disks from one pole to another, we can move n - 1 disks to an intermediate pole, move the nth disk to the destination pole, and then move the n - 1 disks from the intermediate pole to the destination pole.
The Tower of Hanoi solution in Java translates this outline into code.
'A', 'B', and 'C'.public class TowerOfHanoi {
public static void main(String[] args) {
move(4, 'A', 'C', 'B');
}
public static void move(int n, char fromPole, char toPole, char viaPole) {
if(n == 1)
System.out.format("Move disk from pole %c to pole %c.\n",
fromPole, toPole);
else {
move(n - 1, fromPole, viaPole, toPole);
move(1, fromPole, toPole, viaPole);
move(n - 1, viaPole, toPole, fromPole);
}
}
}A legend tells of monks that are solving the Tower of Hanoi puzzle with 64 disks. The legend predicts that the world will end when they finish. Run the implementation above with different numbers of disks to see how long the sequence of moves is. Try small numbers of disks, since large numbers of disks take a very long time.
Both Fibonacci and the Tower of Hanoi have natural recursive structures. In the case of Fibonacci, one way to implement its natural recursive definition results in very wasteful computation. In the case of the Tower of Hanoi, the only way to solve the problem takes an excruciatingly long amount of time.
However, we can apply recursion to many practical problems and get efficient solutions. Consider the problem of exponentiation, which looks trivial: Given a rational number a and a positive integer n, find the value of an.
It’s tempting to call Math.pow(a, n) or to use a short for loop to
compute this value, but what if neither tool existed in Java? A simple
recursive formulation can describe exponentiation.

As with factorial and Fibonacci, directly converting the recursive definition into Java syntax yields a method that computes the correct value.
public static double power(double a, int n) {
if(n == 1) // Base case
return a;
else // Recursive case
return a*power(a, n - 1);
}Admittedly, this method only works for positive integer values of
n. Ignoring that limitation, what can we say about its
efficiency? For any legal value of n, the method is called
n times. If n has a small value, like 2 or
3, the process is quick. But if n is 1,000,000 or so, the
method might take a while to finish. Another problem is that stack size
is limited. On most systems, the JVM crashes with a StackOverflowError
if a method tries to call itself recursively 1,000,000 times.
If we limit n to a power of 2, we can do something clever that makes the method much more efficient with many fewer recursive calls. Consider this alternative recursive definition of exponentiation.

Recalling basic rules of exponents, it’s true that an = (an/2)2, but what does that buy us? If we structure our method correctly, we cut the size of n in half at each recursive step instead of only reducing n by 1.
public static double power(double a, int n) {
if(n == 1) // Base case
return a;
else { // Recursive case
double temp = power(a, n/2);
return temp*temp;
}
}Note that we only make the recursive call once and save its result in temp.
If we made two recursive calls, we would no longer be more efficient than
the previous method. That version took n recursive calls.
How efficient is this version? The answer is the number of times you
have to cut n in half before you get 1. Let’s call that
value x. Recall that n is a power of 2,
meaning that n = 2k for some integer
k ≥ 0.

In other words, the number of times you have to divide n
in half to get 1 is the logarithm base 2 of n, written
log2 n. The logarithm function is the inverse of
exponentiation. It cuts any number down to size very quickly (just as
exponentiation blows up the value of a number very quickly). For
example, 220 = 1,048,576. Thus,
log2 1,048,576 = 20. The original version of power()
would have to make 1,048,576 calls to raise a number to that power. This
second version would only have to make 20 calls.
It’s critical that n is a power of 2 (1, 2, 4, 8, …); otherwise, the process of repeatedly cutting n in half loses some data due to integer division. The problem is that, at some point in the recursion, the value of n will become odd unless you start with a power of 2. There’s a way to extend this clever approach to all values of n, even and odd, but we leave it as an exercise.
Recursion offers elegant ways to compute mathematical functions like those we’ve explored in this section. Recursion also offers powerful ways to manipulate data structures. As we show in the next section, recursive methods are especially well suited to use with recursive data structures.
19.4. Syntax: Recursive data structures
Because recursion can be used to do anything that iteration can do, it’s
clear that data structures can be processed recursively. For example,
the following recursive method reverses the contents of an array. It
keeps track of the position it’s swapping in the array with the
position parameter. This method is initially called with a value of
0 passed as an argument for position.
public static void reverse(int[] array, int position) {
if(position < array.length/2) {
int temp = array[position];
array[position] = array[array.length - position - 1];
array[array.length - position - 1] = temp;
reverse(array, position + 1);
}
}Note that nothing is done in the base case for this recursive method.
The recursion swaps the first element of the array (at index 0) with
the last (at index array.length - 1). Recursion continues until
position has reached half the length of array. If execution
continued past the halfway point, it would begin to re-swap elements that
had already been swapped.
Although it’s possible to reverse an array recursively, there’s usually no advantage in doing so. We introduced bubble sort and selection sort in previous chapters, but neither of these algorithms is very fast. Many of the best sorting algorithms are recursive, as in the following example of merge sort.
Merge sort is an efficient sorting algorithm that’s often implemented recursively. The idea of the sort is to break a list of items in half and recursively merge sort each half. Then, these two sorted halves are merged back together into the final sorted list. The base case of the recursion is when there’s only a single item in the list, since a list with only one thing in it is, by definition, sorted.
Here’s a method that recursively sorts an int array using the merge
sort algorithm.
public static void mergeSort(int[] array) {
if(array.length > 1) {
int[] a = new int[array.length/2];
int[] b = new int[array.length - a.length];
for(int i = 0; i < a.length; ++i)
a[i] = array[i];
for(int i = 0; i < b.length; ++i)
b[i] = array[a.length + i];
mergeSort(a);
mergeSort(b);
merge(array, a, b);
}
}The mergeSort() method is quite short and appears to do very little.
It starts by creating arrays a and b and copying roughly half of the
elements in array into each. We make a half the size of array, but
we can’t do the same thing for b because an odd length for array
would leave us without enough space in a and b to hold everything
from array. Instead, we let b hold however much is leftover after
the elements for a have been accounted for.
Then, arrays a and b are recursively sorted. Finally, these two
sorted arrays are merged back into array in sorted order using a
helper method called merge(). This method is non-recursive and does
much of the real work in the algorithm.
public static void merge(int[] array, int[] a, int[] b) {
int aIndex = 0;
int bIndex = 0;
for(int i = 0; i < array.length; ++i) {
if(bIndex >= b.length)
array[i] = a[aIndex++];
else if(aIndex >= a.length)
array[i] = b[bIndex++];
else if(a[aIndex] <= b[bIndex])
array[i] = a[aIndex++];
else
array[i] = b[bIndex++];
}
}The merge() method loops through all the elements in array, filling
them in. We keep two indexes, aIndex and bIndex, that keep track of
our current positions in the a and b arrays, respectively. This
method assumes that a and b are sorted and that the sum of their
lengths is the length of array. We want to compare each element in a
and b, always taking the smaller and putting it into the next
available location in array. Since the next smallest item could be in
either a or b, we never know when we’ll run out of elements in
either array. That’s why the first two if statements in the merge()
method check to see if the bIndex or the aIndex is already past the
last element in its respective array. If so, the next element from the
other array is automatically used. By the time the third if statement
is reached, we’re certain that both indexes are valid and can compare
the elements at those locations to see which is smaller.
Sorting lists using the merge sort algorithm seems more complicated than using bubble sort or selection sort, but this additional complication pays dividends. For large lists, merge sort performs much faster than either of those sorts. In fact, its speed is comparable to the best general sorting algorithms that are possible.
Although recursive sorting algorithms are useful for arrays, recursion
really shines when manipulating recursive data structures. A recursive
data structure is one that’s defined in terms of itself. For example,
class X is recursive if there’s a field inside X with type X.
public class X {
private int a, b;
private X x;
}The linked list examples from
Chapter 18 are recursive
data structures, since a linked list node is defined in terms of itself. You
might not have thought of the linked list Node class as being recursive since
it simply has a reference to another Node inside it. However, this
self-reference is the essence of a recursive data structure.
Data structures are often defined recursively. We typically need to represent an unbounded collection of data, but we always write bounded programs to describe the data. A recursive data structure allows us to bridge the gap between a compile-time, fixed-length definition and a run-time, unbounded collection of objects.
Recursive data structures have a base case to end the recursion.
Typically, the end of the recursion is indicated by a link with a null
value. For example, in the last node of a linked list, the next field is
null. Unsurprisingly, recursive methods are frequently used to
manipulate recursive data structures.
How would you get the size of a linked list? The implementation in
Program 18.5 keeps track of its size as it grows, but
what if it didn’t? A standard way to count the elements in the list
would be to start with a reference to the head of the list and a counter
with value zero. As long as the reference is not null, add one to the
counter and set the reference to the next element on the list.
Program 19.2 counts the elements in this way.
size() method counts its elements iteratively.public class IterativeListSize {
private static class Node {
public String value;
public Node next;
}
private Node head = null;
public void add(String value) {
Node temp = new Node();
temp.value = value;
temp.next = head;
head = temp;
}
public int size() {
Node current = head;
int counter = 0;
while(current != null) {
current = current.next;
counter++;
}
return counter;
}
}An alternative way to count the number of elements in a linked list is
to use the natural recursion of the linked list itself. We can say that
the length of a linked list is 0 if the list is empty (the current link
is null); otherwise, it’s one more than the size of the rest of the
list.
Program 19.3 counts the elements in a linked
list using this recursive procedure. Note that there’s a non-recursive
size() method that calls the recursive size() method. This
non-recursive method is called a proxy method. The recursive method
requires access to the internals of the data structure. The proxy method
calls the recursive method with the appropriate starting point (head),
while providing a public way to get the list’s size without exposing its
internals.
size() method for counting its elements.public class RecursiveListSize {
private static class Node {
public String value;
public Node next;
}
private Node head = null;
public void add(String value) {
Node temp = new Node();
temp.value = value;
temp.next = head;
head = temp;
}
// Proxy method
public int size() {
return size(head);
}
private static int size(Node list) {
if(list == null) // Base case
return 0;
else
return 1 + size(list.next); // Recursive case
}
}19.4.1. Trees
A linked list models a linear, one-to-one relationship between its elements since each item in the list is linked to a maximum of one following item. Another useful relationship to model is a hierarchical, one-to-many relationship: parent to children, boss to employees, directory to files, and so on. These relationships can be modeled using a tree structure, which begins with a single root, and proceeds through branches to the leaves. Typically, the elements of a tree are also called nodes, with the three following special cases.
-
Root node
The root of the tree has no parents. -
Leaf node
A leaf is at the edge of a tree and has no children. -
Interior node
An interior node has a parent and at least one child. It’s neither the root nor a leaf.
Figure 19.6 shows a visualization of a tree. In nature, a tree has its root at the bottom and branches upward. Since the root is the starting point for a tree data structure, it’s almost always drawn at the top.

Abstractly, a tree is either empty (the base case) or contains
references to 0 or more other trees (the recursive case). Trees are
useful for storing and retrieving sorted data efficiently. Some
applications include dictionaries, catalogs, ordered lists, and any
other sorted set of objects. For these purposes, we can define an
abstract data type that includes operations such as add() and
find().
A special case of a tree that’s used frequently is a binary tree, in which each node references at most two other trees.
A binary search tree is a further special case of a binary tree with the following three properties.
-
The value in the left child of the root is smaller than the value in the root.
-
The value in the right child of the root is larger than the value in the root.
-
Both the left and the right subtrees are binary search trees.
This recursive definition describes a tree that makes items with a
natural ordering easy to find. If you’re looking for an item, you first
look at the root of the tree. If the item you want is in the root,
you’ve found it! If the item you want is smaller than the root, go left.
If the item you want is larger than the root, go right. If you ever run
out of tree nodes by hitting a null, the item isn’t in the tree.
This example is a simple binary tree that can store a list of String
values and print them out in alphabetical order. Program 19.4 shows
the Tree class that defines the fields and two public methods, add()
and print(), that operate on the tree. Each is a proxy method that
calls its private recursive version, which takes a reference to a Node
object. The Node static nested class contains three fields.
-
value: theStringvalue stored at the node -
left: a link to the left subtree -
right: a link to the right subtree
Strings values.public class Tree {
private static class Node {
public String value;
public Node left = null;
public Node right = null;
}
private Node root = null;
// Proxy add
public void add(String value) {
root = add(value, root);
}
private static Node add(String value, Node tree) {
if(tree == null) { // Base case (1)
tree = new Node();
tree.value = value;
}
// Left recursive case (2)
else if(value.compareTo(tree.value) < 0)
tree.left = add(value, tree.left);
// Right recursive case (3)
else if(value.compareTo(tree.value) > 0)
tree.right = add(value, tree.right);
return tree; (4)
}
// Proxy print
public void print() {
print(root);
}
private static void print(Node tree) {
if(tree != null) {
print(tree.left); (5)
System.out.println(tree.value); (6)
print(tree.right); (7)
}
}
}| 1 | The recursive add() method first checks to see if the current subtree
is empty (null). If so, it creates a new Node and puts value
inside it. |
| 2 | If the current subtree is not null, it checks to see if
value is smaller or larger than the value at the root of the subtree.
If it’s smaller, it recurses down the left subtree. |
| 3 | If it’s larger, it
recurses down the right subtree. If value is already in the root node,
it does nothing. |
| 4 | Remember that all parameters are pass by value in Java. Thus, assigning
a new Node to tree doesn’t by itself change anything at higher
levels of the tree. What does change the links in the parent of the
current subtree is returning the tree pointer. If the recursive call
to add() was made with a left or a right subtree, the left or
right link, respectively, of the parent Node is assigned the return
value. If the call was made with root, the parent of the entire tree,
the non-recursive add() method sets its value when the recursive
add() returns. |
| 5 | The recursive print() method starts by walking down the left subtree.
Those values are all alphabetically less than the value of the current
node. |
| 6 | When it finishes, it prints the current node value. |
| 7 | Finally, it walks the right subtree to print the values that alphabetically follow the value in the current node. This path through the nodes of the tree is called an inorder traversal. |
Figure 19.7 shows a visualization of the contents of
this implementation of a binary search tree. As with a linked list, an
“X” is used in place of arrows that point to null.

With the power of a binary search tree, it takes virtually no code at
all to store a list of String values and then print them out in sorted
order. Program 19.5 gives an example of this
process using a Tree object for storage.
String values, stores them in a binary search tree, and prints the results in sorted order.import java.util.Scanner;
public class ReadAndSortStrings {
public static void main(String[] args) {
Tree tree = new Tree();
Scanner in = new Scanner(System.in);
while(in.hasNextLine())
tree.add(in.nextLine());
tree.print();
}
}Binary search trees (and other trees, including heaps, tries, B-trees, and more) are fundamental data structures that have been studied heavily. Designing them to have efficient implementations that balance the size of their left and right subtrees is an important topic that’s beyond the scope of this book.
19.4.2. Generic dynamic data structures and recursion
Combining dynamic data structures and generics from the previous chapter and recursion from this chapter gives us the full power of generic dynamic data structures and recursive methods to process them.
Consider Program 19.6, which implements a tree that
stores values of type Integer. Although it would be more efficient to
store int values, we use the Integer wrapper class to ease our
eventual transition into a parameterized generic type.
public class IntegerTree {
private static class Node {
Integer value;
Node left = null;
Node right = null;
}
private Node root = null;
// Proxy add
public void add(Integer value) {
root = add(value, root);
}
private static Node add(Integer value, Node tree) {
if(tree == null) { // Base case
tree = new Node();
tree.value = value;
}
// Left recursive case
else if(value.compareTo(tree.value) < 0)
tree.left = add(value, tree.left);
// Right recursive case
else if(value.compareTo(tree.value) > 0)
tree.right = add(value, tree.right);
return tree;
}
// Proxy print
public void print() {
print(root);
}
private static void print(Node tree) {
if(tree != null) {
print(tree.left);
System.out.println(tree.value);
print(tree.right);
}
}
}It’s a waste to create class IntegerTree, which is identical to
Tree except that the type String has been replaced by Integer. As
in Section 18.5, we want our data
structures, recursive or otherwise, to hold any type. In this way, we
can reuse code across a wide range of applications.
Program 19.7 defines a generic version of the Tree
class. This example is complicated by the fact that we need to be able
to compare the value we want to store with the value in each Node
object. We can’t make a tree with any arbitrary type. Objects of the
type must have the ability to be compared to each other and ordered.
Thus, we use a bounded type parameter specifying that the type T
stored in each Tree must implement the Comparable interface. This
requirement complicates the generic syntax significantly but guarantees
that any type that cannot be compared with itself is rejected at
compile-time.
public class GenericTree<T extends Comparable<T>> {
private class Node {
T value;
Node left = null;
Node right = null;
}
private Node root = null;
// Proxy add
public void add(T value) {
root = add(value, root);
}
private Node add(T value, Node tree) {
if(tree == null) { // Base case
tree = new Node();
tree.value = value;
}
// Left recursive case
else if(value.compareTo(tree.value) < 0)
tree.left = add(value, tree.left);
// Right recursive case
else if(value.compareTo(tree.value) > 0)
tree.right = add(value, tree.right);
return tree;
}
// Proxy print
public void print() {
print(root);
}
private void print(Node tree) {
if(tree != null) {
print(tree.left);
System.out.println(tree.value);
print(tree.right);
}
}
}First, note that the Node class and the recursive methods are no longer
static. The generic syntax for keeping them static without producing
compiler warnings is unnecessarily complex. The type specifier T extends
Comparable<T> guarantees that type T implements the interface
Comparable<T>. The generic Comparable interface defined in the Java API
is as follows.
public interface Comparable<T> {
int compareTo(T object);
}The syntax for generics in Java with type bounds is complicated, and we only scratch the surface here. The good news is that these subtleties are more important for people designing data structures and libraries and come up infrequently for programmers who are only using the libraries.
Program 19.8 uses the generic tree class to
create two kinds of trees, a tree of String objects and a tree of
Integer objects. Java library implementations of binary search trees
are available as the TreeSet and TreeMap classes.
import java.util.Random;
import java.util.Scanner;
public class ReadAndSortGenerics {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
GenericTree<String> stringTree = new GenericTree<>();
GenericTree<Integer> integerTree = new GenericTree<>();
while(in.hasNextLine())
stringTree.add(in.nextLine());
stringTree.print();
Random random = new Random();
for (int i = 0; i < 10; i++)
integerTree.add(random.nextInt());
integerTree.print();
}
}19.5. Solution: Maze of doom
Our algorithm for solving the maze follows the conventional
pencil-and-paper method: trial and error! We mark locations in the maze
with '*' as we explore them. If we come to a dead end, we unmark the
location (by replacing '*' with ' ') and return to our previous
location to try a different direction.
We start at the beginning square of the maze, which must be a passageway.
We mark that location as part of the path by putting '*' in the cell.
Now, what can we do? There are, in general, four possible directions to
head: up, down, left, or right. If that direction doesn’t take us
outside the bounds of the array, then we find either a wall or a
passageway. If we’ve been walking through the maze, we might also find
a part of the current path (often the square we were on before the
current one).
Suppose from our current point in the maze we could send a scout ahead in each of the four directions. If the direction didn’t take the scout out of bounds, he would find either a wall, a part of the current path (the path that led into that space), or an open passageway. If the scout doesn’t find an open passageway, he reports back that that direction doesn’t work.
On the other hand, if the scout finds an open passageway, what does he do? Brace yourself! He does the exact same thing we just did: send out scouts of his own in each of the four possible directions.
With careful, consistent coding, the scout follows the exact same process we did. And the scout’s scouts. And so on. There is, in fact, only one method and instead of calling a scout method to investigate each of the squares in the four directions, we call our own method recursively.
import java.util.Scanner;
public class MazeSolver {
private char[][] maze; (1)
private final int ROWS, COLUMNS; (2)
public static void main(String[] args) {
MazeSolver solver = new MazeSolver(); (3)
if(solver.solve(0, 0))
System.out.println("\nSolved!");
else
System.out.println("\nNot solvable!");
solver.print(); (4)
} | 1 | The MazeSolver class needs a two-dimensional array of char values to
store a representation of the maze. |
| 2 | It’s also convenient to store the number of rows and columns as constant fields. |
| 3 | The main() method creates a new MazeSolver object and then calls its
solve() method with a starting location of (0, 0). It prints an
appropriate message depending on whether or not the maze was solved. |
| 4 | Finally, it prints out the maze, which includes a path marked with '*'
symbols if the maze is solvable. |
public MazeSolver() {
Scanner in = new Scanner(System.in); (1)
ROWS = in.nextInt(); (2)
COLUMNS = in.nextInt();
in.nextLine();
maze = new char[ROWS][COLUMNS]; (3)
for(int row = 0; row < ROWS; row++) { (4)
String line = in.nextLine();
System.out.println(line);
for (int column = 0; column < COLUMNS; column++)
maze[row][column] = line.charAt(column);
}
}| 1 | The constructor for MazeSolver creates a Scanner. It assumes that
the file describing the maze is redirected from standard input, although
it would be easy to modify the constructor to take a file name and read
from there instead. |
| 2 | Next, it reads two integers and sets the ROWS and
COLUMNS to those values, which will be constants moving forward. |
| 3 | It allocates a two-dimensional array of
char values with ROWS rows and COLUMNS columns. |
| 4 | Finally, it reads
through the file, storing each line of char values into this array. As
it reads, it prints out each line to the screen, showing the initial
(unsolved) maze. |
public void print() {
for(int row = 0; row < ROWS; row++) {
for (int column = 0; column < COLUMNS; column++)
System.out.print(maze[row][column]);
System.out.println();
}
}The print() method is a utility method that prints out the maze. It
iterates through each row, printing out the values for the columns in
that row.
public boolean solve(int row, int column) {
if(row < 0 || column < 0 || row >= ROWS || column >= COLUMNS)
return false;
else if(maze[row][column] == 'E')
return true;
else if(maze[row][column] != ' ')
return false;
else {
maze[row][column] = '*';
if(solve(row - 1, column) || solve(row + 1, column) ||
solve(row, column - 1) || solve(row, column + 1))
return true;
else {
maze[row][column] = ' ';
return false;
}
}
}
}The heart of the solution is the recursive method solve(). The
solve() method takes two parameters, row and column, and tries to
find a solution to the maze starting at location maze[row][column]. It
assumes that the maze is filled with '+' for walls, ' ' for
passageways, and may include '*' characters at locations that are part
of the partially completed solution.
If solve() is able to find a solution from the current location, it
returns true, otherwise it returns false. There are three base cases
for the current location in the maze.
-
The current location is outside the maze. Return
false. -
The current location is the ending location (marked with
'E'). We have a winner, returntrue! -
The current location is not a passage (either a wall or a location in the current path that’s already been marked). This call to
solveis not making progress toward the finish. Returnfalse.
If none of the base cases applies, then the current location, which must
contain a ' ' character, might be on a successful path, so solve()
gives it a try. The method tentatively marks the current position with
'*'. Then, it tries to find a path from the current
location to each of the four neighboring cells by recursively calling solve().
If any of those four neighbors returns true, then solve() knows it’s found
a completed path and returns true to its caller.
If none of the four neighbors was on a path to the destination, then the
current location is not on a path. The method unmarks the current
location (by storing a ' ') and returns false. Presumably, its
caller figures out what to do next, perhaps calling a different one of
its neighbors or giving up and returning false to its caller.
The very first call to solve() from the main() method either returns
true if a complete path through the maze is found or false if no
path exists. Note that this solver has no guarantee of finding the
shortest path through the maze, but if there’s at least one path to
the goal, it’ll find one.
19.6. Concurrency: Futures
This section doesn’t deal explicitly with recursion, but it does deal with concurrency and methods in an interesting way. When we call a method in Java, a stack frame for the method is put on the stack, and the thread of execution begins executing code inside the method. When it’s done, it returns a value (or not), and execution resumes in the caller. But what if calling the method began executing an independent thread, and the caller continued on without waiting for the method to return?
This second situation should seem familiar, since it’s exactly what
happens when the start() method is called on a Thread object: the
start() method returns immediately to its caller, but an independent
thread of execution has begun executing the code in the run() method
of the Thread.
What if we only care about the value that’s computed by the new thread of execution? We can think of spawning the thread as an asynchronous method call, a value that’s computed at some point rather than one we have to wait for. The name for such an asynchronous method call is a future. In some languages, particularly functional languages, all concurrency is expressed as a future. In Java, only a little bit of code is needed to create threads that can behave like futures. However, the idea of futures is pervasive enough that Java API tools were created to make the process of creating them simple.
We introduce three interfaces and a factory method call that can allow you to use futures in Java. This section is not a complete introduction to futures, but the tools presented are enough to get you started.
The first interface is the Future interface, which allows you to store
a reference to the asynchronous computation while it’s computing,
before you ask for its value. The second interface is the Callable
interface, which is similar to the Runnable interface in that it
allows you to specify a class whose objects can be started as
independent threads. Both the Future and Callable interfaces are
generic interfaces that require you to specify a type. Remember that futures
are supposed to give back an answer, and that’s the type you supply
as a parameter. For example, when creating a future that returns an
int value, you would create a class that implements the
Callable<Integer> interface, requiring it to contain a method with the
signature Integer call(). Likewise, you would store a reference to the
future you create in a Future<Integer> reference.
And how do you create such a future? Usually, many futures are running
at once to leverage the power of multiple cores. What if you want to
create 100 futures but only have 8 cores? The process of creating
threads is expensive, and it might not be worthwhile to create 100
threads when only 8 are able to run concurrently. To deal with this
problem, the Java API provides classes that implement the
ExecutorService interface, which can maintain a fixed-size pool of
threads. When a thread finishes computing one future, it’s
automatically assigned another. To create an object that can manage
threads this way, call the static factory method newFixedThreadPool()
on the Executors class with the size of the thread pool you want
create. For example, we can create an ExecutorService with a pool of 8
threads as follows.
ExecutorService executor = Executors.newFixedThreadPool(8);Once you have an ExecutorService, you can give it a Callable object
of a particular type (such as Callable<Integer>) as a parameter to its
submit() method, and it will return a Future object of a matching type
(such as Future<Integer>). Then, the future is running (or at least
scheduled to run). At any later point you can call the get() method on
the Future object, which returns the value of its computation. Like
calling join(), calling get() is a blocking call that might have to
wait for the future to finish executing.
All this messy syntax should become clearer in the following example which uses futures to compute the sum of the square roots of the first 100,000,000 integers concurrently.
To use futures to sum the square roots of integers, we first need a
worker class that implements Callable. Since the result of the sum of
square roots is a double, it must implement Callable<Double>. Recall
that primitive types such as double can’t be used as generic type
parameters, requiring us to use wrapper classes in those cases.
import java.util.concurrent.*; (1)
public class RootSummer implements Callable<Double> {
private int min;
private int max;
public RootSummer(int min, int max) { (2)
this.min = min;
this.max = max;
}
public Double call() { (3)
double sum = 0.0;
for(int i = min; i < max; ++i)
sum += Math.sqrt(i);
return sum;
}
}| 1 | First, we import java.util.concurrent.* to have access to the Callable
interface. |
| 2 | RootSummer is a simple worker class that takes a min and a max
value in its constructor. |
| 3 | Its call() method returns the sum of the square roots of all the int
values greater than or equal to min and less than max. |
Of course, we need another class to create the ExecutorService, start
the futures running, and collect the results.
import java.util.concurrent.*; (1)
import java.util.ArrayList;
public class RootFutures {
private static final int THREADS = 10; (2)
private static final int N = 100000000;
private static final int FUTURES = 1000;
public static void main(String[] args) {
ArrayList<Future<Double>> futures = new ArrayList<>(FUTURES); (3)
ExecutorService executor = Executors.newFixedThreadPool(THREADS); (4)
int work = N/FUTURES; (5)| 1 | The first part of RootFutures is setup. The imports give us the
concurrency tools we need and a list to store our futures in. |
| 2 | We have three constants. THREADS specifies the number of threads to
create. N gives the number we’re going up to. FUTURES is the total number
of futures we create, considerably larger than the number of threads
they share. |
| 3 | Inside the main() method, we create an ArrayList to hold the
futures. Since we know the number of futures ahead of time, an array
would be ideal. Unfortunately, quirks in the way Java handles generics
make it illegal to create an array with a generic type. Instead, we
create an ArrayList with the size we’ll need pre-allocated. |
| 4 | Next, we create an ExecutorService with a thread pool of size THREADS. |
| 5 | Finally, we find the amount of work done by each future by dividing N
by FUTURES. We can use simple division in this case instead of a more
complicated load-balancing approach because 100,000,000 is divisible by 10. |
System.out.println("Creating futures...");
for(int i = 0; i < FUTURES; i++) {
Callable<Double> summer = new RootSummer(1 + i*work, 1 + (i + 1)*work); (1)
Future<Double> future = executor.submit(summer); (2)
futures.add(future);
}| 1 | To create the futures, we first instantiate a RootSummer object with the
appropriate bounds for the work it’s going to compute. |
| 2 | Then, we supply that object to the submit() method on the
ExecutorService, which returns a Future object. We could have saved a
line of code by storing this return value
directly into the list futures. |
System.out.println("Getting results from futures...");
double sum = 0.0;
for(Future<Double> future: futures) { (1)
try {
sum += future.get(); (2)
}
catch(InterruptedException | ExecutionException e) { (3)
e.printStackTrace();
}
}
executor.shutdown(); (4)
System.out.println("The sum of square roots is: " + sum); (5)
}
}| 1 | To collect the values from each future, we iterate
through the list of futures with an enhanced for loop. |
| 2 | We add the return value of each future’s get() method to our running
total sum. |
| 3 | Because get() is a blocking call, we have to catch an InterruptedException
in case we’re interrupted while waiting for the future to respond.
However, we also have to catch an ExecutionException in case an
exception occurs during the execution of the future. This exception
handling mechanism is one of the big advantages of using futures:
Exceptions thrown by the future are propagated back to the thread that
gets the answer from the future. Normal threads simply die if they have
unhandled exceptions. Note that we use the modern exception-catching syntax
to handle two unrelated exceptions with the same catch block. |
| 4 | After all the values have been read and summed, we shut the
ExecutorService down. If we’d wanted, we could have submitted
additional Callable objects to it to run more futures. |
| 5 | Finally, we print out the result. |
19.7. Exercises
Conceptual Problems
-
Example 19.1 gave a mathematical recursive definition for x · y. Give a similar recursive definition for x + y, assuming that y is a positive integer. The structure is similar to the recursion to determine your current age given in Section 19.2.1.
-
In principle, every problem that can be solved with an iterative solution can be solved with a recursive one (and vice versa). However, the limited size of the call stack can present problems for recursive solutions with very deep recursion. Why? Conversely, are there any recursive solutions that are impossible to turn into iterative ones?
-
Consider the first (non-memoized) recursive version of the Fibonacci method given in Example 19.5. How many times is
fibonacci()called with argument 1 to computefibonacci(n)? Instrument your program and count the number of calls for n = 2, 3, 4, …, 20. -
In the recursive
solve()method in theMazeSolverprogram given in Section 19.5, the current location in the maze array is set to a space character (' ') if no solution is been found. What value was in that location? How would the program behave if the value wasn’t changed back?
Programming Practice
-
Exercise 8.11 from Chapter 8 challenges you to write a method to determine whether a
Stringis a palindrome. Recall that a palindrome (if punctuation and spaces are ignored) can be described as an emptyStringor aStringin which the first and last characters are equal, with all the characters in between forming a palindrome. Write a recursive method with the following signature to test if aStringis a palindrome.public static boolean isPalindrome(String text, int start, int end)In this method, the
startparameter is the index of the first character you’re examining, and theendparameter is the index immediately after the last character you’re examining. Thus, it would initially be called with aString,0, and the length of theString, as follows.boolean result = isPalindrome("A man, a plan, a canal: Panama", 0, 30); -
The efficient implementation of Fibonacci from Example 19.5 eliminates redundant computation through memoization, storing values in an array as they’re found. However, it’s possible to carry along the computations of the previous two Fibonacci numbers without the overhead of storing an array. Consider the following method signature.
public static int fibonacci(int previous, int current, int n)The next recursive call to the
fibonacci()method passes inn - 1and suitably altered versions ofpreviousandcurrent. Whennreaches0, thecurrentparameter holds the value of the Fibonacci number you were originally looking for.The method would be called as follows for any value of
n.int result = fibonacci(0, 1, n);Complete the implementation of this recursive method.
-
Write an implementation of fast exponentiation that works for even and odd n. This implementation is exactly the same as the one given at the end of Example 19.7 except when n is odd. Use the following recursive definition of exponentiation to guide your implementation.
-
Example 19.5 shows two implementations that can be used to find the nth Fibonacci number. With some knowledge of recurrence relations, it’s possible to show that there’s a closed-form equation that gives the nth Fibonacci number Fn where F0 = F1 = 1.
Although this equation is a bit ugly, you can plug numbers into it to discover the value of Fn quickly, provided that you have an efficient way to raise values to the nth power. Use the recursive algorithm for fast exponentiation from Exercise 19.7 to make an implementation that finds the nth Fibonacci number very quickly.
Note that this approach uses real numbers (including the square root of 5) that need to be represented as
doublevalues. There are exact methods that use fast exponentiation of integer matrices to do this computation without doing any floating-point arithmetic, but we won’t go into those details here. -
Example 19.9 shows a way to calculate the size of a linked list recursively. Add a recursive method called
print()to theRecursiveListSizeclass that prints out the values in the linked list recursively, one value per line. -
Expand the previous exercise to add another method called
reversePrint()that prints out the values in the linked list in the opposite order that they appear. It should take only a slight modification of theprint()method you’ve already written. -
Create a recursive
find()method (and a non-recursive proxy method to call it) for theTreeclass given in Program 19.4. Its operation is similar to theadd()method. If the subtree it’s examining is empty (null), it should returnfalse. If the value it’s looking for is at the root of the current subtree, it should returntrue. These are the two base cases. If the value it’s looking for comes earlier in the alphabet than the value at the root of the current subtree, it should look in the left subtree. If the value it’s looking for comes later in the alphabet than the value at the root of the current subtree, it should look in the right subtree. Those are the two recursive cases. -
The height of a binary tree is defined as the longest path from the root to any leaf node. Thus, the height of a tree with only a root node in it is 0. By convention, the height of an empty tree is -1.
Create a recursive
getHeight()method (and a non-recursive proxy method to call it) for theTreeclass given in Program 19.4. The base case is an empty tree (anullpointer), which has a height of -1. For the recursive case of a non-empty tree, its height is one more than the height of the larger of its two subtrees. -
Create a Java interface that describes a tree ADT. Modify the programs in Example 19.10 to implement this interface.
Experiments
-
Write an iterative version of the factorial function and compare its speed to the recursive version given in the text. Use the
System.nanoTime()method before and afterforloops that call the factorial methods 1,000,000 times each for random values. -
Write a program that generates four arrays of random
intvalues with lengths 1,000, 10,000, 100,000, and 1,000,000. Make two additional copies of each array. Then, sort each of three copies of the array with the selection sort algorithm given in Example 6.2, the bubble sort algorithm given in Section 10.1, and the merge sort algorithm given in Example 19.8, respectively. Use theSystem.nanoTime()method to time each of the sorts. Note that both selection sort and bubble sort might take quite a while to sort an array of 1,000,000 elements.Run the program several times and find average values for each algorithm on each array size. Plot those times on a graph. The times needed to run selection sort and bubble sort should increase quadratically, but the time to run merge sort should increase linearithmically. In other words, an array length of n should take time proportional to n2 (multiplied by some constant) for selection sort and bubble sort, but it should take time proportional to n log2 n (multiplied by some constant) for merge sort. For large arrays, the difference in time is significant.
-
Investigate the performance of using recursion to compute Fibonacci numbers. Implement the naive recursive solution, the memoization method, and an iterative solution similar to the memoization method. Use the
System.nanoTime()method to time the computations for large values of n.Warning: It might take a very long time to compute the nth Fibonacci number with the naive recursive solution.
-
Exercise 6.9 from Chapter 6 explains how binary search can be used to search for a value in a sorted array of values. The idea is to play a “high-low” game, first looking at the middle value. If the value is the one you’re looking for, you’re done. If it’s too high, look in the lower half of the array. If it’s too low, look in the upper half of the array. Implement binary search both iteratively and recursively. Populate an array with 100,000
intvalues between 1 and 10,000,000 and sort it. Then, search for 1,000,000 random values generated between 1 and 10,000,000 using iterative binary search and then recursive binary search. Use theSystem.nanoTime()method to time each process. Was the iterative or recursive approach faster? By how much?
20. File I/O
Kira: What are those funny marks?
Jen: This is all writing.
Kira: What’s writing?
Jen: Words that stay, my master said.
20.1. Problem: A picture is worth 1,000 bytes
If you’re familiar with bitmap (bmp) files, you know that they can take
up a lot of space compared to other popular image formats. People often use
a technique called data compression to reduce the size of large files for
storage. There are many different kinds of compression and many which are
tailored to work well on images. Your task is to write a program that will
do a particular kind of compression called run length encoding (RLE), which
we’ll test on bitmaps. The idea behind RLE is simple: Imagine a file as a
stream of bytes. As you look through the stream, replace repeating sequences
of a single byte with a count telling how many times it repeats followed by
the byte that repeats. Consider the following sequence.
215 7 7 7 7 7 7 7 7 7 123 94 94 94 71
Its RLE compressed version could be shown as follows.
1 215 9 7 1 123 3 94 1 71
Since there’s no simple way to keep track of which numbers are counts and which ones are actual bytes of data, we have to keep a count for every byte, even unrepeated ones. In this example, we went from 15 down to 10 numbers, a savings of a third. In the worst case, a file that has no repetition at all would actually double in size after being “compressed” with this kind of RLE. Nevertheless, RLE compression is used in practice and performs well in some situations.
Your job is to write a Java program that takes two arguments from the
command line. The first is either -c for compress or -d for
decompress. The second argument is the name of the file to be compressed
or decompressed. When compressing, append the suffix .compress to the
end of the file name. When decompressing, remove that suffix.
Executing the following on the command line should generate an RLE compressed
file called test.bmp.compress.
java BitmapCompression -c test.bmp
Likewise, executing the following should create an uncompressed file called
test.bmp.
java BitmapCompression -d test.bmp.compress
Be sure to make a backup of the original file (in this case test.bmp) because
decompressing will overwrite a file of the same name.
To perform the compression, go byte by byte through the file. For each
repeating sequence of a byte (which can be as short as a single byte
long), write the length of the sequence as a byte and then the byte
itself into the compressed file. If a repeating sequence is more than
127 bytes, you break the sequence into more than one piece since
the largest value the byte data type can hold in Java is 127. (The
byte type in Java is always signed, giving a range of -128 to 127.)
Decompression simply reads the count then the byte value and writes the
appropriate number of copies of the byte value into the decompressed
file.
20.1.1. Command-line arguments
You might be wondering how to read the command-line arguments such as
-c test.bmp or -d test.bmp.compress. These arguments can’t be read
using Scanner as we read most text. Instead, they’re passed directly into
your program. By this point, you’ve written so many main() methods that you
might have stopped paying attention to their syntax. Remember that main()
methods always take a single parameter of type String[]. We’ve always called
this parameter args in this book, but you’re free to call it whatever you
like.
This array of String values is how command-line arguments are passed into
your program. A Java program invoked by typing
java BitmapCompression -c test.bmp will have an array of length 2 passed in.
The first String stored in this array (args[0]) will be "-c". The second
String stored in this array (args[1]) will be "test.bmp". The operating
system passes in these command-line arguments to the JVM which passes them along
to your program as String values.
Command-line programs often take these arguments to specify which options the
program will be run with. Although they’re useful, we didn’t focus on these
arguments in early chapters partly because they involve arrays and partly because
all arguments, even those that look like numbers, will be passed in as String
values. Furthermore, it’s cumbersome to specify command-line arguments when
using IDEs like Eclipse or IntelliJ.
20.2. Concepts: File I/O
Before you can tackle the problem of compressing, or even reading from and writing to, files, some background on files is necessary. By now, you’ve had many experiences with files: editing Java source files, compiling those files, and running them on a virtual machine, at the very least. You’ve probably done some word processing, looked at photos, listened to music, and watched videos, all on a computer. Each of these activities centers on one or more files. In order to reach these files, you probably had to look through some directories, which are a special kind of file as well. But what is a file?
20.2.1. Non-volatile storage
A computer program is like a living thing, always moving and restless. The variables in a program are stored in RAM, which is volatile storage. The data in volatile memory will only persist as long as there’s electricity powering it. But most programs don’t run constantly, and neither do most computers. We need a place to store data between runs of a particular program. Likewise, we need a place to store data when our computer isn’t turned on. Both scenarios share a common solution: secondary storage such as hard drives, flash drives, and optical media like DVD and Blu-ray discs.
Files are not always stored in non-volatile memory. It’s possible to load entire files into RAM and keep them there for long periods of time. Likewise, all input and output on Unix and Linux systems are viewed as file operations. Nevertheless, the characteristics of non-volatile memory are often associated with file I/O: slow access times and the possibility of errors in the event of inaccessible files or hardware problems.
20.2.2. Stream model
While discussing RLE encoding, we described a file as a stream of bytes, and that’s a good definition for a file, especially in Java. Since Java is platform independent, and different operating systems and hardware will deal with the nitty gritty details of storing files in different ways, we want to think about files as abstractly as possible. Reading from and writing to a stream of bytes is not so different from the other input and output you’ve done so far. For the most part, file I/O will be similar to command-line I/O and, in fact, can use some of the same classes.
Although reading and writing from the files can be like reading from the
keyboard and writing to the screen, there are a few additional complications.
For one thing, you must open a file before you
can read or write. Sometimes opening the file will fail: You could try
to open a file for reading which doesn’t exist or try to open a file
for writing which you don’t have permissions for. When reading data,
you might try to read past the end of the file or try to read an int
when the next item is a String. Unlike reading from the keyboard, you
cannot ask the user to try again if there’s a mistake in input. To deal
with these possible errors, exception handling will accompany many
different file I/O operations in Java.
20.2.3. Text files and binary files
When talking about files, many people divide files into two categories: text files and binary files. A text file can be read by humans. That is, when you open a text file with a simple file reader, it won’t be filled with gibberish and nonsense characters. A Java source file is an excellent example of a text file.
In contrast, a binary file is a file meant only to be read by a computer. Instead of printing out characters meant to be read by a human, the raw bytes of memory for specific pieces of data are written to binary files. To clarify, if we wanted to write the number 2,127,480,645 in a text file, the file would contain the following.
2127480645
However, if we wanted to write the same number in a binary file, the file would contain the following.
~ÎÇE
If you recall, an int in Java uses four bytes of storage. There’s a
system of encoding called the ASCII table which maps each of the 256
(0–255) numerical bytes to a character. The four characters given above
are the extended ASCII representation of the four bytes of the number
2,127,480,645.
In some sense, the idea of a text file is artificial. All files are binary in the sense that they’re readable by a computer. You’ll take different steps and create different objects depending on whether you want to do file I/O in the text or binary paradigms, but the overall process will be similar in either case.
20.3. Syntax: File operations in Java
20.3.1. The File class
A basic class for interacting with files in Java is the File class. A File
object allows you to interact with a file at the operating system level. You
can create a new file, test to see if a file is a directory, find out the size
of a file, and so on. A number of file I/O classes
require a File object as a parameter. To use the File class, import
java.io.File or java.io.*.
To create a File object, you can call the File constructor with a
String specifying the name of the file.
File file = new File("file.txt");Doing so will create a virtual file object associated with the name
file.txt (which might not exist yet) in the working directory of the
Java program. In this case, the extension txt doesn’t have any real
meaning. On many systems, the extension (like pdf or html) is used
by the operating system to guess which application should open the file.
To Java, however, the extension is just part of the file name. A file
name passed to the constructor of a File object can have any number of
periods in it (or none).
A file name without a directory is all well and good, but file systems are
useful in part because of their hierarchical structure. If we want to create a
file in a particular location, we specify the path in the String
before the name of the file.
File file = new File("/homes/owilde/documents/file.txt");In this case, the prefix /homes/owilde/documents/ is the path and
file.txt is still the file name. Each slash ('/') separates a
parent directory from the files or directories inside of it. This path
specifies that we start at the root, go into the homes directory, then
the owilde directory, and then the documents directory. Note that we
can also use a single period (.) in a path to refer to the current
working directory and two periods (..) to refer to a parent directory.
This is one of those sticky places where Java’s trying to be platform
independent, but the platforms each have different needs. The example we
gave above is for a macOS or Linux system. In Windows, the way to specify
the path is slightly different. Creating a similar File object on
Windows system might be done as follows.
File file = new File("C:\\Users\\owilde\\Documents\\file.txt");Then, the path specifies that we start in the C drive, go into the
Users directory, the owilde directory, and then the Documents directory.
Windows systems use a backslash (\) to separate a parent directory from its
children. But in Java a backslash isn’t allowed to be by itself in a
string literal, and so each backslash must be escaped with another
backslash. To simplify things somewhat, Java allows Windows paths to be
separated with regular slashes as well, so we’ll use this style for
the rest of the book.
A further complication is that file and directory names are case sensitive in Linux, aren’t case sensitive in Windows, and could be either in macOS depending on file system settings.
Returning to File objects, there are a number of things we
can do directly. A File object has methods that can test if a file
with the associated name and path exists, if it’s readable, if it’s
writable, and many other things. Because there are so many classes
associated with file I/O and each class has so many methods, now’s a
good time to remind you of the usefulness of the Java API. If you visit
the Java API documentation site,
you can get detailed documentation for the entire standard library, including
file I/O classes.
20.3.2. Reading and writing text files
Once you have a File object, most of its usefulness comes from combining
it with other classes. You’re already familiar with the Scanner
class. The Scanner constructor can take a File object (instead of
System.in), creating a Scanner that reads from a text file instead of the
keyboard.
Scanner in = null;
try {
in = new Scanner(file);
while(in.hasNextInt())
process(in.nextInt());
}
catch(FileNotFoundException e) {
System.out.println("File " + file.getName() + " not found!");
}
finally { if(in != null) in.close(); }Assuming that file is linked to a file which the program has read
access to, this block of code will extract int values from the file
and pass them to the process() method. If the file doesn’t exist or
isn’t readable to the program, a FileNotFoundException will be thrown
and an error message printed. Creating a Scanner from a File object
instead of System.in can throw a checked exception, so the try and catch
are needed before the program will compile. Note that you’ll need to import
java.util.Scanner or java.util.* just like any other time you use the
Scanner class.
And that’s all there is to it. After opening the file, using the
Scanner class will be almost the same as before. One difference is
that you should close the Scanner object (and by extension the file)
when you’re done reading from it, as we do in the example. Closing
files is key to writing robust code.
You’ll notice that we put
in.close() in a finally block. Using finally is a good habit for
file I/O. File operations could fail for any number of reasons, but you
will still need to close the file afterward. We put in the null check
in case the file didn’t exist and the reference in never pointed to a
valid object. (We also begin by setting in to null. Otherwise, Java
complains that it might not have been initialized.)
Writing information to a file is similar to using System.out. First,
you need to create a PrintWriter object. Like Scanner, you can
create a PrintWriter object directly from a File object. If we want to
write a list of random numbers to the file we were reading from earlier,
we could do it as follows.
PrintWriter out = null;
try {
out = new PrintWriter(file);
Random random = new Random();
for(int i = 0; i < 100; ++i)
out.println(random.nextInt());
}
catch(FileNotFoundException e) {
System.out.println("File " + file.getName() + " not found!");
}
finally { if(out != null) out.close(); }Again, once you have a PrintWriter object, the methods for outputting
data are just like using System.out. Be sure to import java.io.* in order
to have access to the PrintWriter class.
20.3.3. Reading and writing binary files
We covered text files first because their input and output is similar to command-line I/O. When reading and writing text files, you can visually verify that file reading and writing operations were successful. Although it’s harder to check the contents of binary files, they have other advantages. Data can often be stored more compactly in binary files, as in the example with the integer 2,127,480,645. Even better, Java provides facilities for easily dumping (and later retrieving) primitive data types, objects, and even complex data structures to binary files.
The simplest object for reading input from a binary file is a
FileInputStream object. As with a File object, you can create a
FileInputStream object from a String specifying the file path and name.
FileInputStream in = new FileInputStream("file.bin");Unfortunately, you can’t do much with a FileInputStream object.
Its methods allow you to read single bytes, either one at a time or into an
array as a group. The basic read() method returns the next byte in the file
or a -1 if the end of the file has been reached. Working only at the level of
bytes, we can still write useful code like the following method that prints the
size of a file.
public static void printFileSize(String fileName) {
FileInputStream in = null;
try {
in = new FileInputStream(fileName);
int count = 0;
while(in.read() != -1)
count++;
System.out.println("File size: " + count + " bytes");
}
catch(Exception e) {
System.out.println("File access failed.");
}
finally { try{ in.close(); } catch(Exception e){} }
}Note the extra try-catch block inside of the finally. Like the
other binary file I/O objects we’ll discuss in this section,
FileInputStream can throw an IOException when closing. Usually, you
won’t need to deal with this exception, but you still must catch it.
Since we’re catching any Exception, we’re saving a little bit of code by
eliminating the null check. If in is null in this example, a
NullPointerException will be thrown and immediately caught, causing no
damage. Catching Exception breaks our rule of never catching exceptions
that are broader than we need, but we only have a single line of code
in our try block with nothing else to do if it fails.
To output a sequence of bytes, you can create a FileOutputStream object.
Its write() methods are the mirror images of the read() methods in
FileInputStream. It would be convenient if there was a way to read
and write any primitive type instead of just byte values, and
DataInputStream and DataOutputStream provide exactly that functionality.
For output, a DataOutputStream chops up primitive data types into their
component bytes and sends those bytes to a FileOutputStream. For input, a
DataInputStream reads a sequence of bytes from a FileInputStream and
reassembles them into whatever kind of primitive data they’re supposed to be.
To create an DataInputStream, you supply a FileInputStream to its
constructor, usually one that you’ve just created on the fly for this purpose.
DataInputStream in = new DataInputStream(new FileInputStream("baseball.bin"));Now, let’s assume that baseball.bin contains baseball statistics. The
first thing in the file is an int indicating the number of records it
contains. Then, for each record, it’ll list home runs, RBI, and
batting average, as an int, an int, and a double, respectively.
Assuming that we’ve opened the file correctly above, we can read these
statistics into three arrays with the following code.
DataInputStream in = null;
try {
in = new DataInputStream(new FileInputStream("baseball.bin"));
int records = in.readInt();
int[] homeRuns = new int[records];
int[] RBI = new int[records];
double[] battingAverage = new double[records];
for(int i = 0; i < records; ++i) {
homeRuns[i] = in.readInt();
RBI[i] = in.readInt();
battingAverage[i] = in.readDouble();
}
}
catch(IOException e) {
System.out.println("File reading failed.");
}
finally { try{ out.close(); } catch(Exception e){} }When opening the file in the FileInputStream constructor, a
FileNotFoundException will be thrown if the file doesn’t exist or is
inaccessible. If the readInt() or readDouble() methods fail, they’ll throw
an IOException. If the DataInputStream object tries to read past the end
of a file, it’ll throw an EOFException exception. If you wanted to deal with
these exceptions separately, you could, but since FileNotFoundException and
EOFException are both children of IOException, a single catch clause
for IOException handles all three.
As expected, the
DataOutputStream methods for writing to a file match DataInputStream
methods for reading from a file. If you substitute write for read,
DataOutputStream methods are almost the same as
DataInputStream methods. Below is a companion piece of code which
assumes that homeRuns, RBI, and battingAverage are filled with
data and writes them to a file.
DataOutputStream out = null;
try {
out = new DataOutputStream(new FileOutputStream("baseball.bin"));
out.writeInt(homeRuns.length);
for(int i = 0; i < homeRuns.length; ++i) {
out.writeInt(homeRuns[i]);
out.writeInt(RBI[i]);
out.writeDouble(battingAverage[i]);
}
}
catch(IOException e) {
System.out.println("File writing failed.");
}
finally { try{ out.close(); } catch(Exception e){} }Using DataInputStream and DataOutputStream in this way isn’t
too difficult, but it seems cumbersome. The programmer has the responsibility
to read and write every piece of primitive data separately. It would be
convenient if there was a way to read an entire object at once, including any
references to other objects that it contains. If a tool exists for reading
an entire object, we’d also want a matching tool for writing an entire
object at once.
Such tools can be found in the ObjectInputStream and
ObjectOutputStream classes, respectively. These file I/O objects provide
methods that elegantly allow you to read or write a whole object at a time. To
use them with our baseball data example, we need to define a new class.
import java.io.Serializable;
public class BaseballPlayer implements Serializable {
private int homeRuns;
private int RBI;
private double battingAverage;
public BaseballPlayer(int homeRuns, int RBI, double battingAverage) {
this.homeRuns = homeRuns;
this.RBI = RBI;
this.battingAverage = battingAverage;
}
public int getHomeRuns() { return homeRuns; }
public int getRBI() { return RBI; }
public double getBattingAverage() { return battingAverage; }
}The new class BaseballPlayer encapsulates the three pieces of
information we want. Note that it also implements the interface
Serializable, but it doesn’t seem to implement any special methods to
conform to the interface. We’ll discuss this interface more after we show how
using this new class can simplify file I/O. Our input code will change to
the following.
ObjectInputStream in = null;
try {
in = new ObjectInputStream(new FileInputStream("baseball.bin"));
int records = in.readInt();
BaseballPlayer[] players = new BaseballPlayer[records];
for(int i = 0; i < players.length; ++i)
players[i] = (BaseballPlayer)in.readObject();
}
catch(IOException e) {
System.out.println("File reading failed.");
}
finally { try{ in.close(); } catch(Exception e){} }The corresponding output will become what follows.
ObjectOutputStream out = null;
try {
out = new ObjectOutputStream(new FileOutputStream("baseball.bin"));
out.writeInt(players.length);
for(int i = 0; i < players.length; ++i)
out.writeObject(players[i]);
}
catch(IOException e) {
System.out.println("File writing failed.");
}
finally { try{ out.close(); } catch(Exception e){} }This process of outputting an entire object at a time is called
serialization. The BaseballPlayer class is very simple, but even
complex objects can be serialized, and Java takes care of almost
everything for you. The only magic needed is for the class that’s
going to be serialized to implement Serializable. There are no methods
in Serializable. It’s just a tag for a class that can be packed up
and stored. The catch is that, if there are any references to other
objects inside of the object being serialized, they must also be
serializable. Otherwise, a NotSerializableException will be thrown
when the JVM tries to perform the serialized output. Many classes are
serializable, including the vast majority of the Java API.
However, objects that have some kind of special system-dependent state,
like a Thread or a FileInputStream object, can’t be serialized. If you
need to serialize a class with references to objects like these, add the
transient keyword to the declaration of each unserializable reference. That
said, these should be few and far between. For BaseballPlayer, adding
implements Serializable was all we needed, and we can still get
more mileage out of serialization! An array can be treated liked an
Object and is also serializable. We can further simplify the input as
shown below.
ObjectInputStream in = null;
try {
in = new ObjectInputStream(new FileInputStream("baseball.bin"));
BaseballPlayer[] players = (BaseballPlayer[])in.readObject();
}
catch(IOException e) {
System.out.println("File reading failed.");
}
finally { try{ in.close(); } catch(Exception e){} }And the corresponding output code can be simplified as well.
ObjectOutputStream out = null;
try {
out = new ObjectOutputStream(new FileOutputStream("baseball.bin"));
out.writeObject(players);
}
catch(IOException e) {
System.out.println("File writing failed.");
}
finally { try{ out.close(); } catch(Exception e){} }When you go to write your code, which binary file I/O classes should you use?
It depends on the situation. FileInputStream and FileOutputStream are very
low level. You’ll use those classes to construct DataInputStream,
DataOutputStream, ObjectInputStream, and ObjectOutputStream objects, but
you probably won’t use them on their own unless your application is focused on
byte-level input and output.
If you only want to read and write primitive types, you can use
DataInputStream and DataOutputStream objects. These classes have methods
to read and write all primitive types. Ultimately, all objects are made up of
primitive types, though those primitive types might be buried inside of other
objects. Most languages provide binary I/O tools like DataInputStream and
DataOutputStream, so code using these objects will be similar to code in other
languages that writes individual pieces of primitive data.
Finally, if you want to read and write whole objects (or even arrays of objects)
at a time, ObjectInputStream and ObjectOutputStream are powerful tools.
Using them leverages Java serialization, making the JVM do the work of dividing
up your objects into primitive types and writing them (for output) or
reading that primitive data and reassembling it into objects (for input). Even
complex objects with many (potentially circular) references to other objects,
like linked list classes, can be serialized. The Java implementation of
serialization is smart enough to write each unique object only once and then
refer to it later. This power feels like magic, but serialization has
limitations. Only classes that implement the Serializable interface can
be serialized. Also, serialization carries with it some overhead: the files
must contain additional metadata describing the class being stored. Using
DataInputStream and DataOutputStream can allow you to write only the
necessary member data, resulting in a smaller file. You can also run into
trouble if you make changes to a class. If one version of an object is
serialized and then you try to read that object back after making the smallest
change to the class, your code will fail. One last issue is that Java
serializes objects according to its own rules, making files written in this
way difficult (if not impossible) to use with code written in other languages.
This consideration is not insignificant, since files are often written by one
program and read by another.
The following table summarizes the three approaches to binary I/O we’ve discussed. Be sure to consult each class’s documentation for more information.
| Class | Use | Purpose | Limitations |
|---|---|---|---|
|
Input |
Simplest binary I/O |
Can only read and write |
|
Output |
||
|
Input |
Binary I/O for primitive types |
Can’t read and write whole objects |
|
Output |
||
|
Input |
Powerful binary I/O for all types |
Depends on Java serialization and can’t work with files created in other ways |
|
Output |
20.3.4. Using JFileChooser
One of the more tedious aspects of working with files in command-line programs
is typing the name of the file correctly. Although most OS terminals have
time-saving autocomplete features to help users choose the right file name,
typing the name of a file directly into a prompt so that it can be read by
a Scanner object is error prone. Navigating long directory paths can also
be a headache when using a command-line interface.
Indeed, most users are used to selecting files to open or to save via a GUI
file chooser instead of typing file names explicitly. The Java Swing library
provides such a file chooser called JFileChooser.
We discussed fully featured GUI programs in Chapter 15, but like the
JOptionPane class covered in Chapter 7,
JFileChooser can be used with or without a complex GUI.
Unlike the JOptionPane class whose functionality is accessed through static
methods, you must create a JFileChooser object to use it.
JFileChooser chooser = new JFileChooser();Once you’ve created the JFileChooser object, you can call either the
showOpenDialog() method to show a dialog to open existing files or the
showSaveDialog() to save a potentially new file. The dialog looks similar
in either case, with only minor differences such as title and buttons names.
int result = chooser.showOpenDialog(null);Both methods take a Component object as an argument. If you’re creating a
GUI program, you can pass in a JFrame or a JDialog for this argument to pop
up a modal file chooser dialog that must be dealt with before returning control
to the parent frame or dialog. If your program doesn’t otherwise use a GUI,
you can pass in null.
Both methods also return an int value indicating the result of user input.
A return value of JFileChooser.APPROVE_OPTION means that the user selected a
file. The value JFileChooser.CANCEL_OPTION means that the user canceled
instead of picking a file. Finally, JFileChooser.ERROR_OPTION means some
error occurred.
Once the user has selected a file for opening or for saving, you can call the
getSelectedFile() method to retrieve the File that the user selected.
File file = chooser.getSelectedFile();If the user canceled or an error occurred, this File object could be null.
In many cases, a programmer will want to focus the user on files of a certain
kind. For example, a program that plays audio files might display only
files that have extensions associated with audio formats such as wav, mp3,
and flac. To include this functionality, you can create a
FileNameExtensionFilter object and set it as a file filter on your
JFileChooser.
FileNameExtensionFilter filter = new FileNameExtensionFilter("Audio", "wav", "mp3", "flac");
chooser.setFileFilter(filter);The first argument to the FileNameExtensionFilter constructor is a
user-friendly description of the kinds of files displayed by the filter. After
the description, the constructor takes a variable number of arguments, each of
which gives one of the included file extensions. Extensions are case
insensitive and should not include a dot (.) at the beginning. You should set
the file filter before displaying a dialog with either showOpenDialog() or
showSaveDialog().
FileNameExtensionFilter covers most of what people want from a file filter,
but it’s possible to create your own class that extends FileFilter if you
need to filter files based on more complex criteria.
Next, we’ll give a short example that uses a JFileChooser.
JFileChooserThe short program below allows a user to select a file using
JFileChooser. Only image files with jpg or png extensions will be
displayed. Once the file has been selected, the program will print out the
number of bytes of storage that the file uses.
JFileChooser.import javax.swing.JFileChooser; (1)
import javax.swing.filechooser.FileNameExtensionFilter;
import java.io.File;
public class FileChooserExample {
public static void main(String[] args) {
JFileChooser chooser = new JFileChooser(); (2)
FileNameExtensionFilter filter = new FileNameExtensionFilter("Images", "jpg", "png");
chooser.setFileFilter(filter); (3)
int result = chooser.showOpenDialog(null); (4)
if(result == JFileChooser.APPROVE_OPTION) { (5)
File file = chooser.getSelectedFile();
if(file != null && file.exists()) { (6)
long size = file.length();
System.out.println("The file contains " + size + " bytes.");
}
else
System.out.println("The file doesn't exist.");
}
else
System.out.println("The user probably canceled.");
}
}| 1 | Imports are needed for the JFileChooser, the FileNameExtensionFilter,
and the File object itself. |
| 2 | First, we create the JFileChooser object. |
| 3 | Next, we create and then set a file filter appropriate for image files. |
| 4 | We show the open dialog to allow the user to select a file. |
| 5 | If the user selected a file rather than canceling, we get the File
object from the file chooser. |
| 6 | If the file exists, we get its length in bytes and print that out. |
If the file didn’t exist or the user hit cancel, we print appropriate messages in those cases as well.
Figure 20.1 shows the dialog displayed by this program.
JFileChooser showing an open dialog.Note that the purpose of JFileChooser is to allow users to select a file. It
doesn’t guarantee that the file exists or that the user has rights to read
from the file or to write to it. Most commercial software asks the user if
he or she wants to overwrite an existing file when saving. JFileChooser
doesn’t have that functionality built in, requiring additional program logic to
to prompt the user if an existing file is about to be overwritten.
Like most of the Swing library, JFileChooser has many options and features
that we don’t have time to cover. Its display can be customized, and it can be
configured to interact with the file system in a number of ways, such as
displaying only normal files, displaying only directories, or both. There are
even settings that allow the user to select multiple files at once.
20.4. Examples: File examples
Let’s return to the File class and look at another example of how to
use it. It’s often useful to know the contents of a directory. At the
Windows command prompt, this is usually done using the dir command; in
Linux and macOS, the ls command is generally used. In a few lines of
code, we can write a directory listing tool which lists all the files in
a directory, the date each file was last modified, and whether or not a file
is a directory.
import java.io.*;
import java.text.*;
import java.util.*;
public class Directory {
public static void main(String[] args) {
File directory = new File("."); (1)
File[] files = directory.listFiles(); (2)
for(File file: files) {
System.out.print(DateFormat.getDateInstance().format(
new Date(file.lastModified())) + "\t"); (3)
if(file.isDirectory()) (4)
System.out.print("directory");
else
System.out.print("\t");
System.out.println("\t" + file.getName()); (5)
}
}
}| 1 | The code first creates a File object using "." to
specify the current working directory. |
| 2 | The listFiles() method returns an array of File objects which we then
iterate over. |
| 3 | We call
lastModified() on each file to get its date, |
| 4 | isDirectory() to see if it’s a directory, |
| 5 | and finally print the name given by getName(). |
The output for this program might look like the following.
Aug 5, 2019 AreaFromRadiusBinary.java Aug 1, 2019 AreaFromRadiusText.java Aug 5, 2019 BaseballPlayer.java Aug 5, 2019 BitmapCompression.java Aug 5, 2019 ConcurrentFileAccess.java Aug 8, 2019 Directory.class Aug 8, 2019 Directory.java Aug 1, 2019 FileChooserExample.java Aug 8, 2019 directory Images Aug 5, 2019 areas.bin Aug 5, 2019 areas.txt Aug 5, 2019 radiuses.bin Aug 5, 2019 radiuses.txt
Now, let’s look at a data processing application of files. Let’s assume
that there’s a file called radiuses.txt which holds the radiuses of a
number of circles formatted as text, one on each line of the file. It’s
our job to read each radius r, compute the areas of each circle using the
formula Area = πr2, and write those areas to a file called areas.txt.
import java.io.*;
import java.util.*;
public class AreaFromRadiusText {
public static void main(String[] args) {
File inFile = new File("radiuses.txt");
File outFile = new File("areas.txt");
Scanner in = null;
PrintWriter out = null;
try {
in = new Scanner(inFile); (1)
out = new PrintWriter(outFile); (2)
while(in.hasNextDouble()) { (3)
double radius = in.nextDouble(); (4)
out.format("%.3f%n", Math.PI*radius*radius); (5)
}
}
catch(FileNotFoundException e) { (6)
System.out.println(e.getMessage());
}
finally { (7)
if(in != null) in.close();
if(out != null) out.close();
}
}
}| 1 | First, we create a Scanner to read text from a file. |
| 2 | Next, we create a PrintWriter to write text to a file. |
| 3 | We continue reading as long as there’s another piece of text formatted
as a legal double. |
| 4 | We read in the double, just as we would from a user typing on the
keyboard. |
| 5 | We use the format() method to print out a double formatted with exactly
three digits after the decimal point followed by a newline, just as we’ve used
System.out.format() in the past. |
| 6 | As is typical with file I/O, we have to catch exceptions. A
FileNotFoundException would have been thrown if either file was inaccessible. |
| 7 | In the finally block, we close both files. It’s vitally important to
close output files to ensure that all their data is actually written to disk. |
Perhaps the input file radiuses.txt contains the following 10 values.
33.675 4.156 8.608 60.350 86.501 78.581 23.935 2.263 26.827 73.358
Then, the output file areas.txt would be filled with these corresponding
10 values. Note that formatting the output to have three digits after the
decimal point is easier to read, but it loses some precision.
3562.584 54.263 232.785 11442.065 23506.725 19399.252 1799.769 16.089 2260.966 16906.155
The previous class did all of its input and output with text files. We’ll
also implement this program to read from a binary file called radiuses.bin
and write to a binary file called areas.bin.
import java.io.*;
public class AreaFromRadiusBinary {
public static void main(String[] args) {
File inFile = new File("radiuses.bin");
File outFile = new File("areas.bin");
DataInputStream in = null;
DataOutputStream out = null;
try {
in = new DataInputStream(new FileInputStream(inFile)); (1)
out = new DataOutputStream(new FileOutputStream(outFile)); (2)
while(true) { (3)
double radius = in.readDouble();
out.writeDouble(Math.PI*radius*radius);
}
}
catch(EOFException e) {} // End of file reached (4)
catch(IOException e) {
System.out.println(e.getMessage());
}
finally {
try { in.close(); } catch(Exception e){}
try { out.close(); } catch(Exception e){}
}
}
}| 1 | We change the Scanner from the text version of this program to a
DataInputStream. |
| 2 | We change the PrintWriter to a DataOutputStream. |
| 3 | We make what appears to be the strange choice of changing the while
loop to an infinite loop. We do this because the easiest way to see if there’s
any more data in a binary file is to keep reading until an
EOFException is thrown. |
| 4 | When the EOFException is thrown, we do nothing to handle it because, in
this case, it’s just a signal to stop reading. |
20.5. Solution: A picture is worth 1,000 bytes
Now, we’ll give the solution to the problem posed at the beginning of
the chapter. First, let’s look at the class definition and main()
method.
import java.io.*;
public class BitmapCompression {
public static void main(String[] args) {
if(args.length != 2) (1)
System.out.println("Usage: java BitmapCompression (-c|-d) file");
else {
DataInputStream in = null;
try {
in = new DataInputStream(new FileInputStream(args[1])); (2)
if(args[0].equals("-c")) (3)
compress(in, args[1]);
else if(args[0].equals("-d"))
decompress(in, args[1]);
}
catch(FileNotFoundException e) { (4)
System.out.println("File not found: " + e.getMessage());
}
finally { try{ in.close(); } catch(Exception e){} } (5)
}
}| 1 | We first check that there are exactly two command-line arguments. Otherwise, our program will crash when we try to access invalid array locations. For the wrong number of arguments, we print a usage message. |
| 2 | If we have the right number of arguments, we open a DataInputStream
based on the file named passed as the second command-line parameter. |
| 3 | Then, we either compress or decompress the file depending on which switch was passed as the first command-line parameter. |
| 4 | The catch will deal with the FileNotFoundException by printing an
appropriate error message. |
| 5 | Note the usual finally where the file is closed, including the inner
try-catch blocks needed to safely close binary files. |
public static void compress(DataInputStream in, String file) {
DataOutputStream out = null;
try {
String compressed = file + ".compress";
out = new DataOutputStream(new FileOutputStream(compressed)); (1)
byte current = 0;
int count = 1;
try {
current = in.readByte(); (2)
while(true) {
byte temp = in.readByte(); (3)
if(temp == current && count < 127)
count++; (4)
else { (5)
out.writeByte(count);
out.writeByte(current);
count = 1;
current = temp;
}
}
}
catch(EOFException e) { // Last sequence of bytes (6)
out.writeByte(count);
out.writeByte(current);
}
}
catch(IOException e) { (7)
System.out.println("Compression failed: " + e.getMessage());
}
finally { try { out.close(); } catch(Exception e){} }
}| 1 | In the compress() method, we first open a new DataOutputStream for
a file named the same as the input file with .compress tacked on the
end. |
| 2 | We read in the first byte of data. |
| 3 | Then, we keep reading bytes of data from the input file. |
| 4 | As long as we keep seeing the same byte, we increment a counter. |
| 5 | When we run into a new byte (or when we reach the limit of 127 of the same consecutive byte), we write the count and the byte we’ve been reading and move on, resetting the counter. |
| 6 | When an EOFException is thrown, we’ve reached the end of the file.
Because of the way our code is structured, we’ll always have at least one byte
(and possibly a long sequence of matching bytes) that we haven’t yet written
to the file. Consequently, we have to write the counter and the current byte
to finish. |
| 7 | The method finishes
with the usual catch and finally blocks needed to catch errors and
safely close the output file. |
public static void decompress(DataInputStream in, String file) {
DataOutputStream out = null;
try {
String original = file.substring(0, file.lastIndexOf(".compress")); (1)
out = new DataOutputStream(new FileOutputStream(original)); (2)
while(true) {
int count = in.readByte(); (3)
byte temp = in.readByte();
for(int i = 0; i < count; i++)
out.writeByte(temp);
}
}
catch(EOFException e) {} // Input finished (4)
catch(IOException e) { (5)
System.out.println("Decompression failed: " + e.getMessage());
}
finally { try{ out.close(); } catch(Exception e){} }
}
}| 1 | The decompress() method is simpler than compress(). It begins
by finding the original name of the file by removing .compress. Note that
this code will crash if the file being decompressed doesn’t end with
.compress. |
| 2 | Then, we open a new DataOutputStream for a file with the original name
we’ve found. |
| 3 | Next, we read a counter, read a byte value, and write the byte value as many times as the count specifies. |
| 4 | As before, an EOFException signals the end of the input file. |
| 5 | An additional catch and finally deal with errors and close the output
file. |
20.6. Concurrency: File I/O
By now, you’ve seen threads behave in unpredictable ways because of the way they’re reading and writing to shared variables. Isn’t a file a shared resource as well? What happens when two threads try to access a file at the same time? If both threads are reading from the file, everything should work fine. If the threads are both writing or doing a combination of reading and writing, there can be problems.
As we mentioned in Section 20.3, file operations are OS dependent. Although Java tries to give a uniform interface, different system calls are happening at a low level. Consequently, the results may be different as well.
Consider the following program that spawns two threads that both print a
series of numbers to a file called concurrent.out. The first thread
prints the even numbers between 0 and 9,999 while the second thread
prints the odd ones.
import java.io.*;
public class ConcurrentFileAccess implements Runnable {
private boolean even;
public static void main(String args[]) {
Thread writer1 = new Thread(new ConcurrentFileAccess(true)); (1)
Thread writer2 = new Thread(new ConcurrentFileAccess(false));
writer1.start(); (2)
writer2.start();
}
public ConcurrentFileAccess(boolean even) {
this.even = even;
}
public void run() {
PrintWriter out = null;
int start = even ? 0 : 1; (3)
try {
out = new PrintWriter(new File("concurrent.out")); (4)
for(int i = start; i < 10000; i += 2) (5)
out.println(i);
}
catch (FileNotFoundException e) {
System.out.println("concurrent.out not found!");
}
finally { if(out != null) out.close(); } (6)
}
}| 1 | The code in this program should have few surprises. The main() method
creates two Thread objects from ConcurrentFileAccess objects,
each with a different value for its even field. |
| 2 | Then, the main()
method starts the threads running. |
| 3 | In each thread’s run() method, it first decides on a starting point of
0 or 1 depending on whether it’s supposed to be even or odd. Note the use of
the ternary operator. |
| 4 | Each thread opens the file concurrent.out. |
| 5 | Then, it starts printing out even or odd numbers, depending on its starting point. |
| 6 | Afterward, each thread closes the file and ends. |
What do you expect the file concurrent.out to look like after the
program’s completed? Run it several times, on Windows, Linux, and macOS
systems if you can. The file might contain runs switching back
and forth between even numbers and odd numbers, but it’s likely that many
numbers, often about half, will be missing.
Why are half the numbers getting lost? When you open a file for writing, it overwrites the contents of the file. Thus, entire sequences of numbers are getting saved and then lost. We can change this behavior by changing the line below.
out = new PrintWriter(new File("concurrent.out"));We replace it with the following.
out = new PrintWriter(new FileOutputStream("concurrent.out", true));The PrintWriter constructor that takes a File object actually calls another
constructor internally that builds an output stream object. Instead, we can
pass in a FileOutputStream object created with a second boolean parameter
set to true. Doing so creates a FileOutputStream stream (and consequently a
PrintWriter) whose output will be appended to the file instead of
overwriting it.
After this change, what does the file look like when we run the program?
Since we’re going to append to the file instead of overwriting, make sure that
you delete concurrent.out before running the program again. As usual, the
file might look different on different systems. The file probably contains long
runs of numbers from each thread. In fact, it’s possible to have the complete
output from one thread followed by the complete output from the other.
For performance reasons, file operations are usually done in batches.
Instead of writing each number to the file as the thread produces it,
output is usually stored in a buffer which is written as a whole. By calling
out.flush() after each out.println() call, we could flush
the buffer to the file after each number is generated. Doing so won’t
be as efficient, but it may give us some insight into how concurrent
writes on files work.
Using flushes, the output from the two threads should be thoroughly intermixed. On a Windows machine, if you copy the data from the file and sort it, it’s possible that you’ll see some numbers missing. This lost output is similar to situations where updates to variables were lost because they were overwritten by another thread. On the other hand, most Linux systems have better concurrent file writing and won’t lose any numbers. (Even on Linux, it’s possible for a number to be printed in the middle of another number, but no digits should be lost.)
Under ideal circumstances, no two threads or processes should be writing
to the same file. However, this situation is sometimes unavoidable, as
with a database program that must support concurrent writes for the sake
of speed. If you need to enforce file locking, you can prevent threads
within your own program from accessing a file concurrently by using
normal Java synchronization tools. If you expect other programs to
interact with the same files that your program will use, Java provides a
FileLock class which allows the user to lock up portions of a file. As
with everything file related, FileLock is dependent on the underlying
OS and might behave differently on different systems. Also, FileLock
is a tool from the Java Non-blocking I/O (NIO) library, which provides
many impressive features but views I/O in a significantly different way from
the file I/O operations discussed in this chapter.
20.7. Exercises
Conceptual Problems
-
What’s the difference between volatile and non-volatile memory? Which is usually associated with files and why?
-
What’s the difference between text and binary files? What are the pros and cons of using each?
-
We can define compression ratio to be the size of the uncompressed data in bytes divided by the size of the compressed data in bytes. What’s the theoretical maximum compression ratio you could get out of the RLE encoding we used? What’s the theoretical lowest compression ratio you could get out of the RLE encoding we used?
-
What’s serialization in Java? What do you have to do to serialize an object?
Programming Practice
-
Write methods with the following signatures.
-
public static int readInt(FileInputStream in) -
public static long readLong(FileInputStream in) -
public static short readShort(FileInputStream in)
In each case, the method should read the appropriate number of bytes (4 for
int, 8 forlong, and 2 forshort) using theFileInputStreamobject and reassemble those bytes into the integer type specified. Your methods should be compatible with integers written by aDataOutputStreamobject. Note that such data is written in big-endian format. In other words, the first byte of data corresponds to the most significant byte in an integer, the second byte of data corresponds to the second-most significant byte, and so on. -
-
Program 20.5 from Example 20.3 computes the areas of circles whose radiuses are given as
doublevalues stored in a binary file. Although we provided a sample text file, we didn’t show a sample binary file since the contents would look like gibberish. Write a program that reads a file filled withdoublevalues stored as text and writes those same values into another file, storing thedoublevalues in binary. Afterward, you should be able to convert our sample text file into a sample binary file that can be used with Program 20.5. -
Re-implement the RLE bitmap compression program from Section 20.5 using only
FileInputStreamandFileOutputStreamfor file input and output. In some ways, doing so is simpler since you only needbyteinput and output for this program. -
Update the RLE bitmap compression program from Section 20.5 to use
JFileChooserto allow the user to select a file with a GUI instead of using command-line arguments. -
Re-implement the maze solving program from Section 19.5 to ask the user for a file instead of reading from standard input.
-
An HTML file contains many tags such as
<p>, which marks the beginning of a paragraph, and</p>, which marks the end of a paragraph. A lesser known feature of HTML is that ampersand (&) can mark special HTML entities used to produce symbols on a web page. For example,πis the entity for the Greek letter π. Because of these features of the language, raw text that’s going to be marked up in HTML should not contain less than signs (<), greater than signs (>), or ampersands (&).Write a program that reads in an input text file specified by the user and writes to an output text file also specified by the user. The output file should be exactly the same as the input file except that every occurrence of a less than sign should be replaced by
<, every occurrence of a greater than sign should be replaced by>, and every occurrence of an ampersand should be replaced by&. -
Write a program that prompts the user for an input text file. Open the file and read each word from the file, where a word is defined as any
Stringmade up only of upper- and lowercase letters. You can use thenext()method in theScannerclass to break up text by whitespace, but your code will still need to examine the input character by character, ending a word when any punctuation or other characters are reached. Store each word (with a count of the number of times you find it) in a binary search tree such as those described in Example 19.10. Then, traverse the tree, printing all the words found (and the number of times found) to the screen in alphabetical order. -
Expand the program from Exercise 20.12 so that it also prompts for a second file containing a dictionary in the form of a word list with one word on each line. Store the words from the dictionary in another binary search tree. Then, for each word in the larger document that you can’t find in the dictionary tree, add it to a third binary search tree. Finally, print out the contents of this third binary search tree to the screen, and you will have implemented a rudimentary spell checker. You can test the quality of your implementation by using a novel from Project Gutenberg and a dictionary file from an open-source spell checker or a Scrabble word list.
-
Files can become corrupted when they’re transferred over a network. It’s common to make a checksum, a short code generated using the entire contents of a file. The checksum can be generated before and after file transmission. If both of the checksums match, there’s a good chance that there were no transmission errors. Of course, there can be problems sending checksums, but checksums are much smaller and therefore less likely to be corrupted. Modern checksums are often generated using cryptographic hash functions, which are more complex than we want to deal with here. An older checksum algorithm works in the following way. Although we use mathematical notation, the operations specified below are integer modulus and integer division.
-
Add up the values of all the bytes, storing this sum in a
longvariable -
Set sum = sum mod 232
-
Let r = (sum mod 216) + (sum ÷ 216)
-
Let s = (r mod 216) + (r ÷ 216)
-
The final checksum is s
Remember that finding powers of 2 is easy with bitwise shifts. Write a program that opens a file for binary reading using
FileInputStreamand outputs the checksum described. On Linux systems, you can check the operation of your program with thesumutility, using the-soption. The following is an example of the command used on a file calledwombat.dat. The first number in the output below it,6892, is the checksum. -
sum -s wombat.dat 6892 213 wombat.dat
Experiments
-
Reading single bytes using either
FileInputStreamorDataInputStreamis slow. It’s much faster to read a block of bytes all at once. Re-implement the RLE bitmap compression program from Section 20.5 using theint read(byte[] b)method from theDataInputStreamclass, which tries to fill the arraybwith as manybytevalues as it can. If there are enough bytes left in the file, the array will be filled completely. If the array is longer than the remaining bytes, only the first part of the array will contain valid bytes. In either case, this method will return the number ofbytevalues successfully read into the array.Using a
bytearray of length 1,024, time the original program against the new version on files with sizes of about 500 KB, 1 MB, and 2 MB. There’s also avoid write(byte[] b, int off, int len)method inDataOutputStreamthat can write an entire array ofbytevalues at once. Using it for output would further increase the speed of your program at the price of greater complexity. -
Write the RLE bitmap compression program from Section 20.5 in parallel so that a file is evenly divided into as many pieces as you have threads, compressed, and then each compressed portion is output in the correct order. Compare the speed for 2, 4, and 8 threads to the sequential implementation. Are any of the threaded versions faster? Why or why not? Run some experiments to see how long it takes to read 1,000,000 bytes from a file compared to the time it takes to compress 1,000,000 bytes which are already stored in an array.
21. Network Communication
Arguing with anonymous strangers on the Internet is a sucker’s game because they almost always turn out to be—or to be indistinguishable from—self-righteous sixteen-year-olds possessing infinite amounts of free time.
21.1. Problem: Web server
It’s no accident that the previous chapter about file I/O is followed by this one about networking. At first glance, the two probably seem unrelated. As it happens, both files and networks are used for input and output, and the designers of Java were careful to create an API with a similar interface for both.
In the next two sections, we’ll discuss how this API works, but first we introduce the problem: You need to create a web server application. The term server is used to describe a computer on a network which other computers, called clients, connect to in order to access services or resources. When you browse the Internet, your computer is a client connecting to web servers all over the world. Writing a web server might seem like a daunting task. The web browser you run on your client computer, such as Microsoft Edge, Mozilla Firefox, Apple Safari, or Google Chrome, is a complicated program, capable of streaming audio and video, browsing in multiple tabs, automatically encrypting and decrypting secure information, and at the very least, correctly displaying web pages of every description.
In contrast, a web server application is much simpler. At its heart, a web server gets requests for files and sends those files over the network. More advanced servers can execute code and dynamically generate pages, and many web servers are multi-threaded to support heavy traffic. The web server you’ll write needs only to focus on getting requests for files and sending those files back to the requester.
21.1.1. HTTP requests
To receive requests, a web server uses something called hypertext
transfer protocol (HTTP), which is just a way of specifying the format
of the requests. The only request we’re interested in is the GET
request. All GET requests have the following format.
GET path HTTP/version
In this request, path is the path of the file being requested and version is
the HTTP version number. A typical request might be as follows.
GET /images/banner.jpg HTTP/1.1
You should also note that all HTTP commands end with two newline
characters ('\n'). The extra blank line makes it easier to separate
the commands from other data being sent.
21.1.2. HTTP responses
After your web server receives a GET message, it looks for the file
specified by the path. If the server finds the file, it sends the
following message.
HTTP/1.1 200 OK
Again, note that this message is followed with two newline characters. After this message is sent, the server sends the requested file, byte by byte, across the network. If the file can’t be found by the web server, it sends an error message as follows.
HTTP/1.1 404 Not Found
Of course, two newlines will be sent after this message as well. After the error message, servers will also typically send some default web page with an explanation in HTML.
Now, we return to the more fundamental problem of how to communicate over a network.
21.2. Concepts: TCP/IP communication
We begin where many discussions of computer networking begin, the Open Systems Interconnection Basic Reference Model (or OSI model). As we mentioned before, the designers of Java wanted to make a networking API which was very similar to the file system API. This single API is intended for JVMs running on Windows or on macOS or on Linux or any other operating system. Even with the same operating system, different computers have different hardware. Some computers have wired connections to a router or gateway. Others are connected wirelessly. Beyond your own computer, you have to figure out the address of the computer you want to send messages to and deal with its network, hardware, and software.
There are so many details in the process that it seems hopelessly complicated. To combat this problem, the OSI seven layer model was developed. Each layer defines a specification for one aspect of the communication path between two computers. As long as a particular layer interacts smoothly with the one above it and below it, that layer could take the form of many different hardware or software choices. Listing them in order from the highest level (closest to the user) to the lowest level (closest to the hardware), the layers are as follows.
-
Layer 7: Application Layer
-
Layer 6: Presentation Layer
-
Layer 5: Session Layer
-
Layer 4: Transport Layer
-
Layer 3: Network Layer
-
Layer 2: Data Link Layer
-
Layer 1: Physical Layer
The application layer is where your code is. The Java networking API calls that your code uses to send and receive data comprise the application layer for your purposes. The only thing above this layer is the user. Protocols like HTTP and FTP are the province of this layer. All the other communication problems have been solved, and the key issue is what to do with the data that’s communicated.
The presentation layer changes one kind of message encoding to another. This layer is not one people usually spend a lot of time worrying about, but some kinds of encryption and compression can happen here.
The session layer allows for the creation of sessions when communicating between computers. Sessions requiring authentication and permissions can be dealt with here, but in practice, this layer’s not often used. One notable exception is Transport Layer Security (TLS), the technology most commonly used to protect passwords and credit card numbers when you make online purchases.
The transport layer is concerned with the making the lower level communication of data more transparent to higher layers. This layer typically breaks larger messages into smaller packets of data which can be sent across the network. This layer can also provide reliability by checking to see if these packets make it to their destinations and resending them otherwise. The two most important protocols for this layer are Transmission Control Protocol (TCP) and User Datagram Protocol (UDP). For Internet traffic, TCP is more commonly used and provides reliable communication that ensures packets are delivered in order. TCP is used for file transfers, e-mail, web browsing, and any number of other web applications. UDP doesn’t have guarantees about reliability or ordering; however, UDP is faster. For this reason, UDP is used for streaming media and online games.
The network layer is responsible for packet transmission from source to destination. It’s concerned with addressing schemes and routing. The most well-known example of a network layer protocol is the Internet Protocol (IP) used to make the Internet work.
If the network layer worries about sending of packets from source to destination, the data link layer is responsible for the actual transmission of packets between each link in the chain. Here hardware becomes more important because there are so many different kinds of networks. Examples of data link layers include Ethernet, token ring networks, IEEE 802.11 Wi-Fi networks, and many more.
Finally, the lowest level is the physical layer. This layer defines the physical specifications for sending raw bits of information from one place to another, over a wire or wirelessly. This layer is typically the least interesting to programmers but is an important area for electrical engineers.
21.3. Syntax: Networking in Java
The seven layer model might seem overwhelming, but there are only a few key pieces we’ll need on a regular basis. In fact, the system of layers is designed to help people focus on the one or two layers specific to their needs and ignore the rest.
21.3.1. Addresses
The first topic we touch on is the network layer. What we need from this layer are addresses. A network address is much like a street address. It gives the location on the network of a computer so that messages can be sent there.
For most systems you use, such an address will be an IP address. There
are two current versions of IP addresses, IPv4 and IPv6. IPv6 is the way
of the future and provides a huge number of possible addresses. Not all
systems support IPv6, and the general public is often not aware of it.
Although it will one day be the standard, we use the more common IPv4
addresses here. An IPv4 address is typically written as four decimal
numbers separated by dots. Each of these four numbers is in the range 0-255.
For example, 64.233.187.99 and 192.168.1.1 are IPv4 addresses.
21.3.2. Sockets
The second topic we focus on is the transport layer. Here, you need to make a choice between TCP or UDP for communication. In this book, we only cover TCP communication because it’s reliable and more commonly used than UDP. If you need to use UDP communication, the basics are not too different from TCP, and there are many excellent resources online.
To create a TCP connection, you typically need a server program and a client program. The difference between the two is not necessarily big. In fact, both the client and the server could be running on the same computer. What distinguishes the server is that it sets up a port and listens on it, waiting for a connection. Once the client makes a connection to that port, the two programs can send and receive data on an equal footing.
We just mentioned the term port. As you know, an address is the location of a computer in a network, but a single computer might be performing many different kinds of network communications. For example, your computer could be running a web browser, an audio chat application, an online game, and a number of other things. So that none of these programs become confused and get each others' messages, each program uses a separate port for communication. To the outside world, your computer usually only has a single address but thousands of available ports. Many of these ports are set aside for specific purposes. For example, port 20 is for FTP, port 23 is for Telnet, and port 80 is for HTTP (web pages).
When you write a server program, you’ll usually create a
ServerSocket object linked to a particular port. For example,
if you wanted to write a web server, you might create a ServerSocket
as follows.
ServerSocket serverSocket = new ServerSocket(80);Once the ServerSocket object has been created, the server will
typically listen to the socket and try to accept incoming connections.
When a connection is accepted, a new Socket object is created for that
connection. The purpose of the ServerSocket is purely to set up this
Socket. The ServerSocket doesn’t do any real communication on its
own. This system might seem indirect, but it allows for greater
flexibility. For example, a server could have a thread whose only job is to
listen for connections. When a connection is made, it could spawn a new thread
to do the communication. Commercial web servers often function in this
way. The code for a server to listen for a connection is as follows.
Socket socket = serverSocket.accept();The accept() method is a blocking method; thus, the server will wait
for a connection before doing anything else.
Now, if you want to write the client which connects to such a server,
you can create the Socket object directly.
Socket socket = new Socket("64.233.187.99", 80);The first parameter is a String specifying the address of the server,
either as an IP address as shown or as a domain like "google.com". The
second parameter is the port you want to connect on.
Note that the Socket and ServerSocket classes are both in the java.net
package, so you’ll need to import java.net.* to use them and the rest of the
basic networking library.
21.3.3. Receiving and sending data
From here on out, we no longer have to worry about the differences
between the client and server. Both programs have a Socket object that
can be used for communication.
In order to get input from a Socket, you first call its
getInputStream() method. You can use the InputStream returned to
create an object used for normal file input like in
Chapter 20. You will need to make similar considerations
about the kind of data you want to read and write. If you only need to receive
plain, human-readable text from the Socket, you can create a Scanner
object as follows.
Scanner in = new Scanner(socket.getInputStream());Over the network, it will be more common to send files and other binary data.
For that purpose, you can create a DataInputStream or an ObjectInputStream
object from the Socket in much the same way.
DataInputStream in = new DataInputStream(socket.getInputStream());It should be unsurprising that output is just as simple as input. Text
output can be accomplished by creating a PrintWriter.
PrintWriter out = new PrintWriter(socket.getOutputStream());Likewise, binary output can be accomplished by creating an
ObjectOutputStream or a DataOutputStream.
DataOutputStream out = new DataOutputStream(socket.getOutputStream());Once you have these input and output objects, you use them in the same
way you would for file processing. There are a few minor differences to
keep in mind. In the first place, when reading data, you might not know
when more is coming. There’s no explicit end of file. Also, it’s
sometimes necessary to call a flush() method after doing a write.
A socket might wait for a sizable chunk of data to be accumulated before it
gets sent across the network. Without a flush(), the data you write might
not be sent immediately.
Here’s an example of a piece of server code which listens on port 4321,
waits for a connection, reads 100 int values in binary form from
the socket, and prints their sum.
try{
ServerSocket serverSocket = new ServerSocket(4321);
Socket socket = serverSocket.accept();
DataInputStream in = new DataInputStream(socket.getInputStream());
int sum = 0;
for(int i = 0; i < 100; i++)
sum += in.readInt();
in.close();
System.out.println("Sum: " + sum);
}
catch(IOException e) {
System.out.println("Network error: " + e.getMessage());
}Now, here’s a companion piece of client code which connects to port 4321
and sends 100 int values in binary form, specifically the first 100
perfect squares.
try{
Socket socket = new Socket("127.0.0.1", 4321);
DataOutputStream out = new DataOutputStream(socket.getOutputStream());
for(int i = 1; i <= 100; i++)
out.writeInt(i*i);
out.close();
}
catch(IOException e) {
System.out.println("Network error: " + e.getMessage());
}Note that this client code connects to the IP address 127.0.0.1. This
is a special loopback IP address. When you connect to this IP address,
it connects to the machine you’re currently working on. In this way,
you can test your networking code without needing two separate
computers. To test this client and server code together, you will
need to run two virtual machines. The simplest way to do so is to open
two command line prompts and run the client from one and the server from
the other. Be sure that you start the server first so that the client
has something to connect to. IDEs like Eclipse and IntelliJ will also allow
you to start two programs simultaneously, but it can be difficult to be certain
which one is which.
Here we look at a more complicated example of network communication, a chat program. If you want to apply the GUI design from Chapter 15, you can make a windowed version of this chat program which looks more like typical chat programs. For now, our chat program is text only.
The functionality of the program is simple. Once connected to a single
other chat program, the user will enter his or her name, then enter
lines of text each followed by a newline. The program will insert the
user’s name at the beginning of each line of text and then send it
across the network to the other chat program, which will display it. We
encapsulate both client and server functionality in a class called
Chat.
import java.io.*; (1)
import java.net.*;
import java.util.*;
public class Chat {
private Socket socket;
public static void main(String[] args) {
if(args[0].equals("-s")) (2)
new Chat(Integer.parseInt(args[1]));
else if(args[0].equals("-c")) (3)
new Chat(args[1], Integer.parseInt(args[2]) );
else
System.out.println("Invalid command line flag.");
}| 1 | The first step is the appropriate import statements. |
| 2 | In the main() method, if the first command-line argument is "-s", the
server version of the Chat constructor will be called. We convert the next
argument to an int and use it as a port number. |
| 3 | If the argument "-c" is given, the client version of the Chat
constructor will be called. We use the next two command-line arguments for the
IP address and the port number, respectively. |
// Server
public Chat(int port) {
try {
ServerSocket serverSocket = new ServerSocket(port); (1)
socket = serverSocket.accept();
runChat(); (2)
}
catch(IOException e) {
System.out.println("Network error: " + e.getMessage());
}
}| 1 | The server Chat constructor takes the port and listens for a
connection on it. |
| 2 | After a connection, it calls the runChat() method to
perform the actual business of sending and receiving chats. |
// Client
public Chat(String address, int port) {
try {
socket = new Socket(address, port);
runChat();
}
catch(IOException e) {
System.out.println("Network error: " + e.getMessage());
}
}The client constructor is similar but connects directly to the specified IP address on the specified port.
public void runChat() {
Sender sender = new Sender(); (1)
Receiver receiver = new Receiver();
sender.start(); (2)
receiver.start();
try {
sender.join();
receiver.join();
}
catch(InterruptedException e) {}
}| 1 | Once the client and server are connected, they both run the runChat()
method, which creates a new Sender and a new Receiver to do the
sending and receiving. |
| 2 | Note that both start() and join() are called
on the Sender and Receiver objects. These calls are needed because
both classes are subclasses of Thread. |
Sending messages is an independent task concerned with reading input from the keyboard and then sending it across the network. Receiving messages is also an independent task, but it’s concerned with reading input from the network and printing it on the screen. Since both tasks are independent, it’s reasonable to allocate a separate thread to each.
Below is the private inner class Sender. In this case it’s convenient
but not necessary to make Sender an inner class, especially since it’s
so short. The only piece of data Sender shares with Chat is the
all important socket variable.
private class Sender extends Thread {
public void run() {
try {
PrintWriter netOut = new PrintWriter(socket.getOutputStream()); (1)
Scanner in = new Scanner(System.in);
System.out.print("Enter your name: ");
String name = in.nextLine(); (2)
while(!socket.isClosed()) {
String line = in.nextLine(); (3)
if(line.equals("quit")) (4)
socket.close();
else {
netOut.println(name + ": " + line); (5)
netOut.flush();
}
}
}
catch(IOException e) {
System.out.println("Network error: " + e.getMessage());
}
}
} | 1 | The Sender begins by creating a
PrintWriter object from the Socket output stream. |
| 2 | It reads a name from the user. |
| 3 | Then, it waits for a line from the user. |
| 4 | If the user types quit, the Socket will be closed. |
| 5 | Otherwise, each time a line is read, it’s printed and flushed through the
PrintWriter connected to the Socket output stream, with the user name
inserted at the beginning. |
Below is the private inner class Receiver, the simpler counterpart of
Sender.
private class Receiver extends Thread {
public void run() {
try{
Scanner netIn = new Scanner(socket.getInputStream()); (1)
while(!socket.isClosed())
if(netIn.hasNextLine())
System.out.println(netIn.nextLine()); (2)
}
catch(IOException e) {
System.out.println("Network error: " + e.getMessage());
}
}
}| 1 | First, it creates a Scanner object connected to the input stream of the Socket. |
| 2 | Then, waits for a line of text to arrive from the connection. Each time a line arrives, it prints it to the screen. |
You can see that this problem is solved with threads much more
easily than without them. Both the in.nextLine() method called by Sender
and the netIn.nextLine() method called by Receiver are blocking calls.
Because each must wait for input before continuing, they can’t easily be
combined in one thread of execution.
Although the fundamentals are present in this example, a real chat
client should provide a contact list, the opportunity to talk to more than
one other user at a time, better error-handling code in the
catch-blocks, and many other features. Some of these features are
easier to provide in a GUI.
In the next section, we give a solution for the web server problem. Since only the server side is needed, some of the networking is simpler, and there are no threads. However, the communication is done in both binary and text mode.
21.4. Solution: Web server
Here’s our solution to the web server problem. As usual, our solution
doesn’t provide all the error checking or features that a real web
server would, but it’s entirely functional. When you compile and run
the code, it will start a web server on port 80 in the directory you run it
from. Feel free to change those settings in the main() method or create a
WebServer object from another program. When the server’s running, you should
be able to open any web browser and go to http://127.0.0.1. If you put
some sample HTML and image files in the directory you run the server from, you
should be able to browse them.
import java.io.*; (1)
import java.net.*;
import java.util.*;
public class WebServer {
private int port; (2)
private String webRoot;
public WebServer(int port, String webRoot) {
this.port = port;
this.webRoot = webRoot;
}
public static void main(String[] args) {
WebServer server = new WebServer(80, new File(".").getAbsolutePath()); (3)
server.start();
}| 1 | Our code starts with the necessary imports. |
| 2 | The server has fields for the port where communication will take place and the root directory for the web page. |
| 3 | The main() method calls the constructor using port 80 and a path
corresponding to the current directory (.) as arguments. Then, it starts
the server. |
Below is the start() method. This method contains the central loop of
the web server that waits for connections and loops forever.
public void start() {
Socket socket = null;
Scanner in = null;
DataOutputStream out = null;
String line;
try {
ServerSocket serverSocket = new ServerSocket(port); (1)
while(true) {
socket = serverSocket.accept();
try {
in = new Scanner(socket.getInputStream()) ; (2)
out = new DataOutputStream(socket.getOutputStream());
boolean requestRead = false;
while(in.hasNextLine() && !requestRead) { (3)
line = in.nextLine();
if(line.startsWith("GET")) {
String path = line.substring(4, (4)
line.lastIndexOf("HTTP")).trim();
System.out.println("Received request for: " + path);
serve(out, getPath(path)); (5)
socket.close(); (6)
requestRead = true;
}
}
}
catch(IOException e) { (7)
System.out.println("Error: " + e.getMessage());
}
}
}
catch(IOException e) {
System.out.println("Error: " + e.getMessage());
}
} | 1 | First, we create a ServerSocket to listen on the port. |
| 2 | Once a connection has been made, the server creates input and output objects from the socket connection. Then, it tries to serve requests coming from the socket input. |
| 3 | Our web server keeps reading lines until it finds a GET request. |
| 4 | When a GET request is made, the server removes the "GET " at the
beginning of the request and the HTTP version information at the end. |
| 5 | It passes the remaining file path to the serve() method. |
| 6 | Afterward, it closes the connection and sets requestRead to true so that
we stop looping through requests made on this particular connection to the
server. |
| 7 | All that remains in the start() method is the necessary exception handling
machinery. |
Note that the out object is of type DataOutputStream, allowing us
to send binary data over the socket. However, the in variable is of
type Scanner, because HTTP requests are text only.
Next is a short utility method which provides some amount of platform
independence. The getPath() method takes in a String representation
of a path requested by a web browser and formats it. This path should
always be given in the Unix or Linux style with slashes (/) separating
each directory.
public String getPath(String path) {
if('/' != File.separatorChar) (1)
path = path.replace('/', File.separatorChar);
if(path.endsWith("" + File.separatorChar))
return webRoot + path + "index.html"; (2)
else
return webRoot + path;
}| 1 | To function smoothly with other operating systems,
getPath() uses the class variable File.separatorChar which gives the
char used to separate directories on whichever platform the JVM is
currently running. |
| 2 | In addition, getPath() adds "index.html" to the
end of the path if the path is a directory rather than a file
name. Real web servers try a list of many different files such as
index.html, index.htm, index.php, and so on, until a file is found
or the list runs out. |
The last method in the WebServer class takes in a path and transmits the
corresponding file over the network.
public void serve(DataOutputStream out, String path) throws IOException {
System.out.println("Trying to serve " + path);
File file = new File(path);
if(!file.exists()) { (1)
out.writeBytes("HTTP/1.1 404 Not Found\n\n");
out.writeBytes("<html><head><title>404 Not Found</title></head>" +
"<body><h1>Not Found</h1>The requested URL " + path +
" was not found on this server.</body></html>");
System.out.println("File not found.");
}
else {
out.writeBytes("HTTP/1.1 200 OK\n\n"); (2)
DataInputStream in = null;
try {
in = new DataInputStream(new FileInputStream(file)); (3)
while(true)
out.writeByte(in.readByte()); (4)
}
catch(EOFException e) {
System.out.println("Request succeeded.");
}
catch (IOException e) {
System.out.println("Error sending file: " + e.getMessage());
}
finally { try{ in.close(); } catch(Exception e) {} } (5)
}
}
} | 1 | The serve() method first checks to see if the specified file exists. If
it doesn’t, the method sends an HTTP 404 response with a short explanatory
piece of HTML. Anyone who’s spent any time on the Internet should be familiar
with 404 messages. |
| 2 | On the other hand, if the file exists, the method sends an HTTP 200
response indicating success. |
| 3 | Then, it creates a new DataInputStream object to read the file. In this
case, it’s necessary to read the file in binary. In general, HTML files are
human-readable text files, but the image files that web servers must often send
such as GIF and JPEG files are binary files filled with unprintable characters.
Because we need to send binary data, we were also careful to open a
DataOutputStream on the socket earlier. |
| 4 | Once the file’s open, the serve() method simply reads it in, byte by
byte, and sends each byte out over the socket. It would be more efficient to
read a block of bytes and send them together, but our approach is simpler. |
| 5 | After the file has been sent, the method closes the DataInputStream and
returns. |
Because a web server is a real world application, we must repeat the caveat that this implementation is quite bare bones. There are other HTTP requests and many features, including error handling, that a web server should do better. Feel free to extend the functionality.
You might also notice that there’s no way to stop the web server. It
has an infinite loop that’s broken only if an IOException is thrown.
From a Windows, Linux, or macOS command prompt, you can usually stop a
running program by typing Ctrl+C.
21.5. Concurrency: Networking
Throughout this book, we’ve used concurrency primarily for the purpose of speedup. For that kind of performance improvement, concurrency is often icing on the cake. Unless you’re performing massively parallel computations such as code breaking or scientific computing, concurrency will probably make your application run just a little faster or a little smoother.
With network programming, the situation is different. Many networked programs, including chat clients, web servers, and peer-to-peer file sharing software, can be simultaneously connected to tens if not hundreds of other computers at the same time. While there are single-threaded strategies to handle these scenarios, it’s natural to handle them in a multi-threaded way.
A web server at Google, for example, might service thousands of requests per second. If each request had to wait for the previous one to come to completion, the server would become hopelessly bogged down. By using a single thread to listen to requests and then spawn worker threads as needed, the server can run more smoothly.
Even in Example 21.2, it was convenient to
create two different threads, Sender and Receiver. We didn’t create
them for speedup but simply because they were doing two different jobs.
Since the Sender waits for the user to type a line and the Receiver
waits for a line of text to arrive over the network, it would be
difficult to write a single thread that could handle both jobs. Both
threads call the nextLine() method, which blocks execution. A
single thread waiting to see if the user had entered more text could not
respond to text arriving over the network until the user hit enter.
We only touch briefly on networking in this book. As the Internet evolves, standards and APIs evolve as well. Some libraries can create and manage threads transparently, without the user worrying about the details. In other cases, your program must explicitly use multiple threads to solve the networking problem effectively.
21.6. Exercises
Conceptual Problems
-
Why are there so many similarities between the network I/O and the file I/O APIs in Java?
-
Explain the difference between client and server computers in network communication. Is it possible for a single computer to be both a client and a server?
-
Why is writing a web browser so much more complicated than writing a web server?
-
Name and briefly describe the seven layers of the OSI model.
-
Modern computers often have many programs running that are all in communication over a network. Since a computer often has only one IP address that the outside world can send to, how are messages that arrive at the computer connected to the right program?
-
What are the most popular choices of protocols at the transport layer of the OSI model? What are the advantages and disadvantages of each?
-
How many possible IP addresses are there in IPv4? IPv6 addresses are often written as eight groups of four hexadecimal digits, totaling 32 hexadecimal digits. How many possible IP addresses are there in IPv6?
Programming Practice
-
In Example 21.1 a client sends 100
intvalues, and a server sums them. Rewrite these fragments to send and receive theintvalues in text rather than binary format. You will need to send whitespace between the values. -
Add a GUI based on
JFramefor the chat program given in Example 21.2. Use a (non-editable)JTextAreato display the log of messages, including user name. Provide aJTextFieldfor entering messages, aJButtonfor sending messages, and anotherJButtonfor closing the network connections and ending the program. -
Study the web server implementation from Section 21.4. Implement a similar web server which is multi-threaded. Instead of serving each request with the same thread that is listening for connections, spawn a new thread to handle the request each time a connection is made.
-
One of the weaknesses of the web server from the previous exercise is that a new thread has to be created for each connection. An alternative approach is to create a pool of threads to handle requests. Then, when a new request arrives, an idle thread is selected from the pool. Extend the solution to the previous exercise to use a fixed pool of 10 worker threads.
Experiments
-
The web server program given in Section 21.4 sends files byte by byte. It would be much more efficient to send files in blocks of bytes instead of singly. Re-implement this program to send blocks of 1,024 bytes at a time. Time the difference it takes to send image files with sizes of about 500 KB, 1 MB, and 2 MB using the two different programs. If you can, also measure the time when you’re sending to a different computer, perhaps in the same computer lab. To do so, the person on the other computer will need to enter the IP address of your computer instead of
127.0.0.1. It would also be valuable to time how long it takes to send a file to a computer at a remote location, but doing so often involves changes to firewall settings to allow an outside computer to connect to your server. -
Consider the multi-threaded implementation of a web server from Exercise 21.10. Can you design an experiment to measure the average amount of time a client waits to receive the requested file? How does this time change from the single-threaded to the multi-threaded version? If the file size is larger, is the increase in the waiting time the same in both the single- and multi-threaded versions?